Paper1-scGAC 图注意力机制

Paper1 : scGAC 图注意力机制

1. 构建细胞图，NE去噪声

2. 图注意力自编码器学习聚类Embedding

3. 自由化的方式成簇

Introduction

p1（大背景

单细胞测序技术飞速发展，无监督聚类有效迫切需要

p2（局限性

尽管现有方法在进步，但由于稀疏高维，数据不稳定，细胞间的关系很难捕获

p3（现状1

针对高维问题，一般是用传统聚类来学习聚类的低维表示，Kmeans或者层次聚类。构造细胞-细胞相似矩阵来降低维数，欧氏距离只测量细胞间的线性相似度，很难捕捉到潜在的关系。

p4（现状2

RCSL：测量细胞之间的全局和局部关系，构建相似矩阵，然后从该相似矩阵推导出块对角矩阵，得到最终的聚类结果.

SC3: 基于不同相似度量和降维方法构建的多个相似矩阵的Kmeans,然后，将多个结果组合成一个共识矩阵，并对其进行层次聚类.

SAME: 集成了5种方法，为了得到更好的结果。

虽然这些方法明确地将细胞-细胞的相似度信息纳入到细胞的表示中，但成对的相似度只能表征细胞之间表面的而不是潜在的关系。而且，表征学习和聚类在这些方法中大多是两个独立的部分，不能相互受益，从而导致聚类结果不佳 representation learning and clustering是独立的

p5（动机1

为了同时学习特征表示和进行聚类，一些作品探索了两种基于深度学习的方法的结合:自动编码器和深度嵌入聚类(DEC) 自动编码器是目前最流行的深度框架之一，它可以以无监督的方式自动学习数据的低维表示。scDeepCluster 使用基于零膨胀负二项模型的自编码器对scRNA-seq数据的统计特征进行建模，并同时通过dec进行聚类。类似地，DESC预先训练一个堆叠的自编码器;然后，对编码器和DEC进行训练。通常，这些方法将表示学习和聚类结合到一个统一的框架中，以提高聚类性能。但是，它们在表示学习过程中只考虑基因表达信息，没有明确刻画细胞之间的关系。因此，习得的细胞表示不够聚类友好。

p6（动机2

为了将表达信息和关系信息自然嵌入潜在表示中，最近开发的一种方法scGNN 将新兴的图卷积网络结合到单细胞聚类中。GCN通过邻居信息传播学习图中节点的表示，同时考虑到节点特征和图拓扑。已经证明，通过GCN学习的表示可以改善聚类结果。scGNN将GCN集成到它的多自编码器框架中。首先利用特征自编码器构造GCN的细胞图;然后，通过基于gcn的自编码器学习图中细胞的表示，并对细胞表示进行k-means运算得到聚类结果。同一集群中的单元格表示由一些集群自动编码器迭代调整。但是，由于构建的图可能包含一些连接不同类型细胞的噪声边，而基于gcn的自编码器直接在相邻细胞之间传播信息而不区分它们，不同的细胞类型可能会混淆，从而误导聚类结果。

p7（工作解决了哪些问题

提出了单细胞图注意聚类,首先构造一个单元图，每个节点代表一个单元，每条边连接一个单元，权重由皮尔逊相关系数初始化。为了提高单元图的可信度，对单元图进行网络去噪，去除噪声边缘。基于去噪后的细胞图，scGAC通过图注意自编码器学习细胞的潜在表征，利用基因表达和细胞-细胞关系信息。注意机制有助于scGAC在跨邻域传播信息时为不同的邻域分配不同的权重。为了同时学习表示和优化聚类，采用自优化方法得到聚类结果。在16个真实scRNA-seq数据集上的实验表明，scGAC具有良好的聚类性能，优于现有的单细胞聚类方法。

Summary1

传统聚类方法构建相似度信息来学习细胞的表示，无法呈现细胞的潜在关系。representation learning and clustering是独立的。所以需要深度学习，但是深度学习学到的表征不是聚类友好的，所以用图深度聚类. 但是GCN直接在相邻细胞之间传播信息，不区分，所以引入注意力机制来学习潜在表征。

Materials and methods

p1（scGAC的架构

原始计数基因表达矩阵$R_{m\ast n}$，m个基因，n个细胞。数据清洗后归一化变成$X_{m\ast n}$。主要架构包括三个部分：

• 图的构建：在$X_{m\ast n}$的基础上，计算皮尔逊相关系数得到$S_{n\ast n}$ 然后进行网络增强去除噪声，每个细胞和它的k近邻都在去噪后的矩阵$E_{n\ast n}$上，用边连接起来形成$A_{n\ast n}$
• 图注意力编码器：图注意力自动编码器学习细胞嵌入$Z_{d\ast n}$，通过聚合具有不同权重的邻居特征，其中d表示自编码器的bottleneck层大小。它分为两部分，特征矩阵$Y_{D\ast n}$和辅助图$A_{n\ast n}$作为输入，输出一个重构矩阵$Y_{D\ast n}^{\prime }$。特征矩阵$Y_{D\ast n}$是从$X_{m\ast n}$变换而来, D为特征维数。$Y_{D\ast n}^{\prime }$和$Y_{D\ast n}$之间的平均绝对误差(MAE)来监督学习过程。
• 自优化聚类：给定簇数c，隶属矩阵$Q_{c\ast n}$来表征一个cell属于cluster的概率，更新聚类中心，提供聚类结果。然后，优化矩阵$P_{c\ast n}$被构造为$Q_{c\ast n}$的目标。$Q_{c\ast n}$和$P_{c\ast n}$之间的KL散度被用来计算和调整细胞嵌入，提高聚类结果。

p2（网络去噪

为了在相似的单元间共享信息并学习更友好的聚类单元嵌入，图注意自动编码器需要一个细胞图。由于scRNA-seq数据中细胞之间没有直接关系，因此需要构造一个可信赖的辅助图。

首先计算Pearson相关系数来度量细胞之间的相似度，并构造初始相似矩阵$S_{n\ast n}$。然而，由于scRNA-seq数据是噪声和高维的，细胞之间的相似性可能被错误估计。不正确的相似度会严重误导信息共享过程和聚类结果。

这里我们采用NE去噪$S_{n\ast n}$。给定一个加权图，eigengap是两个连续特征值之差，最稳定的聚类通常由最大化eigengap的值k给出。NE可以增加eigengap, 同时保留其邻接矩阵的特征向量，从而更好地检测聚类。这样一来，连接不同单元格的边的权值就会被削弱。

具体来说，我们执行NE将$S_{n\ast n}$转化为重新计算权重的相似性矩阵$E_{n\ast n}$，$E_{n\ast n}$的计算过程如下：
$$E_{ij}=\{\begin{array}{ll}{S}_{ij}& \text{ if }{\hat{E}}_{ij}\ge t\\ 0& \text{ otherwise }\end{array},\text{\hspace{1em}(1)}$$
其中t为预先定义的阈值。如果Eij过小(小于t)，则将Sij视为噪声，将Eij设为零。

对于每个单元格，我们根据$E_{n\ast n}$选择K个最相似的单元格作为它的邻居。每一对邻居将由$A_{n\ast n}$中的一条边连接。

p3（图注意力自动编码器

受到ICLR2018的工作启发，我们设计了一种图注意自动编码器，它由一个包含两个堆叠的图注意层的编码器和一个结构对称的解码器组成，将拓扑信息嵌入到细胞的潜在表示中。给定一个单元图，图注意层通过聚合具有不同权重的相邻单元的特征来学习单元的特征。由于权重是根据细胞及其邻居的特征自动分配的，因此可以自然地捕获潜在的关系。因此，学习到的特征可以更有利于集群。

图注意层可被表示为：
$${\mathbf{h}}_i^{\prime }=\sigma \left(\sum _{j\in N_i}{\alpha }_{ij}{\mathbf{W}\mathbf{h}}_j\right)\text{\hspace{1em}(2)}$$
这里${\mathbf{h}}_i^{\prime }$是细胞i的新特征，$N_i$是细胞i的邻居集合，$h_j$是细胞j的输入特征，W是一个可学习的变换矩阵。$\sigma$是一个非线性激活函数。${\alpha }_{ij}$为权重系数，表示单元j对单元i的重要性。

为了测量一个细胞对另一个细胞的重要性，最初的GAT将它们的特征拼接，得到注意系数$e_{ij}$，可表示为:
$$e_{ij}=\mathrm{LeakyReLU}\left({\mathbf{a}}^T\left[\mathbf{W}{\mathbf{h}}_i||\mathbf{W}{\mathbf{h}}_j\right]\right)\text{\hspace{1em}(3)}$$
其中LeakyReLU是一个非线性函数，$\alpha$是一个可学习权向量，||是拼接操作。

与GAT不同的是，我们将相似度信息显式地整合到注意系数中，注意系数通过高斯核变换两个单元间的距离来计算:
$$e_{ij}=\exp \left(-{\left|{\mathbf{a}}_1^T\mathbf{W}{\mathbf{h}}_i-{\mathbf{a}}_2^T\mathbf{W}{\mathbf{h}}_j\right|}^2\right)\text{\hspace{1em}(4)}$$
其中$\alpha 1$和$\alpha 2$分别是细胞i和细胞j的可学习权向量。

一般情况下，注意系数会通过一个softmax函数进行归一化，使其在不同单元间具有可比性，表示为:
$${\alpha }_{ij}=\mathrm{softmax}\left(e_{ij}\right)=\frac{\exp \left(e_{ij}\right)}{{\sum }_{k\in N_i}\exp \left(e_{ik}\right)}\text{\hspace{1em}(5)}$$
与GAT类似，我们采用多头注意力来稳定学习过程。使用G个独立注意模块共同学习表示，可表述为:
$${\mathbf{h}}_i^{\prime }=\underset{g=1}{\overset{G}{⨁}}\sigma \left(\sum _{i\in N_i}{\alpha }_{ij}^g{\mathbf{W}}^g{\mathbf{h}}_j\right)\text{\hspace{1em}(6)}$$
这里$⨁$是一个聚合操作。对自编码器的前三层和最后一层分别使用拼接函数和平均函数作为聚合运算。

在实施中，$Y_{D\ast n}$和$A_{n\ast n}$被输入到图注意自编码器中，分别提供基因级表达信息和细胞级拓扑信息。为了约束学习过程，计算重构特征矩阵$Y_{D\ast n}^{\prime }$和原始输入矩阵$Y_{D\ast n}$的MAE为重建损失:
$$L_r=\sum _{i=1}^D\sum _{j=1}^n\left|Y_{ij}-Y_{ij}^{\prime }\right|\text{\hspace{1em}(7)}$$

p4（自优化聚类

在预先训练图注意自编码器后，潜在表示矩阵$Z_{d\ast n}$，可以从细胞与细胞的关系和基因表达两个方面表征细胞。通过执行k-means可以获得一个简单聚类结果 。然而，这个结果可能是次优的，因为聚类模块不与特征学习模块交互。因此，我们采用迭代自优化的聚类方法，让两个模块相互受益，最终提高结果。

首先，基于学生的t分布(如DEC中所采用的方法)，我们测量细胞和簇中心之间的相似性。在细胞层面归一化后，一个隶属矩阵$Q_{c\ast n}$，可计算为:
$$q_{ij}=\frac{{\left(1+{\Vert {\mathbf{z}}_i-{\mathbf{u}}_j\Vert }^2\right)}^{-1}}{{\sum }_{k=1}^c{\left(1+{\Vert {\mathbf{z}}_i-{\mathbf{u}}_k\Vert }^2\right)}^{-1}},\text{\hspace{1em}(8)}$$
其中$z_i$为细胞i的嵌入，$u_j$为聚类中心j的嵌入，c为细胞类型的数量。

然后，得到优化的隶属矩阵$P_{c\ast n}$，是根据$Q_{c\ast n}$构建的，定义为:
$$p_{ij}=\frac{q_{ij}^2/{\sum }_{i=1}^n{q}_{ij}}{{\sum }_{k=1}^c\left(q_{ik}^2/{\sum }_{i=1}^n{q}_{ik}\right)}\text{\hspace{1em}(9)}$$
它被用作$Q_{c\ast n}$，优化和重新分配成员。再分配后，由于平方运算，单元的隶属度分布更加确定。

此外，总隶属度较低的集群$\left({\sum }_{i=1}^n{q}_{ij}\right)$将获得相对较高的隶属度。然后根据$Q_{c\ast n}$和$P_{c\ast n}$，以获得更好的聚类结果。为了更好地表征聚类，采用细胞加权平均更新聚类中心的嵌入，采用$Q_{c\ast n}$为权重，计算公式为:

$${\mathbf{u}}_j=\frac{{\sum }_{l_i=j}{q}_{ij}{\mathbf{z}}_i}{{\sum }_{l_i=j}{q}_{ij}}\text{\hspace{1em}(10)}$$
其中$l_i$为本次迭代中细胞i的簇标签，定义为:
$$l_i=\arg \underset{i}{\max }{q}_{ij}\text{\hspace{1em}(11)}$$
另一方面，为了监督潜在表征的学习和增强底层聚类结构，$Q_{c\ast n}$和$P_{c\ast n}$间的散度被定义为聚类损失:
$$L_c=\sum _{i=1}^c\sum _{j=1}^n{p}_{ij}\log \frac{p_{ij}}{q_{ij}}\text{\hspace{1em}(12)}$$
在训练过程中，我们基于潜在表示计算轮廓分数，以监测早期停止的聚类性能。单元格i的轮廓分数计算为:
$$s_i=\frac{b_i-a_i}{\max \left(a_i,b_i\right)},\text{\hspace{1em}(13)}$$
其中$a_i$为细胞I与同一簇细胞之间的平均距离，$b_i$为细胞I与不同簇细胞之间的平均距离。聚类结果的轮廓分数是所有细胞的平均轮廓分数。细胞和簇中心的潜在表示将被迭代微调，直到轮廓分数收敛。

综上所述，总损失函数计算为:
$$L=L_{\mathrm{r}}+\gamma L_{\mathrm{c}}\text{\hspace{1em}(14)}$$
其中Lr为重构损耗，Lc为聚类损耗，$\gamma $为平衡两个损耗的超参数。损失函数将潜在表示学习和聚类整合到一个统一的框架中，从而促进最终的聚类结果。

p5（数据集和预处理

在16个真实数据集进行评估。All the original tested datasets (Yan, Biase, Klein, Romanov, Muraro, Björklund, PBMC, Zhang, Guo, Brown.1, Brown.2, Chung, Sun.1, Sun.2, Sun.3 and Habib) can be downloaded.

这些数据集的大小从几十到数千不等，来自不同的组织和平台。例如，数据集Biase只包含3种细胞类型的49个细胞，而数据集Habib包含10788个细胞，10种类型的小鼠细胞核。

聚类前，表达式矩阵$R_{m\ast n}$被预处理为$X_{m\ast n}$通过执行质量控制和标准化。首先，如果细胞的总读取计数或表达的基因数量超过上阈值或低于下阈值，则删除低质量的细胞。此外，在3个以下细胞中表达的低质量基因也被去除。经质量控制后，读数除以库大小，乘以100000,通过log2转换变成1的伪计数。

为了加速后续的学习过程，$X_{m\ast n}$降维为$Y_{D\ast n}$，然后输入到图形自动编码器。主成分分析(PCA)默认用于降维。

对于小数据集(n < D)，选择前D个高变量基因，因为PCA无法在它们上运行。$Y_{D\ast n}$归一化为z-score数据，均值和单位方差为零。

p6（基准构建

p6.1（参数设置

对于scGAC，用于图构造的默认邻居数计算为：
$$K=\mathrm{round}\left(\frac{N_{\text{cells }}}{10\times N_{\text{clusters }}}\right)\text{, }\text{\hspace{1em}(15)}$$
其中Ncells是细胞的数量，Nclusters是集群的数量。为了保证构建的图是有效可靠的，K被限制在6到20之间。我们将输入特征的维数D设为512。图注意自编码器由4个头部组成，每个头部包含一个两层编码器(第一层64个神经元，第二层16个神经元)和一个两层解码器(第一层64个神经元，第二层512个神经元)。损失系数c设为1。通过学习率为0.0002的Adam优化器对模型进行预训练，并以学习率为0.0005进行训练。

p6.2（baseline 方法

七种最先进的单细胞聚类方法，CIDR, SC3, SAME, RCSL, scDeepCluster, DESC和scGNN ，作为基线方法进行评估。

对于CIDR、SAME和scDeepCluster，为其后续的预处理和聚类提供原始数据。对于SAME算法，采用BIC准则产生的聚类结果作为其解。对于SC3，根据其要求提供原始数据和日志转换数据。对于DESC，按照其在线教程(https://eleozzr.github.io/desc/tutorial.html)进行归一化、日志转换、基因选择和缩放，并使用“分辨率”为0.8的聚类结果作为其解。对于scGNN，进行了数据预处理和LTMG推断。SC3和scDeepCluster提供了集群数量。所有方法的参数都设置为默认值或遵循教程。

p6.3（细胞embeddings的分析

对于基于深度学习的方法，包括scGAC, scDeepCluster, DESC和scGNN，在自编码器的瓶颈层中获得潜在表示作为细胞嵌入。对于CIDR，得到了不相似矩阵。对于RCSL，得到了块对角矩阵。对于SAME和SC3，由于没有合适的细胞嵌入，所以不进行嵌入分析。为了量化细胞嵌入的簇内纯度和簇间分化，根据标注的细胞类型标签计算轮廓系数评分。

为了可视化，当得到的嵌入维数超过50维时，PCA将其压缩到50维。接下来，通过t-分布式随机邻居嵌入(t-SNE) 将其进一步简化为2维进行演示。2D可视化平面中的点将根据其标注的单元格类型进行着色。

p6.4（评估指标

两个指标，调整兰德指数(ARI)和归一化互信息(NMI) ，用于评估scGAC和基线方法的聚类性能。

ARI度量聚类结果与ground truth的相似度，计算结果为:
$$\text{ ARI }=\frac{{\sum }_{ij}\left(\begin{array}{c}{n}_{ij}\\ 2\end{array}\right)-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_i\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{l}n\\ 2\end{array}\right)}{\frac{1}{2}\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right)+{\sum }_i\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_i\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{c}n\\ 2\end{array}\right)}\text{\hspace{1em}(16)}$$
其中，nij为ground truth中的聚类i和聚类结果中的聚类j之间共享的细胞数量，n为所有细胞的数量，$a_i={\sum }_j{n}_{ij}\text{ and }{b}_j={\sum }_i{n}_{ij}\text{. }$

NMI度量聚类结果与ground truth之间的归一化互信息，计算为:
$$NMI=\frac{2MI(U,V)}{H(U)+H(V)},\text{\hspace{1em}(17)}$$
其中U为聚类结果，V为基础真理，MI(U, V)表示U和V之间的互信息，H是熵函数。

为了公平比较，scGAC和基线方法重复运行10次，计算平均ARI和NMI进行评估。

Summary2

主要用了3个trick：NE，图注意力机制和自动优化聚类。再加上图深度聚类很少用于single cell中，所以论述的力度有效。

Result

p1（scGAC聚类性能对比

将scGAC应用于16个真实数据集，并与7种基线方法进行比较。总体而言，scGAC在ARI和NMI评分方面的表现都是最好的。在16个数据集中的9个在ARI评分方面优于所有基线方法。在其余7个数据集中，scGAC的表现也是第二好的。

此外，基于ARI和NMI得分(补充图S1和表S2)， scGAC在所有数据集上的平均得分最高。

p2（scGAC学到了聚类友好的 embedding

为了观察scGAC是否学习到更有利于聚类的细胞嵌入，我们获得了scGAC和5种基线方法的学习嵌入，并将其簇内纯度和簇间分化与基于轮廓系数的输入表达矩阵中细胞的原始特征进行了比较。

如图3所示，scGAC在16个评估数据集中有一半的轮廓系数最高，并且优于原始特征在几乎所有的数据集中。scGAC在所有数据集中拥有最高的平均轮廓得分，比第二好的方法DESC高出30.9%。结果表明，scGAC学习的细胞嵌入在不同的细胞类型中更容易区分，在同一细胞类型中具有高度的一致性。

值得注意的是，除了scGAC之外，在学习嵌入细胞的同时进行聚类的DESC和scDeepCluster两种方法也获得了平均第二和第三高的剪影分数。这意味着嵌入学习和聚类的交互作用有效地改善了数据的聚类特征。

此外，为了直观地观察潜在的表征，我们通过t-SNE可视化。如图3b所示，只有scGAC得到了4个边界非常清晰的纯聚类，这比其他方法要好得多。对于scGNN，这四个集群是纯的，但不明显。RCSL是将同一类型的细胞分开，而将不同类型的细胞(NK细胞和ILC3细胞)混合。对于CIDR、scDeepCluster和DESC，不同类型的细胞混合在一起。PBMC由四种免疫细胞组成，包括单核细胞、NK细胞、B细胞和T细胞，它们更容易聚集。如图3c所示，scGAC、scDeepCluster和DESC的可视化效果相对较好，CIDR将细胞混合在一起，RCSL和scGNN将NK细胞或B细胞分成子簇。用所有方法都很难将NK细胞从T细胞中分离出来。虽然scGAC只产生3个簇，NK细胞和T细胞紧密结合在一起，但scGAC中的NK细胞比scDeepCluster和DESC中的NK细胞纯度更高。

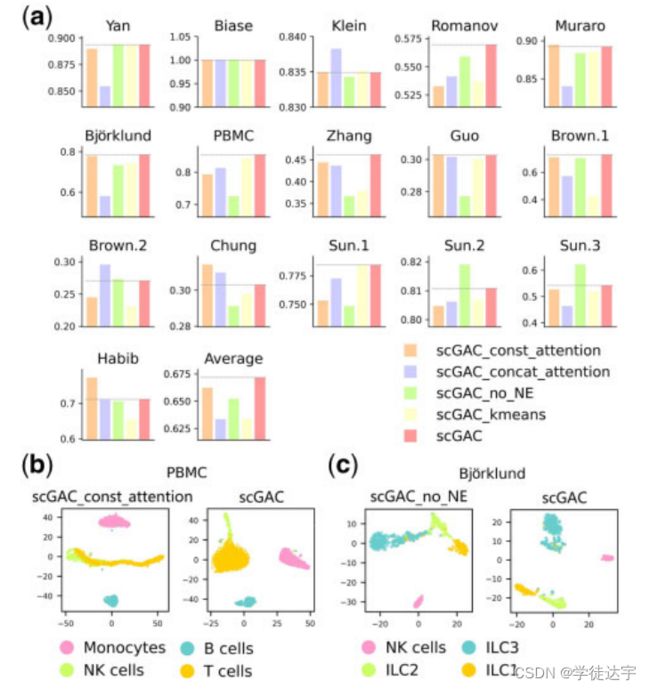
p3（图注意力编码器提升了聚类性能

为了获得更好的聚类结果，我们使用一个图注意自编码器来学习细胞的嵌入，同时利用细胞之间的拓扑关系。图注意自动编码器使图中的邻居之间能够灵活地共享信息，从而使嵌入更加集群友好。

为了探究scGAC中信息共享的效果，我们还运行scGAC，并将邻居的数量K设置为1，这意味着除了自己之外，没有一个单元可以将信息传递给另一个单元。补充表S3显示了scGAC在16个数据集上的ARI得分，K分别设为1 (scGAC_no_neighbor)和设为default (scGAC)。scGAC优于scGAC_no_neighbor，在大多数数据集上的ARI得分显著高于scGAC_no_neighbor，平均提高42.3%，这表明阻止信息共享严重阻碍了聚类。

因此，利用单元格之间的关系非常重要可以受益于集群。然而，值得注意的是，应该避免过度分享信息。在不同细胞类型的细胞之间共享特征信息会干扰聚类，因为不同细胞类型的特征会被遮蔽。

我们利用注意机制来缓解上述问题。由于在自动编码器中的图注意层，可以自动区分一个单元的不同邻居的重要性。

因此，一个单元可以有选择地从不同的邻居接收信息。为了评估注意机制的好处，我们还运行了持续注意scGAC (scGAC_const_attention)。所有的邻居将被分配到一个相同的常量权重，从而对特征学习过程做出相同的贡献。如图4a所示，在大多数数据集中，scGAC的ARI得分高于scGAC_const_attention。此外，scGAC在ARI平均得分上比scGAC_const_attention提高1.4%。

此外，为了直观地展示注意机制的重要性，我们将它们可视化地嵌入到数据集PBMC中。

如图4b所示，在没有注意机制的情况下，NK细胞和T细胞更难分离，说明没有选择的情况下接收所有信息可能会误导特征学习。

此外，注意力的实现机制也会影响聚类结果。与原有的GAT通过拼接操作实现注意机制不同，scGAC明确地将细胞间的相似信息集成到注意计算中，可以提高学习到的特征。

因此，我们还评估了连接注意机制(scGAC_concat_attention)进行比较。如图4a所示，在大多数数据集上，scGAC优于scGAC_concat_attention，平均ARI评分提高了6%。

因此，将相似信息整合到注意机制中确实有利于单细胞聚类。

p4（NE有益于构建细胞图

如前一节所述，跨单元的信息共享对于集群至关重要。它是否有益还取决于构建的单元图的可靠性，因为信息只会在图中连接的单元之间共享。因此，采用NE对单元图进行去噪和改进。

为了观察NE是否有利于构建单元格图，我们分别计算了在使用或不使用NE构建的单元格图中正确边(连接相同单元格类型的单元格)的比例(补充表S4)。比例越高，表示单元图的可靠性越高。在大多数数据集中，用网元去噪的单元图具有较高的正确边缘比例。对于简单的数据集，如数据集Yan和Biase，不同的单元类型非常不同，不使用NE构造的单元图是足够可靠的。然而，对于更复杂的数据集，不同的单元类型很难分离，NE带来了显著的改进。具体来说，NE为数据集Zhang带来了8.6%的改进，为数据集Bjo¨rklund带来了6.5%的改进，为数据集Guo带来了5.3%的改进。

此外，我们还应用了不引入NE的scGAC (scGAC_no_NE)对评价d、d、t、s、t进行评价。在图4a中，对于大多数数据集，特别是正确边比例提高较高的数据集(补充表S4)，如Bjo¨rklund、PBMC、Zhang和Guo数据集，有NE的scGAC获得的ARI得分显著高于无NE的scGAC。整体而言，NE促进scGAC在ARI平均评分上提高3%。

此外，为了直观地演示NE的有效性，我们分别可视化了使用和不使用NE学习的数据集Bjo¨rklund的细胞嵌入(图4c)。与没有NE的scGAC相比，在scGAC中ILCs可以清晰地分为三个簇，这意味着NE有效地去除了单元图中的噪声边缘。因此，NE确实有助于构建更可靠的单元图，提高聚类结果。

p5（自优化聚类模块提升了聚类性能

除了图注意自编码器，scGAC的另一个重要组成部分是自优化聚类模块，它为scGAC提供最终的聚类结果。它优化聚类中心并重新分配成员，使其更具确定性。同时，它还与图注意自动编码器相互作用，帮助更新学习到的嵌入。

为了验证自优化聚类模块是否改善了聚类结果，我们展示了图4a中自优化聚类前的聚类结果(scGAC_kmeans)，该聚类结果仅对预训练的嵌入执行k-means得到。与只有k-means的scGAC相比，scGAC在几乎所有数据集上都有更高的ARI得分，尤其是在自优化聚类前ARI得分较低的数据集，表明了自优化聚类的有效性。例如，自优化聚类后，Brown.1数据集的ARI评分提高了71.8%，Zhang数据集提高了21.8%，Brown.2数据集提高了17%。因此，k-means提供的聚类解是次优的，可以通过附加的自优化聚类模块进行改进。

Summary3

实验部分没有什么亮点，主要验证了2种所提出的3种trick的有效性，并且和第一段形成呼应，可以考虑加个时间对比。

Discussion

聚类是后续分析scRNA-seq数据的关键步骤。然而，聚类单细胞存在高维、高变量和高噪声数据的问题。在本文中，我们提出了一种新的单细胞聚类方法scGAC。scGAC通过注意机制在相似的细胞之间共享信息，学习聚类友好嵌入的细胞，并利用NE和自优化聚类提高聚类结果。

实验结果表明，scGAC在16个数据集上取得了优异的聚类性能，优于7种专门针对scRNA-seq数据设计的聚类方法。

此外，scGAC的不同成分已被证明对scGAC有显著和有益的作用。此外，scGAC在真实数据集上表现出良好的泛化能力，无论数据集的大小、单元类型的数量以及单元类型之间的差异。

scGAC的一个局限性是它的效率。scGAC在评估数据集上的运行效率中等，低于DESC、CIDR和SC3(补充表S5)。值得注意的是，其他考虑成对细胞-细胞关系的方法，如scGNN和RCSL，效率也很低，因为运行时间会随着细胞数量的增加而显著增加。因此，为了处理更大的数据集，我们将考虑在未来利用单元之间的关系的同时加速学习过程。
GAC在16个数据集上取得了优异的聚类性能，优于7种专门针对scRNA-seq数据设计的聚类方法。

此外，scGAC的不同成分已被证明对scGAC有显著和有益的作用。此外，scGAC在真实数据集上表现出良好的泛化能力，无论数据集的大小、单元类型的数量以及单元类型之间的差异。

scGAC的一个局限性是它的效率。scGAC在评估数据集上的运行效率中等，低于DESC、CIDR和SC3(补充表S5)。值得注意的是，其他考虑成对细胞-细胞关系的方法，如scGNN和RCSL，效率也很低，因为运行时间会随着细胞数量的增加而显著增加。因此，为了处理更大的数据集，我们将考虑在未来利用单元之间的关系的同时加速学习过程。