cs224w（图机器学习）2021冬季课程学习笔记11 Theory of Graph Neural Networks

诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

VX号“PolarisRisingWar”可直接搜索添加作者好友讨论。

更新日志：
2021.11.16 删除PPT链接，美化公式排版

YouTube 视频观看地址1 视频观看地址2

---

本章主要内容：
本章主要学习GNN模型的表达能力expressive power，即将不同图数据表示为不同嵌入向量的能力。
我们主要考虑图中节点的局部邻居结构 local neighborhood structure 信息，GNN通过计算图 computational graph 捕获节点的局部邻居结构。
因此，GNN无法区分具有相同计算图的节点。
如果GNN能将具有不同计算图的节点区分开来（即形成一个单射rejective函数，不同计算图的节点被表示为不同的嵌入），则我们称该GNN具有强表达能力，即计算图中的信息得到了完全的保留。要实现这样的区分度，需要GNN的聚合函数是单射的。

已知聚合函数表达能力越强，GNN表达能力越强，单射聚合函数的GNN表达能力最强。我们设计具有最强表达能力的GNN模型：
邻居聚合过程可被抽象为一个输入为multi-set的函数。
均值池化（GCN）无法区分各类占比相同的multi-set，最大池化（GraphSAGE）无法区分具有相同的不同类的multi-set，因此都不单射，不够具有表达能力。
为了建立在信息传递message-passing框架下的最强GNN，我们需要设计multi-set上的单射邻居聚合函数。根据Xu et al. ICLR 2019¹ 的定理，我们可以设计一个含 $\Phi$ 和 $f$ 两个未知函数、并应用sum-pooling的函数来表示这样的单射函数，根据universal approximation theorem² 可知 $\Phi$ 和 $f$ 可以通过MLP拟合得到。从而建立 Graph Isomorphism Network (GIN) 模型。
GIN是WL graph kernel³ 的神经网络版。GIN和WL graph kernel³ 都可以区分大部分真实图。

在表达能力上，sum（multiset） > mean（distribution）> max（set）

---

1. How Expressive are Graph Neural Networks?

1. 对GNN定义、聚合邻居信息思想的复习内容不赘。
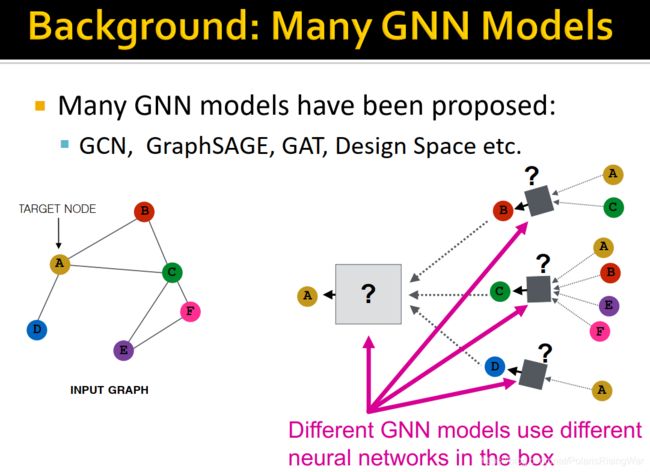
2. 本节课主要探讨，在已经提出GCN、GAT、GraphSAGE、design space等众多GNN模型的前提下，各种模型的表示能力（区分不同图结构的能力）如何？我们如何设计这样一种表示能力最强的模型？
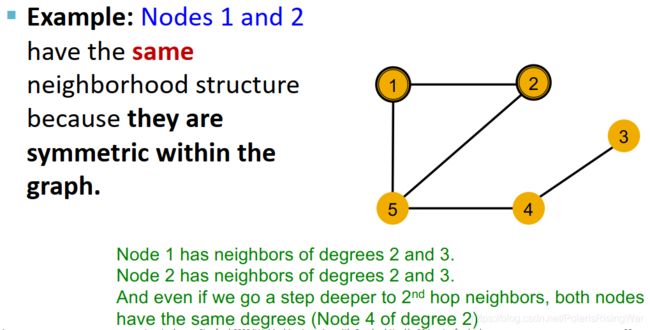
3. GNN模型实例
   1. GCN：mean-pool + Linear + ReLU non-linearity⁴
   2. GraphSAGE（以最大池化为例）：MLP + max-pool
4. 本课程中用节点颜色指代特征feature，同色即特征相同。
   如图中举例图中所有节点的特征都相同（黄色）。
   图上的信息分为结构信息和特征信息，因为特征相同，所以无法仅凭特征来区分节点了（如果特征全都不一样，只需要看特征向量就能将节点区分开了）。让所有特征相同可以更好看出GNN如何捕捉结构信息。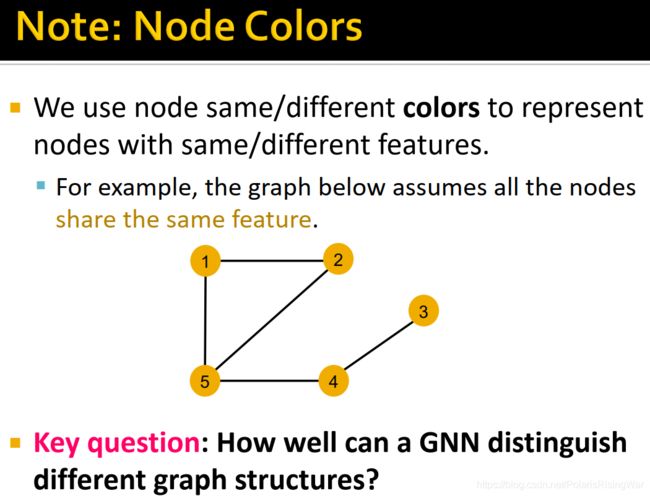
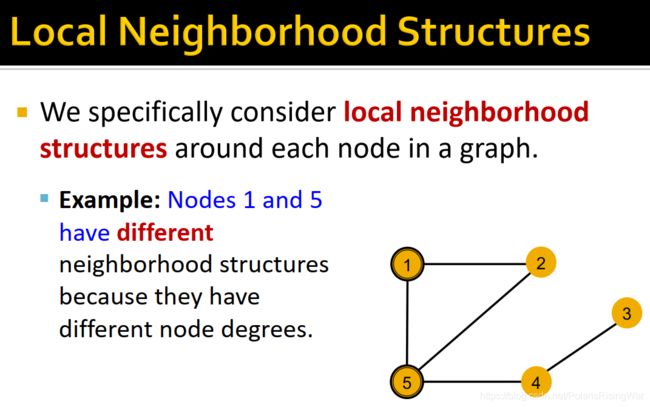
5. 局部结构信息
   我们感兴趣于量化节点的局部结构信息。
   1. 例子1：节点1和节点5，因其度数不同而具有不同的局部结构信息。
   2. 例子2：节点1和节点4，具有相同度数，但到其两跳邻居的信息上，可以区分两点：其邻居的度数不同。
   3. 例子3：节点1和节点2，具有相同的邻居结构，因为在图中是对称的。（不可区分）（无论多少跳邻居上，都具有相同的局部结构）（位置同构）
6. 我们接下来就要分析GNN节点嵌入能否区分不同节点的局部邻居结构，在什么情况下会区分失败。
   GNN通过计算图得到局部邻居结构。
7. 计算图
   1. GNN每一层聚合邻居信息（节点嵌入），即通过其邻居得到的计算图产生节点嵌入。
   2. 节点1和节点2的计算图：
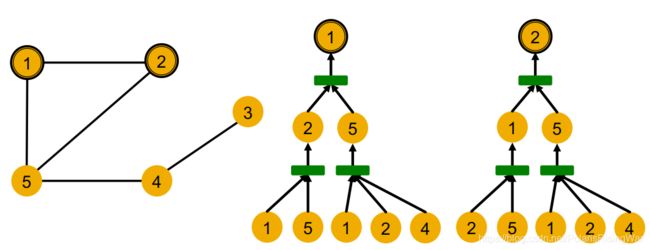
   3. 上图两个计算图本质上是一样的：GNN只能识别特征，不能识别ID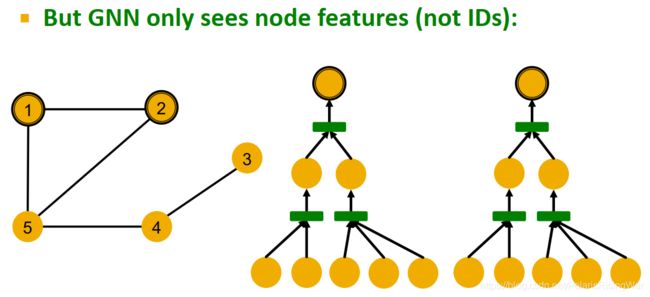因为计算图相同，这两个节点将被嵌入到同一个表示向量（即在表示域重叠，GNN无法区分这两个节点）。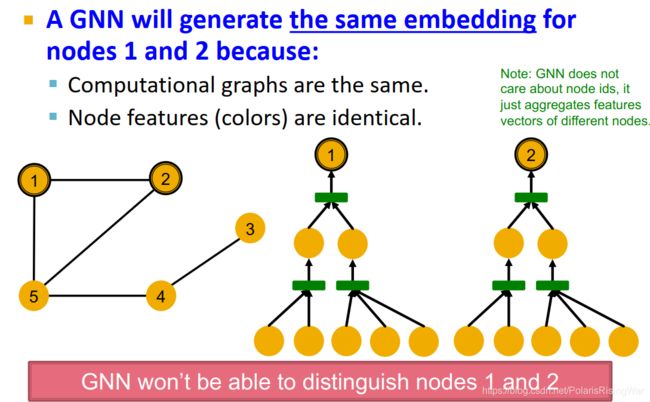
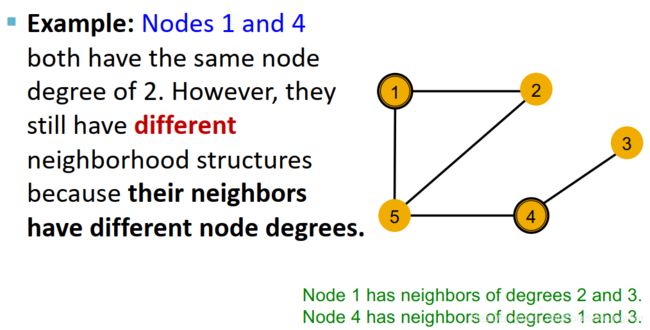
   4. 一般来说，不同的局部邻居会得到不同的计算图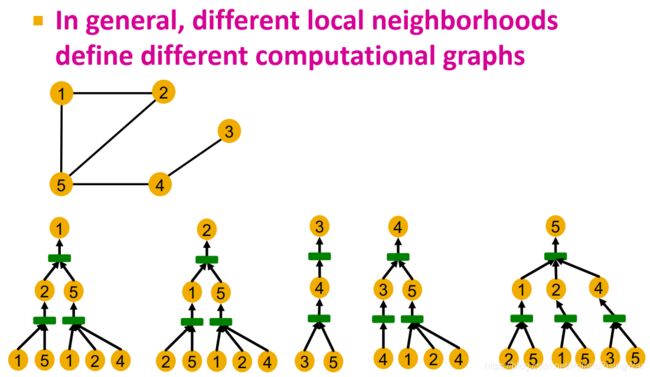：节点1和节点2由于计算图相同，所以GNN无法区分。理论上节点3、4、5由于计算图不同是可能由GNN区分开的。
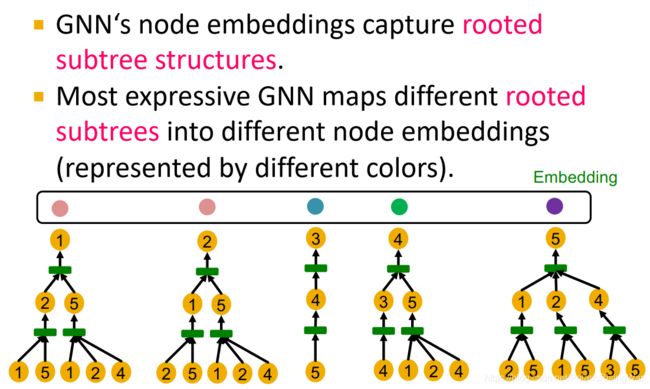
      表达能力最强的GNN能区分开任意计算图不同的节点。
   5. 计算图和对应节点的有根子树结构rooted subtree structure⁵相同，通过从根节点逐邻居展开计算图而得到。
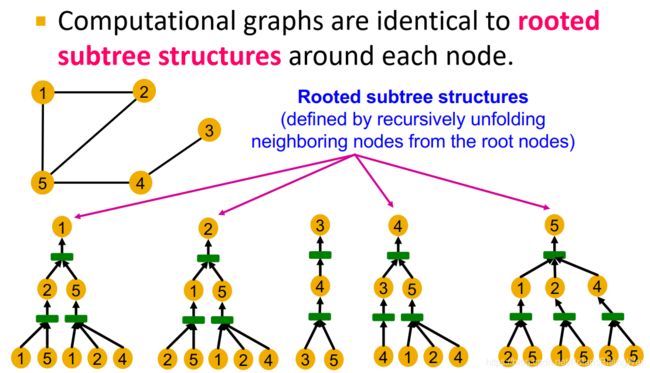
   6. GNN节点嵌入捕获这个rooted subtree structures，表示能力最强的GNN模型将不同的rooted subtree结构映射到不同的节点嵌入中（图中表示为不同颜色）：
8. 单射injective函数：将不同自变量映射为不同的因变量，这样可以完整保留输入数据中的信息
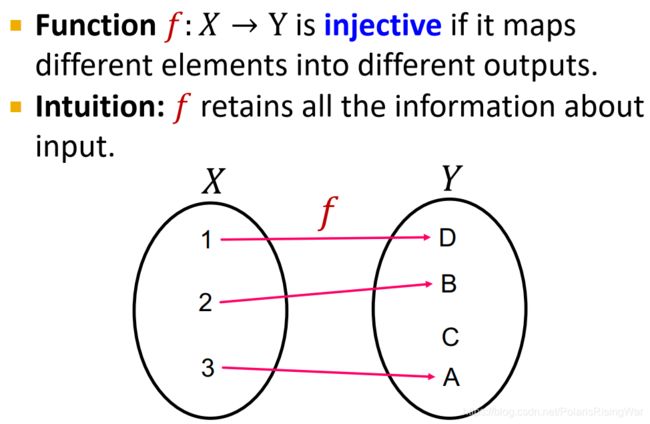
9. 表示能力最强的GNN就应该单射地映射子树到节点嵌入（即不同的子树映射为不同的嵌入）
10. 同深度的子树可以从叶节点到根节点迭代表示信息，来进行区分⁶
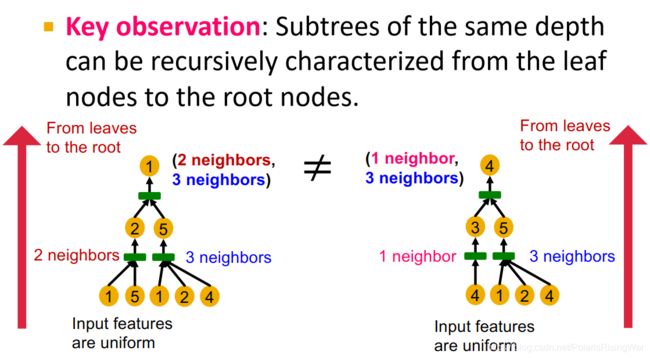
11. 如果GNN每一步聚合都可以保留全部邻居信息，那么所产生的节点嵌入就可以区分不同的有根子树，也就达成了GNN具有最强表示能力的效果。
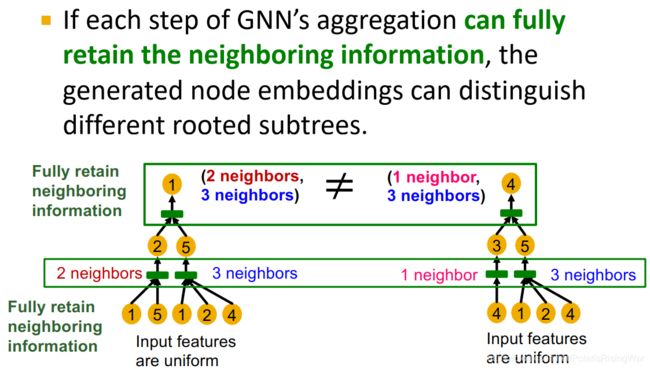
12. 所以表示能力最强的GNN就是每一步都使用单射邻居聚合函数（保留全部信息），把不同的邻居映射到不同的嵌入上。
13. 总结
    为得到节点嵌入，GNN使用计算图（以节点为根的子树），如果每层都使用单射的聚合函数，就可以达成区分不同子树的效果。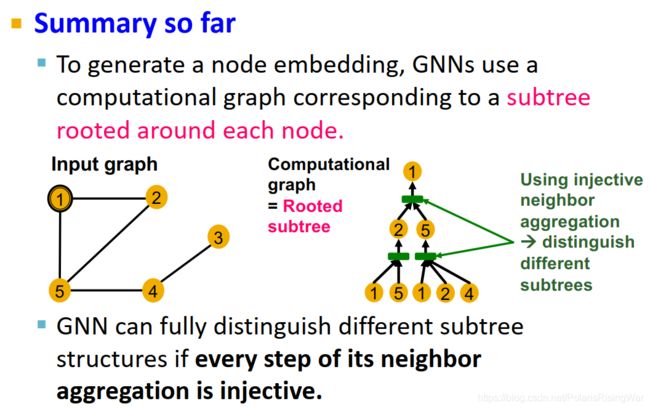

2. Designing the Most Powerful Graph Neural Network

1. GNN的表示能力取决于其应用的邻居聚合函数。聚合函数表达能力越强，GNN表达能力越强，单射聚合函数的GNN表达能力最强。
   接下来本课程将理论分析各聚合函数的表示能力。
2. 邻居聚合过程可以被抽象为multi-set（一个元素可重复的集合，在此处指节点的邻居集合，元素为节点，节点特征可重复）上的函数。如图中以圆点集合作例，点同色指特征相同：
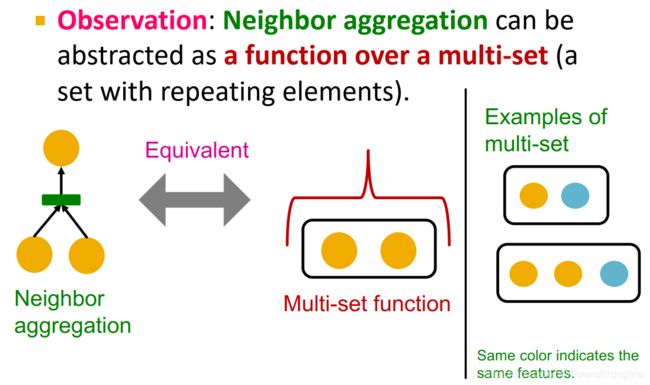
3. 接下来我们分析GCN和GraphSAGE的聚合函数
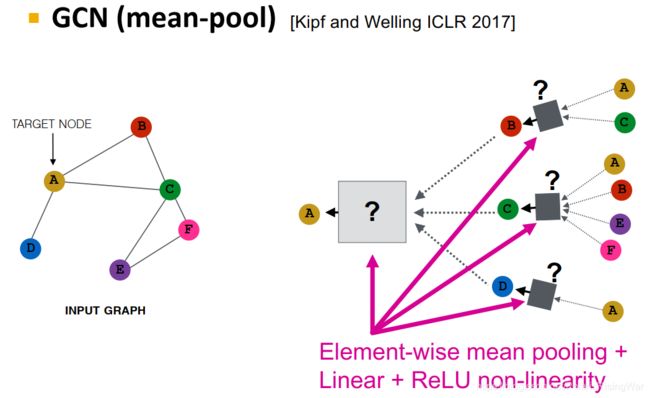
   1. GCN：mean-pool
      mean-pool + Linear + ReLU non-linearity
      根据Xu et al. ICLR 2019¹ 得到定理：GCN的聚合函数无法区分颜色占比相同的multi-set⁷。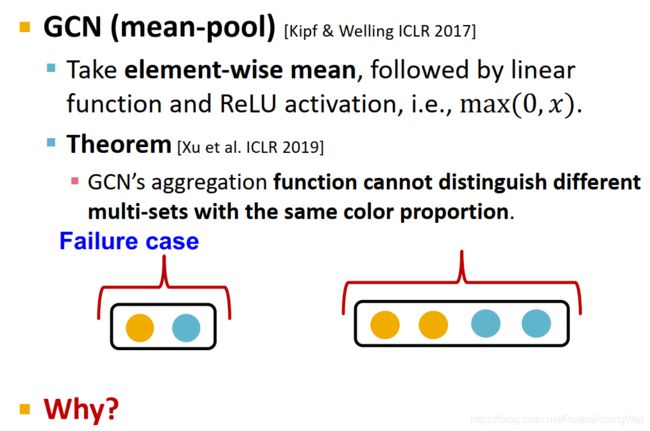
      假设不同颜色的特征是独热编码特征，如图所示黄蓝二色特征：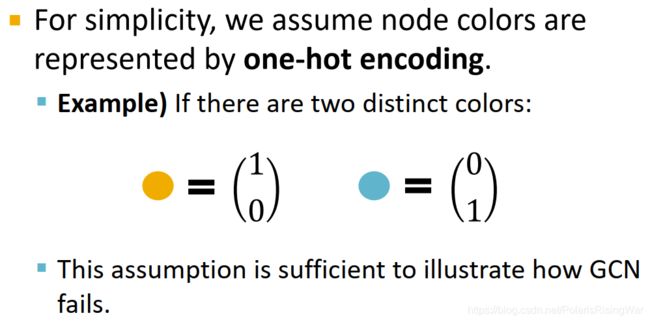
      GCN无法区分不同multi-set的一个实例：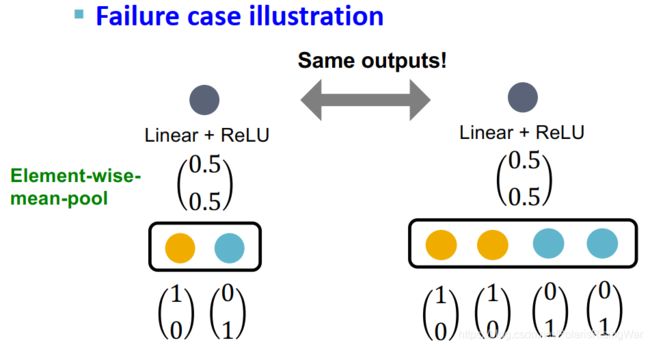
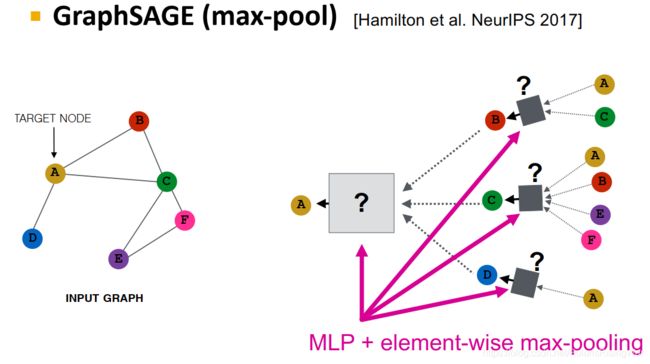
   2. GraphSAGE：max-pool
      MLP + max-pool
      根据Xu et al. ICLR 2019¹ 得到定理：GraphSAGE的聚合函数无法区分具有相同的不同颜色（即具有一样的多种颜色，或者不重复颜色组成的集合相同）⁸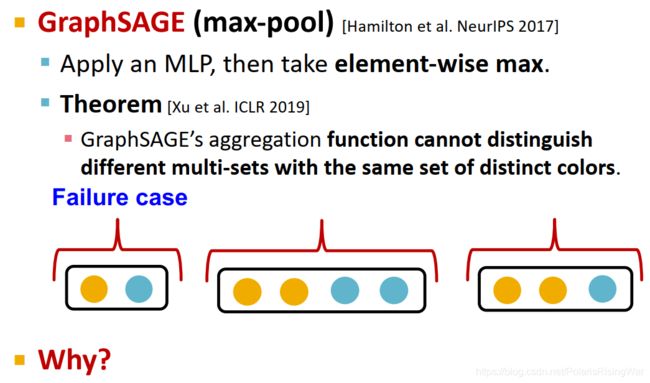
      一个失败案例：假设上一层节点嵌入经过一个单射的MLP函数形成不同的独热编码向量，经逐元素最大池化后得到相同输出：
4. 根据上文对GNN表示能力的分析，我们得出的主要结论takeaway⁹为：
   1. GNN的表示能力由其邻居聚合函数决定
   2. 邻居聚合是个multi-set上的函数，multi-set是一个元素可重复的集合
   3. GCN和GraphSAGE的聚合函数都不能区分某些基本的multi-set，因此都不单射，不够具有表达能力。
5. 我们的目标是设计信息传递框架下表示能力最强的GNN，这要求我们设计出multi-set上的单射邻居聚合函数。
   在本课程中，我们用神经网络建模单射的multi-set函数。
6. 单射的multi-set函数
   根据Xu et al. ICLR 2019¹ 得到定理：任一单射的multi-set函数都可以表示为：$\Phi \left(\sum _{x\in S}f(x)\right)$
   $\Phi$ 和 $f$ 是非线性函数
   $\sum _{x\in S}$ 在multi-set上求和
   如图所示：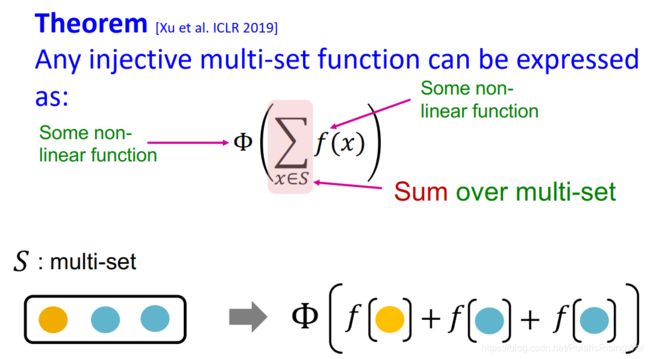
7. 一个作为证明的直觉举例¹⁰：
   $f$ 得到颜色的独热编码，对其求和就能得到输入multi-set的全部信息（每类对应向量的一个索引，每个索引的求和结果就对应该类的节点数量，就可以区分不同类任何个数的情况）
   如图所示：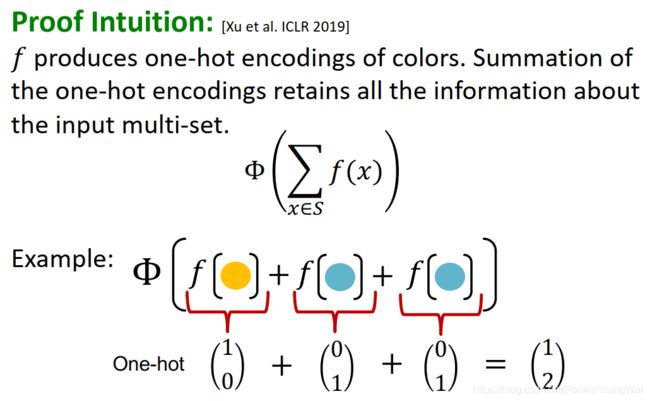
8. universal approximation theorem²
   为了建模 $\Phi \left(\sum _{x\in S}f(x)\right)$ 中的 $\Phi$ 和 $f$，我们使用MLP：因为根据 universal approximation theorem，只有一个隐藏层的MLP只要隐藏层维度够宽，并有合适的非线性函数 $\sigma (\cdot )$ （包括ReLU和sigmoid），就可以任意精度逼近任何连续函数。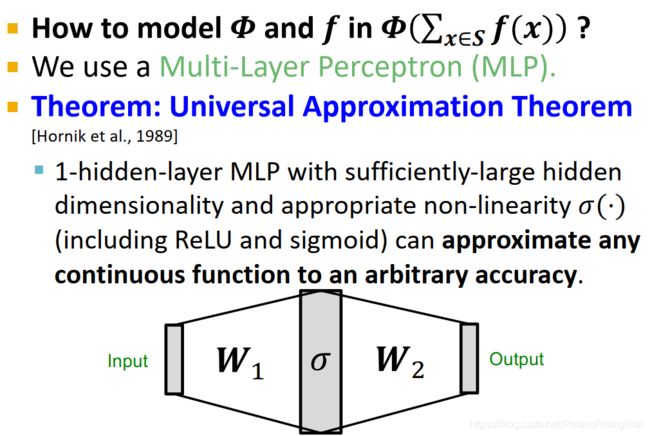
9. 应用MLP，我们可以用神经网络建模出任一单射的multiset函数，其形式即变为：${\text{MLP}}_{\Phi }\left(\sum _{x\in S}{\text{MLP}}_f(x)\right)$
   在实践中，MLP的隐藏层维度在100-500就够用了¹¹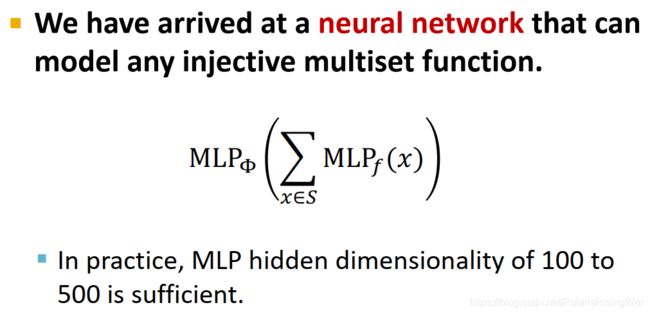
10. Graph Isomorphism Network (GIN)¹：${\text{MLP}}_{\Phi }\left(\sum _{x\in S}{\text{MLP}}_f(x)\right)$
    其聚合函数是单射的，没有区分失败的案例，是信息传递类GNN中表示能力最强的GNN
11. GIN与WL graph kernel的关系
    我们通过将GIN与WL graph kernel（获得图级别特征的传统方法）做关联，来全面了解GIN模型。
    GIN可以说是WL graph kernel的神经网络版。
12. WL graph kernel就像个硬编码的图神经网络。
    算法：color refinement
    迭代公式：$c^{(k+1)}(v)=\text{HASH}\left(c^{(k)}(v),\{c^{(k)}(u){\}}_{u\in N(v)}\right)$
    迭代至稳定¹²后，如果两个图的颜色集相同，说明它们同构。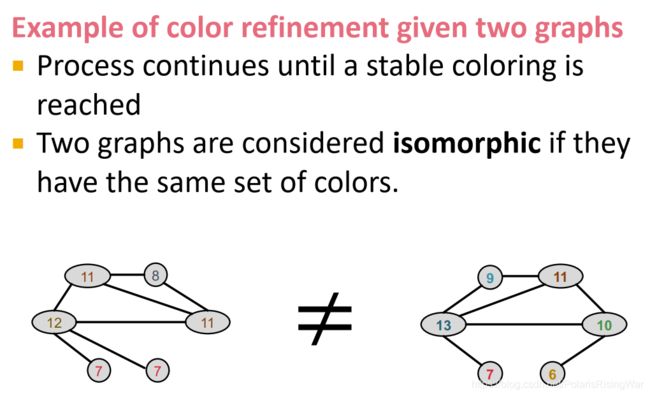
13. GIN就用一个神经网络来建模这个单射的哈希HASH函数。
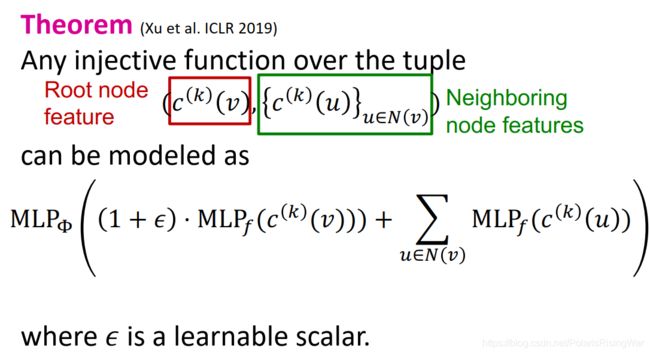
    单射函数建立在这个元组tuple上：$\left(c^{(k)}(v),\{c^{(k)}(u){\}}_{u\in N(v)}\right)$（根节点特征，邻居节点颜色）
    
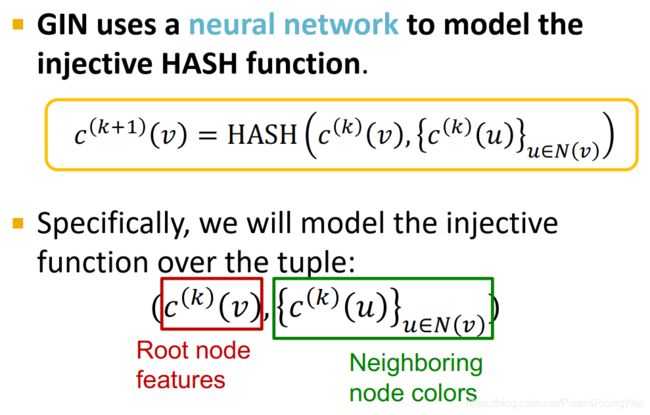
14. 根据Xu et al. ICLR 2019¹ 得到定理：这样一个元组上的单射函数可以被建模为：${\text{MLP}}_{\Phi }\left((1+ϵ)\cdot {\text{MLP}}_f(c^{(k)}(v))+\sum _{u\in N(v)}{\text{MLP}}_f(c^{(k)}(u))\right)$（$ϵ$ 是个可训练的标量）
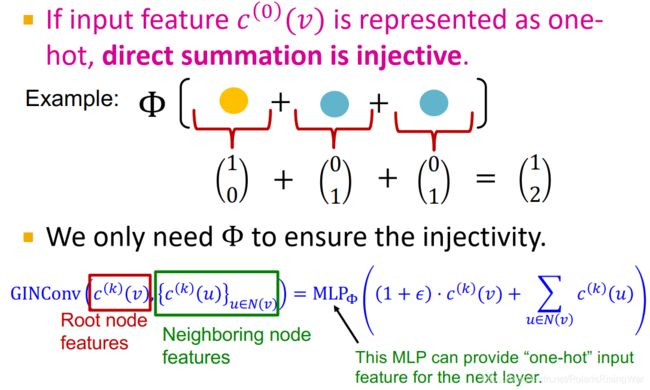
15. 如果输入特征（即初始颜色）是独热编码，那么直接加总就是单射的（跟上面的例子一样），我们就仅需 $\Phi$ 来确保函数的单射，它需要产生独热编码来作为下一层的输入特征。即：$\text{GINConv}\left(c^{(k)}(v),\{c^{(k)}(u){\}}_{u\in N(v)}\right)={\text{MLP}}_{\Phi }\left((1+ϵ)\cdot c^{(k)}(v)+\sum _{u\in N(v)}{c}^{(k)}(u)\right)$
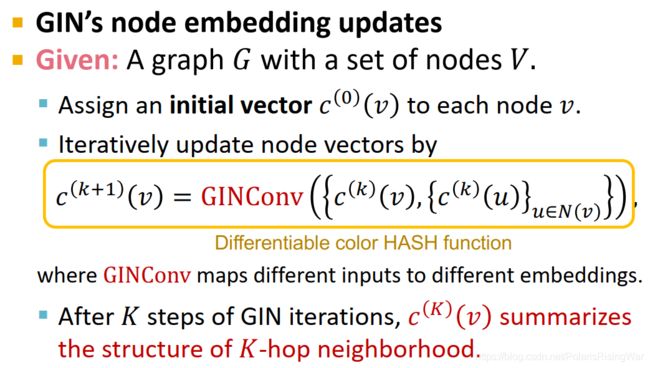
16. GIN的节点嵌入更新过程：
    1. 分配节点的初始向量 $c^{(0)}(v)$
    2. 迭代更新：$c^{(k+1)}(v)=\text{GINConv}\left(\left\{c^{(k)}(v),\{c^{(k)}(u){\}}_{u\in N(v)}\right\}\right)$
       GINConv相当于可微的color HASH函数，将不同输入映射到不同嵌入中（即单射）
    3. 经过K次迭代，$c^{(K)}(v)$ 总结得到节点 $v$ 的K跳邻居结构信息。
17. GIN和WL graph kernel
    GIN相当于可微神经网络版的WL graph kernel

	更新目标	更新函数
WL graph kernel	节点颜色（独热编码13）	HASH
GIN	节点嵌入（低维向量）	GINConv

GIN相较于WL graph kernel的优点在于：

• 节点嵌入是低维的，因此可以捕获到细粒度的节点相似性¹⁴
• GINConv的参数可被学习得到并应用于下流任务¹⁵

18. GIN的表示能力
    由于GIN与WL graph kernel之间的关系，二者的表示能力是相同的，也就是对于一样的图，要么二者都能区分，要么都不能区分。
    在理论上和实践上，WL graph kernel都能区分现实世界的大部分图¹⁶，因此GIN也能区分现实世界的大部分图。
19. 本节课总结
    1. 我们设计了一个可以建模单射的multi-set函数的神经网络
    2. 我们用这个神经网络来聚合邻居信息，得到GIN：表示能力最强的GNN模型
    3. 关键在于用element-wise sum pooling代替mean-/max-pooling
    4. GIN与WL graph kernel有关
    5. GIN和WL graph kernel都能区分现实世界的大部分图
20. 各种池化方法的能力：
    sum能区分整个multiset，mean只能区分不同的分布，max只能区分元素类型集合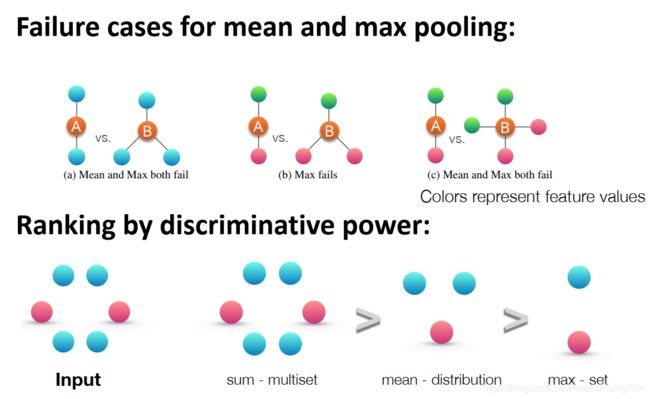
21. 增加GNN的表示能力
    对于类似“节点处于不同环中”这种问题，GNN仍然无法区分（因为计算图相同）。解决方法可以是添加可区分节点的feature¹⁷，也可以使用reference node来区分相同计算图等。后续课程将会讲述具体做法。
    参考论文：^{18 19}

---

1. Xu, Bingbing & Shen, Huawei & Cao, Qi & Qiu, Yunqi & Cheng, Xueqi. (2019). Graph Wavelet Neural Network. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

2. Kurt Hornik, Maxwell Stinchcombe, and Halbert White. Multilayer feedforward networks are universal approximators. Neural networks, 2(5):359–366, 1989.
   一个对该论文进行简单解读的博文：Multilayer Feedforward Networks are Universal Approximators_hn18000的专栏-CSDN博客
   我从这个网址下载了论文，去掉水印页，上传到GitHub，可供下载。 ↩︎ ↩︎

3. 可参考我之前撰写的笔记：cs224w（图机器学习）2021冬季课程学习笔记2: Traditional Methods for ML on Graphs ↩︎ ↩︎

4. 可参考我之前撰写的笔记：cs224w（图机器学习）2021冬季课程学习笔记9 Graph Neural Networks 2: Design Space ↩︎

5. 我没看懂这部分什么意思……计算图和每个节点的rooted subtree结构一样是什么意思？
   我查了一下，subtree是树中也是树的子图（Definition:Subtree (Graph Theory)），rooted subtree是以原根节点为根节点的subtree（Definition:Rooted Subtree），所以我能理解计算图的有根子树互相之间是一样的（就是，迭代嘛，1的计算图里面有2和5的计算图的有根子树……这种感觉。我是这样理解的）。
   还是说这个子树指的是原图中以逐层邻居形成的子树（也就是计算图）？
   但是这部分具体在说什么我没搞懂。我感觉不影响我对全课纲要的理解，以后再研究这是啥意思吧。 ↩︎

6. 我没看懂这张PPT是啥意思。大概意思是GNN每一步都聚集、存储来自孩子节点的信息，然后将其传播到父节点上，如此逐层传递的意思？ ↩︎

7. 就我感觉这个定理就挺直觉的……但是要证明也不会证明。 ↩︎

8. 就这个定理更直觉了嘛，一种颜色所代表的最大值就唯一了，只要有这种颜色在就只能得到一种结果，那不管这种颜色有多少个都不影响结果。
   也就是说，只要保证每个multi-set里面都有所有的颜色种类就行，具体每个颜色多少个点无所谓。 ↩︎

9. takeaway: a conclusion to be made based on presented facts or information
   来源：Takeaway | Definition of Takeaway by Merriam-Webster ↩︎

10. 用这个例子作为证明应该是合理的，毕竟这个定理是“可以这样表示”，而例子就是证明这一点。 ↩︎

11. 我看懂了MLP可以用来拟合出这样一个单射的函数，但是我怎么确定这样形成的函数是单射的？就是，我的目标函数要如何定义，才能训练出单射的效果？
    这部分我没搞懂。 ↩︎

12. 这玩意真的能稳定吗我就没搞懂，我本来就没太搞懂这个算法……以后再看吧 ↩︎

13. 关于节点颜色是什么表现形式其实我没搞懂，既然它说是独热的那就独热吧 ↩︎

14. 关于为什么说低维向量的节点嵌入能够捕获节点相似性，我认为是因为节点嵌入就是一个向量嘛，可以根据向量之间的运算来得到节点相似性。就独热编码的话全部正交，肯定没有相似性可言了。
    但是为啥是细粒度的我没搞懂。 ↩︎

15. 更新目标是节点嵌入，可应用于下流任务我懂，这个参数指的是那个$ϵ$？这玩意怎么应用于下游任务？ ↩︎

16. Jin-Yi Cai, Martin Fürer, and Neil Immerman. An optimal lower bound on the number of variables for graph identification. Combinatorica, 12(4):389–410, 1992 ↩︎

17. 可参考我之前撰写的笔记：cs224w（图机器学习）2021冬季课程学习笔记10 Applications of Graph Neural Networks ↩︎

18. Identity-aware Graph Neural Networks
    Jiaxuan You, Jonathan Gomes-Selman, Rex Ying, Jure Leskovec
    35th AAAI Conference on Artificial Intelligence (AAAI 2021)
    PDF
    Code
    Webpage ↩︎

19. Distance Encoding: Design Provably More Powerful Neural Networks for Graph Representation Learning ↩︎