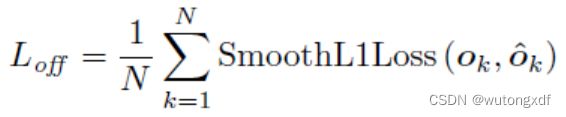目标检测论文阶段性总结——Anchor-Free Detectors

目录

背景（针对 anchor-based model）

CornerNet

1. 主干网络——Hourglass Network

2. Detecting Corner-Pairs

1) Heatmaps

2）Offests 

3) Embedding vectors

 3. Corner Pooling

缺点

FCOS

1. 主要框架

2. FPN 结构

3. Center-ness

4. Center Sampling 

---

背景（针对 anchor-based model）

此前先进的目标检测模型几乎都使用了 anchor box，存在以下问题：

1. Anchor box 的设置往往非常密集，但真正与 ground truth产生重合的很少，造成了正负样本之间极大的不平衡；

2. 使用 anchor box 会产生大量需要人工选择的超参数，如 box 的数量、尺寸、长宽比等；

3. Anchor box 的尺寸、长宽比的设计是固定的，难以覆盖所有形状的目标，泛化能力差；

4. Anchor box 产生了一些复杂的计算，如计算 IoU 等。

CornerNet

1. 主干网络——Hourglass Network

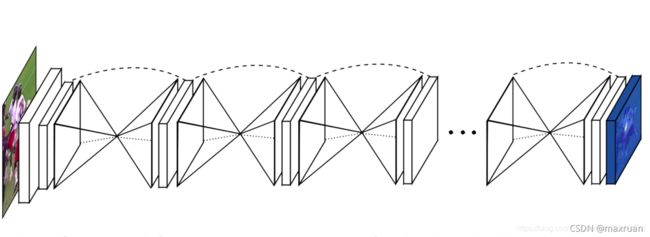
沙漏（Hourglass） 网络是全卷积网络，包含一个或者多个 Hourglass 模块。

沙漏网络先由卷积和池化将特征图下采样到一个很小的尺度，之后再用nearest neighbor upsampling 的方法进行上采样，将特征图还原到最开始的尺度。不难看出，下采样和上采样是对称的，并且在每个 上采样层都使用残差模（residual modules）块进行跳连（skip connection）。

使用这种沙漏结构的目的是为了反复获取不同尺度下图片所包含的信息，沙漏结构可以获取局部信息和全局信息。

沙漏网络图片和讲解来源：CornerNet详解_maxruan的博客-CSDN博客_cornernet

CornerNet 使用的沙漏网络使用了两个 hourglasses。

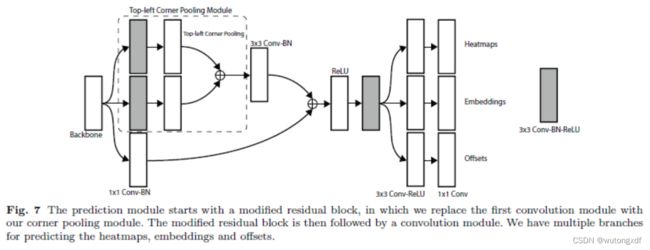
2. Detecting Corner-Pairs

将对一个目标的检测看成一对关键点（左上和右下）的检测。

具体来说，网络分别输出代表不同种类目标位置的左上角热力图、右下角热力图；检测到的每个角点的嵌入向量，用于对属于同一目标的一对角点进行分组；以及offsets，用于对corner的位置进行修正。

1) Heatmaps

含有 C 个通道的二元掩码，大小为H×W，C为类别数量（不含背景），预测哪些位置最可能是角点。

对于每个角点来说，只有一个 ground truth 是正样本，其余都是负样本，但对于那些位于 GT 某半径范围内的负样本会减轻惩罚，如下图：

惩罚量由一个非标准的二维高斯函数计算得到，该函数以正位置（GT）为中心，σ 为半径的1/3。

Heatmap（detection）采用改良版的 focal loss 计算损失，损失函数如下：

其中， 为热力图上（i,j）位置属于 c 类别的置信度分值， 是经过高斯函数加强后的 GT 热力图。若刚好落在 GT 位置，则  ；若落在 GT 某半径内，则  按照高斯分布逐渐向外递减。 计算后越接近于1，则受到的惩罚越小。

2）Offests 

所有类别的左上角共享一组预测出的偏移，右下角同理。

其中  表示偏移量， 和  是角点 k 的x、y坐标。作者在 GT 角点位置使用 Smooth L1 Loss：

3) Embedding vectors

作者采用的嵌入向量（embedding vector ）是一维的，embedding 实际的值并不重要，作者的目的在于：基于不同角点的嵌入向量之间的距离找到每个目标对应的一对角点，如果一个左上角角点和一个右下角角点属于同一个目标，那么二者嵌入向量之间的距离应该很小。

作者用 “pull” 损失来训练网络聚合同组角点，用 "push" 损失来分离不同组的角点。

其中， ， 分别表示第 k 个目标的左上、右下角点的 embeddings， 表示两者的均值。对于同组的角点，作者希望它们尽量接近均值（如果只是让embedding接近，那么在反向传播的过程中可能会overshoot）；对于不同组的角点，作者希望它们不要靠的过近。

总体损失函数为几类损失的加权和：

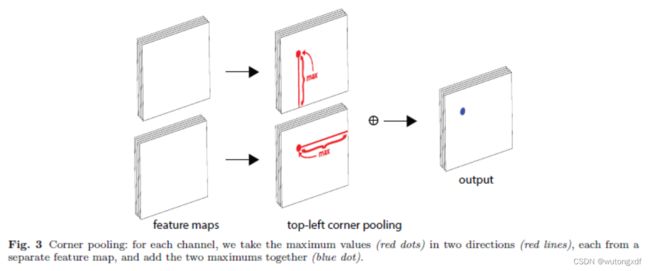
 3. Corner Pooling

如上图所示，角点位置本身往往并不存在视觉证据。即在目标检测的任务中，目标的角点往往在目标之外，所以针对角点的检测不能依赖局部特征，而应对该点所在行、列的所有特征进行扫描。

作者基于这种观察提出了 Corner Pooling 的方法。

 

 

 作者自右向左、自下而上，逐元素进行最大池化操作。

缺点

需要比较复杂的后处理，如将属于同一目标的两个角点归为一组，引入了额外的距离衡量指标。

FCOS

作者借鉴了FCN的思想，对每个点直接进行预测，输出当前位置距离 bounding box上、下、左、右边四个边缘的距离（t,b,l,r）。

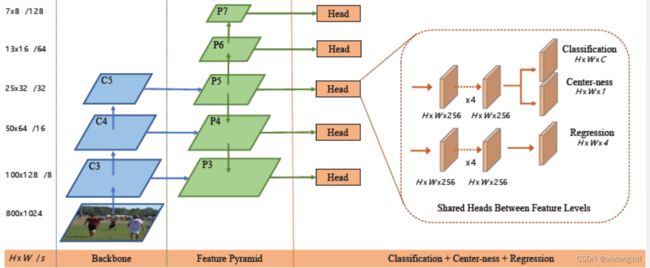
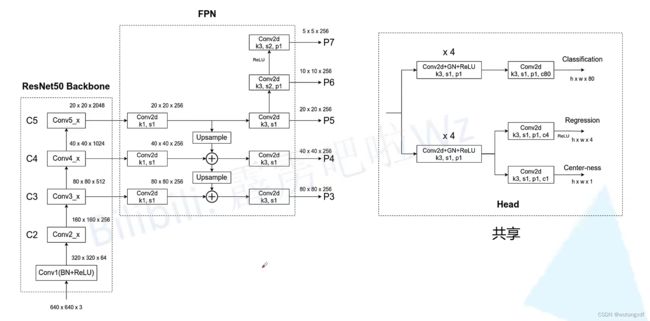
1. 主要框架

图片来源：FCOS网络讲解_哔哩哔哩_bilibili 

FCOS 的 backbone 使用 RetinaNet，共有5个预测特征层，对应的5个 head 共享参数（五个预测特征层共享同一个head）。

每个head 有3个预测分支：

1) classification branch：在预测特征图的每个位置上预测 C 个类别概率（C个二分类器）；

2) regression branch：在预测特征图的每个位置上预测4个距离参数 (l,t,r,b)，预测的尺度是相对于特征图尺度而言的；

左上角：     

右下角：    

其中， 为当前点映射回原图的坐标，s 为特征图到原图的步距。

3) center-ness branch：反映该位置（特征图赏某点）距离目标中心点的远近程度，值域∈ [0,1]。

总体损失函数为：

2. FPN 结构

为了解决同一个点落入多个 ground truth box 相交区域的 “intractable ambiguity” 的问题，作者引入了 FPN 结构。

为了达到与anchor-based方法相似的“不同层级对应不同大小锚框”的效果，FCOS直接在不同特征图基础上限制bbox的回归范围，与不同特征图的步长相对应，具体如下：

【注】由于 FCOS 的各个预测特征层共享 head，但是不用layer的回归尺度也不同，所以这里作者增加了一个可训练的比例调节因子  ，使用对边界框的回归进行处理，调节各层的回归尺度。

3. Center-ness

作者引入了一个与 classification branch 平行的 center-ness branch（第二版改为与regression branch 平行），用以改善很多低质量的预测框距离目标中心较远的情况。

 为真实标签值， 为当前点距离 GT bounding box 边缘的距离。当前点接近 GT box 边界处时，；恰好落在 GT box 中心时，。

在inference阶段，将该center-ness的值与classification branch 输出的置信度值相乘，可以有效过滤一批误检框，提高识别准确度。

4. Center Sampling 

第一版中，只要当前预测点落入 GT box 所包含的范围内，即为正样本；

在第二版中，作者对于正样本的选择也作出了改变，只有落入 sub-box 中的预测点，才为正样本。

图片来源：FCOS网络讲解_哔哩哔哩_bilibili

上图中， 分别对应 sub-box 左上和右下角的坐标，s 为预测特征图相对于原图的步距，r 为一个超参数。