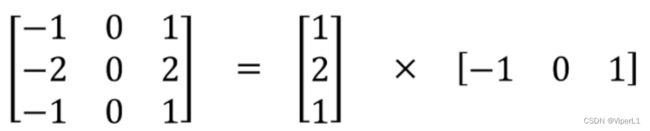卷积运算与卷积核DLC
一、卷积运算
在数学上，卷积的定义是：两个函数在反转和位移后的乘积的积分，其公式表现为：
其中称g为过滤器，f为信号。
但是在深度学习中，卷积并不进行反转，而是直接进行逐元素的乘法和加法（称互相关：一般通过窗口的滑动实现）
二、图像处理中的卷积核
卷积核在图像处理中实际上等于像素的9合1（由于扫描方式不一定准确），形式如下图
卷积核在图像处理中一般有以下作用：保持、边缘检测、锐化、滤波
卷积核通过调整像素之间的权重关系来实现对图片的修改，大致可以分为强化权重比(边缘检测&锐化)和削弱权重比两种。
且权重之和大于1时，会提高图片的亮度；权重之和小于1时，会降低图像亮度；权重之和等于1时，则保持亮度不变。
例如边缘检测的卷积核可以放大某个方向上的像素点骤变。
上面两个卷积核分别可以检测对角方向、水平&垂直方向的边缘
又如模糊可以通过降低图像各像素之间的权重比来压制突出的特征。
上面的卷积核会使像素点的权重降低为原来的1/9，从而改变权重比重
三、不同尺寸卷积核的作用
1x1卷积核
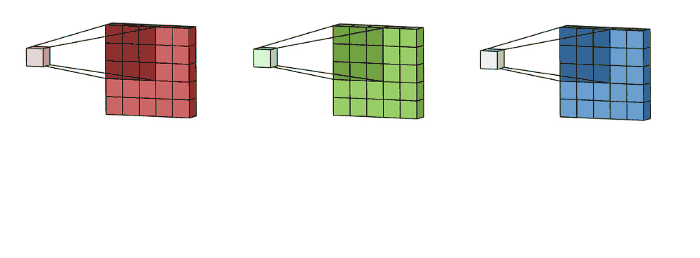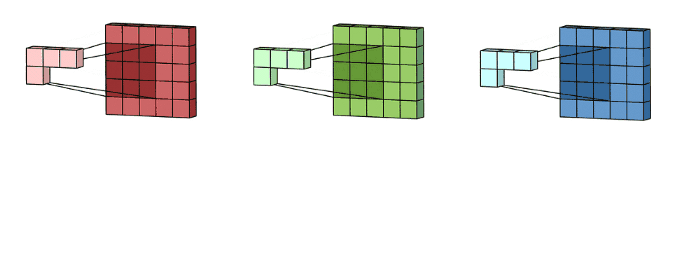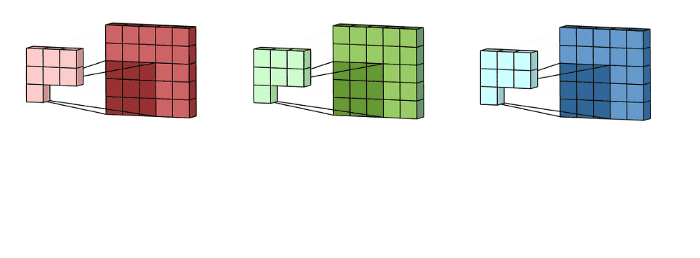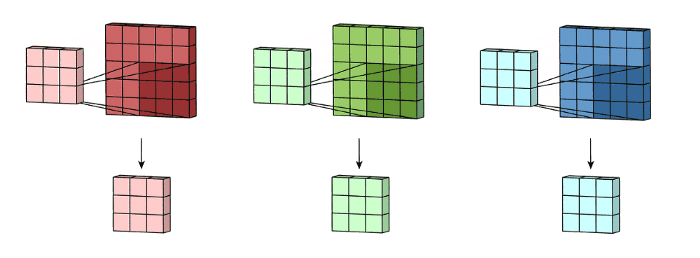
降维/升维：通过1x1卷积核的图像在平面上(width和height)并不会有任何改变，但是其通道(channel)数会增加/减少。
同时，应为卷积运算和全连接运算形式上的一致，1x1卷积核可以等价为一个全连接。也是卷积层可以代替全连接层将NN变为CNN的原理。
如一个6x6x32的图像经过1x1x2的卷积核后会得到6x6x2的输出，其channel降低了
又如6x6x32的图像经过1x1x128的卷积核后得到6x6x128，其channel便上升了
其在网络中通过升降维可以实现：
增加非线性：在保持feature map尺寸不变的前提下增加其非线性特性，从而加深网络层数。
跨通道信息交互：将不同卷积核处理过的特征图统一channel，以便后续运算。
nxn卷积核
包括常用的3x3，5x5以及更大尺寸的卷积核。一般作为滤波器(filter)来抓取图像特征。
卷积核尺寸越大，感受野越大，一次获取的特征便越多；但是精确度会下降。同时也会带来更大的计算压力（）。
如3x3卷积核的感受野为9，而5x5卷积核的感受野为25，基本可以理解为一个5x5卷积核近似于两个3x3卷积核（3x3=9*2=18<5x5=25）。
一般来说超过9x9的kernel会被视为大kernel
四、卷积核的性质
卷积核的主要超参数有：卷积核个数k个，尺寸w*h，步长s，填充p
参数量为
//(长*宽*高+1)*个数<没有高用输入深度代替>
输入图像
经过卷积核处理后的输出为：
2D卷积：
//一般卷积核为nxn的矩阵，故可以归纳为：
//
//卷积核个数
输入层：
卷积核尺寸：
参数量：
3D卷积：三个维度尺寸W*H*D同二维卷积：
//卷积核个数
特殊的卷积：空洞卷积、可分离卷积、转置卷积
转置卷积：又称反卷积，上采样，与一般卷积互为逆操作，可用来恢复原来的尺寸。
卷积核与一般卷积并无区别。步长为原来步长的倒数，即
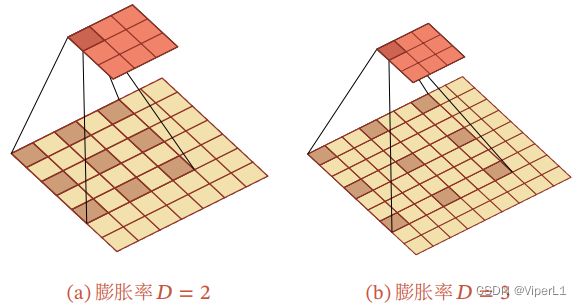
空洞卷积：又称下采样。主要作用是在不增加参数数量(增加卷积核大小/增加层数)和不丢失信息(卷积前进行汇聚)的前提下增大卷积核的感受野。具体操作为：在卷积核的每个元素之间插入D-1个空洞，使得卷积核的有效大小变为：
,D被称为膨胀率。
可分离卷积：分为空间可分离卷积和深度可分离卷积。
空间可分离卷积有个条件，即卷积核可以拆分为向量的积。
空间可分离卷积可以减少参数的个数，节约成本，但一般不用于训练。
深度可分离卷积：将卷积核拆分为三个向量的积，目前没有用过，以后用到再回来学习。