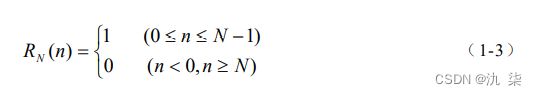数字信号处理一:离散时间信号的表示及运算
离散时间信号是指在离散时刻才有定义的信号,简称离散信号,或者序列。离散序列通常用 x(n) 来表示,自变量必须是整数。
离散时间信号的波形绘制用 matplotlib.pyplot 中的 stem 函数。由于矩阵元素的个数有限,所以只能表示一定时间范围内有限长度的序列;而对于无限长的序列,也只能在一定时间范围内表示出来。
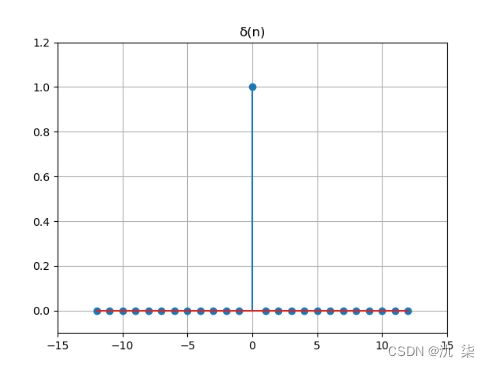
1. 单位脉冲序列
要注意,单位脉冲序列不是单位冲激函数的简单离散抽样,它在 n=0 处是取确定的值 1。
程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-12
n2=12
L=n2-n1+1
n=np.linspace(n1,n2,L)
a1 = np.zeros(L)#只有n=0时, a1=1;当n≠0时,a1=0
a1[n0-n1] = 1
plt.ylim(-0.1,1.2)
plt.xlim(-15,15)
plt.stem(n,a1)# 画棉棒
plt.title('δ(n)')
plt.grid('on')# 显示网格线
plt.show()
np.linspace(start, stop, num, endpoint, retstep, dtype)
star和stop为起始和终止位置,均为标量
num为包括start和stop的间隔点总数,默认为50
endpoint为bool值,为False时将会去掉最后一个点计算间隔
restep为bool值,为True时会同时返回数据列表和间隔值
dtype默认为输入变量的类型,给定类型后将会把生成的数组类型转为目标类型
2. 单位阶跃序列 u(n)
程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-10
n2=15
L=n2-n1+1
n=np.linspace(n1,n2,L)
a2 = np.zeros(n2-n1+1)
a2[(n0-n1):] = 1# 只有n>=0时, x=1;当n<0时,x=0
plt.ylim(-0.1,1.2)
plt.xlim(-12,18)
plt.stem(n,a2)
plt.title('u(n)')
plt.grid('on')
plt.show()
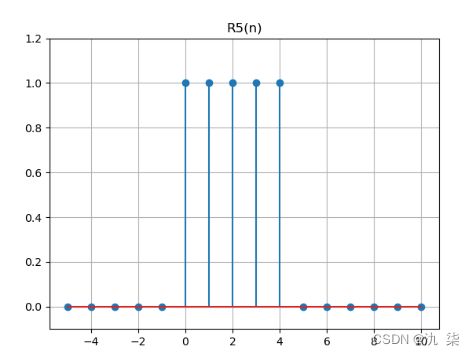
3. 矩形序列 R N(n)
矩形序列有一个重要的参数,就是序列宽度 N。 R (n) N 与 u(n) 之间的关系为:
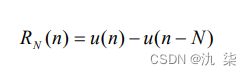
程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-5
n2=10
N=5
L=n2-n1+1
n=np.linspace(n1,n2,L)
a3 = np.zeros(L)
a3[(n0-n1):(n0-n1+N)] = 1
plt.ylim(-0.1,1.2)
plt.stem(n,a3)
plt.title('R5(n)')
plt.grid('on')
plt.show()
4. 单边指数序列
单边指数序列 n 的取值范围为 n 0 。
【 实 例 1-4 】 分 别 绘 制 单 边 指 数 序 列![]()
![]()
的波形图。
程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-5
n2=20
L=n2-n1+1
n=np.linspace(n1,n2,L)
un = np.zeros(n2-n1+1)
un[(n0-n1):] = 1
a1=1.2
a2=-1.2
a3=0.8
a4=-0.8
x1=(a1**n)*un
x2=(a2**n)*un
x3=(a3**n)*un
x4=(a4**n)*un
plt.figure('signal',figsize=(16,12))
plt.subplot(221)
plt.stem(n,x1)
plt.xlabel('n')
plt.ylabel('x(n)')
plt.title('(1.2)^n')
plt.grid('on')
plt.subplot(222)
plt.stem(n,x2)
plt.xlabel('n')
plt.ylabel('x(n)')
plt.title('(-1.2)^n')
plt.grid('on')
plt.subplot(223)
plt.stem(n,x3)
plt.xlabel('n')
plt.ylabel('x(n)')
plt.title('(0.8)^n')
plt.grid('on')
plt.subplot(224)
plt.stem(n,x4)
plt.xlabel('n')
plt.ylabel('x(n)')
plt.title('(-0.8)^n')
plt.grid('on')
plt.show()
从图可知,当 | a |> 1时,单边指数序列发散;当 | a |< 1时,该序列收敛。当 a > 0 时,该序列均取正值;当 a < 0时,序列值正负摆动。
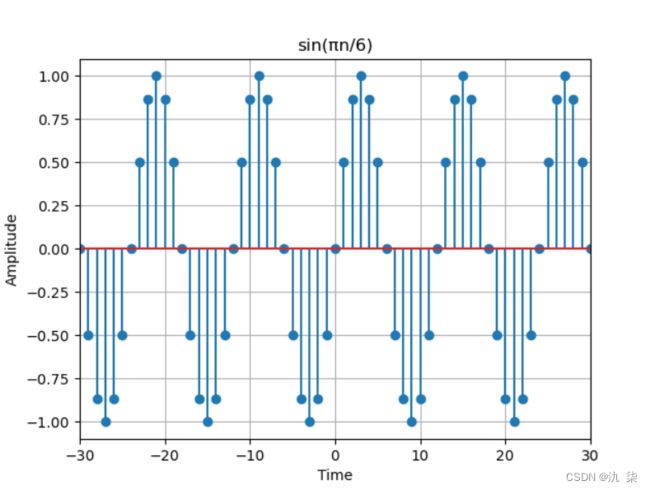
5. 正弦序列
程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-30
n2=30
L=n2-n1+1
PI=np.pi
w=1/6
n=np.linspace(n1,n2,L)
x=np.sin(w*PI*n)
plt.stem(n,x)
plt.ylim(-1.1,1.1)
plt.xlim(-30,30)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('sin(πn/6)')
plt.grid('on')
plt.show()
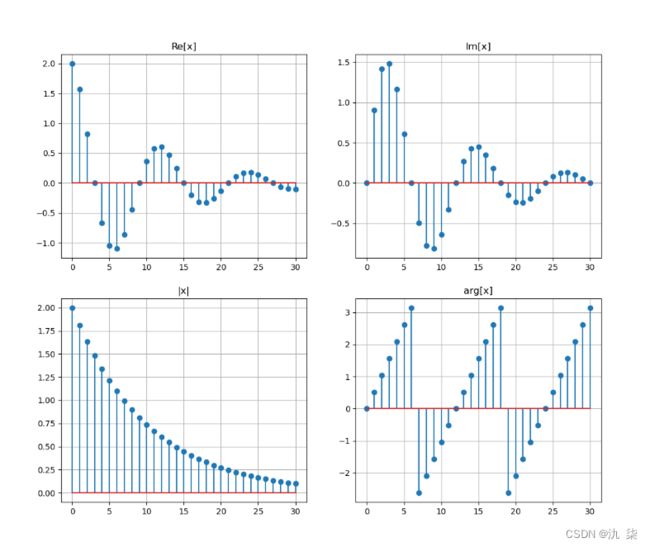
6. 复指数序列
画出复指数序列 的实部、虚部、模及相角随时间变化的曲线,并观察其时域特性。程序代码示例如下:
的实部、虚部、模及相角随时间变化的曲线,并观察其时域特性。程序代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
n1=0
n2=30
L=n2-n1+1
n=np.linspace(n1,n2,L)
A=2
a=-1/10
PI=np.pi
b=PI*1/6
c=complex(a,b)
x=A*np.exp(c*n)
plt.figure('signal',figsize=(12,10))
plt.subplot(2,2,1)
plt.stem(n,x.real)
plt.title('Re[x]')
plt.grid('on')
plt.subplot(2,2,2)
plt.stem(n,x.imag)
plt.title('Im[x]')
plt.grid('on')
plt.subplot(2,2,3)
plt.stem(n,np.abs(x))
plt.title('|x|')
plt.grid('on')
plt.subplot(2,2,4)
plt.stem(n,np.angle(x))
plt.title('arg[x]')
plt.grid('on')
plt.show()
每日“大饼”:
每一次跌倒都是为了华丽的站起来