NNDL 实验五 前馈神经网络(1)二分类任务
目录
4.1 神经元
4.1.1 净活性值
4.1.2 激活函数
4.1.2.1 Sigmoid 型函数
4.1.2.2 ReLU型函数
4.2 基于前馈神经网络的二分类任务
4.2.1 数据集构建
4.2.2 模型构建
4.2.2.1 线性层算子
4.2.2.2 Logistic算子(激活函数)
4.2.2.3 层的串行组合
4.2.3 损失函数
4.2.4 模型优化
4.2.4.1 反向传播算法
4.2.4.2 损失函数
4.2.4.3 Logistic算子
4.2.4.4 线性层
4.2.4.5 整个网络
4.2.4.6 优化器
4.2.5 完善Runner类:RunnerV2_1
4.2.6 模型训练
4.2.7 性能评价
总结
4.1 神经元
4.1.1 净活性值
净活性值z经过一个非线性函数f(·)后,得到神经元的活性值a
使用pytorch计算一组输入的净活性值,代码参考paddle例题:
import torch
# 2个特征数为5的样本
X = torch.rand(size=[2, 5])
# 含有5个参数的权重向量
w = torch.rand(size=[5, 1])
# 偏置项
b = torch.rand(size=[1, 1])
# 使用'torch.matmul'实现矩阵相乘
z = torch.matmul(X, w) + b
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)输出
在飞桨中,可以使用nn.Linear完成输入张量的上述变换。
在pytorch中学习相应函数torch.nn.Linear(features_in, features_out, bias=False)。
实现上面的例子,完成代码,进一步深入研究torch.nn.Linear()的使用。
import torch
import torch.nn as nn
from torch.autograd import Variable
m = nn.Linear(5, 1)
input = Variable(torch.rand(2, 5)) #包装Tensor使得支持自动微分
output = m(input)
print(output)
输出
torch.nn.Linear()的使用:
class torch.nn.Linear(in_features,out_features,bias = True )
【思考题】加权相加与仿射变换之间有什么区别和联系?
常数加权相加表示两个操作数均是常数(可是整数、浮点数等实数),同时还输入一个权重系数,而仿射变换主要包括平移变换、旋转变换、尺度变换、倾斜变换(也叫错切变换、剪切变换、偏移变换)、翻转变换,一共有六个自由度(平移包括x方向平移和y方向平移,算两个自由度)。
特点:
仿射变换保持二维图形的平直性和平行性,但是角度会改变
1> 平直性:变换后直线还是直线、圆弧依旧是圆弧;
2> 平行性:平行线依旧平行,直线上点的位置顺序不变。
仿射变换的6个自由度中旋转占4个,另外两个是平移。它能保持平行性,但是不能保持垂直性(因为存在倾斜变换)。
4.1.2 激活函数
激活函数通常为非线性函数,可以增强神经网络的表示能力和学习能力。
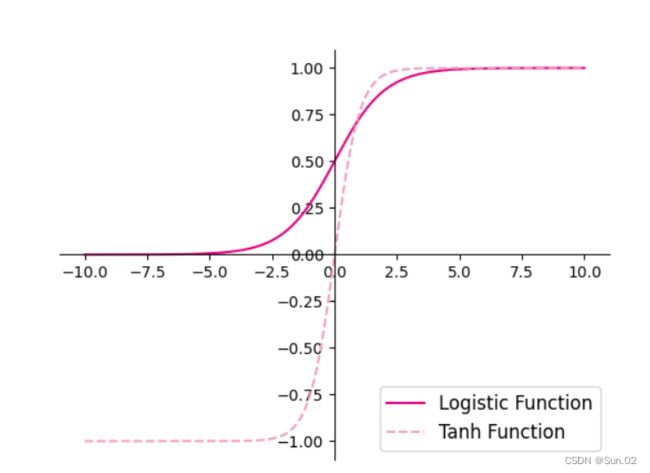
常用的激活函数有S型函数和ReLU函数。
Logistic函数:
![]()
Tanh函数:
4.1.2.1 Sigmoid 型函数
常用的 Sigmoid 型函数有 Logistic 函数和 Tanh 函数。
1.使用python实现并可视化“Logistic函数、Tanh函数”
import torch
import matplotlib.pyplot as plt
# Logistic函数
def logistic(z):
return 1.0 / (1.0 + torch.exp(-z))
# Tanh函数
def tanh(z):
return (torch.exp(z) - torch.exp(-z)) / (torch.exp(z) + torch.exp(-z))
# 在[-10,10]的范围内生成10000个输入值,用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")
ax = plt.gca() # 获取轴,默认有4个
# 隐藏两个轴,通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')
plt.show()
输出
2.在飞桨中,可以通过调用paddle.nn.functional.sigmoid和paddle.nn.functional.tanh实现对张量的Logistic和Tanh计算。在pytorch中找到相应函数并测试。
import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成10000个输入值,用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(z.tolist(), torch.sigmoid(z).tolist(), color='#ff0077', label="Logistic Function")
plt.plot(z.tolist(), torch.tanh(z).tolist(), color='#ff0077', linestyle ='--', label="Tanh Function")
ax = plt.gca() # 获取轴,默认有4个
# 隐藏两个轴,通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')
plt.show()
4.1.2.2 ReLU型函数
常见的ReLU函数有ReLU和带泄露的ReLU(Leaky ReLU)
ReLU(z)=max(0,z)
LeakyReLU(z)=max(0,z)+λmin(0,z)
其中λ为超参数。
1.使用python实现并可视化可视化“ReLU、带泄露的ReLU的函数”
import torch
import matplotlib.pyplot as plt
# ReLU
def relu(z):
return torch.maximum(z, torch.as_tensor(0.))
# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
# 当前版本torch暂不支持直接将bool类型转成int类型,因此调用了torch的cast函数来进行显式转换
a1 = (torch.can_cast((z > 0).dtype, torch.float32) * z)
a2 = (torch.can_cast((z <= 0).dtype, torch.float32) * (negative_slope * z))
return a1 + a2
# 在[-10,10]的范围内生成一系列的输入值,用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")
ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()
输出

2.在飞桨中,可以通过调用paddle.nn.functional.relu和paddle.nn.functional.leaky_relu完成ReLU与带泄露的ReLU的计算。在pytorch中找到相应函数并测试。
import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成一系列的输入值,用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(z.tolist(), torch.relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), torch.nn.LeakyReLU(0.1)(z), color="#f19ec2", linestyle="--", label="LeakyReLU Function")
ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()
输出
4.2 基于前馈神经网络的二分类任务
4.2.1 数据集构建
使用第3.1.1节中构建的二分类数据集:Moon1000数据集,其中训练集640条、验证集160条、测试集200条。该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到,每个样本包含2个特征。
from nndl.dataset import make_moons
# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])
输出
nndl.dataset.make_moons代码如下:
import torch
import math
import numpy as np
# 新增make_moons函数
def make_moons(n_samples=1000, shuffle=True, noise=None):
n_samples_out = n_samples // 2
n_samples_in = n_samples - n_samples_out
outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))
inner_circ_x = 1 - torch.cos(torch.linspace(0, math.pi, n_samples_in))
inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))
print('outer_circ_x.shape:', outer_circ_x.shape, 'outer_circ_y.shape:', outer_circ_y.shape)
print('inner_circ_x.shape:', inner_circ_x.shape, 'inner_circ_y.shape:', inner_circ_y.shape)
X = torch.stack(
[torch.cat([outer_circ_x, inner_circ_x]),
torch.cat([outer_circ_y, inner_circ_y])],
axis=1
)
print('after concat shape:', torch.cat([outer_circ_x, inner_circ_x]).shape)
print('X shape:', X.shape)
# 使用'torch. zeros'将第一类数据的标签全部设置为0
# 使用'torch. ones'将第一类数据的标签全部设置为1
y = torch.cat(
[torch.zeros([n_samples_out]), torch.ones([n_samples_in])]
)
print('y shape:', y.shape)
# 如果shuffle为True,将所有数据打乱
if shuffle:
# 使用'torch.randperm'生成一个数值在0到X.shape[0],随机排列的一维Tensor做索引值,用于打乱数据
idx = torch.randperm(X.shape[0])
X = X[idx]
y = y[idx]
# 如果noise不为None,则给特征值加入噪声
if noise is not None:
X += np.random.normal(0.0, noise, X.shape)
return X, y
4.2.2 模型构建
为了更高效的构建前馈神经网络,我们先定义每一层的算子,然后再通过算子组合构建整个前馈神经网络。
4.2.2.1 线性层算子
公式(4.8)对应一个线性层算子,权重参数采用默认的随机初始化,偏置采用默认的零初始化。代码实现如下:
from nndl.op import Op
# 实现线性层算子
class Linear(Op):
def __init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):
self.params = {}
# 初始化权重
self.params['W'] = weight_init([input_size, output_size])
self.params['W'] = torch.as_tensor(self.params['W'],dtype=torch.float32)
# 初始化偏置
self.params['b'] = bias_init([1, output_size])
self.inputs = None
self.name = name
def forward(self, inputs):
self.inputs = inputs
outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
return outputs
4.2.2.2 Logistic算子(激活函数)
本节我们采用Logistic函数来作为公式(4.9)中的激活函数。这里也将Logistic函数实现一个算子,代码实现如下:
class Logistic(Op):
def __init__(self):
self.inputs = None
self.outputs = None
def forward(self, inputs):
outputs = 1.0 / (1.0 + torch.exp(-inputs))
self.outputs = outputs
return outputs
4.2.2.3 层的串行组合
在定义了神经层的线性层算子和激活函数算子之后,我们可以不断交叉重复使用它们来构建一个多层的神经网络。实现一个两层的用于二分类任务的前馈神经网络,选用Logistic作为激活函数,可以利用上面实现的线性层和激活函数算子来组装。代码如下:
# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
def __init__(self, input_size, hidden_size, output_size):
"""
输入:
- input_size:输入维度
- hidden_size:隐藏层神经元数量
- output_size:输出维度
"""
self.fc1 = Linear(input_size, hidden_size, name="fc1")
self.act_fn1 = Logistic()
self.fc2 = Linear(hidden_size, output_size, name="fc2")
self.act_fn2 = Logistic()
def __call__(self, X):
return self.forward(X)
def forward(self, X):
"""
输入:
- X:shape=[N,input_size], N是样本数量
输出:
- a2:预测值,shape=[N,output_size]
"""
z1 = self.fc1(X)
a1 = self.act_fn1(z1)
z2 = self.fc2(a1)
a2 = self.act_fn2(z2)
return a2
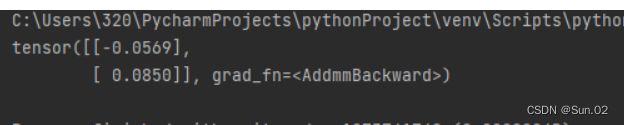
实例化一个两层的前馈网络,令其输入层维度为5,隐藏层维度为10,输出层维度为1。
并随机生成一条长度为5的数据输入两层神经网络,观察输出结果。
# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = torch.rand([1, 5])
result = model(X)
print ("result: ", result)
输出
result: tensor([[0.6000]])
Process finished with exit code 0
4.2.3 损失函数
# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(op.Op):
def __init__(self):
self.predicts = None
self.labels = None
self.num = None
def __call__(self, predicts, labels):
return self.forward(predicts, labels)
def forward(self, predicts, labels):
self.predicts = predicts
self.labels = labels
self.num = self.predicts.shape[0]
loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts)) + torch.matmul((1-self.labels.t()), torch.log(1-self.predicts)))
loss = torch.squeeze(loss, axis=1)
return loss
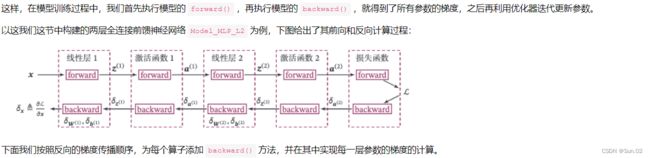
4.2.4 模型优化
神经网络的层数通常比较深,其梯度计算和上一章中的线性分类模型的不同的点在于:线性模型通常比较简单可以直接计算梯度,而神经网络相当于一个复合函数,需要利用链式法则进行反向传播来计算梯度。
4.2.4.1 反向传播算法
在上面实现算子的基础上,来实现误差反向传播算法。在上面的三个步骤中,
1.第1步是前向计算,可以利用算子的forward()方法来实现;
2.第2步是反向计算梯度,可以利用算子的backward()方法来实现;
3.第3步中的计算参数梯度也放到backward()中实现,更新参数放到另外的优化器中专门进行。
4.2.4.2 损失函数
实现损失函数的backward()
# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
def __init__(self, model):
self.predicts = None
self.labels = None
self.num = None
self.model = model
def __call__(self, predicts, labels):
return self.forward(predicts, labels)
def forward(self, predicts, labels):
self.predicts = predicts
self.labels = labels
self.num = self.predicts.shape[0]
loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
+ torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))
loss = torch.squeeze(loss, axis=1)
return loss
def backward(self):
# 计算损失函数对模型预测的导数
loss_grad_predicts = -1.0 * (self.labels / self.predicts -
(1 - self.labels) / (1 - self.predicts)) / self.num
# 梯度反向传播
self.model.backward(loss_grad_predicts)
4.2.4.3 Logistic算子
为Logistic算子增加反向函数
class Logistic(Op):
def __init__(self):
self.inputs = None
self.outputs = None
self.params = None
def forward(self, inputs):
outputs = 1.0 / (1.0 + torch.exp(-inputs))
self.outputs = outputs
return outputs
def backward(self, grads):
# 计算Logistic激活函数对输入的导数
outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
return torch.multiply(grads,outputs_grad_inputs)
4.2.4.4 线性层
代码如下
class Linear(Op):
def __init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):
self.params = {}
self.params['W'] = weight_init([input_size, output_size])
self.params['W'] = torch.as_tensor(self.params['W'],dtype=torch.float32)
self.params['b'] = bias_init([1, output_size])
self.inputs = None
self.grads = {}
self.name = name
def forward(self, inputs):
self.inputs = inputs
outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
return outputs
def backward(self, grads):
self.grads['W'] = torch.matmul(self.inputs.T, grads)
self.grads['b'] = torch.sum(grads, dim=0)
# 线性层输入的梯度
return torch.matmul(grads, self.params['W'].T)
4.2.4.5 整个网络
实现完整的两层神经网络的前向和反向计算
class Model_MLP_L2(Op):
def __init__(self, input_size, hidden_size, output_size):
# 线性层
self.fc1 = Linear(input_size, hidden_size, name="fc1")
# Logistic激活函数层
self.act_fn1 = Logistic()
self.fc2 = Linear(hidden_size, output_size, name="fc2")
self.act_fn2 = Logistic()
self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]
def __call__(self, X):
return self.forward(X)
# 前向计算
def forward(self, X):
z1 = self.fc1(X)
a1 = self.act_fn1(z1)
z2 = self.fc2(a1)
a2 = self.act_fn2(z2)
return a2
# 反向计算
def backward(self, loss_grad_a2):
loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
loss_grad_a1 = self.fc2.backward(loss_grad_z2)
loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
loss_grad_inputs = self.fc1.backward(loss_grad_z1)
4.2.4.6 优化器
在计算好神经网络参数的梯度之后,我们将梯度下降法中参数的更新过程实现在优化器中。与第3章中实现的梯度下降优化器SimpleBatchGD不同的是,此处的优化器需要遍历每层,对每层的参数分别做更新。
from nndl.opitimizer import Optimizer
class BatchGD(Optimizer):
def __init__(self, init_lr, model):
super(BatchGD, self).__init__(init_lr=init_lr, model=model)
def step(self):
# 参数更新
for layer in self.model.layers: # 遍历所有层
if isinstance(layer.params, dict):
for key in layer.params.keys():
layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]
nndl.opitimizer.Optimizer代码如下:
from abc import abstractmethod
#新增优化器基类
class Optimizer(object):
def __init__(self, init_lr, model):
#初始化学习率,用于参数更新的计算
self.init_lr = init_lr
#指定优化器需要优化的模型
self.model = model
@abstractmethod
def step(self):
pass
4.2.5 完善Runner类:RunnerV2_1
基于3.1.6实现的 RunnerV2 类主要针对比较简单的模型。而在本章中,模型由多个算子组合而成,通常比较复杂,因此本节继续完善并实现一个改进版: RunnerV2_1类,其主要加入的功能有:
- 支持自定义算子的梯度计算,在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度;
- 每层的模型保存和加载,将每一层的参数分别进行保存和加载。
class RunnerV2_1(object):
def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric
# 记录训练过程中的评估指标变化情况
self.train_scores = []
self.dev_scores = []
# 记录训练过程中的评价指标变化情况
self.train_loss = []
self.dev_loss = []
def train(self, train_set, dev_set, **kwargs):
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_epochs = kwargs.get("log_epochs", 100)
# 传入模型保存路径
save_dir = kwargs.get("save_dir", None)
# 记录全局最优指标
best_score = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
X, y = train_set
# 获取模型预测
logits = self.model(X)
# 计算交叉熵损失
trn_loss = self.loss_fn(logits, y) # return a tensor
self.train_loss.append(trn_loss.item())
# 计算评估指标
trn_score = self.metric(logits, y).item()
self.train_scores.append(trn_score)
self.loss_fn.backward()
# 参数更新
self.optimizer.step()
dev_score, dev_loss = self.evaluate(dev_set)
# 如果当前指标为最优指标,保存该模型
if dev_score > best_score:
print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
best_score = dev_score
if save_dir:
self.save_model(save_dir)
if log_epochs and epoch % log_epochs == 0:
print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
def evaluate(self, data_set):
X, y = data_set
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
self.dev_loss.append(loss)
# 计算评估指标
score = self.metric(logits, y).item()
self.dev_scores.append(score)
return score, loss
def predict(self, X):
return self.model(X)
def save_model(self, save_dir):
# 对模型每层参数分别进行保存,保存文件名称与该层名称相同
for layer in self.model.layers: # 遍历所有层
if isinstance(layer.params, dict):
torch.save(layer.params, os.path.join(save_dir, layer.name+".pdparams"))
def load_model(self, model_dir):
# 获取所有层参数名称和保存路径之间的对应关系
model_file_names = os.listdir(model_dir)
name_file_dict = {}
for file_name in model_file_names:
name = file_name.replace(".pdparams", "")
name_file_dict[name] = os.path.join(model_dir, file_name)
# 加载每层参数
for layer in self.model.layers: # 遍历所有层
if isinstance(layer.params, dict):
name = layer.name
file_path = name_file_dict[name]
layer.params = torch.load(file_path)
4.2.6 模型训练
使用训练集和验证集进行模型训练,共训练2000个epoch。评价指标为accuracy。
epoch_num = 1000
model_saved_dir = 'D:\project\DL\Lenet\logs'
# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1
# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)
# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)
# 评价方法
metric = accuracy
# 实例化RunnerV2_1类,并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)
输出
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.16875
[Train] epoch: 0/1000, loss: 0.7350932955741882
[Evaluate] best accuracy performence has been updated: 0.16875 --> 0.17500
[Evaluate] best accuracy performence has been updated: 0.17500 --> 0.18750
[Evaluate] best accuracy performence has been updated: 0.18750 --> 0.20000
[Evaluate] best accuracy performence has been updated: 0.20000 --> 0.21250
[Evaluate] best accuracy performence has been updated: 0.21250 --> 0.22500
[Evaluate] best accuracy performence has been updated: 0.22500 --> 0.25000
[Evaluate] best accuracy performence has been updated: 0.25000 --> 0.31250
[Evaluate] best accuracy performence has been updated: 0.31250 --> 0.37500
[Evaluate] best accuracy performence has been updated: 0.37500 --> 0.43750
[Evaluate] best accuracy performence has been updated: 0.43750 --> 0.46250
[Evaluate] best accuracy performence has been updated: 0.46250 --> 0.48125
[Evaluate] best accuracy performence has been updated: 0.48125 --> 0.49375
[Evaluate] best accuracy performence has been updated: 0.49375 --> 0.51250
[Evaluate] best accuracy performence has been updated: 0.51250 --> 0.55625
[Evaluate] best accuracy performence has been updated: 0.55625 --> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 --> 0.61875
[Evaluate] best accuracy performence has been updated: 0.61875 --> 0.63750
[Evaluate] best accuracy performence has been updated: 0.63750 --> 0.65000
[Evaluate] best accuracy performence has been updated: 0.65000 --> 0.66250
[Evaluate] best accuracy performence has been updated: 0.66250 --> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 --> 0.67500
[Evaluate] best accuracy performence has been updated: 0.67500 --> 0.68125
[Evaluate] best accuracy performence has been updated: 0.68125 --> 0.68750
[Evaluate] best accuracy performence has been updated: 0.68750 --> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.71875
[Train] epoch: 50/1000, loss: 0.664116382598877
[Evaluate] best accuracy performence has been updated: 0.71875 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73750
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.76250
[Evaluate] best accuracy performence has been updated: 0.76250 --> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80625
[Evaluate] best accuracy performence has been updated: 0.80625 --> 0.81250
[Train] epoch: 100/1000, loss: 0.5949881076812744
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Evaluate] best accuracy performence has been updated: 0.81875 --> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.83125
[Evaluate] best accuracy performence has been updated: 0.83125 --> 0.83750
[Train] epoch: 150/1000, loss: 0.5277273058891296
[Train] epoch: 200/1000, loss: 0.485870361328125
[Train] epoch: 250/1000, loss: 0.46499910950660706
[Train] epoch: 300/1000, loss: 0.4550503194332123
[Train] epoch: 350/1000, loss: 0.45022842288017273
[Train] epoch: 400/1000, loss: 0.44782382249832153
[Train] epoch: 450/1000, loss: 0.44659096002578735
[Evaluate] best accuracy performence has been updated: 0.83750 --> 0.84375
[Train] epoch: 500/1000, loss: 0.44594064354896545
[Evaluate] best accuracy performence has been updated: 0.84375 --> 0.85000
[Evaluate] best accuracy performence has been updated: 0.85000 --> 0.85625
[Train] epoch: 550/1000, loss: 0.44558531045913696
[Train] epoch: 600/1000, loss: 0.4453815519809723
[Evaluate] best accuracy performence has been updated: 0.85625 --> 0.86250
[Train] epoch: 650/1000, loss: 0.44525671005249023
[Train] epoch: 700/1000, loss: 0.4451737403869629
[Train] epoch: 750/1000, loss: 0.4451136589050293
[Train] epoch: 800/1000, loss: 0.4450666606426239
[Train] epoch: 850/1000, loss: 0.4450274407863617
[Train] epoch: 900/1000, loss: 0.4449935853481293
[Train] epoch: 950/1000, loss: 0.44496336579322815
把训练变成2000次后,运行结果如下:
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.21250
[Train] epoch: 0/2000, loss: 0.738420844078064
[Evaluate] best accuracy performence has been updated: 0.21250 --> 0.21875
[Evaluate] best accuracy performence has been updated: 0.21875 --> 0.23750
[Evaluate] best accuracy performence has been updated: 0.23750 --> 0.24375
[Evaluate] best accuracy performence has been updated: 0.24375 --> 0.26875
[Evaluate] best accuracy performence has been updated: 0.26875 --> 0.27500
[Evaluate] best accuracy performence has been updated: 0.27500 --> 0.28750
[Evaluate] best accuracy performence has been updated: 0.28750 --> 0.30000
[Evaluate] best accuracy performence has been updated: 0.30000 --> 0.31875
[Evaluate] best accuracy performence has been updated: 0.31875 --> 0.35625
[Evaluate] best accuracy performence has been updated: 0.35625 --> 0.37500
[Evaluate] best accuracy performence has been updated: 0.37500 --> 0.41250
[Evaluate] best accuracy performence has been updated: 0.41250 --> 0.43125
[Evaluate] best accuracy performence has been updated: 0.43125 --> 0.45000
[Evaluate] best accuracy performence has been updated: 0.45000 --> 0.46875
[Evaluate] best accuracy performence has been updated: 0.46875 --> 0.47500
[Evaluate] best accuracy performence has been updated: 0.47500 --> 0.49375
[Evaluate] best accuracy performence has been updated: 0.49375 --> 0.52500
[Evaluate] best accuracy performence has been updated: 0.52500 --> 0.58125
[Evaluate] best accuracy performence has been updated: 0.58125 --> 0.61875
[Evaluate] best accuracy performence has been updated: 0.61875 --> 0.66250
[Evaluate] best accuracy performence has been updated: 0.66250 --> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.71875
[Evaluate] best accuracy performence has been updated: 0.71875 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.73750
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.76875
[Train] epoch: 50/2000, loss: 0.6566254496574402
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.78750
[Evaluate] best accuracy performence has been updated: 0.78750 --> 0.79375
[Train] epoch: 100/2000, loss: 0.5740222334861755
[Train] epoch: 150/2000, loss: 0.49713021516799927
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80000
[Train] epoch: 200/2000, loss: 0.4507133662700653
[Train] epoch: 250/2000, loss: 0.426734060049057
[Train] epoch: 300/2000, loss: 0.41436272859573364
[Train] epoch: 350/2000, loss: 0.4077704846858978
[Train] epoch: 400/2000, loss: 0.4041588008403778
[Train] epoch: 450/2000, loss: 0.40213823318481445
[Train] epoch: 500/2000, loss: 0.40098461508750916
[Train] epoch: 550/2000, loss: 0.400308221578598
[Train] epoch: 600/2000, loss: 0.39989611506462097
[Train] epoch: 650/2000, loss: 0.39963141083717346
[Train] epoch: 700/2000, loss: 0.39944973587989807
[Train] epoch: 750/2000, loss: 0.39931559562683105
[Train] epoch: 800/2000, loss: 0.39920955896377563
[Train] epoch: 850/2000, loss: 0.39912062883377075
[Train] epoch: 900/2000, loss: 0.3990428149700165
[Train] epoch: 950/2000, loss: 0.3989725708961487
[Train] epoch: 1000/2000, loss: 0.3989078998565674
[Train] epoch: 1050/2000, loss: 0.39884766936302185
[Train] epoch: 1100/2000, loss: 0.39879104495048523
[Train] epoch: 1150/2000, loss: 0.39873751997947693
[Train] epoch: 1200/2000, loss: 0.39868679642677307
[Train] epoch: 1250/2000, loss: 0.39863845705986023
[Train] epoch: 1300/2000, loss: 0.39859244227409363
[Train] epoch: 1350/2000, loss: 0.3985483944416046
[Train] epoch: 1400/2000, loss: 0.398506224155426
[Train] epoch: 1450/2000, loss: 0.3984657824039459
[Train] epoch: 1500/2000, loss: 0.39842694997787476
[Train] epoch: 1550/2000, loss: 0.3983895480632782
[Train] epoch: 1600/2000, loss: 0.3983535170555115
[Train] epoch: 1650/2000, loss: 0.39831873774528503
[Train] epoch: 1700/2000, loss: 0.39828506112098694
[Train] epoch: 1750/2000, loss: 0.3982524871826172
[Train] epoch: 1800/2000, loss: 0.39822086691856384
[Train] epoch: 1850/2000, loss: 0.3981901705265045
[Train] epoch: 1900/2000, loss: 0.39816027879714966
[Train] epoch: 1950/2000, loss: 0.39813119173049927
可视化观察训练集与验证集的损失函数变化情况。
import matplotlib.pyplot as plt
# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.show()
#加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])
输出
4.2.7 性能评价
使用测试集对训练中的最优模型进行评价,观察模型的评价指标。
# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))
输出
[Test] score/loss:0.7900/0.4483
Process finished with exit code 0
从结果来看,模型在测试集上取得了较高的准确率。
下面对结果进行可视化:
import math
# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)
# 预测对应类别
y = runner.predict(x)
y = torch.squeeze((y>=0.5).to(dtype=torch.float32),axis=-1)
# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)
plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,axis=-1).tolist())
plt.show()输出
【思考题】对比
3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务谈谈自己的看法
Logistic Regression:典型的二值分类器,用来处理两类分类问题,当然,也可以用来处理多类问题。可以将Logistic Regression看做是仅含有一个神经元的单层的神经网络!神经网络可以看作是多个logistic回归构成的。而logistic回归似乎只能处理一个基本的线性可分问题。
总结
通过这次实验对前馈神经网络的基本概念、网络结构及代码实现等过程更加熟悉,并且对Logistic回归进行了回顾。
参考
NNDL 实验4(上) - HBU_DAVID - 博客园 (cnblogs.com)