PyTorch Autograd(backward grad 等PyTorch核心)
文章目录
-
- 绪论
- 1. PyTorch基础
- 2. 人工神经网络和反向传播
- 3. 动态计算图(dynamic computational graph)
- 4. 反向函数(Backward())
- 5. 数学:雅可比和向量
绪论
本人在学PyTorch,对它的计算图产生疑惑。后学习国外一篇博文后,感觉收获颇丰,故转载翻译而来。本文将会主要关注PyTorch计算图相关和autograd类的backward等方面。

 图1 它从不显式计算整个雅可比,它经常简化去直接计算JVP
图1 它从不显式计算整个雅可比,它经常简化去直接计算JVP
1. PyTorch基础
让我们不妨认为,当遇到大型人工神经网络时,我们使用微积分无能为力。通过显式地求解数学方程来计算如此大型的复合函数的梯度是不现实的,尤其因为这些曲线存在于高维空间,是不可能被理解的。
为了处理14维的超平面,可视化一个3-D的空间,然后大声对自己说14。每个人都这么做。——Geoffrey Hinton
这有了PyTorch的 autograd 的用武之地。它抽象了繁琐的数学知识,帮助我们有效地通过几行代码来计算高维曲线的梯度。
在深入探讨之前,我们需要知道一些基础的PyTorch概念。
(1)Tensor:简单地说,它只是PyTorch中的n维数组。Tensor支持一些额外的增强功能,使其独特:除了CPU,它可以被GPU加载,从而计算速度更高。设置.requires_grad = True,它(们)开始构建一个反向图(backward graph),通过使用动态计算图(dynamic computation graph,DCG,在本文后面会有介绍)追溯操作于在它(们)的每个操作(operation)来计算相关的梯度。
在PyTorch的早期版本中,类torch.autograd.Variable 是用来创建支持计算梯度和追溯操作的tensors,但是随着PyTorch v0.4.0 Variable 类被弃用,torch.Tensor和torch.autograd.Variable现在是相同的类。更准确地,torch.Tensor能够追溯历史操作,表现地和旧的Variable一样。
注:由于PyTorch的设计,只能计算浮点(floating point)tensor的梯度,所以在让它成为能够计算梯度的PyTorch tensor之前,我创建一个float的 numpy数组
#展示多种创建支持梯度tensor的方法
import torch
import numpy as np
x = torch.randn(2, 2, requires_grad = True)
# From numpy
x = np.array([1., 2., 3.]) #只有浮点型的张量才可以 require gradients
x = torch.from_numpy(x)
# Now enable gradient
x.requires_grad_(True)
# _ above makes the change in-place (its a common pytorch thing)
(2)Autograd:这个类是一个用来计算导数的工具(更准确地,雅可比向量积)。它记录了所有操作于可计算梯度的tensor上的操作,而且创建了一个称为动态计算图的无环图。该图的树叶是输入tensors,树根是输出tensors。通过从树根到树叶在图中追溯,和基于链式法则把每个梯度相乘来计算梯度。
2. 人工神经网络和反向传播
人工神经网络只不过是复合的数学函数,它被精心地调整来输出需要的结果。调整或者训练是通过一个被称为反向传播的好算法来实现的。反向传播是被用来计算损失(代价,loss)关于输入的权重(参数,weights)的梯度来更新权重,最终减小损失(loss)。
从某方面说,反向传播算法只是链式法则的花哨的名字。——Jeremy Howard
创建和训练一个人工神经网络包括下列的基本步骤:
(1)定义结构(architecture)
(2)使用输入的数据在结构上前向传播(forward propagate)
(3)计算损失
(4)反向传播计算出针对每个权重的梯度
(5)选择学习率(learning rate)来更新权重
在一个输入权重上的小小改变所引起的损失函数的改变被称作那个权重的梯度,而且它是使用反向传播来计算的。然后选择学习率和利用梯度来更新权重,以整体降低损失函数和训练神经网络。
这是以一种迭代的(iterative)方式完成的。在每次迭代中,一些梯度被计算得到,为了存储这些梯度函数一些计算图被建立。PyTorch通过建立动态计算图完成这个。该图是在每一次迭代中一点一点建立起来的,对梯度计算提供了最大的灵活性。比如,为了计算梯度,一个前向操作(函数)Mul,一个反向操作(函数)——MulBackward被动态地整合进入反向传播图
3. 动态计算图(dynamic computational graph)
支持梯度的tensor(variable)和函数(操作)结合起来创建动态计算图。因为数据流和应用于之上的操作是在运行时(runtime)被定义的,所以动态地构建相关计算图。这个图是被底层的autograd类动态创建的。你不需要在开始训练之前对所有可能的路径进行编码——你运行的就是你求导的。
一个简单的两个tensor的乘法的(multiplication)DCG如下所示:
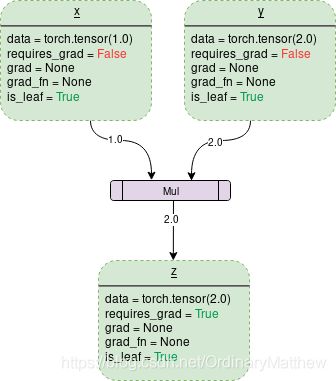
图中每个虚线框是一个变量variable,每个紫色矩形框是一个操作。每个variable对象都有一些成员,比如:
( 1) data:是一个variable所持有的数据。X持有一个1x1的tensor,值为1.0,y持有2.0 。z持有它们的乘积,即2.0 。
( 2) requires_grad: 这个成员,如果为 True,它会开始追溯所有的操作记录,和建立一个梯度计算的反向传播图。对一个任意的tnesor α ,它可以这样合适地操作: a.requires_grad_(True).
( 3) grad:grad持有梯度的值。如果 requires_grad是 False,它会持有一个 None值。即使 requires_grad为 True,它依旧持有一个 None值除非**.backward() 函数在其它节点(node)被调用了。比如,如果你为变量out调用了out.backward() ,而变量out 的计算与变量x 相关,进而x.grad将会持有∂out/∂x。
注:个人理解,因变量是用.backward,自变量用.grad,而且要因变量与自变量相关才能求出梯度。
(4) gard_fn: 这是用来计算梯度的反向函数(backward function)。
(5) is_leaf: 一个节点是树叶如果:
1) 它是被一些函数显式初始化的,比如 x= torch.tensor(1.0) 或者x = torch.randn(1, 1)
2) 它是在一些都有 requires_grad = False 的操作操作于tensor之后被创建的。
3) 它是通过对一些tensor调用. detach()方法创建的。
在调用. backward()时,梯度只填充于那些的 requires_grad , is_leaf 都为True的节点。 梯度是那些调用了.backward()输出节点关于其他叶子节点的。
在执行requires_grad = True时,PyTorch将会开始追溯操作,在每一步存储梯度函数。如下所示:
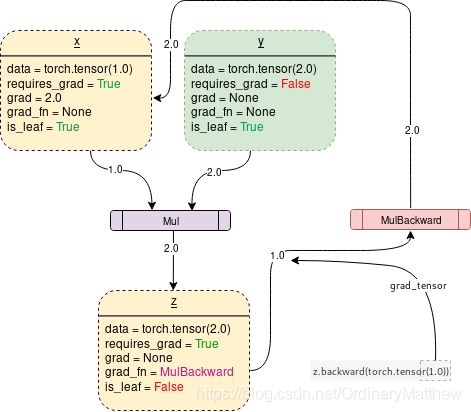
能够生成上述图片中信息的PyTorch 底层代码如下所示:
#在这个过程中,它不会显式地构造出整个雅可比矩阵。直接计算JVP通常更简单、更有效。
import torch
# 创建图
x = torch.tensor(1.0, requires_grad = True)
y = torch.tensor(2.0)
z = x * y
# 展示
for i, name in zip([x, y, z], "xyz"):
print(f"{name}\ndata: {i.data}\nrequires_grad: {i.requires_grad}\n\
grad: {i.grad}\ngrad_fn: {i.grad_fn}\nis_leaf: {i.is_leaf}\n")
为了让PyTorch从追溯历史和构建反向传播图中停止,代码可以被打包进with torch.no_grad():。它将会让代码运行更快无论何时梯度追溯不需要了。
import torch
# 创建图
x = torch.tensor(1.0, requires_grad = True)
# 检查追溯是否可行
print(x.requires_grad) #True
y = x * 2
print(y.requires_grad) #True
with torch.no_grad():
# 检查追溯是否可行
y = x * 2
print(y.requires_grad) #False
4. 反向函数(Backward())
反向函数是这样的,实际上它在反向图中从调用它的根tensor到根tensor可到达的叶子节点中的所有路径通过传递它的参数(默认是1x1的单元tensor)来计算梯度。被计算出来的梯度然后被存储在每个叶子节点的.grad中。
记住,反向图在前向传播(forward pass)的过程中已经被动态创建了。反向函数只需要使用已经被创建的图来计算梯度,并将它们存储在叶子节点中。
让我们分析下面的代码:
import torch
# 创建图
x = torch.tensor(1.0, requires_grad = True)
z = x ** 3
z.backward() #计算梯度
print(x.grad.data) #打印3: dz/dx
一件需要注意的重要事情是,当z.backward()被调用,一个tensor以z.backward(torch.tensor(1.0))被自动传递。torch.tensor(1.0)
是为了终止链式法则梯度乘法而提供的外部梯度。这个外部梯度以输入的形式传入MulBackward函数为了以后计算 x的梯度。传入.backward()的tensor的维度必须和正在被计算梯度的tensor的维度一致。比如,如果支持梯度的x和y如下:
x = torch.tensor([0.0, 2.0, 8.0], requires_grad = True)
y = torch.tensor([5.0 , 1.0 , 7.0], requires_grad = True)
而且 z = x * y
那么,为了计算z(1个1*3的tensor)关于x或者y的梯度,一个外部梯度需要以如下形式被传入 z.backward()函数:
z.backward(torch.FloatTensor([1.0, 1.0, 1.0])
注:z.backward()可能会抛出一个错误:
RuntimeError: grad can be implicitly created only for scalar outputs
传递给后向函数的tensor就像梯度的加权输出的权值一样。从数学上讲,这是向量乘以非标量张量的雅可比矩阵(本文将进一步讨论),因此它几乎总是一个单位张量(unit tensor),与向后调用的张量的维数相同,除非需要计算加权输出。
后向图(backward graph)图是在前向(forward)传递过程中由autograd类自动动态创建的。Backward()通过将其参数传递给已经生成的Backward图来计算梯度。
5. 数学:雅可比和向量
从数学上讲,autograd类只是一个雅可比向量积计算工具。简而言之,雅可比矩阵就是表示两个向量的所有可能偏导数的矩阵。它是一个向量相对于另一个向量的梯度。
注:在这个过程中,PyTorch从未显式地构造整个雅可比矩阵。直接计算JVP(雅可比向量积)通常更简单、更有效。
如果一个向量X = [x1, x2,…xn]用于计算其他向量f(X) = [f1, f2, …fn] 通过函数f,则雅可比矩阵(J)简单地包含了所有偏导数组合,如下所示:
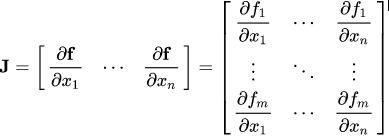
以上矩阵表示f(X)对X的梯度
设PyTorh支持梯度的tensor为
X = [x1, x2, …… xn](假设这是某个机器学习模型的权重)
X经过一些运算得到向量Y
Y = f(X) = [y1, y2, …. ym]
然后用Y来计算标量损失l。假设向量v恰好是标量损失l对向量Y的梯度,如下所示
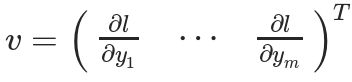 向量v被称为grad_tensor,并作为参数传递给backward()函数
向量v被称为grad_tensor,并作为参数传递给backward()函数
为了得到损失l对权值X的梯度,将雅可比矩阵J与向量v相乘
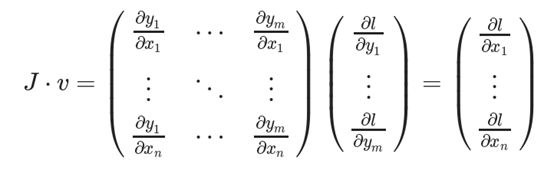 这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地提供外部梯度,即使是非标量输出。
这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地提供外部梯度,即使是非标量输出。
个人理解:X是权重向量,Y是假设函数(Hypothesis function,比如交叉熵或线性函数),l则是整体的损失函数(比如均方误差)。
目的是要计算l关于X的梯度,但是可能直接计算不太方便或者代价大或者存在其他弊端。所以采用先计算Y关于X的梯度,再计算l关于Y的梯度,再利用结果计算l关于X的梯度,这样做应该是有某些好处。