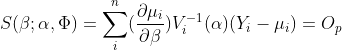广义估计方程GEE
本文大部分内容来源于书本和论文等资料,笔者将本文归为转载类,读者转载时请注明出处:https://blog.csdn.net/fjsd155/article/details/88318536
广义估计方程(generalized estimating equation, GEE)用于估计广义线性模型的参数(其中线性模型的结果之间可能存在未知的相关性)。于1986年由Liang和Zeger首次提出,是在广义线性模型和重复测量数据中,运用准似然估计方法估计参数的一种用于分析相关性数据的回归模型。
简介
对于观察值是连续性变量的重复测量资料,一般可以采用单变量方差分析(ANOVA)或多元方差分析(MANOVA)的方法(最好是连续性变量满足正态性、方差齐性以及各时间点组成的协方差具有球形性);但对于离散型重复测量资料(如变量为二分类变量),一般采用广义估计方程GEE进行统计分析。
单变量方差分析(单因素方差分析,ANOVA),就是传统的普通方差分析,将p个时间点类比成p个处理组(这种类比有些拗口),则对应为完全随机设计(总变异=处理变异+误差),可用于单组重复测量资料分析;若本身就存在多个处理组(多组重复测量资料),可再将m个处理组类比成m个区组(拗口的类比方式),则可采用随机区组的单因素方差分析设计(总变异=处理变异+区组变异+误差)。[ 注意:ANOVA要求p个处理组之间相互独立,因此要求满足球形检验(各时间点的测量值之间互相独立,或者称满足“独立结构”);若不满足球形检验,则需进行校正,否则容易增大第I类错误的风险 ]
多元方差分析(MANOVA),是将p个时间点看成p维向量,而不是看成一个时间变量的p个水平(不再将其类比为p个处理水平)。由于ANOVA要求的球形检验(各时间点测量值之间互相独立)前提,在很多情况下无法满足,而MANOVA不需要满足球形检验(正好适合处理存在相关性的问题,Hotelling's T2检验的拓展形式)。MANOVA的要求是服从多元正态分布。
这部分内容摘自《高级医学统计学》。
注意:重复测量资料,指的是结局变量是重复测量数据,而自变量(因素)是固有特性(分组、干预等等)。各时间点的测量值存在相关性也是针对结局变量而言。笔者模糊感觉,类似于重复测量的问题说不定也可用这类方法建模分析(可能需适当修改一下方法),如同时测量身高和体重作为结局变量,研究饮食、经济水平、运动状况等对结局变量的影响。
广义估计方程是在广义线性模型的基础上发展起来的, 专门用于处理纵向数据等重复测量资料的统计模型, 包括不均衡的纵向数据(纵向数据中研究对象重复测量次数、重复测量间隔时间可能有不同, 使得纵向数据不均衡, 如队列研究中途研究对象失访。而重复测量方差分析常需满足球形检验)。除了正态分布, GEE利用连接函数将二项分布、Poisson分布、Gamma分布等多种分布的应变量拟合为相应的统计模型, 解决了重复测量数据非独立性问题, 可得到稳健的参数。(本段摘自:顾刘金.应用广义估计方程分析纵向数据[J].预防医学,2018,30(01):106-107)
一般线性模型——局限性:只能拟合因变量服从正态分布的资料,不适用于分类资料。如果说方差分析做的事情本质上和线性回归一样,那么GEE做的事情本质上和广义线性回归是一样的(回归任务推广到分类任务)。
广义线性模型——广义估计方程是广义线性模型的延展。其借助线性模型的分析思路解决模型构造、参数估计和模型评价等一系列问题。广义线性模型要求有个均值函数![]() ,以便把因变量的期望值和线性预测值
,以便把因变量的期望值和线性预测值![]() 关联起来。基本结构为:
关联起来。基本结构为:![]() 。联接函数的作用就是对应变量作变换使之符合正态分布,变量变换的类型依应变量的分布不同而不同。优点:用于拟合应变量服从正态分布的模型,拟合服从二项分布、poisson分布、负二项分布的等指数分布族模型。通过指定不同的联接函数,把指数分布族的众多模型统一到一个模型框架中,具有极大的灵活性。
。联接函数的作用就是对应变量作变换使之符合正态分布,变量变换的类型依应变量的分布不同而不同。优点:用于拟合应变量服从正态分布的模型,拟合服从二项分布、poisson分布、负二项分布的等指数分布族模型。通过指定不同的联接函数,把指数分布族的众多模型统一到一个模型框架中,具有极大的灵活性。
广义估计方程处理重复测量纵向资料的优势:很好地解决了纵向数据的相关性问题,利用了纵向数据中每次测量的结果,大大减少了信息的损失。对于临床试验重复测量资料,广义估计方程能有效地考虑组内相关性,处理有缺失值的资料,可以获得中心效应的参数及其标准误的估计值。以及在考虑了中心效应之后,可以有效估计处理因素有无作用及其作用大小。采用广义估计方程对临床试验重复测量资料进行统计分析,可以使药物疗效评价更为客观。
作业相关矩阵
作业相关矩阵是广义估计方程中的一个重要概念,表示的是应变量的各次重复测量值两两之间相关性的大小。作业相关矩阵的形式常有以下几种:
(1)等相关,又称可交换的相关(exchangeable correla-tion),或复对称相关(compound symmetry correlation)。假设任意两次观测之间的相关是相等的。这种假设常用于不依时间顺序的重复测量资料。
(2)相邻相关,即只有相邻的两次观察值间有相关。
(3)自相关(autocorrelation),即相关与间隔次数有关,相隔次数越长,相关关系越小。
(4)不确定型相关(unstructured correlation),即不预先指定相关的形式,让模型根据资料特征自己估计。
(5)独立(independent),即不相关(uncorrelated),就是假设应变量之间不相关(多次观察值互相独立)。即独立结构或球形结构。
只要联接函数正确,总观测次数足够大,作业相关矩阵对参数估计的影响不大。
模型的基本构成
假设![]() 为第 i 个个体的第 j 次测量的变量(结果变量),
为第 i 个个体的第 j 次测量的变量(结果变量),![]()
协变量:![]() (比如处理因素(分组)就是一个协变量
(比如处理因素(分组)就是一个协变量![]() ;简单问题中往往只有一个自变量,如分组), 为对应于
;简单问题中往往只有一个自变量,如分组), 为对应于![]() 的p*1维解释变量向量。各观察对象间是独立的,但同一观察对象内的各次观察值间存在相关。
的p*1维解释变量向量。各观察对象间是独立的,但同一观察对象内的各次观察值间存在相关。
1. 建立结果变量与协变量之间的函数关系
指定![]() 的边际期望(marginal expectation)是协变量
的边际期望(marginal expectation)是协变量![]() 线性组合的已知函数。
线性组合的已知函数。
![]() ,
,![]()
式中: g(.)称为联接函数,通过它把yij的边际期望表达成协变量的线性组合; β=(β1…βp)为模型需要估计的参数向量。
2. 建立Yij的方差与平均值之间的函数关系
指定![]() 边际方差(marginal variance)是边际期望的已知函数。
边际方差(marginal variance)是边际期望的已知函数。
![]()
式中: V(.)为已知函数; Ф为尺度参数(scale parameter),表示Y的方差不能被![]() 解释的部分。这个参数也是需要模型估计的,对二项分布和Poisson分布而言, Ф=1。
解释的部分。这个参数也是需要模型估计的,对二项分布和Poisson分布而言, Ф=1。
3. 对![]() 构建一个P*P维作业相关矩阵
构建一个P*P维作业相关矩阵![]() , 用以表示因变量的各次重复测量值之间的相关性大小。
, 用以表示因变量的各次重复测量值之间的相关性大小。
4.求参数β的估计值及其协方差矩阵
令Ai是一个P*P维对角矩阵,其作业协方差矩阵为 ![]()
模型求解过程
(1) 假设重复测量值独立,按照广义线性模型计算出β,作为β的初始值,相当于普通最小二乘法估计。
(2) 基于标准化残差gij和假设的相关结构R,计算作业相关矩阵和作业协方差阵。
(3) 根据当前的作业协方差阵,修正β的估计。
(4) 重复(2)、(3)过程直至收敛。
广义估计方程的特点
(1)只要联接函数g(.)正确, 总观测次数足够大,即使作业相关矩阵Ri(α)指定不完全正确, β的可信区间和模型的其他统计量仍然渐近正确。
(2)广义估计方程采用准似然估计法估计参数,计算比最大似然法简单,并且对多元分布也没有要求,当样本量较大时, 甚至相关矩阵选择的不合适也对估计的影响不大。 特别是当资料中有缺失值,每个观测对象的观测次数不同,观察时间间隔不同等条件下,都可选用 GEE进行分析。
(3)广义估计方程应用条件较宽,可适用于多种类型的反应变量,如定量变量、分类变量、等级变量等,同时也可纳入多种类型的自变量,因而在重复测量设计资料统计分析中应用广泛。
一些思考
GEE 与LR 比较
- Logistic回归方程通常假定所有观察值是相互独立;
- 广义估计方程可输出作业相关矩阵,分析各时间点的相关参数,从而比较不同时间点的差异;
- 广义估计方程还可以探讨各因素的交互作用及对自变量作用的分解,即检验自变量对于不同时间点的影响大小是否相同。
至此,应该理解了重复测量资料为什么不能直接进行Logistic回归建模分析。
方差分析与回归的关系
那么,对于非重复测量资料,方差分析解决的问题,能否都采用回归建模进行解决呢?
之前已经知道,t 检验和线性回归是完全对应的。那么方差分析中情况如何呢?以下为个人看法,如有纰漏,烦请指教。
先看最简单的单因素方差分析,其实就是让处理效应(或分组因素,即所谓的单因素,对应于回归中的单个自变量)理解成多分类变量(3个处理组,理解为自变量X的3种取值),据此可以建立线性回归模型。但注意到,自变量不是连续性变量,而是分类变量(有时候为有序分类变量,大多时候为无序分类变量),有两种处理方式:一种是进行哑变量化,第二种是采用最优尺度回归(比哑变量法更有优势的处理技巧)。同样的,在多因素方差分析中,将各个因素转换成各个自变量,并进行最优尺度变换,可以建立线性回归。好像有这么个说法,方差分析其实就是线性回归的特例(所有自变量都是分类变量,并且都进行哑变量化),Wikipedia中有这么一句话:ANOVA is considered to be a special case of linear regression which in turn is a special case of the general linear model. 另外,对于R2这种指标,在ANOVA和线性回归中是等价的。
知乎上一个回答可以印证我的观点:方差分析和回归分析的异同是什么?
另外值得注意的是,还有个叫含协变量的方差分析(协方差分析),需与多因素方差分析进行区分(把影响观测值的其他变量当作协变量而不是“因素”,因为这个协变量是连续性变量,无法当成因素处理)。这种情况需先利用回归的方法(将“因素”和“协变量”一起作为自变量,以观测值作为结局变量,进行线性回归建模)消除组间不平衡的协变量的影响,再对校正后的因变量均数进行处理组间比较的方差分析(校正方法是采用回归模型截距进行校正)。
[ 注意用词:方差分析中的因素对应回归模型中的自变量,方差分析中的变量对应回归模型中的因变量。单因素单变量方差分析对应单自变量单因变量模型;多因素多变量方差分析对应多自变量多因变量模型 ]
如何理解协变量的校正 adjusted ?比如在Cox回归、LR中,如何理解对协变量进行了校正?
如何理解分层 stratified ?
若某变量(次要变量,一般为连续性变量或有序分类变量)与结局变量之间存在线性回归关系的,则该变量常被称为协变量,将其纳入考虑称为 adjusted;
若某变量(次要变量,一般为有序或无序分类变量)与结局变量之间关系不明确,但是其不同取值可能造成自变量与结局变量之间回归关系发生变化(不存在线性回归关系,但与主要自变量之间存在交互作用),则该变量常被称为分层变量,将其纳入考虑称为 stratified。有时候也会将协变量作为分层变量考虑。另外,RCT设计中的分层随机,所谓的分层因素其实有可能是协变量,我们此时也经常将其作为分层变量考虑。
在建模上的区别:协变量校正是先将自变量和协变量一起线性建模,然后用截距值对最终模型(因变量与主要自变量的模型)进行校正。分层分析是对于不同层分别进行建模(得到的系数值不同),如果分层变量和主要变量之间的交互作用弱,可以进一步对模型进行合并。
如何理解自变量与协变量?(摘自自变量与协变量)
自变量是指研究者主动操纵,而引起因变量发生变化的因素或条件,因此自变量被看作是因变量的原因。
协变量:在实验的设计中,协变量是一个独立变量(解释变量),不为实验者所操纵,但仍影响响应。同时,它指与因变量有线性相关并在探讨自变量与因变量关系时通过统计技术加以控制 的变量。常用的协变量包括因变量的前测分数、人口统计学指标以及与因变量明显不同的个人特征等。协变量应该属于控制变量的一种。有些控制变量可以通过实验操作加以控制(如照明、室温等),也称为无关变量;而另一些控制变量由于受实验设计等因素的限制,只能借助统计技术来加以控制,即成了统计分析中的协变量,因而属于统计概念。
如何理解交互作用与共线性?
交互作用是指两个变量共同作用对于结局变量的影响,不等于二者分别作用时的影响的加和(类似于生物学中的协同作用和拮抗作用)。对于交互作用明显的,可以采用分层的策略,分别建模,也可以添加交互项进行建模。
共线性是指两个或多个变量之间本来就存在线性相关关系(实际自由度小于表面上的自由度)。对于共线性明显的,可以先进行变量的筛选。
回归建模的最佳实践
1、回归应该关注“因果关系”,但是很多数据分析中忽略了这个内在逻辑。有的人把“果”当初因变量,把“因”当初自变量,这样随意建模时存在问题的,一般表现为建模效果不理想。根源在于,很多自变量共同作用导致了因变量,但是因变量和其他自变量共同作用难以导致某个自变量。因此有些大佬建模时会慎重考虑因果关系。
2、因果互相影响的情况。现实中,存在因变量对自变量也有影响的情况,比如“住院费越多,疗效越好;病人知道这个规律后,为了达到更好的疗效,而增加住院费”。这种情况可以采用两阶段最小二乘回归。
3、回归分析中普通最小二乘法有LINE要求,在违背这些情况时,有不同的应对策略。当自变量类型不满足要求时,可以采用最优尺度回归;当方差不齐时,可以考虑加权最小二乘回归;当自变量之间存在共线性时,可以考虑岭回归或LASSO回归。
GEE在R语言中,可以使用geepack、gee 或multgee等工具包进行分析。
拓展知识:趋势分析( trend analysis)
采用正交多项式( polynomial)分析某处理因素的均数随时间的变化情况正交多项式变换的对比方法:将两组资料转变为两条正交多项式曲线,检验这两条曲线参数是否来自同一总体。
① 首先检查最高阶次的参数在两对比组之间是否具有统计学意义。 ② 如果组间差异具有统计学意义,则可以认为包括本阶次及其余各阶次之间都具有不同的趋势。否则,应继续对次高阶次的参数作评价。 ③ 如果在任何阶次上差异都不具有统计学意义,说明这两条曲线的变化趋势是一致的。
Wikipedia中对GEE的描述:
GEEs belong to a class of regression techniques that are referred to as semiparametric because they rely on specification of only the first two moments. They are a popular alternative to the likelihood–based generalized linear mixed model which is more sensitive to variance structure specification. They are commonly used in large epidemiological studies, especially multi-site cohort studies, because they can handle many types of unmeasured dependence between outcomes.
Formulation部分也可以参考下其描述:Generalized estimating equation
重复测量资料分析方法的对比
1、ANOVA
当重复测量数据符合球形检验、各次测量数据分布满足正态分布时,可以采用ANONA。
2、MANOVA
重复测量数据对球形检验不做要求,但需满足多元正态分布。
相关介绍可参考高级统计学教材
R分析方法:基础包的manova()。
3、ASCA
ASCA全称是 ANOVA-simultaneous component analysis。该方法尚不了解,笔者估计也需要满足正态分布。据说可以分析主要趋势(结合了ANOVA和PCA的思想)。
可参考:
Bioinformatics 上的篇论文 ANOVA-Simultaneous component analysis (ASCA): a new tool for analyzing designed metabolomics data
Bioinformatics 上的篇论文 Discovering gene expression patterns in time course microarray experiments by ANOVA-SCA.
4、GEE
对数据分布和独立性不作要求(连接函数有多种可选,作业矩阵也有多种可选)。
R包:geepack、gee 或multgee等。
5、LMM 与 GLMM
LMM需各次测量数据分布满足正态分布,GLMM则对数据分布不作要求。
R包:lmm、glmm等。
可参考:广义线性混合模型GLMM
6、MEBA
MEBA全称为:Multivariate Empirical Bayes Analysis。虽然模型的假设是基于数据服从多元正态分布,但是MEBA的论文作者提到,只要是椭圆分布(elliptical distribution,简单理解就是多元分布的水平切面呈椭圆状,包括多元正态分布、Hotelling分布、Laplace分布等)就都有效。可以尝试下吧。
MEBA计算出每个变量的 MB-statistic 或 Hotelling T2-statistic(这里的Hotelling T2-statistic 严格来说是 ![]() -statistic,文献认为其作用与 MB-statistic 等价),并以此进行排序。
-statistic,文献认为其作用与 MB-statistic 等价),并以此进行排序。
MEBA使用方法:MEBA论文作者写了一个R包:timecourse(可通过 bioconductor 下载安装)。另外,MetaboAnalyst 也集成了MEBA。
注意timecourse包的使用方法,mb.long是用于单组或两组(包括配对)样本的时间序列分析(笔者注:Hotelling's T2的经验贝叶斯校正版,本质上还是Hotelling's T2),mb.MANOVA是用于多组样本的时间序列分析(笔者注:MANOVA的经验贝叶斯校正版,本质上还是MANOVA)。
笔者最开始没找到这个R包,幸亏根据关键字在Google里搜索到了这个网页:
https://rdrr.io/bioc/timecourse/man/mb.MANOVA.html
MEBA可参考:
Ann. Stat 上的一篇论文A multivariate empirical Bayes statistic for replicated microarray time course data.
Bioinformatics 上的篇论文 MetATT: a web-based metabolomics tool for analyzing time-series and two-factor datasets
(MetATT 就是 MetaboAnalyst 的前身,是Xia Lab(Jianguo Xia 教授团队)开发的工具,集成了ASCA 和 MEBA,在此之前仅有MATLAB中有MEBA的工具包)
关于模型的分析效能,一般要求越严格的方法,其分析效能越高(适用范围和分析效能很难兼得)。
惩罚广义估计方程(pGEE)
本部分参考自:曹红艳,曾平,李治, 等.惩罚广义估计方程在纵向数据基因关联分析中的应用[J].中国卫生统计,2017,34(4):534-537.
Wang等人2012年在论文Penalized Generalized Estimating Equations for High‐Dimensional Longitudinal Data Analysis中提出了pGEE的方法,将GEE推广到了高维数据分析中。
Oracle性质:一个好的惩罚函数估计值应具备无偏性、稀疏性和连续性,即Oracle性质。
SCAD惩罚能保留较大的系数,同时将较小的系数收缩为0,具有Oracle性质。其惩罚函数的导数如下:
![]() ,其中,I为指示函数,a为预先选择的常数(往往推荐a=3.7)。
,其中,I为指示函数,a为预先选择的常数(往往推荐a=3.7)。
对GEE的得分函数进行SCAD惩罚,得到pGEE的惩罚表达式为:
![]() ,
,
其中:
采用minofization-maximization算法和Newton-Raphson算法进行简化和迭代,可以计算出pGEE的参数估计值。pGEE估计值依赖于惩罚参数λ,因此往往采用交叉验证(cross validation,CV)选择最优λ。
最终的建模,可以根据AIC或BIC等进行变量选择。
对于这类问题,还可以使用基于Lasso的LMM(linear mixed model)或基于SCAD的LMM对结果进行验证和比较(都可以尝试下),之后有空可以总结下高通量纵向数据的统计分析方法。
pGEE在R语言中,可以使用PGEE这个包进行分析。
注意:pGEE的适用场景需注意,重复测量的指标是唯一的,比如动态体重,这将作为因变量,而不可以将需要筛选的特征作为重复测量的变量(比如代谢物等),也就是说,需要筛选的特征是不随时间变化的特征。因此pGEE不适用于纵向代谢组学筛选代谢物的情形。
另外,GEE和GMM广义矩方法之间存在密切的关系。详情请参考:广义矩方法(GMM)和广义估计方程(GEE)到底有什么区别
本文章虽注明为转载,但其实是整合统计书和几篇论文的内容所得,原出处请参考如下参考文献。
参考文献
万崇华等. 高级医学统计学. 科学出版社.
李雪原,张雪雷,仇丽霞.广义估计方程处理重复测量数据的参数解释[J].中国药物与临床,2015,(2):167-170.
顾刘金.应用广义估计方程分析纵向数据[J].预防医学,2018,30(01):106-107
田小龙,陈圆圆,朱笑笑,胡静静,赵文娟.广义估计方程[PPT]
Wikipedia: Generalized estimating equation
Wang, L. , Zhou, J. and Qu, A. (2012), Penalized Generalized Estimating Equations for High‐Dimensional Longitudinal Data Analysis. Biometrics, 68: 353-360.
曹红艳,曾平,李治, 等.惩罚广义估计方程在纵向数据基因关联分析中的应用[J].中国卫生统计,2017,34(4):534-537.
广义矩方法(GMM)和广义估计方程(GEE)到底有什么区别
Tai, Y. C. & Speed, T. P. A multivariate empirical Bayes statistic for replicated microarray time course data. Ann. Stat. 34, 2387–2412, 10.1214/009053606000000759 (2006).
Smilde AK, et al. ANOVA-Simultaneous component analysis (ASCA): a new tool for analyzing designed metabolomics data, Bioinformatics , 2005, vol. 21
Nueda, M. J. et al. Discovering gene expression patterns in time course microarray experiments by ANOVA-SCA. Bioinformatics 23, 1792–1800, 10.1093/bioinformatics/btm251 (2007).