蓝桥杯刷题日记 更新到2022/2/5
蓝桥杯刷题日记
文章目录
- 蓝桥杯刷题日记
-
- DAY1
-
- 1、递归实现指数型枚举
- 2、递归实现组合型枚举
- 3、递归实现排列型枚举
- Day2
-
- 1、八皇后问题
- *2、费解的开关
- 3、带分数
- Day3
-
- 1、飞行员兄弟
- 2、翻硬币
- DAY4(二分和前缀和)
-
- 1、数的范围
- 2、数的三次方根
- DAY5
-
- 1、机器人跳跃问题
- 2、四平方和
- DAY6
-
- 1、分巧克力
- Day7
-
- 1、激光炸弹(前缀和)
- 2、K倍区间
- 3、买不到的数目
- DAY8
-
- 1、蚂蚁感冒
- 2、饮料换购
- 3、 01背包
- 4、摘花生
- DAY9
-
- 1、错误票据
- 2、剪格子
- DAY10
-
- *1、大臣的旅费(树形dp)
- DAY11
-
- 1、最长上升子序列
- 2、连号区间数
- *3、地宫取宝
- DAY12
-
- 1、快速幂
- 2、64位快速乘法
- 3、波动数列
- DAY13
-
- *1、小朋友排队
- 2、垒骰子
- DAY14
-
- 1、生命之树
- 2、密码脱落
- DAY15(枚举)
-
- 1、特殊密码锁
- 2、拨钟问题
- DAY16(递归)
-
- 1、全排列问题
- 2、2的幂次方表示
- Day17(递归)
-
- 1、表达式问题
- 2、简单数的划分
- DAY18(动态规划1)
-
- 1、拦截导弹
- 2、Zipper
DAY1
1、递归实现指数型枚举
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zjG8RpKt-1644049163720)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220110145030958.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mVadPAaE-1644049163721)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220110145332484.png)]
图抄网上的,思路很简单(但是竟然不会做,只能说数据结构全部还给王丽萍了),每一个数选择是一种情况,不选择是一种情况,所以只需要每个数标记选择和不选择进行递归就可以了。
#include
#include
using namespace std;
int n;
bool flag[16];
void rec(int v)
{
if(v>n)
{
for(int i=1;i<=n;i++)
if(flag[i]) cout<>n;
rec(1);
return 0;
}
2、递归实现组合型枚举
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kLV88ogW-1644049163722)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220110152643697.png)]
还是递归题,参考上题的思路,我们只需要flag里有m个状态为1的时候也返回就可以了(flag里有m个返回要在v>n之前返回,我真是笨蛋)
然后递归多加1个参数来记录有多少个已经被标记为1了就可以了。
这个是自己写的代码:
#include
#include
using namespace std;
int n,m;
bool flag[16];
void rec(int v,int num)
{
if(num==m)
{
for(int i=1;i<=n;i++)
if(flag[i]) cout<n) return;
flag[v]=true;
rec(v+1,num+1);
flag[v]=false;
rec(v+1,num);
}
int main(){
cin>>n>>m;
rec(1,0);
return 0;
}
别人写的代码,我先看看思路:
#include
using namespace std;
const int N = 30;
int n, m;
int path[N];
bool st[N];
void dfs(int u, int start)
{
if (u > m)
{
for (int i = 1; i <= m; i++)
cout << path[i] << " ";
cout << endl;
return;
}
for (int i = start; i <= n; i++)
{
if(!st[i])
{
st[i] = true;
path[u] = i;
dfs(u + 1, i);
st[i] = false;
}
}
}
int main()
{
cin >> n >> m;
dfs(1, 1);
return 0;
}
其实思路差不多,只不过他的第二个参数标记成开始的位置,所以其实也差不了多少,不过确实
3、递归实现排列型枚举
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2gOfWlSa-1644049163722)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220111091137678.png)]
王丽萍讲过的题,每一次选取一个数,然后这个数不能再次选择,并且记录到数组里去,到最后将所有的数都选择完了,输出这个数组,并且将状态回溯到之前没选择这个数的状态,选择下一个数。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lCb8cTbQ-1644049163722)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220111091335113.png)]
#include
#include
using namespace std;
int n;
bool flag[20];
int record[20];
void rec(int v)
{
if(v>n)
{
for(int i=1;i<=n;i++)
cout<>n;
rec(1);
return 0;
}
Day2
1、八皇后问题
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XjSECIIA-1644049163722)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220111091515395.png)]
王丽萍绝对讲过原题了,做的时候又尬住了,满脑子想的就是当时好像说要用三个bool数组牺牲空间复杂度来简化时间复杂度,三个数组分别标记列、右上斜线和右下斜线。
还是把回溯法 :先放然后递归然后还原原状态的这个关键点忘记了,只要想起来回溯大概是怎么回溯的实际上很快就做的出来。
#include
#include
using namespace std;
int n;
char map[10][10];
bool col[10];
bool rg_down[19];
bool rg_up[19];
void rec(int v)
{
if(v==n)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cout<>n;
for(int i=0;i<10;i++)
{
for(int j=0;j<10;j++)
map[i][j]='.';
}
rec(0);
return 0;
}
*2、费解的开关
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KYrUjjIl-1644049163723)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220111094102026.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ItTYmvNo-1644049163723)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220111094139993.png)]
这题其实从昨天开始就开始想了,看了答案一开始还没看懂,当时说"枚举第一行开灯的所有情况",我真的是大大的?,后来去搜了份题解才知道,要使第一行不开的灯打开,必须要让正下方的第二行的灯改变状态,直到最后一行查看是否全为绿色,最后得到最小的次数。
确实还是太菜了,尝试一下自己写写看看有什么问题没有。
很奇怪真的太奇怪了,为什么先把灯关了递归和先开了递归得到的结果不一样,真的是匪夷所思,之后可能再看看才能知道。
思路基本上就是先把第一行的所有情况遍历一遍,然后通过check方法判断这个情况是否可行。
check方法其实就是第一行为关灯的话那么把第二行正下方的灯转变状态,然后上面的灯就开。之后第三行在变化让第二行全1………一直到第4行,把第四行全变完直接查看第五行的状态就行了,每一次都计数,这样的话就可以得到最后的次数。
自己写的代码:
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
int map[7][7];
int back[7][7];
int dx[5]={0,-1,0,1,0};
int dy[5]={0,0,1,0,-1};
int ans;
int check(int k)
{
memcpy(back,map,sizeof(map));
for(int i=1;i<=4;i++)
for(int j=1;j<=5;j++)
{
if(!back[i][j])
{
k++;
for(int m=0;m<5;m++)
back[i+1+dx[m]][j+dy[m]]=!back[i+1+dx[m]][j+dy[m]];
}
}
for(int i=1;i<=5;i++)
if(!back[5][i]) return INF;
return k;
}
void dfs(int cnt,int k)//枚举第一行所有情况
{
if(cnt>5)
{
ans=min(ans,check(k));
return;
}
for(int i=0;i<5;i++)
map[1+dx[i]][cnt+dy[i]]=!map[1+dx[i]][cnt+dy[i]];
dfs(cnt+1,k+1);//按这个开关
for(int i=0;i<5;i++)
map[1+dx[i]][cnt+dy[i]]=!map[1+dx[i]][cnt+dy[i]];
dfs(cnt+1,k);//不按这个开关
}
int main()
{
int n;
cin>>n;
for(int m=0;m 别人的代码:
#include
using namespace std;
const int N = 6;
const int INF = 0x3f3f3f3f;
int dx[N] = { -1,0,1,0,0 }, dy[N] = { 0,1,0,-1,0 };
char g[N][N], backup[N][N];
int n;
void turn(int x, int y)//将g[x][y]的状态进行改变
{
for (int i = 0; i < 5; i++)
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= 5 || b < 0 || b >= 5)continue;
g[a][b] ^= 1;
}
}
int main()
{
cin >> n;
while (n--)
{
for (int i = 0; i < 5; i++)cin >> g[i];//直接读一行用位运算
int res = INF;
for (int op = 0; op < 1 << 5; op++)
{
memcpy(backup, g, sizeof g);
int step = 0;
for (int i = 0; i < 5; i++)//第一行变化
{
if (op >> i & 1)
{
step++;
turn(0, i);
}
}
for (int i = 0; i < 4; i++)//check函数
{
for (int j = 0; j < 5; j++)
{
if (g[i][j] == '0')
{
step++;
turn(i + 1, j);
}
}
}
bool is_dark = false;
for (int j = 0; j < 5; j++)
{
if (g[4][j] == '0')
{
is_dark = true;
break;
}
}
if (!is_dark)res = min(res, step);
memcpy(g, backup, sizeof backup);
}
if (res > 6)res = -1;
cout << res << endl;
}
return 0;
}
3、带分数
这个题应该是比较难的,反正我看答案了
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZQeMGGat-1644049163723)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220112160017161.png)]
但是仔细一想其实假设我知道了要用递归做这题肯定很简单啊,因为其实假设要用递归做了,那么就只能递归构造数字,这个题有三个数字要构造,那么先递归构造第一个,再第一个基础上递归构造两个,然后最后拿两个算第三个,第三个如果满足要求的话就说明是对的,就算做一种。麻烦的点在于要写两个递归函数。
#include
#include
#include
using namespace std;
long long n,len,ans;
bool flag[10],back[10];
bool check(long long a,long long c)
{
long long b= (n-a)*c;
if(!b||!a||!c) return false;
memcpy(back,flag,sizeof(flag));
for(;b;b/=10)
{
int tmp=b%10;
if(!tmp||back[tmp]) return false;
back[tmp]=true;
}
for(int i=1;i<=9;i++)
if(!back[i]) return false;
return true;
}
void dfs_c(int u,int a,int c)
{
if(u>=10) return;
if(check(a,c)) ans++;
for(int i=1;i<=9;i++)
{
if(!flag[i])
{
flag[i]=true;
dfs_c(u+1,a,c*10+i);
flag[i]=false;
}
}
}
void dfs_a(int u,int a)
{
if(a>=n)return;
if(u>=10) return;
if(a) dfs_c(u,a,0);
for(int i=1;i<=9;i++)
{
if(!flag[i])
{
flag[i]=true;
dfs_a(u+1,a*10+i);
flag[i]=false;
}
}
}
int main()
{
cin>>n;
len=0;
for(long long tmp=n;tmp;tmp/=10)
len++;
dfs_a(0,0);
cout< Day3
1、飞行员兄弟
这两天去练车了真的挺累的,没怎么写,明天估计还得忙双创,测核酸,哎,这题看了就不会,想了半天了,最后还是抄的答案,
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VgzZ9z6X-1644049163723)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220114233112578.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4XzNXzJX-1644049163724)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220114233123512.png)]
一直想着怎么用DFS把这个题搜索出来,想着和费解的开关差不多一样来做,但是确实没有找到递推的关系,也没想到最后答案用暴力的做法直接把答案全部枚举出来2^16次方根本每办法递归,所以就用了很巧的位运算来记录每一个开关需要变化的关联开关,然后全部遍历一遍,得出答案。(因为这个题最大的变化开关数为16次,如果相同的开关变化两次,那么就相当于没有任何变化)
/*
基本抄的
*/
#include
#include
#include
#include
#include
#define N 4
#define INF 100
using namespace std;
typedef pair PII;
int change[N][N];
int get(int x,int y)
{
return x*N+y;
}
int main()
{
for(int i=0;i>line;
for(int j=0;jpath;
for(int i=0;i<1<<16;i++)
{
int now=state;
vector tmp;
for(int j=0;j<16;j++)
{
if(i>>j&1)
{
int x=j/4;
int y=j%4;
now^=change[x][y];
tmp.push_back({x,y});
}
if(!now&&(path.empty()||path.size()>tmp.size()))
path=tmp;
}
}
cout< 2、翻硬币
1208. 翻硬币 - AcWing题库
很晚了QAQ,12:00想不出来就睡了,
//第二天
果然休息好做题也快,这题没什么难度,不知道为什么把它列在搜索里,就遍历一遍字符串比比他们哪里不一样,用滑动窗口一下就做出来了
自己写的代码:
#include
#include
#include
#include
#include
using namespace std;
string a;
string b;
int main()
{
cin>>a>>b;
int st=0,end=0,ans=0;
int len=a.size();
for(;st 别人的代码也差不多
DAY4(二分和前缀和)
1、数的范围
789. 数的范围 - AcWing题库
啊这题,耍赖皮拿upper_bound和lower_bound()做出来了,其实这种升序的题一看就知道应该要拿二分什么之类的做
自己写的依靠库函数的代码:
#include
#include
#include
#include
#include
using namespace std;
int n,m;
vector v;
int main()
{
cin>>n>>m;
for(int i=0;i>tmp;
v.push_back(tmp);
}
for(int i=0;i>tmp;
vector::iterator start=lower_bound(v.begin(),v.end(),tmp);
vector::iterator end=upper_bound(v.begin(),v.end(),tmp);
int x=-1,y=-1;
if(start!=v.end()&&*start==tmp)
x=start-v.begin();
if(x!=-1)
y=end-v.begin()-1;
cout< 别人自己写的二分:
#include
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, m;
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)cin >> a[i];
while (m--)
{
int x;
cin >> x;
int l = 0, r = n - 1;
while (l < r)//第一次二分确定开端
{
int mid = l + r >> 1;//(除2写的好花哨)
if (a[mid] >= x)r = mid;
else l = mid + 1;
}
if (a[l] != x)
cout << -1 << ' ' << -1 << endl;
else//如果找到的话就第二次二分搜索,
{
cout << l << ' ';
l = 0, r = n - 1;
while(l> 1;
if (a[mid] <= x)l = mid;
else r = mid - 1;
}
cout << r << endl;
}
}
return 0;
}
2、数的三次方根
没什么好说的,范围给出了,所以可以2分搜索是否满足条件
#include
#include
#include
#include
#include
#include
#include
using namespace std;
double get(double x)
{
return x*x*x;
}
int main()
{
double st,end,n,mid;
cin>>n;
st=-10000.0;
end=10000.0;
while(end-st>=1e-7)
{
mid=(st+end)/2.0;
if(get(mid)>=n)
end=mid;
else
st=mid;
}
printf("%.6lf",st);
return 0;
}
DAY5
1、机器人跳跃问题
730. 机器人跳跃问题 - AcWing题库
总的来说和原来程序设计的轻功水上漂差不多就是二分搜索判断它是不是可以
写的过程中没有注意到一个问题就是,假设我的mid很大,带到check函数里,我每次都要吧能量值翻倍,这样的话mid就会越界,所以当能量大于1e5的时候就直接返回true,因为这时候所有的能量值都比h[i]要大。
#include
#include
#include
#include
#include
#include
#include
using namespace std;
vector v;
vector::iterator it;
int n,l,r,mid;
bool check(int e)
{
for(it=v.begin();it!=v.end();it++)
{
if(e<*it)
e-=*it-e;
else
e+=e-*it;
if(e<0)
return false;
if(e>=1e5)
return true;
}
return true;
}
int main()
{
cin>>n;
for(int i=0;i>tmp;
v.push_back(tmp);
}
l=1;
r=100000;
while(l 2、四平方和
这题真的是,本来应该是1/17(DAY5)的题了,结果拖到1/18才搞定
这题理论上不应该是二分的,我一开始的想法肯定是暴力枚举,但是枚举肯定不行,它题目要求是联合主键的排序第一个,我的想法是除去前三个以外最后一个二分排序O(n3logn),他最大的5*106,超了
刷题单的答案给了2分搜索,他的思路我不是很能理解,把所有的c和d枚举,然后因为a、b的组合和c和d组合是对称的,所有枚举出来的c和d也包含了a和b的取值,那么就定好a和b以后2分搜索c和d就感觉也是O(n^3logn)不懂,可能顺序搜a和b比搜c和d快,所以就可以做出来
二分的代码:
#include
using namespace std;
const int N = 2500010;
struct sum
{
int s, c, d;
bool operator<(const sum& t)const
{
if (s != t.s)return s < t.s;
if (c != t.c)return c < t.c;
return d < t.d;
}
}sum[N];
int n, m;
int main()
{
cin >> n;
for (int c = 0; c * c <= n; c++)
for (int d = c; c * c + d * d <= n; d++)
sum[m++] = { c * c + d * d,c,d };
sort(sum, sum + m);
for(int a = 0; a * a <= n; a++)
for (int b = 0; a * a + b * b <= n; b++)
{
int t = n - a * a - b * b;
int l = 0, r = m - 1;
while (l < r)
{
int mid = l + r >> 1;
if (sum[mid].s >= t)r = mid;
else l = mid + 1;
}
if (sum[l].s == t)
{
cout << a << ' ' << b << ' ' << sum[l].c << ' ' << sum[l].d << endl;
return 0;
}
}
return 0;
}
网页上的解析就是枚举+哈希:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V56zWJ5w-1644049163724)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220118162311106.png)]
说实话比二分肯定快,估计空间也差不了太多但是想不到(我觉得绝对是比二分好理解的)
代码:
#include
#include
using namespace std;
const int N = 1e8 + 10;
int h[N];
int main() {
int n;
cin >> n;
//打表,找出1 - n,所有完全平方数两两之和,如果存在只记第一次出现(题目要求找出字典序小的)
for (int i = 0; i * i * 2<= n; i++) {
for (int j = i; j * j + i * i <= n; j++) {
if (!h[i * i + j * j])
h[i * i + j * j] = i + 1;//防止i = 0时在后面判断查找跳过 i = 0的情况
}
}
//0<= a <= b <= c <= d,可以得出a^2 <= n / 4, a^2 + b^ 2 <= n / 2;
for (int i = 0; i * i * 4 <= n; i++) {
for (int j = i; j * j + i * i <= n / 2; j++) {
int t = n - i * i - j * j;
if (h[t]) {
int c = h[t] - 1;
//防止开根号后因为精度关系,向下取整,例:25 开根号得到4.99999向下取整为4;
int d = (sqrt(t - c * c) + 1e-4);
printf("%d %d %d %d", i, j, c, d);
return 0;
}
}
}
return 0;
}
DAY6
1、分巧克力
这题一看就有思路了,明显的二分搜索,在题目给的范围内判断边长能不能符合条件
就是假设每一条巧克力长a[i]宽b[i],分成k*k的正方形,那么总的个数就是(a[i]/k)**(b[i]/k)的总和,那只要二分搜索k就可以了
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef pairPII;
const int N=1e5;
int n,m,l,r;
vector v;
bool check(int k)
{
int sum=0;
for(int i=0;i=m) return true;
return false;
}
int main()
{
cin>>n>>m;
for(int i=0;i>a>>b;
v.push_back({a,b});
}
l=1,r=N;
while(l Day7
1、激光炸弹(前缀和)
99. 激光炸弹 - AcWing题库
前缀和就是尺取法
就比如
a[1],a[2],a[3]……………………………………a[n];
那么s[1],s[2]…………………………s[n]就表示从a[i]加到a[i],可以o[1]的算出a[i]加到a[j] (s[j]-s[i]);
二维的也是一样,
这个题就是典型的二维前缀和问题:
代码如下:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=5010;
int g[N][N];
int n,r;
int main()
{
cin>>n>>r;
r=min(r,5001);
int s=r,m=r;
for(int i=0;i>x>>y>>w;
x++;y++;
s=max(s,x);
m=max(m,y);
g[x][y]+=w;
}
for(int i=1;i<=s;i++)
for(int j=1;j<=m;j++)
g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
int res=0;
for(int i=r;i<=s;i++)
for(int j=r;j<=m;j++)
res=max(res,g[i][j]-g[i-r][j]-g[i][j-r]+g[i-r][j-r]);
cout< 2、K倍区间
1230. K倍区间 - AcWing题库
这道题……真的无语
我看着觉得挺简单的,结果还是没做出来;
我知道要用前缀和,但是假设除了前缀和其他什么都不用,就可以想想,我要定左边界i和右边界j利用s[j]-s[i-1]%k==0才能判断,那么这样的话i和j都要循环就变成了O(n^2)了,题目要求数据最大1e5,所以不行。
要提高效率只能牺牲空间,那这时候应该想到用哈希。问题是哈希怎么做?
抄答案:
这样的话我只需要再开一个数组cnt[N]即可,cnt[x]表示有多少个s[i]%k==x,这样的话时间复杂度就提高到了
想到这还是会寄,因为cnt[0]起始值是1:
哭了。所以最后还是抄完了答案:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=100010;
ll a[N];
int cnt[N];
ll n,k;
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
int w;
cin>>w;
a[i]=a[i-1]+w;
}
ll res=0;
cnt[0]++;
for(int i=1;i<=n;i++)
{
res+=cnt[a[i]%k];
cnt[a[i]%k]++;
}
cout< 3、买不到的数目
1205. 买不到的数目 - AcWing题库
蓝桥赛A组原题,冲!
这题满脑子想的都是dp,就硬算……,因为dp[i]表示i能不能满足条件,那么dp[i]=dp[i-n]+dp[i-m];在注意一下特殊的情况然后遍历一遍肯定是能过的,代码如下:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=1000010;
int a[N];
int n,m;
int main()
{
cin>>n>>m;
if(n>m)
{
int tmp=n;
n=m;
m=tmp;
}
a[0]=1;
a[n]=1;
int ans=n-1;
for(int i=n+1;i 但是,额,标答用数学方法直接算出来了,我大无语……
(36条消息) 数论系列 求证:设自然数a,b互质,则不能表示成ax+by(x,y为非负整数)的最大整数是ab-a-b_未来AI-CSDN博客
代码:
#include
using namespace std;
int main()
{
int p, q;
cin >> p >> q;
cout << (p - 1) * (q - 1) - 1 << endl;
return 0;
}
DAY8
1、蚂蚁感冒
1211. 蚂蚁感冒 - AcWing题库
这道题其实就是看蚂蚁相遇了多少次
1、最简单的情况:第一只向左,没有蚂蚁向右,则没有蚂蚁再感染,同理第一只蚂蚁向右,没有蚂蚁向左,也没有蚂蚁感染
2、复杂的情况就是,如果第一只蚂蚁向左,有蚂蚁在左边向右在左边向右都会感染
所以……应该可以了?
这题在算法数上看到过,不是很难,仔细想想就可以出来,但还是看了答案,哎,分清楚就好了
代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=51;
int n;
int main()
{
cin>>n;
int f,left=0,right=0;
cin>>f;
for(int i=1;i>x;
if(x>0&&abs(x)abs(f)) right++;
}
if((f<0&&left==0)||(f>0&&right==0)) cout<<1;
else cout<<(left+right+1);
return 0;
}
2、饮料换购
1216. 饮料换购 - AcWing题库
我的评价是签到题,不过竟然是蓝桥杯A组的题,开始有自信了
代码:
#include
#include
using namespace std;
int main()
{
int n;
cin>>n;
int ans=n,reminder=0;
while(n>=3)
{
ans+=n/3;
reminder=n%3;
n=n/3+reminder;
}
cout< 3、 01背包
啊这,基本功不扎实了
试一下先;
还行还记得点,但是还是寄了
很简单啊
dp[i] [j]表示选到第i个物品,最大的价值
那么状态转移方程也不难写
因为对于每件物品都有选和不选两种选择,分别对应两种情况,这时候取最大值就可以了;
dp[i] [j]= max(dp[i-1] [j], dp[i-1] [j-v[i]]+w[i]);(如果就j>=v[i])
dp[i] [j]= dp[i-1] [j] (如果j
代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int M=1010;
int N,V;
int v[M],w[M];
int dp[M][M];
int main()
{
cin>>N>>V;
for(int i=1;i<=N;i++)
cin>>v[i]>>w[i];
for(int i=1;i<=N;i++)
for(int j=0;j<=V;j++)
if(j < v[i])
dp[i][j] = dp[i - 1][j];
else dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
cout< 4、摘花生
简单的2维dp,不多说,上代码
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=101;
int g[N][N];
int dp[N][N];
int main()
{
int t;
cin>>t;
while(t--)
{
int c,r;
cin>>r>>c;
memset(dp,0,sizeof(dp));
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
cin>>g[i][j];
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+g[i][j];
cout< DAY9
1、错误票据
1204. 错误票据 - AcWing题库
额,只能说输入流没搞明白,
我反正觉得这题应该就是简单的,只要哈希一下就可以了
但是就是这个输入流用的很烂
读到文件末尾可以用(cin>>x).eof()来处理
下次记得了。
代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=1e6+10;
int a[N];
int l=N,r=0;
int main()
{
int n;
cin>>n;
int ans1,ans2;
int tmp;
while(!(cin>>tmp).eof())
{
a[tmp]++;
l=min(l,tmp);
r=max(r,tmp);
}
for(int i=l;i<=r;i++)
{
if(a[i]==0) ans1=i;
else if(a[i]==2) ans2=i;
}
cout< 我真的是傻瓜,为什么不while(cin>>tmp)呢?
2、剪格子
1206. 剪格子 - AcWing题库
这就是省赛的压轴题吗
恐怖如斯
我看看能不能做
首先我一开始想的是bfs,试一下:
发现不对
哎,看了答案就是dfs然后就剪枝,把和不是2倍的剪了,把s超过sum/2的剪了
打了遍代码,发现我的代码风格还是挺规范的(傲娇)
蓝桥杯好像和acwing的题不一样,不管了。
代码:
#include
#include
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
const int N=12;
int n,m;
int sum;
int ans=INF;
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
bool flag[N][N];
int g[N][N];
void dfs(int x,int y,int cnt,int s)
{
if(s==sum/2)
{
ans=min(ans,cnt);
return;
}
if(s>sum/2){
return;
}
for(int i=0;i<4;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx<=n&&nx>0&&ny<=m&&ny>0&&!flag[nx][ny])
{
flag[nx][ny]=1;
dfs(nx,ny,cnt+1,s+g[nx][ny]);
flag[nx][ny]=0;
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>g[i][j];
sum+=g[i][j];
}
if(sum%2==0)
{
flag[0][0]=1;
dfs(1,1,1,g[1][1]);
}
ans=(ans==INF?0:ans);
cout< DAY10
昨天颓了
*1、大臣的旅费(树形dp)
1207. 大臣的旅费 - AcWing题库
算每个城市之间的最大距离就类似那个数据结构里学的,数据量1e5感觉可以解决,试一下。
我的评价是直接寄,这个题遇到了一个没有见过的知识点:树的直径;
在每条边都有权值的情况下,树上两个最远点的距离就是树的直径
[投稿]2019年8月15日树的直径讲义 - AcWing
求法就是用树形dp,看上去也比较厉害
有点无语,真的好难
#include
#include
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll head[N*2],edge[N*2],nxt[N*2],ver[N*2];
ll dis[N],vis[N];
ll total=0,ans=0;
ll n,p,q,d;
void add(int u,int v,int w)
{
ver[++total]=v;
edge[total]=w;
nxt[total]=head[u];
head[u]=total;
}
void dp(int s)
{
vis[s]=1;
for(int i=head[s];i;i=nxt[i])
{
int y=ver[i];
if(vis[y]) continue;
dp(y);
ans=max(ans,dis[s]+dis[y]+edge[i]);
dis[s]=max(dis[s],dis[y]+edge[i]);
}
}
int main()
{
cin>>n;
for(int i=1;i>p>>q>>d;
add(p,q,d);
add(q,p,d);
}
dp(1);
cout< 我觉得我的图论可能要重新学起。
因为这个有n-1个操作所以才会想到用树存,树的很好用的存储方式就是
tot代表点的数量(最后一个点的标号)
用四个数组来存,ver是存儿子节点的编号的,edge是存边的权重的,next是存这个点的下一个兄弟节点,head是存这个节点的第一个儿子节点
树形dp就是求树的直径,也就是两个最远距离的点,那么最远距离的两个点就是对于公共祖宗节点,这个祖宗节点的最长链和次长链。用dp遍历一遍树,dp存最大的链,如果ans比dp[x]+dp[y]+edge[i]小就说明dp[x] 注意这个因为ans还要计算,所以拿long long存 痛苦 895. 最长上升子序列 - AcWing题库 字符串dp,先试一下 袁野:菜,我说不出话了,真的菜, 这个题应该是做过的啊,不知道为什么就是那么的脆弱,有一些可惜。 n^2的复杂度 代码: 1210. 连号区间数 - AcWing题库 题目描述半天实际就是枚举每个区间的最大值最小值,很简单 代码: 1212. 地宫取宝 - AcWing题库 感觉就是二维dp,试一下 抄了答案,我真没想到dp数组超二维,再加上两个坐标记录拿了多少物品和最大的价值 这样的话状态转移方程就可以写了,注意边界条件真的还是挺难的 还要注意边界检查,还有0价值的物品,反正挺离谱的 昨天又摆烂了 89. a^b - AcWing题库 这个题就是利用任何一个数都可以表示为2的幂之和,再利用a(2i)=(a(2(i-1)))^2得到 这样的话就可以用log^2b的复杂度得到结果 90. 64位整数乘法 - AcWing题库 这个题也是一样的,就是也是利用b可以表示成2的幂次的和,然后a*2^i=2a *2^(i-1) 代码: 这两题都是《算法竞赛进阶指南》的例题,详细的解析可以看到数上,其实我大概也明白了 1214. 波动数列 - AcWing题库 看上去直到是dp因为是组合问题,但是实在是想不明白到底是怎么样去dp [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oKfuG2zK-1644049163725)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220130104129476.png)] [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cumRDDUs-1644049163725)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220130104136855.png)] 思路大致如上,抄的代码,主要是组合问题一般是2维dp但是j具体选择什么量是需要好好思考的 学一波,打代码: 1215. 小朋友排队 - AcWing题库 一开始想用一些比较……暴力的方法来做的(因为看不出来应该用什么算法)但是很明显就是最小换位次数应该是左边有多少个比他大的数和右边有多少个比他小的数,那么就是求逆序数了。 看了看答案,确实不太可能会,因为别人用的就是树状数组,可以很快的求出逆序数,算出逆序数后就可以用 树状数组和线段树有些像(线段树是啥我也不太知道),它的原理又和前缀和比较像,也就是我的a[i]是我要存的数组,然后把它编程线段树以后 例如c[2]就包括a[1]+a[2]; 这是基本概念 然后就出现了几个比较离谱的操作: 1、位运算: 2、单点更新: 3、区间查询: 因为就是假设要得到sum(5); c[4]=a[1]+ a[2] +a[3] +a[4]; c[5]=a[5]; 所以就是将每个2进制上为1的位的树状数组项进行叠加; 树状数组可以很快的算出逆序对个数,也就是数组下标作为这个数,而数组记录每个数的个数,这样就可以算出逆序对的个数,也就是这题的思路 代码如下: 1217. 垒骰子 - AcWing题库 这个题看上去是dp,每个骰子从上往下看应该是有24种状态的,那么也是一种排列组合问题,先试一下 额,不是dp,这个题考的是快速矩阵乘法, 思路大概是每个色子从上往下看的那个面,每个面对应着4种方法,然后f[6]数组记录着最后一个骰子第i面的所有方法,第a[6] [6]记录着往上叠一个骰子的总共的方法,然后用矩阵的快速幂(刚学过)算矩阵的N次方,最后再乘f向量即可。 代码: 数组越界真的服了 1220. 生命之树 - AcWing题库 这个题我学会树形dp有思路了 试一下。 啊这,其实思路已经很对了,但是树形dp的编程过程仍然需要熟悉熟悉; 下次应该救会了,这个题世纪就是看子节点的dp结果和0相比的大小,因为最后只能选择最大的dp结果为答案, 其实就是连通域上的点的最大和。 代码: 1222. 密码脱落 - AcWing题库 这个题用dp,很像王丽萍讲过的最长子串匹配 其实如果有思路的话就是找出字符串和他的逆序字符串的最长子串 然后用总长度减去就好 但是想不到啊………… 代码: 大年初一开始学北大的算法课,现在开始做做北大算法课的作业 OpenJudge - 001:特殊密码锁 啊……枚举题都不会做,我真的服了,这个题因为假设要递归,那么他的2^30肯定超时了,所以只能枚举,并且枚举 代码: 其实和费解的开关一样,因为只要我枚举2种开头开关的情况,如果第i个开关和目标不一样,那么就改变第i+1个开关,直到第n-1个开关,这时候查看第n个开关的状态判断是否满足条件,这个时候不会超时 2进制的巧用和清晰的思路是解决这类题的关键 OpenJudge - 002:拨钟问题 这个题也是让我大受震撼,首先,有九种枚举的方式,假设把这九种方式都枚举出来,那么算出来应该是9重循环,然后最后是49次的结果也就是218次方,肯定没超时,绝对是可以做的吧 暴力枚举肯定可以做的 然后我去找答案发现确实又很厉害的方式 网上的答案代码,算的更快: OpenJudge - 003:全排列 感觉比较轻松,这种题现在也比较熟练了 代码 很常见的递归题,我用了栈,其实可以不用栈的,但是其实都一样,就是每次得到的数如果比2大那就在递归的打印出来直到比2小结束递归就可以了 我的代码: 别人的代码思路就是减掉2进制最大位数的1,也很厉害很清楚 OpenJudge - 005:Boolean Expressions 服了,这一个递归题竟然在IO上弄了半天 哎getline(cin,string)我真的是用一次忘一次 问题的思路很简单,就是分成两种,一种是表达式,表达式通过|和&连接,需要事先用项去算,另一种是项,项又分三种,一种是()里包含着表达式,通过表达式的值去算,第二种就是通过!直接获得取反的值,第三种就是直接获得该值。 思路不难,代码如下: OpenJudge - 006:简单的整数划分问题 这题决定用dp做锻炼一下 我真的无语,这个题简直就是最简单的dp稍微推出来做一下就可以了 我是直接暴力拿数学推出的dp公式,代码如下 OpenJudge - 012:拦截导弹 这题简单1维线性dp怎么都会做 状态转移方程就是:dp[i]=max{ dp [j] + 1 }(其中0<=j
要注意的是dp[i]其实为1 代码: OpenJudge - 013:Zipper 思路来源于网上(其实也不是想不到,真的就是想复杂了):(64条消息) Zipper动态规划_hejnhong的博客-CSDN博客 String 3能由前两个字符串中的字符混合而成,显然,它的子字符串也必然能由前两个字符串混合成。反之,如果String 3的子串不能由String 1和String 2混合而成,那么该问题的答案就是 no。基于此,我们首先从String 3的第一个字符开始判断,依次到前两个,前三个……如果直到最后的全部字符都满足条件则答案是yes。 定义String 3的前 i+j 个字符,能否由String 1的前 i 个字符和String 2 的前 j 个字符组成的问题,为Yes[i][j]。(注意,这里的 i、j 不是下标,本题的下标都从0开始。)共有两种情况: (1)String 1 的第 i 个字符是String 3 的第 i+j 个字符,也即String 1[i-1]=String 3[i+j-1],此时子问题为String 3 的前 i+j-1个字符能否由String 1的前 i-1 个字符和String 2的前 j 个字符组成,即 Yes[i-1][j];DAY11
1、最长上升子序列
#include2、连号区间数
#include*3、地宫取宝
#includeDAY12
1、快速幂
#include2、64位快速乘法
#include3、波动数列
#includeDAY13
*1、小朋友排队
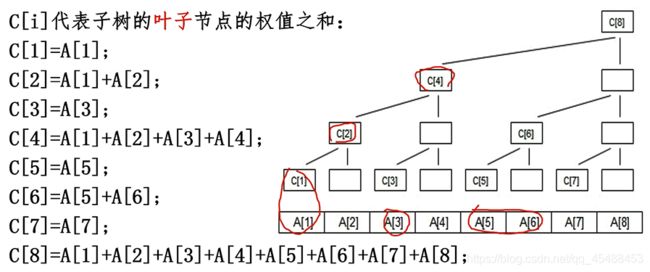
int lowbit(x){return x&(-x);}返回最低位的1代表的数值,
void update(int x,int y,int n){
for(int i=x;i<=n;i+=lowbit(i)) //x为更新的位置,y为更新后的数,n为数组最大值
c[i] += y;
}
int getsum(int x){
int ans = 0;
for(int i=x;i;i-=lowbit(i))
ans += c[i];
return ans;
}
#include2、垒骰子
#includeDAY14
1、生命之树
#include2、密码脱落
#includeDAY15(枚举)
1、特殊密码锁
#include2、拨钟问题
//拨钟问题
#include"stdafx.h"
#includeDAY16(递归)
1、全排列问题
#include2、2的幂次方表示
#include#includeDay17(递归)
1、表达式问题
#include2、简单数的划分
#includeDAY18(动态规划1)
1、拦截导弹
#include2、Zipper
(2)String 2 的第 j 个字符是String 3 的第 i+j 个字符,也即String 2[j-1]=String 3[i+j-1],此时子问题为String 3 的前 i+j-1个字符能否由String 1的前 i 个字符和String 2的前 j-1 个字符组成,即 Yes[i][j-1]。
代码: #include