Machine Learning with Python Cookbook 学习笔记 第11章
Chapter 11. Model Evaluation
前言
- 本笔记是针对人工智能典型算法的课程中Machine Learning with Python Cookbook的学习笔记
- 学习的实战代码都放在代码压缩包中
- 实战代码的运行环境是python3.9 numpy 1.23.1 **anaconda 4.12.0 **
- 上一章:(97条消息) Machine Learning with Python Cookbook 学习笔记 第10章_五舍橘橘的博客-CSDN博客
- 代码仓库
- Github:yy6768/Machine-Learning-with-Python-Cookbook-notebook: 人工智能典型算法笔记 (github.com)
- Gitee:yyorange/机器学习笔记代码仓库 (gitee.com)
11.0 Introduction
- 在本章中,我们将研究如何评估我们学习算法所创建模型的质量。
- 从根本上说,机器学习不是创建模型,而是创建有高质量的模型
- 所以如何评估一个模型的好坏就显得尤为重要
11.1 Cross-Validating Models
- 交叉验证模型
- 创建一个管道来预处理数据、训练模型,然后使用交叉验证对其进行评估:
CV.py
# Load libraries
from sklearn import datasets
from sklearn import metrics
from sklearn.model_selection import KFold, cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
# 加载手写数字数据集
digits = datasets.load_digits()
# 特征矩阵
features = digits.data
# 目标向量
target = digits.target
# 标准化
standardizer = StandardScaler()
# 逻辑回归
logit = LogisticRegression()
# 复合估计器
pipeline = make_pipeline(standardizer, logit)
# 创建KFold cv
kf = KFold(n_splits=10, shuffle=True, random_state=1)
# 执行 k-fold cross-validation
cv_results = cross_val_score(pipeline, # Pipeline
features, # Feature matrix
target, # Target vector
cv=kf, # Cross-validation technique
scoring="accuracy", # Loss function
n_jobs=-1) # Use all CPU scores
# 计算平均值
print(cv_results.mean())
![]()
Discussion
-
我们的目标不是评估模型在我们的训练数据上的表现如何,而是它在从未见过的数据(例如,新客户、新犯罪、新图像)上的表现如何。出于这个原因,我们的评估方法应该帮助我们了解模型能够如何从他们从未见过的数据中做出预测。
-
一种策略可能是推迟一部分数据进行测试。这称为验证(或保留)。
- 在验证中,我们的观察(特征和目标)分为两组,传统上称为训练集和测试集。我们把测试集放在一边,假装我们以前从未见过它。
- 我们使用我们的训练集训练我们的模型,使用特征和目标向量来教模型如何做出最佳预测。
- 我们通过评估我们在训练集上训练的模型在测试集上的表现来模拟从未见过的外部数据。
- 验证法的缺点:
- 模型的性能可能高度依赖于为测试集选择的少数观测值。
- 模型没有使用所有可用数据进行训练,也没有根据所有可用数据进行评估。
-
更好的策略:KFCV —— k重交叉验证
-
在 KFCV 中,我们将数据分成 k 个部分,称为“折叠”。 然后使用 k – 1 折对模型进行训练——合并为一个训练集——然后将最后一个折用作测试集.
-
我们重复这 k 次,每次使用不同的折叠作为测试集。 然后对每个 k 次迭代的模型性能进行平均以产生整体测量。
-
在案例中,我们使用了10折进行KFCV,并将结果输出到cv_results
# 查看结果 print(cv_results) -
KFCV的三个要点:
-
IID:首先,KFCV 假设每个观察都是独立于另一个创建的(即数据是独立同分布). 如果数据是独立同分布的,那么在分配给折叠时打乱观察是个好主意。 在
scikit-learn中,我们可以设置shuffle=True来执行洗牌。 -
通常在k个folder中,每个类所占的百分比基本相同。在
scikit-learn中,我们可以通过将KFold类替换为StratifiedKFold来进行分层 k 折交叉验证。 -
当我们使用验证集或交叉验证时,重要的是基于训练集预处理数据,然后将这些转换应用于训练集和测试集。如,当我们进行标准化时,我们只计算训练集的均值和方差(fit)。 然后我们将该
StandardScaler(transform)到应用于训练集和测试集:# Import library from sklearn.model_selection import train_test_split # 创建测试集和训练集 features_train, features_test, target_train, target_test = train_test_split( features, target, test_size=0.1, random_state=1) # Fit 训练集,不运用到测试集 standardizer.fit(features_train) # transform 训练集和测试集 features_train_std = standardizer.transform(features_train) features_test_std = standardizer.transform(features_test)这样做的原因是因为我们假装测试集是未知数据。如果我们使用来自训练集和测试集的观察来拟合我们的预处理器,则来自测试集的一些信息会泄漏到我们的训练集中。此规则适用于任何预处理步骤,例如特征选择。
-
-
scikit-learn’s
pipelinepackage:-
pipeline包很容易做到上述第三点,首先我们创建一个pipeline; -
然后我们使用该管道运行 KFCV,scikit 为我们完成所有工作;
# 创建 pipeline pipeline = make_pipeline(standardizer, logit) # Do k-fold cross-validation scikit 为我们完成所有工作 cv_results = cross_val_score(pipeline, # 管道 features, # 特征矩阵 target, # 目标向量 cv=kf, # CV 采用的方法,这里是KFolder scoring="accuracy", # 损失函数,这里是准确度 n_jobs=-1) # 使用所有CPU来评估,如果是正数并行的数量 -
cross_val_score 带有三个值得注意的参数
-
cv 决定了我们的交叉验证技术。常用的有:KFold、LeaveOneOut
- scoring损失函数:常见的有分类型:‘precision’ (准确率)和 ’recall‘ (召回率)和 ’f1‘(前两者的调和平均数),聚类型:adjusted_mutual_info_score、回归型:neg_mean_squared_error
文档:3.3. Metrics and scoring: quantifying the quality of predictions — scikit-learn 1.1.1 documentation
- 并行评估的数量,-1表示用所有处理器
-
-
-
11.2 Creating a Baseline Regression Model
- 使用一个baseline(理解为朴素的、启发式的)的线性回归模型和自己的模型结果作比对
DummyRegressor
dummyRegressorExample.py
# Load libraries
from sklearn.datasets import load_boston
from sklearn.dummy import DummyRegressor
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing
# 波士顿房价数据集被移除,换成fetch_california_housing
housing = fetch_california_housing()
# 特征矩阵、目标
features, target = housing.data, housing.target
# 分离测试集和训练集
features_train, features_test, target_train, target_test = train_test_split(
features, target, random_state=0)
# 创建一个DummyRegressor
dummy = DummyRegressor(strategy='mean')
# 训练它
dummy.fit(features_train, target_train)
# 得到R^2得分
print(dummy.score(features_test, target_test))
# Load library
from sklearn.linear_model import LinearRegression
# 训练一个简单的线性模型
ols = LinearRegression()
ols.fit(features_train, target_train)
# 得分
print(ols.score(features_test, target_test))
Discussion
- DummyRegressor 允许我们创建一个非常简单的模型,我们可以将其用作基线来与我们的实际模型进行比较。
- DummyRegressor 使用 strategy 参数设置进行预测的方法,包括训练集中的均值或中值。 此外,如果我们将策略设置为常量并使用常量参数,我们可以设置虚拟回归器来预测每个观察值的某个常量值:
# 每一次都预测为20
clf = DummyRegressor(strategy='constant', constant=20)
clf.fit(features_train, target_train)
# 得分
print(clf.score(features_test, target_test))
![]()
-
R 2 R^2 R2评分:
R 2 = 1 − Σ i ( y i − y i ^ ) Σ i ( y i − y ‾ ) R^2 = 1- \frac{\Sigma_i(y_i-\hat{y_i})}{\Sigma_i(y_i-\overline{y})} R2=1−Σi(yi−y)Σi(yi−yi^)
y i ^ \hat{y_i} yi^是预测值, y ‾ \overline{y} y是目标均值
R 2 R^2 R2越接近1,目标向量中由特征解释的方差越大,拟合越好。
11.3 Creating a Baseline Classification Model
- 创建一个baseline的分类器
DummyClassifier
dummyClassifier.py
# Load libraries
from sklearn.datasets import load_iris
from sklearn.dummy import DummyClassifier
from sklearn.model_selection import train_test_split
# 莺尾花数据
iris = load_iris()
# 创建target vector feature matrix
features, target = iris.data, iris.target
# 分离训练集和测试集
features_train, features_test, target_train, target_test = train_test_split(
features, target, random_state=0)
# 创建 dummy classifier
dummy = DummyClassifier(strategy='uniform', random_state=1)
# "训练" model
dummy.fit(features_train, target_train)
# 获得准确性的评分
print(dummy.score(features_test, target_test))
# Load library
from sklearn.ensemble import RandomForestClassifier
# 创建一个随机森林的分类器(14章会介绍原理)
classifier = RandomForestClassifier()
# 训练模型
classifier.fit(features_train, target_train)
# 得到准确性的评分
print(classifier.score(features_test, target_test))
Discussion
- 分类器的一个常见的评判标准就是它比随机预测好多少。
DummyClassifier就是进行随机猜测。- 一个重要的参数是
strategy:- stratified:返回类的概率就是训练集中类的频率;
- uniform:从 y 中观察到的唯一类列表中随机均匀地生成预测,即每个类具有相等的概率。
- prior:默认值。predict总是返回最频繁出现的类
- 其他取值:sklearn.dummy.DummyClassifier — scikit-learn 1.1.1 documentation
11.4 Evaluating Binary Classifier Predictions
- 给定一个已经训练好的二分类模型,评价它的质量
Solution:二分类器评价原理
- 使用 scikit-learn 的 cross_val_score 进行交叉验证,同时使用打分参数定义多个性能指标之一,包括准确度、精确度、召回率和 F1。
- 准确性是一种常见的性能指标。 它只是正确预测的观察值的比例:
- A c c u r a n c y = T P + T N T P + T N + F P + F N Accurancy = \frac{TP+TN}{TP+TN+FP+FN} Accurancy=TP+TN+FP+FNTP+TN
- TP:真阳性数量
- TN:真阴性数量
- FP:假阳性数量
- FN:假阴性数量
- 参数
scoring="accuracy" - 缺点:在存在高度不平衡的类模型中,准确性的评估能力较差。例如假设我们试图预测一种非常罕见的癌症,这种癌症发生在 0.1% 的人群中。在训练我们的模型后,我们发现准确率为 95%。然而,99.9% 的人没有患上癌症:如果我们简单地创建一个模型来“预测”没有人患上这种癌症,那么我们的幼稚模型的准确率会提高 4.9%,但显然无法预测任何事情。
evaluateClassifier.py
# Load libraries
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# 生成 features matrix and target vector
X, y = make_classification(n_samples=10000,
n_features=3,
n_informative=3,
n_redundant=0,
n_classes=2,
random_state=1)
# 创建 logistic regression
logit = LogisticRegression()
# CV打分函数,scoring为accuracy
# 与原书不同,现在cv函数打分的默认k值改成了5,所以数组有5个元素
print(cross_val_score(logit, X, y, scoring="accuracy"))
![]()
-
precision:实际预测正确的阳性观察结果在预测正确中的比例。
-
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
-
high-precision模型是悲观的,因为它们只有在非常确定的时候才认为观测结果是阳性
# CV 打分函数 scoring为 precision print(cross_val_score(logit, X, y, scoring="precision"))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N8g91Qwc-1658503259994)(C:\Users\12587\AppData\Roaming\Typora\typora-user-images\image-20220721231443766.png)]
-
-
recall:预测为阳性的结果在真正为阳性的比率。
-
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
-
衡量模型识别正类观察的能力。
-
high-recall的模型是乐观的,因为他们把一个类判断成阳性的标准较低
# CV 打分函数 scoring为 recall print(cross_val_score(logit, X, y, scoring="recall"))
-
-
我们希望precision和recall间能有某种平衡:
F1-
F1 分数是调和平均值
-
F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F_1=2\times \frac{Precision\times Recall}{Precision+Recall} F1=2×Precision+RecallPrecision×Recall
-
# CV 打分函数 scoring为 f1 print(cross_val_score(logit, X, y, scoring="f1"))
-
![]()
Discussion
-
作为一种评估指标,准确率具有一些有价值的特性,尤其是其简单的直觉。
-
更好的指标通常涉及使用精确度和召回率的某种平衡——即我们模型的乐观和悲观之间的权衡。 F1 代表召回率和准确率之间的平衡,其中两者的相对贡献相等。
-
作为使用 cross_val_score 的替代方法,如果我们已经有了真实的 y 值和预测的 y 值,我们可以直接计算准确度和召回等指标:
# Load library from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # 创建测试集和训练集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=1) # 对目标向量作出预测 y_hat = logit.fit(X_train, y_train).predict(X_test) # Calculate accuracy print(accuracy_score(y_test, y_hat))
11.5 Evaluating Binary Classifier Thresholds
- 需要评估分类器以及各种阈值
Solution:ROC曲线
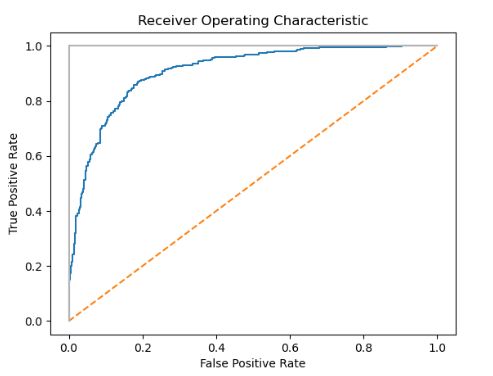
- Receiving Operating Characteristic (ROC) curve 是评估二元分类器质量常用的方法。
- ROC 比较每个概率阈值(即,将观察预测为一个类别的概率)处的真阳性和假阳性的存在。
- 绘制 ROC 曲线,我们可以看到模型的表现。 正确预测每个观察结果的分类器看起来像下图中的浅灰色实线,立即直上顶部。 随机预测的分类器将显示为对角线。
- 绘制 ROC 曲线,我们可以看到模型的表现。 正确预测每个观察结果的分类器看起来像下图中的浅灰色实线,立即直上顶部。 随机预测的分类器将显示为对角线。
- 在 scikit-learn 中,我们可以使用 roc_curve 计算每个阈值的真假阳性,然后绘制它们:
rob_curveExample.py
# Load libraries
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
# 创建特征矩阵和目标向量
features, target = make_classification(n_samples=10000, # 10000个样本
n_features=10, # 10个特征
n_classes=2, # 2个类别
n_informative=3, # 参与建模的特征数为3个
random_state=3) # 随机种子
# 分离训练集和测试集
features_train, features_test, target_train, target_test = train_test_split(
features, target, test_size=0.1, random_state=1)
# 创建LogisticRegression 分类器
logit = LogisticRegression()
# 训练模型
logit.fit(features_train, target_train)
# 预测结果
target_probabilities = logit.predict_proba(features_test)[:, 1]
# 错误和正确的比例
false_positive_rate, true_positive_rate, threshold = roc_curve(target_test,
target_probabilities)
# 使用pyplot绘制ROC曲线图
plt.title("Receiver Operating Characteristic")
plt.plot(false_positive_rate, true_positive_rate)
plt.plot([0, 1], ls="--")
plt.plot([0, 0], [1, 0], c=".7"), plt.plot([1, 1], c=".7")
plt.ylabel("True Positive Rate")
plt.xlabel("False Positive Rate")
plt.show()
Discussion
- 到目前为止,我们只检查了基于它们预测的值的模型。 然而,在许多学习算法中,这些预测值是基于概率估计的。 也就是说,每个观察都被赋予了属于每个类别的明确概率。
- 我们可以使用
predict_proba查看第一次观察的预测概率:
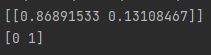
# 获取第一个observation的分类概率
print(logit.predict_proba(features_test)[0:1])
-
预测的类别
classes_# 预测的结果 print(logit.classes_) -
第一次观察有大约 87% 的机会属于阴性类 (0),有 13% 的机会属于阳性类 (1)。默认情况下,如果概率大于 0.5(称为阈值),scikit-learn 会预测观察结果是阳性类的一部分。
-
出于实质性原因,我们通常希望明确地偏向我们的模型以使用不同的阈值,而不是中间立场。例如,如果误报对我们公司来说代价高昂,我们可能更喜欢具有高概率阈值的模型。
-
当一个观察结果被预测为阳性时,我们可以非常确信预测是正确的。这种权衡以真阳性率 (TPR) 和假阳性率 (FPR) 表示。真阳性率是正确预测为真的观察值除以所有真阳性观察值:
-
T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP
-
F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP
-
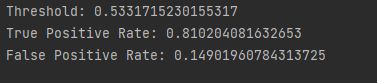
ROC 曲线代表每个概率阈值的相应 TPR 和 FPR。 例如,在我们的解决方案中,大约 0.50 的阈值具有 0.81 的 TPR 和 0.15 的 FPR
-
# 阈值大约为0.5 print("Threshold:", threshold[116]) print("True Positive Rate:", true_positive_rate[116]) print("False Positive Rate:", false_positive_rate[116]) -
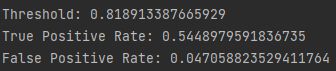
然而,如果我们将阈值提高到约 80%(即,提高模型在预测观察结果为正之前必须具有的确定性),TPR 会显着下降,但 FPR 也会下降:
# 阈值提升到0.8 print("Threshold:", threshold[45]) print("True Positive Rate:", true_positive_rate[45]) print("False Positive Rate:", false_positive_rate[45])- 我们对被预测为阳性类的更高要求使得模型无法识别多个阳性样本(较低的 TPR),但也减少了来自被预测为阳性,实际为阴性样本的噪声(较低的 FPR)。
-
-
除了能够可视化 TPR 和 FPR 之间的权衡之外,ROC 曲线还可以用作模型的通用度量。 模型越好,曲线就越高,因此曲线下的面积就越大。
-
通常通过计算 ROC 曲线下面积 (AUCROC) 来判断模型在所有可能阈值下的整体相等性。 AUCROC 越接近 1,模型越好。 在 scikit-learn 中,我们可以使用 roc_auc_score 计算 AUCROC:
# 计算曲线面积 print(roc_auc_score(target_test, target_probabilities))
11.6 Evaluating Multiclass Classifier Predictions
- 评估多类分类器模型的质量
cross-validation
evaluateMultiClassifier.py
# Load libraries
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# 特征矩阵,目标向量
features, target = make_classification(n_samples=10000,
n_features=3,
n_informative=3,
n_redundant=0,
n_classes=3,
random_state=1)
# 创建 logistic regression
logit = LogisticRegression()
# 使用accuracy指标进行判断
# 与原书不同,现在cv函数打分的默认k值改成了5,所以数组有5个元素
print(cross_val_score(logit, features, target, scoring='accuracy'))
Discussion
-
当我们有分布平衡的类时(例如,目标向量的每个类中的观察数量大致相等),就像在二元类设置中一样,准确度是评估指标的一个简单且可解释的选择。准确性是正确预测的数量除以观察的数量,并且在多类和二元设置中的效果一样好。然而,当我们有不平衡的类(一种常见情况)时,我们应该倾向于使用其他评估指标。
-
许多 scikit-learn 的内置指标用于评估二元分类器。
-
但是,当我们有两个以上的类时,可以扩展这些指标中的许多指标以供使用。精度、召回率和 F1 分数是我们在之前的秘籍中已经详细介绍过的有用指标。虽然它们最初都是为二元分类器设计的,但我们可以通过将我们的数据视为一组二元类来将它们应用于多类设置。
# Cross-validate模型 使用 macro averaged F1 score print(cross_val_score(logit, features, target, scoring='f1_macro'))
-
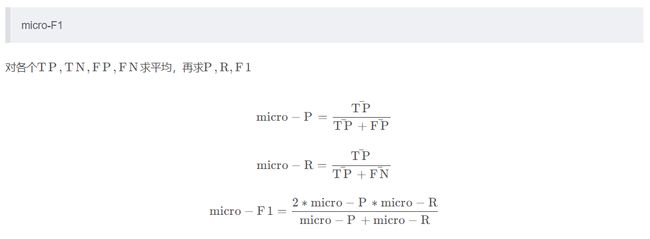
这里的scoring函数后面带着_macro其实是用于平均类评估参数的方法,下面是比较常见的多类评估后缀:
-
macro:
计算每个类的度量分数的平均值,对每个类进行平均加权。(平均值)
-
weighted:
计算每个类的度量分数的平均值,根据数据中的大小对每个类进行加权。
-
micro
计算每个类的度量分数的平均值,根据数据中的大小对每个类进行加权。
-
-
通俗的来说其实是:
-
参考资料:(97条消息) 多分类算法的评估指标_taon1607的博客-CSDN博客_多分类算法评价标准
11.7 Visualizing a Classifier’s Performance
- 分类结果可视化
- 绘制混淆矩阵(confusion matrix)
confusionMatrix.py
seaborn库需要安装
- seaborn库介绍:功能强大的python包(三):Seaborn - 知乎 (zhihu.com)
- seaborn其实就是一个基于matplotlib和pandas的绘制库
conda install seaborn
# Load libraries
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import pandas as pd
# 莺尾花数据集
iris = datasets.load_iris()
# 特征矩阵
features = iris.data
# 特征向量
target = iris.target
# 创建一个数组包含所有类别的名字
class_names = iris.target_names
# 创建训练集和测试集
features_train, features_test, target_train, target_test = train_test_split(
features, target, random_state=1)
# sigmoid函数回归
classifier = LogisticRegression()
# 训练并且预测
target_predicted = classifier.fit(features_train,
target_train).predict(features_test)
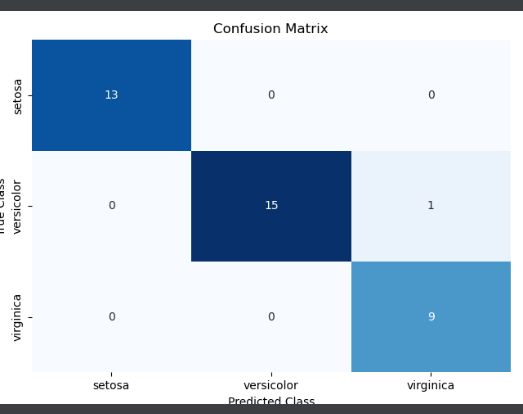
# confusion_matrix创建混淆矩阵
matrix = confusion_matrix(target_test, target_predicted)
# 创建 pandas dataframe(绘制需要是pandas的格式)
dataframe = pd.DataFrame(matrix, index=class_names, columns=class_names)
# 创建heatmap
sns.heatmap(dataframe, annot=True, cbar=None, cmap="Blues")
plt.title("Confusion Matrix"), plt.tight_layout()
plt.ylabel("True Class"), plt.xlabel("Predicted Class")
plt.show()
Discussion
-
混淆矩阵是分类器性能的简单、有效的可视化。
-
矩阵的每一列(通常可视化为heatmap)
- heatmap是常见的一种可视化运用到机器学习中,seaborn也有相关的库函数创建和编辑它
- 数字越大颜色越深
- 关于heatmap - 简书 (jianshu.com)
-
关于混淆矩阵,有三件事值得注意。
- 一个完美的模型将沿对角线具有值,并且在其他任何地方都具有零。一个糟糕的模型统计的样本数量都集中在边缘的单元格中。
- 混淆矩阵让我们不仅可以看到模型哪里出错了,还可以看到它是如何出错的(不在对角线上的元素)
- 混淆矩阵适用于任意数量的类(尽管如果我们的目标向量中有 100 万个类,混淆矩阵的可视化可能难以阅读)。
-
关于sklearn.metrics中的混淆矩阵相关的函数:sklearn.metrics.confusion_matrix — scikit-learn 1.1.1 documentation
11.8 Evaluating Regression Models
- 评估回归模型
mean squared error (MSE),中文翻译应该是均方误差
MSE.py
# Load libraries
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
# 生成 features matrix, target vector
features, target = make_regression(n_samples=100,
n_features=3,
n_informative=3,
n_targets=1,
noise=50,
coef=False,
random_state=1)
# 创建线性回归模型
ols = LinearRegression()
# 交叉检验法 linear regression 使用 (negative) MSE
print(cross_val_score(ols, features, target, scoring='neg_mean_squared_error'))
# 交叉检验法 linear regression 使用 R方
print(cross_val_score(ols, features, target, scoring='r2'))
Discussion
- MSE 是回归模型最常用的评价指标之一。
- M S E = 1 n Σ i = 1 2 ( y ^ i − y i ) 2 MSE = \frac{1}{n}\Sigma_{i=1}^2(\hat y_i-y_i)^2 MSE=n1Σi=12(y^i−yi)2
- 其中 n 是观察次数,yi 是我们试图预测的目标的真实值,用于观察 i,并且是模型对 yi 的预测值。
- MSE 是预测值和真实值之间所有距离的平方和的度量。 MSE 的值越高,总平方误差越大,因此模型越差。
- 默认情况下,在 scikit-learn 中,评分参数的参数假定较高的值优于较低的值。 但是,对于 MSE,情况并非如此,更高的值意味着更差的模型。 出于这个原因,scikit-learn 使用 neg_mean_squared_error 参数查看负 MSE。
- 一个常见的替代回归评估指标是 R2 ,它测量模型解释的目标向量中的方差量。(参考11.2节)
- R 2 = 1 − Σ i ( y i − y i ^ ) Σ i ( y i − y ‾ ) R^2 = 1- \frac{\Sigma_i(y_i-\hat{y_i})}{\Sigma_i(y_i-\overline{y})} R2=1−Σi(yi−y)Σi(yi−yi^)
11.9 Evaluating Clustering Models
- 评估一个无监督聚类模型的质量
silhouette coefficients(轮廓系数)
silhouetteCoeff.py
import numpy as np
from sklearn.metrics import silhouette_score
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# Generate 特征矩阵
features, _ = make_blobs(n_samples=1000,
n_features=10,
centers=2,
cluster_std=0.5, # 聚类的标准差
shuffle=True,
random_state=1)
# 使用 k-means 去预测分类(第19章介绍)
model = KMeans(n_clusters=2, random_state=1).fit(features)
# 获得分完类预测所得到的标签
target_predicted = model.labels_
# 使用silhouette coefficients 预测
print(silhouette_score(features, target_predicted))
Discussion
- 聚类预测是无监督模型,特点在于没有目标向量,如果没有目标向量,我们无法评估预测值与真实值
- 但我们可以评估集群本身的性质。
- 我们可以想象“好”集群在同一集群中的观测值之间的距离非常小(即密集集群),而不同集群之间的距离很大(即分离良好的集群)。
silhouette coefficients是一个同时衡量这两个属性的单一值- s i = b i − a i m a x ( a i , b i ) s_i= \frac{b_i-a_i}{max(a_i,b_i)} si=max(ai,bi)bi−ai其中 si 是观测 i 的轮廓系数,ai 是 i 与同一类的所有观测之间的平均距离,bi 是 i 与来自不同类的最近聚类的所有观测之间的平均距离。
silhouette_score返回的值是所有observation的平均轮廓系数。轮廓系数介于 –1 和 1 之间,其中 1 表示密集、分离良好的集群。- api:sklearn.metrics.silhouette_score — scikit-learn 1.1.1 documentation
11.10 Creating a Custom Evaluation Metric
- 创建自定义的度量方法
make_scorer
make_scorer.py
# Load libraries
from sklearn.metrics import make_scorer, r2_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.datasets import make_regression
# 生成特征矩阵和目标向量
features, target = make_regression(n_samples=100,
n_features=3,
random_state=1)
# 生成测试集和训练集
features_train, features_test, target_train, target_test = train_test_split(
features, target, test_size=0.10, random_state=1)
# 创建一个自定义的评估度量函数
def custom_metric(target_test, target_predicted):
# 计算r2_score
r2 = r2_score(target_test, target_predicted)
# 返回
return r2
# 定义scorer,然后greater_is_better表明分数越高模型越好
score = make_scorer(custom_metric, greater_is_better=True)
# 脊回归
classifier = Ridge()
# 训练脊回归模型
model = classifier.fit(features_train, target_train)
# 使用自定义的scorer
print(score(model, features_test, target_test))
![]()
Discussion
-
make_scorer需要我们定义一个函数f:
- f接受两个参数:ground_truth(目标向量)、predicted(我们的预测值)
-
make_scorer需要
greater_is_better指定是否是分越高越好 -
在案例中我们将R2假装成我们自定义的判断方法来作为
# 预测值 target_predicted = model.predict(features_test) # 使用r2_score评分 print(r2_score(target_test, target_predicted)) -
关于示例出现的Ridge回归:(中文翻译用岭回归也有翻译成脊回归的)
- Ridge是线性回归的一种改良,在线性回归的基础上增加一个正则项(惩罚项)
- 当X不是列满秩时,或者某些列之间的线性相关性比较大时,
X T X X^TX XTX的行列式接近于0,不能采用最小二乘法进行求解。 - 所以我们添加一个正则项, Γ θ \Gamma\theta Γθ
- 讲的比较详细的资料:简单易学的机器学习算法——岭回归(Ridge Regression) - 腾讯云开发者社区-腾讯云 (tencent.com)
11.11 Visualizing the Effect of Training Set Size
-
评估Observation的数量对模型质量的影响
-
绘制
learning curve
learningCurve.py
# Load libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
# 手写数字集
digits = load_digits()
# 特征矩阵和目标向量
features, target = digits.data, digits.target
# 创建多种数据集大小对应的cv检验的结果
train_sizes, train_scores, test_scores = learning_curve(
# 分类器——随机森林
RandomForestClassifier(),
# 特征矩阵
features,
# 目标向量
target,
# Kfolds
cv=10,
# 评估函数
scoring='accuracy',
# 所有CPU参与评估
n_jobs=-1,
# 大小为50
# 训练集
train_sizes=np.linspace(
0.01, #百分之1
1.0, #百分百
50))
# 训练集平均值和标准差
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
# 测试集的平均值和标准差
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
# 绘制
plt.plot(train_sizes, train_mean, '--', color="#111111", label="Training score")
plt.plot(train_sizes, test_mean, color="#111111", label="Cross-validation score")
# 绘制条带
plt.fill_between(train_sizes, train_mean - train_std,
train_mean + train_std, color="#DDDDDD")
plt.fill_between(train_sizes, test_mean - test_std,
test_mean + test_std, color="#DDDDDD")
# 坐标系
plt.title("Learning Curve")
plt.xlabel("Training Set Size"), plt.ylabel("Accuracy Score"),
plt.legend(loc="best")
plt.tight_layout()
plt.show()
Discussion
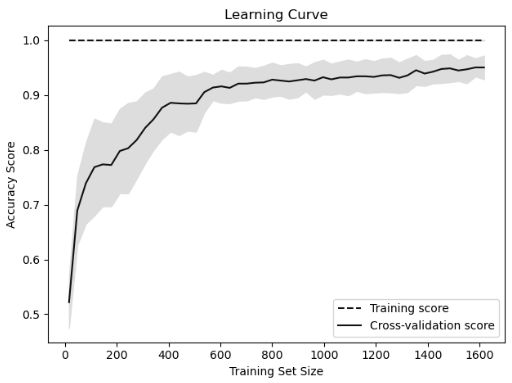
- 随着训练集中观察数量的增加,学习曲线可视化模型在训练集和交叉验证期间的性能(例如,准确性、召回率)。 它们通常用于确定我们的学习算法是否会从收集额外的训练数据中受益。
- 我们绘制了随机森林分类器在 50 个不同的训练集大小(从 1% 到 100% 的观测值)下的准确度。 交叉验证模型的准确性得分不断提高告诉我们,我们可能会从额外的观察中受益(尽管在实践中这可能不可行)。
11.12 Creating a Text Report of Evaluation Metrics
- 输出模型评估结果的基本信息
classification_report
textReportofEvaluation.py
# Load libraries
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# 加载莺尾花数据集
iris = datasets.load_iris()
# 特征矩阵
features = iris.data
# 目标向量
target = iris.target
# 类的名字
class_names = iris.target_names
# 训练集和测试集
features_train, features_test, target_train, target_test = train_test_split(
features, target, random_state=1)
# 创建 logistic regression
classifier = LogisticRegression()
# 训练模型并作出预测
model = classifier.fit(features_train, target_train)
target_predicted = model.predict(features_test)
# 创建分类器评估结果的简短描述
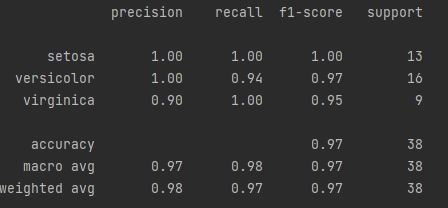
print(classification_report(target_test,
target_predicted,
target_names=class_names))
Discussion
- Classification_report 为我们提供了一种快速查看一些常见评估指标的方法
- precision
- recall
- F1-score
- support:每个类的observation的个数
11.13 Visualizing the Effect of Hyperparameter Values
-
评估不同超参数对模型的影响
-
绘制
validation curvevalidationCurve.py
# Load libraries import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_digits from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import validation_curve # 手写数字集 digits = load_digits() # 特征矩阵,目标矩阵 features, target = digits.data, digits.target # 生成一个数组从1到250,步长为2作为超参数数组 param_range = np.arange(1, 250, 2) # 通过不同的参数生成training and test train_scores, test_scores = validation_curve( # 随机森林的分类器 RandomForestClassifier(), # 特征矩阵 features, # 目标向量 target, # 超参数 param_name="n_estimators", # 超参数的范围 param_range=param_range, # KFold的k值 cv=3, # 评估标准 scoring="accuracy", # 使用所有CPU n_jobs=-1) # 计算训练集的平均值和标准差 train_mean = np.mean(train_scores, axis=1) train_std = np.std(train_scores, axis=1) # 计算测试集的平均值和标准差 test_mean = np.mean(test_scores, axis=1) test_std = np.std(test_scores, axis=1) # 绘制accuracy plt.plot(param_range, train_mean, label="Training score", color="black") plt.plot(param_range, test_mean, label="Cross-validation score", color="dimgrey") # 绘制accuracy的条带 plt.fill_between(param_range, train_mean - train_std, train_mean + train_std, color="gray") plt.fill_between(param_range, test_mean - test_std, test_mean + test_std, color="gainsboro") # 绘制 plt.title("Validation Curve With Random Forest") plt.xlabel("Number Of Trees") plt.ylabel("Accuracy Score") plt.tight_layout() plt.legend(loc="best") plt.show()
Discussion
- 大多数训练算法都必须在训练前选择自己的超参数
- 本案例中我们使用的随机森林算法(第14章会介绍),其中的一个超参数就是森林中决策树的数量
- 大多数超参数是在模型选择(Model Selection)的阶段进行被选择的
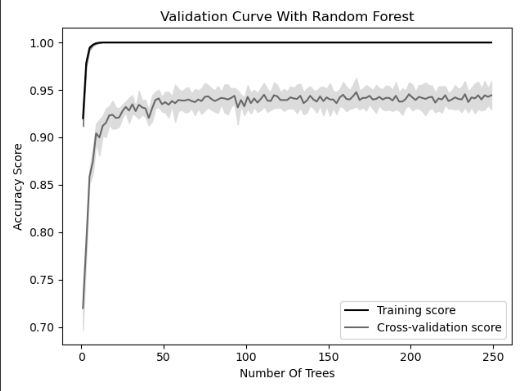
- 我们通过
validation curve来展示了不同决策树数量对于最后准确度的影响
- 当我们有少量的树时,训练和交叉验证的分数都很低,这表明模型拟合不足。
- 随着树的数量增加到 250 棵,两者的准确性都趋于平稳,这表明训练大规模森林的计算成本可能没有太大价值。
validation_curveparam_name:超参数的名称param_range:超参数的范围scoring:评估的方式和之前一样:accuracy、precision等等