BP神经网络 MATLAB实验报告
实验三 BP****神经网络
一、实验目的
掌握BP神经网络相关理论基础;
掌握BP神经网络的创建、训练及测试;
能够利用BP神经网络对数据进行分类。
二、实验内容
有60个数据,包含两个类别,每个数据有99个特征,前40个数据的类别标签为
label=[1 2 1 1 1 1 1 1 1 1
1 1 2 1 1 1 2 1 1 2
2 2 2 2 2 2 2 1 2 2
2 2 1 2 2 2 2 1 2 1]
用BP神经网络对后20个数据进行分类,实验数据见TD.txt文档。
三、实验步骤及实验内容(对实验步骤及实验内容、采用的参数进行详细阐述)
神经网络是机器学习中一种常见的数学模型,通过构建类似于大脑神经突触联接的结构,来进行信息处理。在应用神经网络的过程中,处理信息的单元一般分为三类:输入单元、输出单元和隐含单元。
输入单元是指输入的特征个数,在本实验中每个数据本身具有114个特征,故输入层应当是一个含有114个特征的向量。
本次分类数据类型在1和2之间,是二分类,本次输出的单元应当为一个数,此数的大小代表了数据的类别。
隐含单元是在输入与输出单元之间的单元,其作用是增加神经网络的参数量,通过调参得到更接近实际分类的输出结果。
本次实验为二分类,下面我们首先采用预测的方法对数据进行预测,进而进行分类。
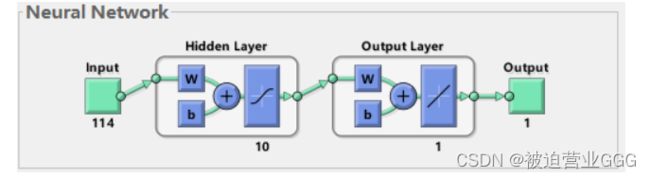
如下图是网络的结构:
设计的网络是一个114输入,隐藏层中含有10个神经元个数,1个输出的网络结构。
下面我们来分步进行神经网络的构建。
1、 构造数据集
题设给出的数据在TXT文件中,我们打开TXT文件查看:
上图是部分txt文件内容,我们看到,每一行的首个数字代表了行号,每一行中的其他114个数据代表了114个特征值。
我们再拉到txt文件的最后查看:
此为前40个数据的标签。
我们可以选择将数据复制进matlab中。但为了方便以后可能的数据修改,我们采用matlab的load函数对txt文件进行导入。在此之前,需要把标签放置到另一个label文件中,并将他俩放置在matlab的当前目录下,相对引用文件路径,有如下代码:
data=load(‘./TD.txt’);
label=load(‘./label.txt’)
导入数据后我们对数据集进行设置。
我们知道数据集分为训练数据集与测试数据集,由于共有40个有标签的数据,我们人为地将其分为30个训练数据,10个测试数据。
同时,为了得到本次实验的结果,我们一并设置最终20个未知标签数据的输入格式,如下:
pre=data(41:60,2:115)';%未知数据
input_train = input(1:30,2:115)'; %训练集data
output_train =output(:,1:30); %训练集label
input_test = input(31:40,2:115)';
output_test =output(:,31:40);
2、 构建网络
神经网络的构建需要定义输入层神经元个数,输出层个数,并自行定义隐藏层神经元数量。由于输入为114个节点,输出为1节点,故我们可以设置隐藏层为10个节点。
3、 样本的数据归一化
样本数据的归一化可以使得样本与标签均在[-1,1]之间,但此步骤也不一定能使得训练结果更准确。
在归一化的过程中,我们需要分别归一化训练集,测试集,未知集数据。
4、 网络创建
Newff函数进行神经网络的创建。输入输入层个数,输出层个数,隐藏层个数,输入层至隐藏层采用tansig双极性S函数,隐藏层至输出层采用purelin纯线性函数进行输出。采用梯度下降法与牛顿法trainlm进行训练。
5、 网络参数配置
配置参数,epoch,学习率,训练目标即最小误差。
6、 神经网络训练
net=train(net,inputn,outputn);进行训练。
7、 测试样本归一化
由于先前训练样本进行了归一化操作,为了保持量纲一直,测试数据应当也进行归一化操作。
8、 测试输出反归一化与输出误差
将归一化的测试数据放置到网络中进行预测,预测结果当然是归一化的结果,故真实结果需要对得出的结果label进行还原。此处还原需要采用起先label归一化时得到的参数进行反归一化,若用错则会导致输出出错。
测试集得到结果后与真实的10个label进行比较绘图,得到测试结果与训练率。
9、 预测
接着对未知的20个样本进行预测操作,预测过程同测试集预测过程,得到结果。
由于最终样本需要是2分类,在0与1之间,故需要对训练出来的结果进行二分类。训练label为1,2.故我们规定预测值大于1.5为2,预测值小于1.5为1。
四、代码(调用库函数,详细分析参数及返回值)
%data=load('D:\建模美赛\图像处理\BP神经网络\TD.txt'); %绝对引用
%%第一步 读取数据
data=load('./TD.txt');%相对引用
label=load('./label.txt')
input=data; %载入输入数据
output=label; %载入输出数据
%% 第二步 设置训练数据和预测数据
% 将指标变为列向量
pre=data(41:60,2:115)';
input_train = input(1:30,2:115)'; %训练集data
output_train =output(:,1:30); %训练集label
input_test = input(31:40,2:115)';
output_test =output(:,31:40);
%节点个数
inputnum=114; % 输入层节点数量
hiddennum=10; % 隐含层节点数量
outputnum=1; % 输出层节点数量
%% 第三本 训练样本数据归一化
[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间,inputps用来作下一次同样的归一化
[outputn,outputps]=mapminmax(output_train);
[pren,pres]=mapminmax(pre);
%% 第四步 构建BP神经网络
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');% 建立模型,传递函数使用purelin,采用梯度下降法训练
W1= net. iw{1, 1}; %输入层到中间层的权值
B1 = net.b{1}; %中间各层神经元阈值
W2 = net.lw{2,1}; %中间层到输出层的权值
B2 = net. b{2}; %输出层各神经元阈值
%% 第五步 网络参数配置( 训练次数,学习速率,训练目标最小误差等)
net.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.00001
%% 第六步 BP神经网络训练
net=train(net,inputn,outputn);%开始训练,其中inputn,outputn分别为输入输出样本
%% 第七步 测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps); % 对样本数据进行归一化
%% 第八步 BP神经网络预测
an=sim(net,inputn_test); %用训练好的模型进行仿真
%% 第九步 预测结果反归一化与误差计算
test_simu=mapminmax('reverse',an,outputps); %把仿真得到的数据还原为原始的数量级
test_simu=(test_simu>1.5)+1
error=test_simu-output_test; %预测值和真实值的误差
%%第十步 真实值与预测值误差比较
figure('units','normalized','position',[0.119 0.2 0.38 0.5])
plot(output_test,'bo-')
hold on
plot(test_simu,'r*-')
hold on
plot(error,'square','MarkerFaceColor','b')
legend('期望值','预测值','误差')
xlabel('数据组数')
ylabel('样本值')
title('BP神经网络测试集的预测值与实际值对比图')
[c,l]=size(output_test);
MAE1=sum(abs(error))/l;
MSE1=error*error'/l;
RMSE1=MSE1^(1/2);
disp(['-----------------------误差计算--------------------------'])
disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下:'])
disp(['平均绝对误差MAE为:',num2str(MAE1)])
disp(['均方误差MSE为: ',num2str(MSE1)])
disp(['均方根误差RMSE为: ',num2str(RMSE1)])
pre=mapminmax('apply',pre,pres);
res=sim(net,pre);
result=mapminmax('reverse',res,outputps);%还原
result=(result>1.5)+1
五、实验结果与分析(结果截图并对结果进行详细分析)
1、测试集预测的结果如下:
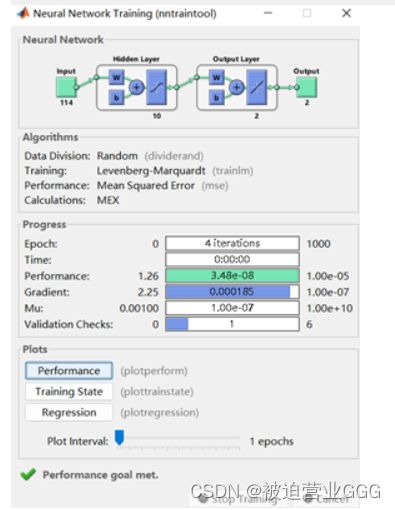
由于每次训练的不同,10个测试数据一般准确个数为9或10。上左图为某次训练的测试集结果,右图为训练的各项信息,我们可以看到训练速度极快,表现率也好。
2、采用训练好的模型对剩下20项进行分类预测,得到结果:
Result=[2 2 1 1 1 1 1 1 2 2 1 1 2 1 1 1 2 1 1 1]
六、问题与解决方法、总结。
1、在代码实现过程中,由于训练时对训练数据进行了归一化处理,那么在测试时应当也对目标进行归一化处理,以保证训练数据与测试数据处于同一量纲。此外,由于训练时也对目标label进行了量纲处理,故在测试集测试出结果后也应当对量纲进反归一化处理,即采用初始处理label的归一化参数对得到的参数进行反归一化。否则结果将会出现错误。
2、其实本次实验是分类网络,但由于是二分类,且采用的激活函数等与预测网络类似,故本次实验尝试了采用预测网络对目标进行分类。只是在最后处理结果时加上了人为的1.5阈值标定。从结果上看,分类结果优异。但另一方面,若复杂的特征数据进行分类时,或进行大于二分类的多分类数据时,人为的1.5阈值标定或其他人为标定将会导致目标结果的不确定化。即我可以将阈值设置为1.5,可以将阈值设置为2……这样将会导致结果有较强的主观性。故本次实验我还进行了标准的分类网络操作。
分类网络不同于预测网络的是,其将一个label标签变作类似[0 1]组合的数组,以标定分类结果。
现给出代码:
%data=load('D:\建模美赛\图像处理\BP神经网络\TD.txt'); %绝对引用
%%第一步 读取数据
data=load('./TD.txt');%相对引用
label=load('./label.txt')
input=data; %载入输入数据
output=zeros(2,40);
for i=1:40
switch label(i)
case 1
output(:,i)=[1; 0 ];
case 2
output(:,i)=[0 ;1 ];
end
end
%% 第二步 设置训练数据和预测数据
% 将指标变为列向量
pre=data(41:60,2:115)';
input_train = input(1:30,2:115)'; %训练集data
output_train =output(:,1:30); %训练集label
input_test = input(31:40,2:115)';
output_test =output(:,31:40);
%节点个数
inputnum=114; % 输入层节点数量
hiddennum=10; % 隐含层节点数量
outputnum=2; % 输出层节点数量
%% 第三本 训练样本数据归一化
[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间,inputps用来作下一次同样的归一化
[pren,pres]=mapminmax(pre);
%% 第四步 构建BP神经网络
net=newff(inputn,output_train,hiddennum,{'tansig','purelin'},'trainlm');% 建立模型,传递函数使用purelin,采用梯度下降法训练
W1= net. iw{1, 1}; %输入层到中间层的权值
B1 = net.b{1}; %中间各层神经元阈值
W2 = net.lw{2,1}; %中间层到输出层的权值
B2 = net. b{2}; %输出层各神经元阈值
%% 第五步 网络参数配置( 训练次数,学习速率,训练目标最小误差等)
net.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.00001
%% 第六步 BP神经网络训练
net=train(net,inputn,output_train);%开始训练,其中inputn,outputn分别为输入输出样本
%% 第七步 测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps); % 对样本数据进行归一化
%% 第八步 BP神经网络预测
an=sim(net,inputn_test); %用训练好的模型进行仿真
[c,d]=max(an);%输出最大下标
correct=sum(d==label(31:40))/10
%% 第九步 预测结果反归一化与误差计算
pre=mapminmax('apply',pre,pres);
res=sim(net,pre);
[c1,d1]=max(res);%输出最大下标
可见,在原始标签处理处与预测网络有所不同,然而网络的基本架构以及输入的特征量,隐藏层数量可以类似于预测网络。
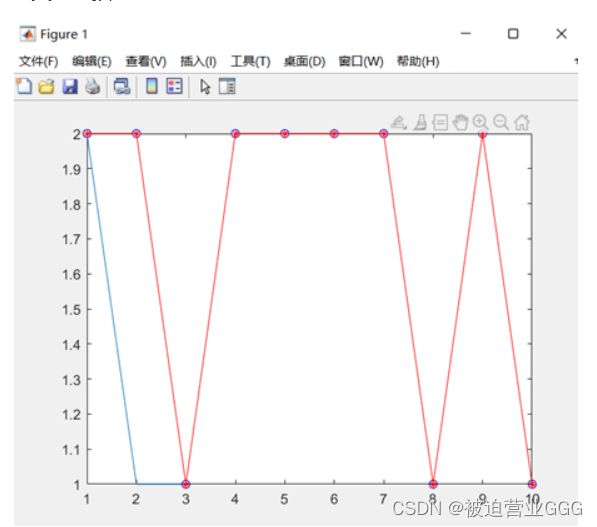
上左图为分类网络测试集的测试结果,右图为网络的架构。
对于未知label的数据进行分类,得到以下结果:
Result=[2 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 2 1]
对比预测网络:
Result=[2 2 1 1 1 1 1 1 2 2 1 1 2 1 1 1 2 1 1 1]
结果大致相同,可见预测网络和分类网络对于二分类的预测结果差别不大,均可用于二分类测试。
事实上,分类与预测是神经网络的两个分支,分类是在预测的基础之上将单个预测结果变为以0,1表示的多维数据,每个数据的点表示为结果为该类的概率。对于简单的二分类而言,网络架构相同的情况下,分类网络与预测网络差别不大。