线性模型 机器学习第三章
线性模型
文章目录
- 线性模型
- 前言
- 一、基本形式
- 二、线性回归
- 三、对数几率回归
-
- 1、应用背景:
- 2、概念及推导
- 3、求解参数w和b
- 四、线性判别分析
-
- 1、概念
- 2、实现
- 五、多分类学习
- 六、类别不平衡问题
- 总结
前言
一、基本形式
以西瓜问题来说,根据其属性判定,判定一个西瓜的好坏。
f(一个西瓜)= w1 · 西瓜属性1 + w2 · 西瓜属性2 +……+ wd · 西瓜属性d,
好瓜 or 坏瓜 = 0.2 · 色泽 + 0.5 · 根蒂 +…… + 0.1· 条纹
给定有d个属性描述的示例x=(x1;x2;…;xd),其中xi是x在第i个属性上的取值,线性模型试图学得一个通过属性的线性组合来进行预测的函数。(对于一个有d个属性的样本,线性模型希望和线性函数一样,能得到一个形如 y=ax+b的式子,只不过此时x是一个多属性的,可看成一个向量)即
一般用向量形式写成
二、线性回归
线性回归: 试图学得一个线性模型以尽可能准确的预测实值输出标记。(希望学得一个线性函数预测样本x的真实值y)
给定数据集D={(x1,y1),(x2,y2),……,(xm,ym)},其中xi = (xi1;xi2;…;xid),yi ∈R。假设样本x仅有一个属性(方便讨论),线性回归试图学得
对于线性回归,有w和b两个参数需要确定,回归任务中常用的性能度量是均方误差,我们通过最小化均方误差来获得w和b。
均方误差对应了欧几里得距离(简称欧氏距离,公式详情请看欧氏距离)。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中,最小二和曾发就是试图找到一条直线,是所有样本到直线上的欧氏距离之和最小。
求解w和b使得均方误差 E ( w , b ) = ∑ i = 1 n ( y i − w x i − b ) 2 E_(w,b)=\sum_{i=1}^{n}(y_i - wx_i - b)^2 E(w,b)=∑i=1n(yi−wxi−b)2 最小化的过程,称为线性回归模型的最小二乘“参数估计”。将 E ( w , b ) E_(w,b) E(w,b)分别对w和b求导,得到
∂ E ( w , b ) ∂ w = 2 ( ∑ i = 1 m ( y i − w x i − b ) ⋅ ( − x i ) ) = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) \frac{∂E_(w,b)}{∂w} = 2( \sum_{i=1}^{m}(y_i -wx_i - b) ·(-x_i)) = 2(w\sum_{i=1}^{m}x_i^2 - \sum_{i=1}^{m}(y_i - b)x_i) ∂w∂E(w,b)=2(∑i=1m(yi−wxi−b)⋅(−xi))=2(w∑i=1mxi2−∑i=1m(yi−b)xi)
∂ E ( w , b ) ∂ b = 2 ( ∑ i = 1 m ( y i − w x i − b ) ⋅ ( − 1 ) ) = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) \frac{∂E_(w,b)}{∂b} = 2( \sum_{i=1}^{m}(y_i -wx_i - b) ·(-1) ) = 2(mb - \sum_{i=1}^{m}(y_i - wx_i)) ∂b∂E(w,b)=2(∑i=1m(yi−wxi−b)⋅(−1))=2(mb−∑i=1m(yi−wxi))
令上述偏导=0,得到以下公式,求出w和b。
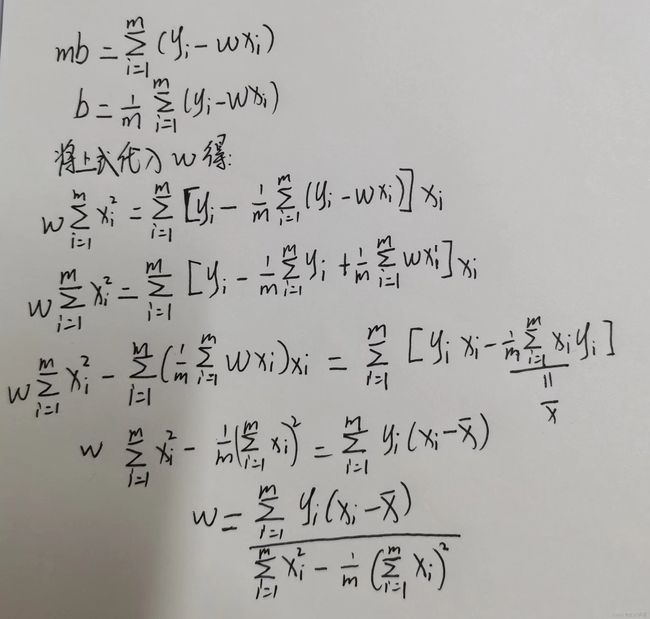
上述讲解是样本仅有一个属性,对应的也只有一个w系数。但是常见为x为多元属性,有d个属性描述,此时对应有d个w,此时,我们试图学得
类似的,使用最小二乘法,对w和b进行估计。为便于讨论,将w和b写为向量形式, w ^ \widehat {w} w =(w;b),相应的把数据集d表示为一个m x (d + 1)大小的矩阵X,其中每一行对应一个样本(示例),每行前d个元素对应于示例的d个属性值,最后一个元素恒为1,如下图所示:
再把标记写为向量形式y=(y1;y2;…;ym)
类似的,求解 w ^ \widehat {w} w ,根据均方误差公式,令 E w ^ = ( y − X w ^ ) T ( y − X w ^ ) E_{\widehat {w}} = (y - X{\widehat {w}})^T(y - X{\widehat {w}}) Ew =(y−Xw )T(y−Xw ),对 w ^ \widehat {w} w 求偏导得到
∂ E w ^ ∂ w ^ = 2 X T ( X w ^ − y ) \frac{∂E_{\widehat {w}}}{∂\widehat {w}} = 2 X^T(X{\widehat {w}} - y) ∂w ∂Ew =2XT(Xw −y)
简单地,当 X T X X^TX XTX为满秩矩阵或正定矩阵时,令上述偏导为0,可得 w ^ \widehat {w} w 的极值 w ^ \widehat {w} w *,为
w ^ ∗ = ( X T X ) − 1 X T y \widehat {w}* = (X^TX)^{-1}X^Ty w ∗=(XTX)−1XTy
其中 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1是矩阵 X T X X^TX XTX的逆矩阵,令 x ^ i = ( x i ; 1 ) \widehat {x}_i = (x_i;1) x i=(xi;1),则最终学得的多元线性回归模型为:
f ( x ^ i ) = x ^ i T ( X T X ) − 1 X T y f(\widehat {x}_i) = \widehat {x}_i^T(X^TX)^{-1}X^Ty f(x i)=x iT(XTX)−1XTy
上述公式看起来很麻烦,在这里还原为原公式,便于理解。
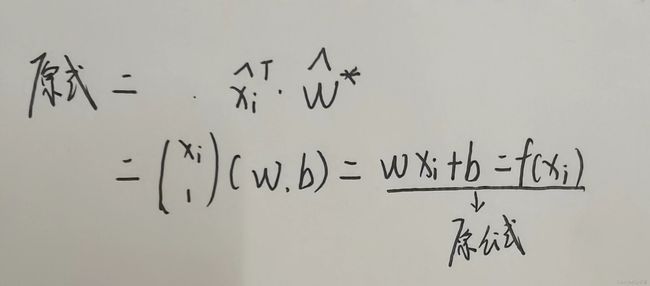
广义线性模型:
首先,将线性回归模型简写为,y = wTx +b形式,
令模型预测值逼近y的衍生函数,假设有单调可微函数g(·),即g(y)= wTx +b。(此时在形式上,仍是线性回归,但是实质上是求输入空间x到输出空间y的非线性映射。)
变换形式后,得 y = g − 1 ( w T x + b ) y = g^{-1}(w^Tx + b) y=g−1(wTx+b)
这样的模型就称为广义线性模型,其中函数g(·)称为“联系函数”。
对数线性回归:
是广义线性回归在g(·)= ln(·)时的特例。形式如下:
l n y = w T x + b lny = w^Tx + b lny=wTx+b
三、对数几率回归
1、应用背景:
之前讨论的都是使用线性模型进行回归学习,但是要做分类任务,则需联系上节广义线性模型,找到一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。对二分类任务,其输出标记y∈{0,1},只有两种取值,非此即彼,但是线性回归模型成圣的预测值(z=wTx +b)是一个实值。我们需要将实值转换为0 or 1 值。理想情况下是单位阶跃函数。如下图所示,红色为阶跃函数。
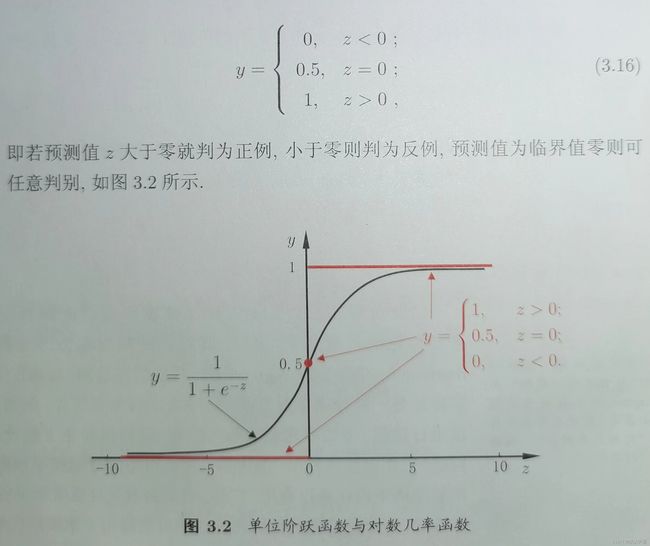
可从图中看出,单位阶跃函数不连续,不能直接用作广义线性模型的 g − 1 ( ⋅ ) g^{-1}(·) g−1(⋅)函数,我们希望找到能够在一定程度上近似单位阶跃函数的、单调可微的“替代函数”,对数几率函数就是这样的一个常用替代函数: y = 1 1 + e − z y=\frac1{1+e^{-z}} y=1+e−z1
从图中可看出,对数函数是一种“Sigmoid函数”,它将z值转换为一个接近0或1的y值,并且其输出值在z=0附近变化很陡。
2、概念及推导
将对数几率函数作为 g − 1 ( ⋅ ) g^{-1}(·) g−1(⋅)带入广义线性模型,得到: y = 1 1 + e − ( w T x + b ) y=\frac1{1+e^{-(w^Tx + b)}} y=1+e−(wTx+b)1

其中,若将y视为样本x为正例的可能性,则1-y是其为反例的可能性,两者的比值 y 1 − y \frac y{1-y} 1−yy 称为几率,反映了x作为正例的可能性。对几率取对数得到对数几率: l n y 1 − y ln\frac y{1-y} ln1−yy
从图中可以看出,实际是在用线性回归模型的预测结果 w T x + b w^Tx + b wTx+b去逼近真实标记的对数几率 l n y 1 − y ln\frac y{1-y} ln1−yy ,因此对应的模型称为“对数几率回归”。
注意:
虽然对数几率回归名为回归,实际是一种分类学习方法。
对数几率函数的优点: 1. 直接对分类可能性建模,无需事先假设数据分布,避免假设分布不准确带来的问题
2. 不是仅预测出类别,而是可得到近似概率预测,对许多需利用概率辅助决策的任务很有用。
3. 对数几率函数是任意阶可导的凸函数,有很好的的数学性质,现有的许多数值最优化算法都可直接用于求解最优解。
3、求解参数w和b
由上节对数几率函数进行化简可得:
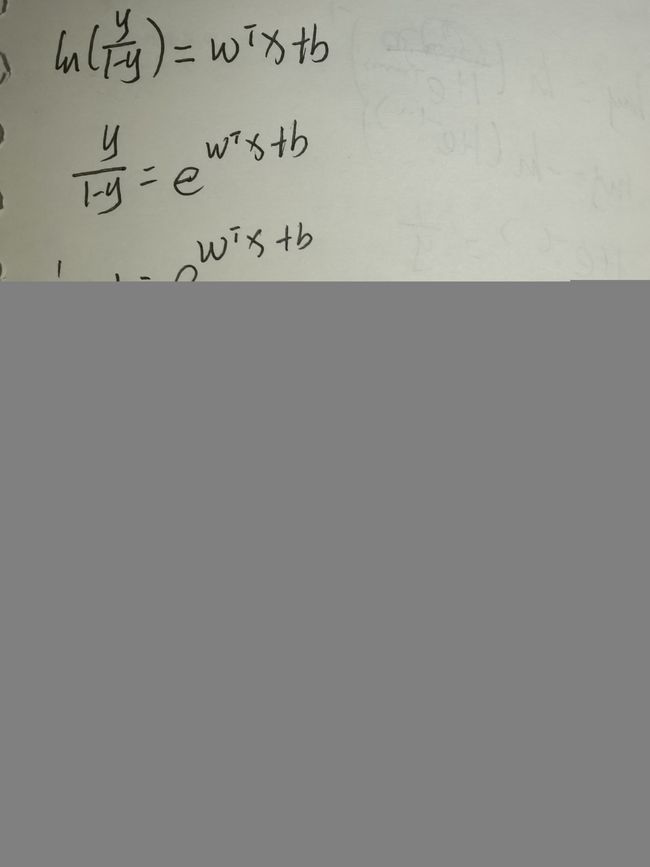
y = e w T x + b e w T x + b + 1 y = \frac {e^{w^Tx + b}}{e^{w^Tx + b}+1} y=ewTx+b+1ewTx+b,1-y = 1 e w T x + b + 1 \frac 1{e^{w^Tx + b}+1} ewTx+b+11
将对数几率函数中的y视为类后验概率估计p(y = 1 | x),可将其重写为
l n p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = w T x + b ln \frac {p(y = 1 | x)}{p(y = 0 | x)} = w^Tx + b lnp(y=0∣x)p(y=1∣x)=wTx+b
对应的,
p ( y = 1 ∣ x ) = e w T x + b e w T x + b + 1 p(y = 1 | x) = \frac {e^{w^Tx + b}}{e^{w^Tx + b}+1} p(y=1∣x)=ewTx+b+1ewTx+b
p ( y = 0 ∣ x ) = 1 e w T x + b + 1 p(y = 0 | x) = \frac1{e^{w^Tx + b}+1} p(y=0∣x)=ewTx+b+11
我们可以通过“极大似然法”来估计w和b。详情点击极大似然估计.给定数据集D={(x1,y1),(x2,y2),……,(xm,ym)},对数几率回归模型最大化“对数似然”:
l ( w , b ) = ∑ i = 1 m l n p ( y i ∣ x i ; w , b ) l(w,b) = \sum_{i=1}^mln p(y_i|x_i;w,b) l(w,b)=∑i=1mlnp(yi∣xi;w,b)
即,令每个样本属于其真实标记的概率越大越好。
(后续求解涉及最优化理论,暂时省略,需要的可以催更这部分)
四、线性判别分析
1、概念
线性判别分析(简称LDA)是一种经典的线性学习方法,也称Fisher判别分析。
思想:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的未知来确定新样本的类别。
给定数据集 D = { ( x i , y i ) } i = 1 m , y i ∈ D=\{(x_i,y_i)\}_{i=1}^m,y_i ∈ D={(xi,yi)}i=1m,yi∈{0,1},有以下概念:
X i X_i Xi:第i类示例的集合(i∈{0,1})
μ i μ_i μi:第i类示例的均指向量
∑ i \sum_i ∑i:第i类示例的协方差矩阵
若将数据投影到直线w上,则两类样本的中心在直线上的投影分别为 w T μ 0 和 w T μ 1 w^Tμ_0和w^Tμ_1 wTμ0和wTμ1;若将所有样本都投影到直线上,则两类样本的协方差分别为 w T ∑ 0 w 和 w T ∑ 1 w w^T\sum_0w和w^T\sum_1w wT∑0w和wT∑1w。(由于直线是一维空间,因此 w T μ 0 、 w T μ 1 w^Tμ_0、w^Tμ_1 wTμ0、wTμ1、 w T ∑ 0 w 、 w T ∑ 1 w w^T\sum_0w、w^T\sum_1w wT∑0w、wT∑1w都是实数)
我们提到LDA思想是“使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离”,同类尽可能接近,可以让同类样例投影点的协方差尽可能小,即 w T ∑ 0 w + w T ∑ 1 w w^T\sum_0w+w^T\sum_1w wT∑0w+wT∑1w尽可能小;异类尽可能远离,可以让类中心之间的距离尽可能大,即 ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 ||w^Tμ_0 - w^Tμ_1||_2^2 ∣∣wTμ0−wTμ1∣∣22,同时考虑上述两种情况,则可以得到最大化目标J:
J = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T ∑ 0 w + w T ∑ 1 w J = \frac{||w^Tμ_0 - w^Tμ_1||_2^2}{w^T\sum_0w+w^T\sum_1w} J=wT∑0w+wT∑1w∣∣wTμ0−wTμ1∣∣22
化简后得 = w T ( μ 0 − μ 1 )( μ 0 − μ 1 ) T w w T ( ∑ 0 + ∑ 1 ) w \frac{w^T(μ_0 - μ_1)(μ_0 - μ_1)^Tw}{w^T(\sum_0+\sum_1)w} wT(∑0+∑1)wwT(μ0−μ1)(μ0−μ1)Tw
定义“类内散度矩阵”:
S w = ∑ 0 + ∑ 1 S_w = \sum_0+\sum_1 Sw=∑0+∑1
= ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 0 ) ( x − μ 0 ) T = \sum_{x∈X_0}(x - μ_0)(x - μ_0)T + \sum_{x∈X_1}(x - μ_0)(x - μ_0)T =∑x∈X0(x−μ0)(x−μ0)T+∑x∈X1(x−μ0)(x−μ0)T
定义“类间散度矩阵”:
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b= (μ_0 - μ_1)(μ_0 - μ_1)T Sb=(μ0−μ1)(μ0−μ1)T
LDA最大化目标(此时也称Sb与Sw的“广义瑞利商”)可重写为:
J = w T S b w w T S w w J = \frac{w^TS_bw}{w^TS_ww} J=wTSwwwTSbw
2、实现
求解w:
重写后的最大化目标中的分子分母都是关于w的二次项,J的解与w的长度无关,只与w的方向有关。令 w T S w w = 1 w^TS_ww = 1 wTSww=1,最大化目标等价于
m i n w − w T S b w min_w \ \ -w^TS_bw minw −wTSbw
s . t . w T S w w = 1 s.t. \ \ \ \ \ \ \ \ w^TS_ww = 1 s.t. wTSww=1
由拉格朗日乘子法,上式等价于
S b w = λ S w w S_bw = λS_ww Sbw=λSww
其中, λ是拉格朗日乘子,注意到 S b w S_bw Sbw的方向恒为μ0 - μ1,令
S b w = λ ( μ 0 − μ 1 ) S_bw = λ(μ_0 - μ_1) Sbw=λ(μ0−μ1)
代入上式可得, S w w = ( μ 0 − μ 1 ) , w = S w − 1 ( μ 0 − μ 1 ) S_ww=(μ_0 - μ_1),w=S_w^{-1}(μ_0 - μ_1) Sww=(μ0−μ1),w=Sw−1(μ0−μ1)
S w − 1 S_w^{-1} Sw−1求解:通常通过对 S w S_w Sw进行奇异值分解,即 S w = U ∑ V T S_w=U∑V^T Sw=U∑VT,∑是一个实对角矩阵,其对角线上的元素是 S w S_w Sw的奇异值,由 S w − 1 = V ∑ − 1 U T S_w^{-1} = V∑^{-1}U^T Sw−1=V∑−1UT解得 S w − 1 S_w^{-1} Sw−1
LDA可从贝叶斯决策理论的角度来阐释,并可证明,当两类数据同先验、满足高斯分布且协方差相等时,LDA可达到最优分类。
可将LDA推广到多分类任务中,这里暂时省略,需要时,我会再更。
五、多分类学习
对多分类学习任务,基本思路为“拆解法”,将多分类任务拆解为若干个二分类任务求解。本节主要讲解拆分策略。
对给定数据集D={(x1,y1),(x2,y2),……,(xm,ym)},yi∈{C1,C2,…,CN},有以下情况:
| 经典拆分策略 | 一对一 | 一对多 | 多对多 |
| 英文 | One vs. One(简称OvO) | One vs. Rest(简称OvR) | Many vs. Many (简称MvM) |
| 策略内容 | OvO将N个类别两两配对,从而产生N(N-1)/ 2个分类任务,测试阶段,新样本将同时提交给所有分类器,得到N(N-1)/ 2个分类结果,预测的最多的类别作为最终分类结果 | 每次将一个类别作为正例,其他类作为一个反例的整体,对应的类别标记作为最终分类结果。若有多个分类器预测为正类,选择置信度最大的类别标记作为分类结果 | 每次将若干个类作为正类,若干个其他类作为反类(OvO和OvR是其特例)。MvM的正、反类构造必须有特殊的设计,不能随意选取。常用技术:“纠错输出码(简称ECOC)”。 |
| 比较 | 需训练N(N-1)/ 2个分类器 储存开销和测试时间开销较大 训练时间通常较小 |
需训练N个分类器 储存开销和测试时间开销较小 训练时间通常较大 |
下文将对编码进行详细讲解 |
- 编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可以训练出M个分类器。
- 解码:M个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
编码示意图(先欠着)
类别划分通过“编码矩阵”指定。编码矩阵有多种形式,常见有二元码和三元码。
六、类别不平衡问题
类别不平衡问题:就是指分类任务中不同类别的训练样例数目差别很大的情况。
类别不平衡学习的一个基本策略——“再缩放”:
公式: y ′ 1 − y ′ = y 1 − y × m − m + \frac {y'}{1-y'} = \frac y{1-y} × \frac {m^-}{m^+} 1−y′y′=1−yy×m+m−
当类别平衡时,分类器决策规则为 y 1 − y > 1 \frac y{1-y} >1 1−yy>1则预测为正例。
当类别不平衡时,令 m + m^+ m+表示正例数目, m − m^- m−表示反例数目,观测几率是 m − m + \frac {m^-}{m^+} m+m−,我们通常假设训练集是无偏采样,观测几率=真实几率。只要分类器的预测几率高于观测几率就应判定为正例,即 y 1 − y > m − m + \frac y{1-y} > \frac {m^-}{m^+} 1−yy>m+m−。
此时,采用再缩放策略,使得正反例数进行调整,判定 y ′ 1 − y ′ \frac {y'}{1-y'} 1−y′y′>1是否成立,此时 y ′ 1 − y ′ = y 1 − y × m − m + \frac {y'}{1-y'}=\frac y{1-y} × \frac {m^-}{m^+} 1−y′y′=1−yy×m+m−
方法:(假设正例数远远小于反例数)
1.直接对训练集里的反类样例进行“欠采样”,即去除一些反例,使得正反例数目相接近。
2.对训练集里的正类样例进行“过采样”,即增加一些正例,使得正反例数目相接近。
3.直接基于原始训练集进行学习,但在用训练好的分类器进行与测试,将公式嵌入器决策过程中,称为“阈值移动”。
“再缩放”也是“代价敏感学习”的基础。在代价敏感学习中将再缩放公式中 m + / m − m^+/m^- m+/m−用 c o s t + / c o s t − cost^+/cost^- cost+/cost−代替即可。其中, c o s t + cost^+ cost+是将正例误分为反例的代价, c o s t − cost^- cost−是将反例误分为正例的代价。
总结
本章主要讲解了线性模型,我们要知道线性模型的本质就是寻找一个函数,使其能够符合训练集规律(在训练集上学习),又能尽可能正确预测未见过的数据(泛化能力强)。