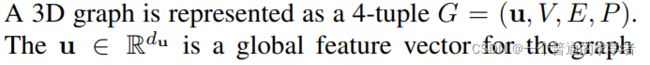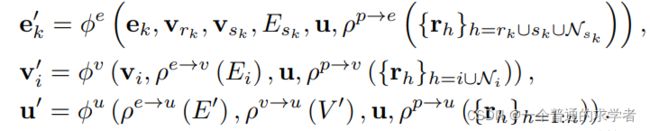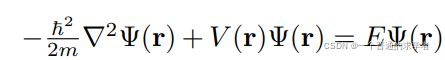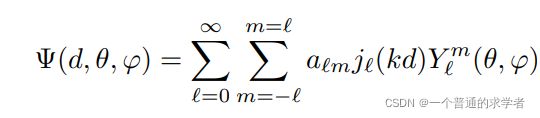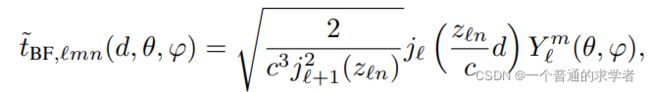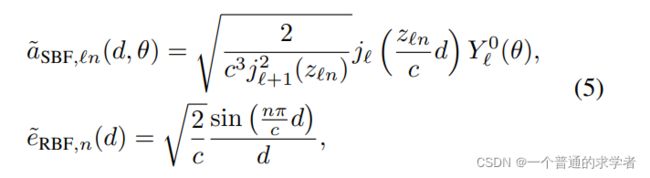浅谈Spherical Message Passing for 3D Graph Networks

目录

​背景

MPNN

SMPNN

Definition of Graph in paper

Computational Steps

Spherical message passing

New Computational Steps

Physical Solutions Approximating DFT

网络架构

Input Block

Interaction Block & Output Block

总结

参考

---

Background

对3D Graph的表征学习需要考虑到每个节点的位置信息，这是一个待探索的领域。文章中，作者提出将每个节点的位置信息加入到Message Passing中进行分子表征学习，名为3DGN，再进一步引入Spherical Coordinate System下的坐标三元组后成为SphereNet。

MPNN

首先需要了解以下什么是Message Passing。消息传递神经网络是谷歌在17年的一篇叫Neural Message Passing for Quantum Chemistry （点我跳转pdf）的文章中提出的，利用Message Passing来提取特征，首先化学分子很自然的可以看成一个图，键就是边，原子就是节点。

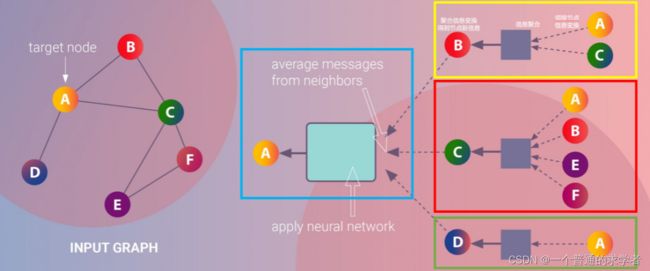
 这里借用一下别人的图，因为我觉得这个很好描述了消息传递机制！

消息传递分两个阶段：消息传递阶段以及读出阶段

在这里，把A节点看作receiver，那他的邻接点就要send信息给他，自然就是sender，想要从邻接点中get到信息，首先邻接点就需要有信息。用其中一个临界点B举例子，B又要从B的邻接点中get信息，也就是A和C，然后把A和C的信息聚合起来，作为B能send给A的信息，A将receive到所有信息后，通过nn，便可完成A本身特征的更新，传递阶段完成。

读出阶段其实就是利用每个节点更新的信息，把他们汇总经一个nn提取全局信息。

想要具体查看具体nn的实现点击【GNN】MPNN：消息传递神经网络

SMPNN

接下来就是文章的重点——球形消息传递神经网络

Definition of Graph in paper

我们知道，正常的Graph无非就是Node和Edge，但是文章说了3D Graph，自然要多点内容。

 他说3D Graph包含一个四元组——()，概括性的说分别对应全局特征，点，边，每个点的在笛卡尔坐标系的值。然后的话就是，里包括receiver和sender的索引，以及他们两个之间的边的特征，表示邻接点。有了这些概念，下面的就很好理解了。

Computational Steps

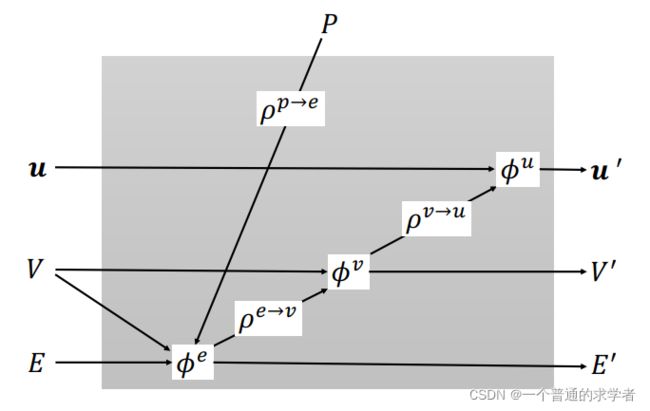
 看一下他的3DGN更新步骤叭。

是一个nn，是一个聚合函数。很明显了，更新边就是用原本的边特征，加两个点（receiver和sender），加sender的邻接点之间的边，再把上面涉及的点的位置信息聚合，一起丢到nn中，实现对的更新，下面的一样的，不过多赘述，不过获取其实就是MP的readout阶段。

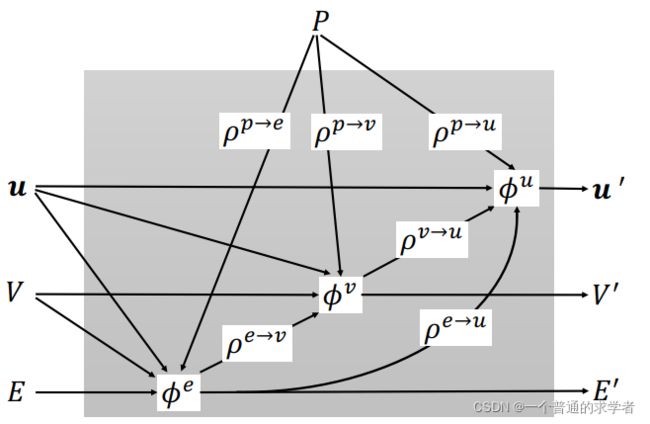
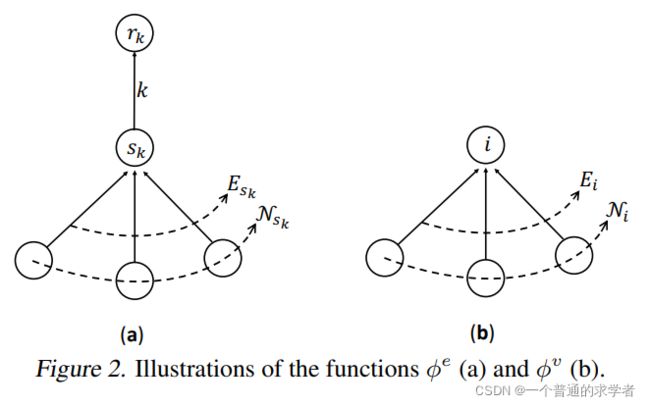
这个是更新图示，跟前面提到的差不多。 右图上面这个就相当于左图上面的，右图下面的一堆空白点就相当于左图的，右图是在更新边，左图是在更新点，emmmmmm，是这个意思。

Spherical message passing

这个图的意思是，以receiver和sender之间的边确定一个轴建立一个球面坐标系，得到一个三元组()，然后类似的，就可以像前面一样进行Message Passing了。注意看第二个图，这个的定义挺有意思的，它是按照逆时针的顺序，以前一个q建立参考平面，得到相对于前一个点的扭角，因此有。

作者说这样可以很好的表示3D位置信息，并且以一个双氧水分子为例子进行说明。

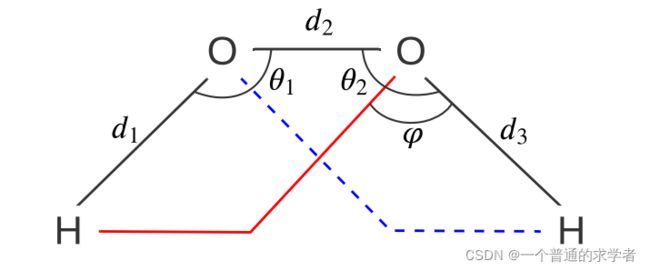 这个三元组对于辨识一个分子极其重要，特别是那个扭角（），当你扭动O-H键时，扭角变化，这个分子相对性质也会发生变化。

New Computational Steps

于是，作者把原本在笛卡尔坐标系中的点，搬到了球面坐标系，3DGN变成了SphereNet，更新步骤做了简化。

可以看到，把位置信息的聚合，只用在了更新边上，这样看起来其实更像一个递进的结构，更新边->更新点->更新全局特征，当然，这个位置信息由原来的笛卡尔坐标系值变为球面坐标系值，至于怎么嵌入到空间，别急。

Physical Solutions Approximating DFT

 这里说的是直接使用3D信息没有物理意义，所以考虑近似密度泛函理论(DFT)的薛定谔方程的解，属实是没看懂，但这里就是上面说到的把三元组嵌入到空间的步骤。

薛定谔方程 

转到球面坐标系下的解

 这三条式子没看懂，欸，但在网络架构中有用到。

Network Architecture

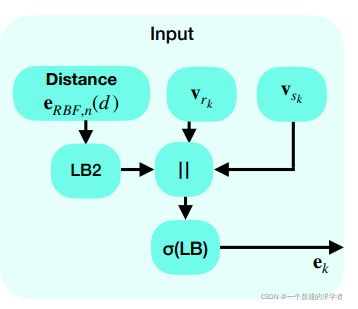
Input Block

这个是对边的初始化，也就是一开始赋予边的特征，LB2是两个线性层的意思，是激活函数，两个v自然就是两点的特征了。

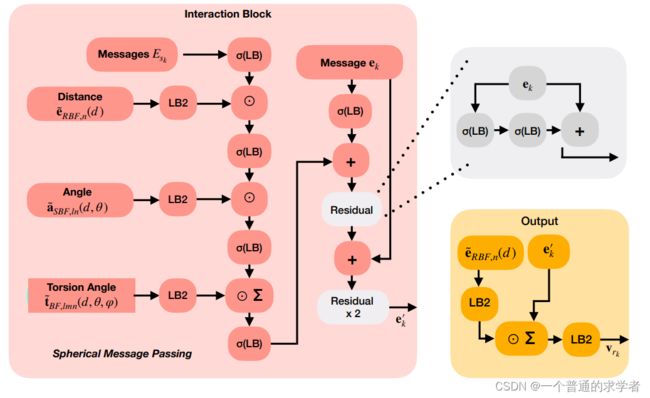
Interaction Block & Output Block

 这是边更新（Interaction Block）以及最后点更新（Output），可以看到前面提到的三个方程在这里用到了，就是把3D位置信息嵌入到空间中了，最后更新边，

Summary

这篇文章还是很值得一读的，17年那篇Neural Message Passing for Quantum Chemistry也值得一看，消息传递这个思想个人感觉比以往依靠只邻域聚合特征感受野更大。其次就是那个三元组的构建，前一个点作为参考平面建立扭角，这个还是特别有意思的。最近看的3D模型都用球面坐标来进行表征学习，或许这样能确实能提高学习的准确度。

Reference

[1]. 【GNN】MPNN：消息传递神经网络

[2].  ​​​​​​基于3D结构的球形消息传递机制的GNN Spherical Message Passing for 3D Graph Networks

[3]. 消息传递图神经网络

[4]. 论文笔记：Neural Message Passing for Quantum Chemistry

[5]. Neural Message Passing for Quantum Chemistry

[6]. Spherical Message Passing for 3D Graph Networks