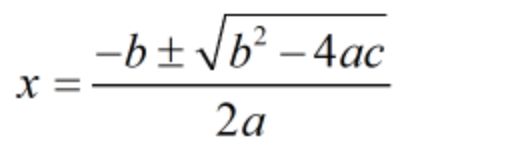人工智能：第三章 机器学习之逻辑回归

目标

这次学习的目标是：机器学习之逻辑回归，并用逻辑回归实现二分类的问题。

将通过三个实战项目理解和熟练掌握机器学习的逻辑回归模型

逻辑回归介绍

什么是逻辑回归

逻辑回归是用于解决分类问题的一种模型，根据数据特征或属性，计算其归属于某一类别的概率，根据概率值判断其所属类别。

主要应用的场景：二分类问题

下面介绍下flare老师对逻辑回归讲解的课件

逻辑回归求解

求解出损失函数的最小值，即可得到最优的逻辑回归模型

分类任务与回归任务的区别

逻辑回归实战准备

分类散点图可视化

逻辑回归模型使用

建立新的数据集

模型评估

任务介绍

实战一：考试通过预测

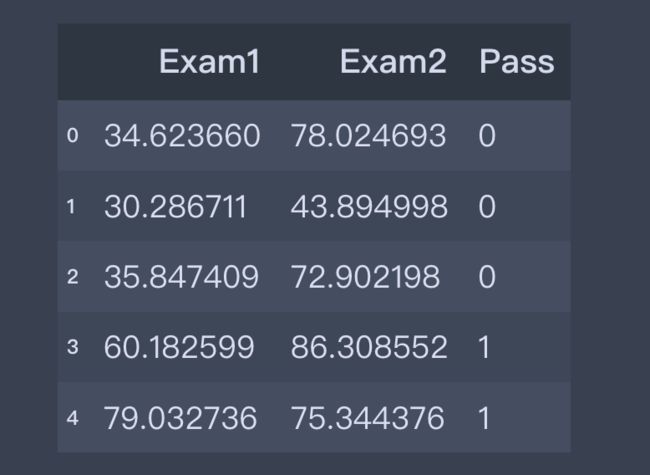
1、基于examdata.csv数据，建立逻辑回归模型，评估模型表现：

2、预测Exam1=75，Exam=60时，该同学能否通过Exam3

实战二：建立二阶边界函数，重新进行考试通过预测

建立二阶边界函数，重复任务实战一种的任务1和任务2

实战三：芯片质量预测

1、基于chip_test.csv数据，建立逻辑回归模型（二阶边界），评估模型表现；

2、以函数的方式求解边界曲线

3、描绘出完整的决策边界曲线

流程

1、导入数据

2、可视化分类数据散点图

3、生成新的特征数据并赋值

4、创建模型并训练

5、模型预测

6、评估模型的准确率

7、查看决策边界函数的各个系数

8、求解出边界曲线函数

9、可视化决策边界曲线

具体步骤

实战一：考试通过预测

1、导入文件数据

#load the data
import numpy as np
import pandas as pd
path='Desktop/artificial_intelligence/Chapter3/examdata.csv'
data=pd.read_csv(path)
data.head()

2、可视化数据

#visualize the data
from matplotlib import pyplot as plt
fig1=plt.figure()
plt.scatter(data['Exam1'],data['Exam2'])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.show()

3、添加mask标签

#add label mask
mask=data['Pass']==1
mask

取反值是~mask

~mask

取出当Pass标签为1的时候Exam1的数据

data['Exam1'][mask].head()

同理也可以的取出Exam2的数据和用～mask取出标签为0的时候的值

4、使数据分类展示

fig2=plt.figure()
passed=plt.scatter(data['Exam1'][mask],data['Exam2'][mask])
failed=plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

plt.legend是用来在图片里面添加图例的

5、赋值给X和y

X=data.drop('Pass',axis=1)
X.head()

y=data['Pass']


y.head()

x1=data['Exam1']
x2=data['Exam2']
print(X.shape)
print(y.shape)

(100, 2)

(100,)

6、建立模型并训练

from sklearn.linear_model import LogisticRegression
lr=LogisticRegression()
lr.fit(X,y)

7、预测结果并查看准确率

from sklearn.metrics import accuracy_score
y_predict=lr.predict(X)
print(y_predict.shape)
accuracy=accuracy_score(y,y_predict)
print(accuracy)

(100,)

0.89

8、预测给定的数据

预测Exam1=75，Exam=60时，该同学能否通过Exam3

y_test=lr.predict([[75,60]])
print(y_test)
print(type(y_test))
print('passed' if y_test==1 else 'failed')

[1]

passed

9、查看决策边界函数的各个theta系数

查看截距θ0，Exam1（x1）的系数θ1和Exam2（x2）的系数θ2

lr.intercept_

array([-25.05219314])

lr.coef_

array([[0.20535491, 0.2005838 ]])

theta0=lr.intercept_[0]
theta1=lr.coef_[0][0]
theta2=lr.coef_[0][1]
print(theta0)
print(theta1)
print(theta2)

-25.05219314274188

0.20535491217790378

0.20058380395469042

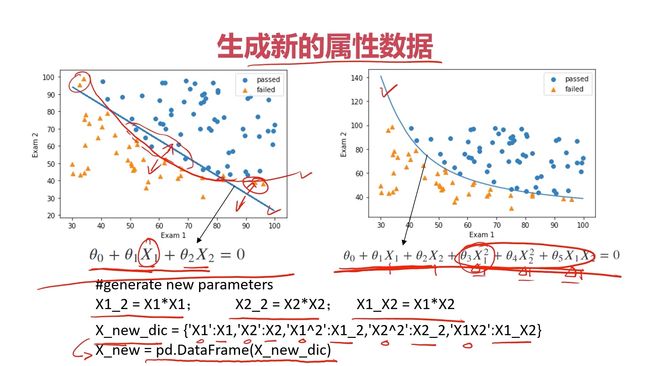
10、根据一阶决策边界函数，求出Exam2（x2）和Exam1（x1）的关系函数

一阶的决策边界函数式为：θ0+θ1*X1+θ2*X2=0

求出 X2=-(theta0+theta1*x1)/theta2

x2_new=-(theta0+theta1*x1)/theta2
x2_new

11、在分类散点图的基础上可视化决策边界线

fig3=plt.figure()
passed=plt.scatter(data['Exam1'][mask],data['Exam2'][mask])
failed=plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.legend((passed,failed),('passed','failed'))
plt.plot(x1,x2_new)
plt.show()

实战二：建立二阶边界函数，重新进行考试通过预测

二阶的决策边界函数式为：θ0+θ1*X1+θ2*X2+θ3*X1²+θ4*X2²+θ5*X1*X2=0

1、创建新的数据并赋值

x1_2=x1x1
x2_2=x2x2
x1_x2=x1x2
X_new={'x1':x1,'x2':x2,'x1x1':x1_2,'x2x2':x2_2,'x1x2':x1_x2}
X_new=pd.DataFrame(X_new)
X_new.head()

2、建立模型并用新数据训练

from sklearn.linear_model import LogisticRegression
lr2=LogisticRegression()
lr2.fit(X_new,y)

3、重新预测，并查看准确率

y2_predict=lr2.predict(X_new)
from sklearn.metrics import accuracy_score
score=accuracy_score(y,y2_predict)
score

1.0

可以看到正确率已经达到了100%

4、求解出x2对应的x1的函数关系

二阶的决策边界函数式为：θ0+θ1*X1+θ2*X2+θ3*X1²+θ4*X2²+θ5*X1*X2=0

根据高中的数学知识：ax²+bx+c=0中的求解x的方程式为x=[-b±√(b²-4ac)]/2a

式中√(b²-4ac)表示的是(b²-4ac)的平方根。只要(b²-4ac)大于0就有解

θ0+θ1*X1+θ2*X2+θ3*X1²+θ4*X2²+θ5*X1*X2=0可以变形为

θ4*X2²+(θ2+θ5*X1)*X2+( θ0+θ1*X1+ θ3*X1²)=0

进而求解出X2和X1的对应关系

5、对a、b、c分别赋值，求解方程式

把截距赋值给θ0

theta0=lr2.intercept_

查看θ1到θ5的系数

lr2.coef_

array([[-8.95942818e-01, -1.40029397e+00, -2.29434572e-04,

3.93039312e-03, 3.61578676e-02]])

可以看到得到的是一个二维数组

分别赋值给θ1到θ5

theta1=lr2.coef_[0][0]
theta2=lr2.coef_[0][1]
theta3=lr2.coef_[0][2]
theta4=lr2.coef_[0][3]
theta5=lr2.coef_[0][4]
print(theta1,'\n',theta2,'\n',theta3,'\n',theta4,'\n',theta5)

-0.8959428182503584

-1.400293968707803

-0.0002294345723632137

0.003930393115569492

0.03615786759876832

因为θ4*X2²+(θ2+θ5*X1)*X2+( θ0+θ1*X1+ θ3*X1²)=0

所以定义a，b，c为

a=theta4
b=theta2+theta5*x1
c=theta0+theta1*x1+theta3*x1*x1

虽然X2有两个解，但是在本案例中，因为考试分数都是正的，只取一个结果为正的即可。

调用np.sqrt是求一个数的平方根

x2_new==(-b+np.sqrt(b*b-4*a*c))/(2*a)

6、可视化前的排序

注意：在画x2_new和x1的图像的时候，x1需要先排序，因为不排序的话，样本中的x1是乱的。得到的就不是一条平滑的曲线。得到的可能是跟鸟巢一样的图像

x1_new=x1.sort_values()

x1_new

已经排序好，重新定义a，b，c和x2_new

a=theta4
b=theta2+theta5*x1_new
c=theta0+theta1*x1_new+theta3*x1_new*x1_new
x2_new=(-b+np.sqrt(b*b-4*a*c))/(2*a)

7、可视化散点图和二阶决策边界函数

fig4=plt.figure()
passed=plt.scatter(data['Exam1'][mask],data['Exam2'][mask])
failed=plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask])
plt.legend((passed,failed),('pass','fail'))
plt.plot(x1_new,x2_new)
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.title('Exam1-Exam2')
plt.show()

可以看到二阶决策边界函数是一条曲线

实战三：芯片质量预测

1、导入数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path='Desktop/artificial_intelligence/Chapter3/chip_test.csv'
data_chip=pd.read_csv(path)
data_chip.head()

2、可视化数据

mask=data_chip['pass']==1
fig=plt.figure()
passed=plt.scatter(data_chip['test1'][mask],data_chip['test2'][mask])
failed=plt.scatter(data_chip['test1'][~mask],data_chip['test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('pass','fail'))
plt.show()

3、生成新的特征数据并赋值

x1=data_chip['test1']
x2=data_chip['test2']
res={'x1':x1,'x2':x2,'x1x1':x1x1,'x2x2':x2x2,'x1x2':x1x2}
X_chip=pd.DataFrame(res)
y=data_chip['pass']
X_chip.head()

4、创建模型并训练

from sklearn.linear_model import LogisticRegression
lr3=LogisticRegression()
lr3.fit(X_chip,y)

5、模型预测

y_pred=lr3.predict(X_chip)

6、评估模型的准确率

from sklearn.metrics import accuracy_score
accu=accuracy_score(y,y_pred)
accu

0.8135593220338984

7、对各个系数的θ赋值

theta0=lr3.intercept_
theta1=lr3.coef_[0][0]
theta2=lr3.coef_[0][1]
theta3=lr3.coef_[0][2]
theta4=lr3.coef_[0][3]
theta5=lr3.coef_[0][4]
print(theta1,'\n',theta2,'\n',theta3,'\n',theta4,'\n',theta5)

0.3501464610494274

0.6713687123833845

-2.7815298580915697

-2.390460834807681

-0.9568611386972838

8、定义函数，求解决策边界函数

根据上个实战求解出的关系方程式，定义个函数

def f(x):
    a=theta4
    b=theta2+theta5*x1
    c=theta0+theta1*x1+theta3*x1*x1
    x2_new_1=(-b+np.sqrt(b*b-4*a*c))/(2*a)
    x2_new_2=(-b-np.sqrt(b*b-4*a*c))/(2*a)
    return x2_new_1,x2_new_2
x1=x1.sort_values()
x2_new_1=f(x1)[0]
x2_new_2=f(x2)[1]

9、描绘决策边界曲线

fig2=plt.figure()
passed=plt.scatter(data_chip['test1'][mask],data_chip['test2'][mask])
failed=plt.scatter(data_chip['test1'][~mask],data_chip['test2'][~mask])
plt.plot(x1,x2_new_1)
plt.plot(x1,x2_new_2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('pass','fail'))
plt.show()

可以看到是没有闭合的曲线，原因是因为x1的取值范围小了，在闭合处附近，没有x1的值，所以才没有闭合，我们可以手动添加点x1的数值。

10、描绘完整的决策边界曲线

从上图中可以看到不是完整的曲线，从图上可以看到我们可以将x1的取值范围扩大到-0.75到1.00

x1_new=np.arange(-0.75,1,0.0001)
x1_new

array([-0.75 , -0.7499, -0.7498, ..., 0.9997, 0.9998, 0.9999])

根据x1_new的数据重新生成x2_new的数据，重新可视化

x2_new_3=f(x1_new)[0]
x2_new_4=f(x1_new)[1]

fig3=plt.figure()
passed=plt.scatter(data_chip['test1'][mask],data_chip['test2'][mask])
failed=plt.scatter(data_chip['test1'][~mask],data_chip['test2'][~mask])
plt.plot(x1_new,x2_new_3)
plt.plot(x1_new,x2_new_4)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('pass','fail'))
plt.show()

可以看到已经描绘出完整的决策边界曲线

总结

1、逻辑回归主要用到sigmoid方程。核心思想是把线性回归的结果映射到sigmoid方程中，然后再根据结果做出判断，大于等于0.5就是正样本1，小于0.5就是负样本0。

所以逻辑回归是解决分类问题的，但是底层逻辑还是用到了回归分析。

2、在低维中可以用可视化散点图和决策边界曲线的图像直观看到模型的好坏，也可以用准确率评估指标，在高维中，做不到可视化图像的情况下，可以用评估指标来评估模型的好坏。

3、在可视化二阶曲线的时候，x1需要先排序，因为不排序的话，样本中的x1是乱的，得到的就不是一条平滑的曲线，一阶的时候没影响，因为是直线，从直线内部的哪个点开始，到直线的哪个点结束，还都是在那条直线上。

4、逻辑回归模型中是否用到的决策边界曲线的阶数越高越好，对于二分类的问题是否还有更好的模型，这些问题后面会再系统的学习更新。

更多详细的内容请观看flare老师的视频：Python3系统入门人工智能-慕课网实战