李沐-动手学深度学习笔记-卷积神经网络
参考GitHub
文章目录
-
- 基本理论
- 卷积层
- 卷积层里的填充和步幅
- 多个输入和输出通道
-
- 做个总结:
- 池化层
-
- 代码实现:
- 和别人的交流
基本理论
概念纠正:
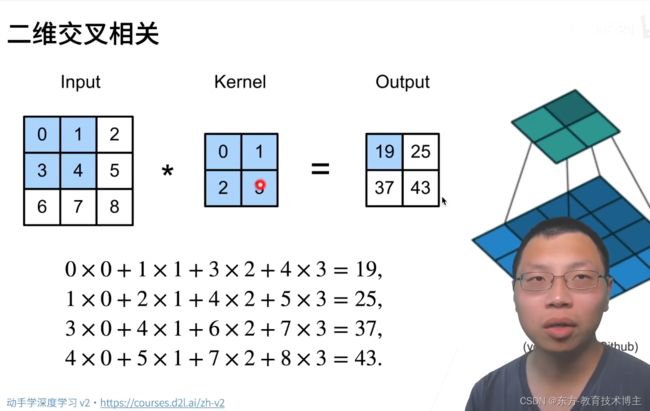
严格来说,卷积是二维交叉相关。(详见更多在沐神评论区)


卷积层

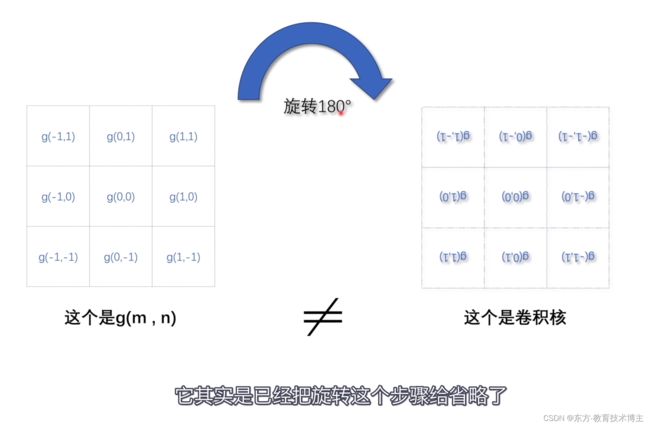
唯一的区别是:卷积多了-号,但是因为对称性会导致没啥区别都一样。


代码:
两层for循环核心就是 :遍历输入 和 卷积核矩阵每个元素相乘再相加。
# 互相关运算
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): # X 为输入,K为核矩阵
"""计算二维互相关信息"""
h, w = K.shape # 核矩阵的行数和列数
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # X.shape[0]为输入高
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum() # 图片的小方块区域与卷积核做点积
return Y
# 验证上述二维互相关运算的输出
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
K = torch.tensor([[0.0,1.0],[2.0,3.0]])
print(corr2d(X,K))
print("ok")
运行结果
tensor([[19., 25.],
[37., 43.]])
ok
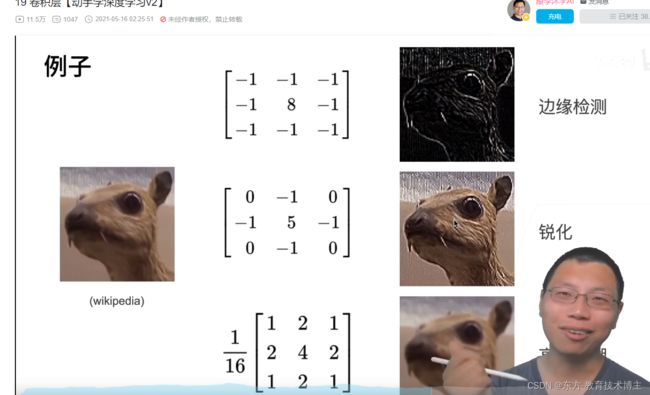
应用:检测边缘
print(corr2d(X, K)) # X.t() 为X的转置,而K卷积核只能检测垂直边缘
代码:
# 互相关运算
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): # X 为输入,K为核矩阵
"""计算二维互相关信息"""
h, w = K.shape # 核矩阵的行数和列数
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # X.shape[0]为输入高
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum() # 图片的小方块区域与卷积核做点积
return Y
# 验证上述二维互相关运算的输出
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
K = torch.tensor([[0.0,1.0],[2.0,3.0]])
print(corr2d(X,K))
print("ok")
# 实现二维卷积层
class Conv2D(nn.Module):
def __init__(self, kernel_size):
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
# 卷积层的一个简单应用:检测图片中不同颜色的边缘
X = torch.ones((6, 8))
X[:, 2:6] = 0 # 把中间四列设置为0
print(X) # 0 与 1 之间进行过渡,表示边缘
K = torch.tensor([[1.0, -1.0]]) # 如果左右原值相等,那么这两原值乘1和-1相加为0,则不是边缘
Y = corr2d(X, K)
print(Y)
print(corr2d(X, K)) # X.t() 为X的转置,而K卷积核只能检测垂直边缘
可以把X换成X.t对比着看效果
这里先后给出x.t(转置)和不转置的结果(源自下面B站 时间 20:43)
tensor([[19., 25.],
[37., 43.]])
ok
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
tensor([[19., 25.],
[37., 43.]])
ok
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
对比可以看到转置全为0,不转置全为1。
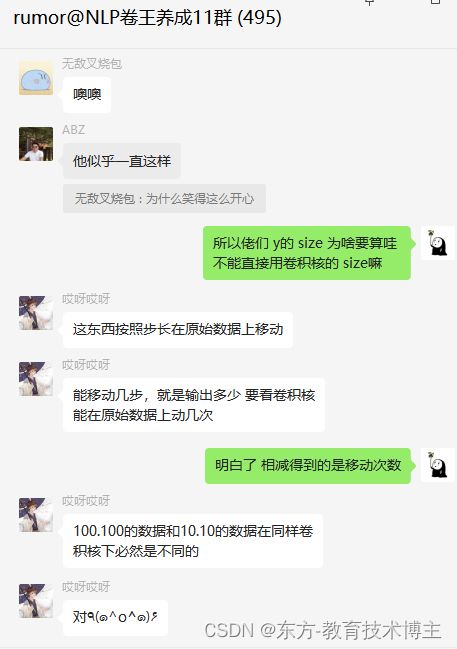
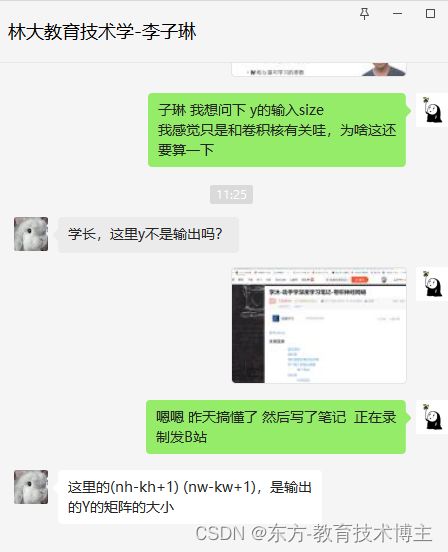
一个问题: 我想问下 y的输入size 我感觉只是和卷积核有关哇,为啥这还要算一下
然后自己在沐神评论区找了卷积视频
【从“卷积”、到“图像卷积操作”、再到“卷积神经网络”,“卷积”意义的3次改变】
卷积可视化网站
这样我看了这个视频
就明白了很多
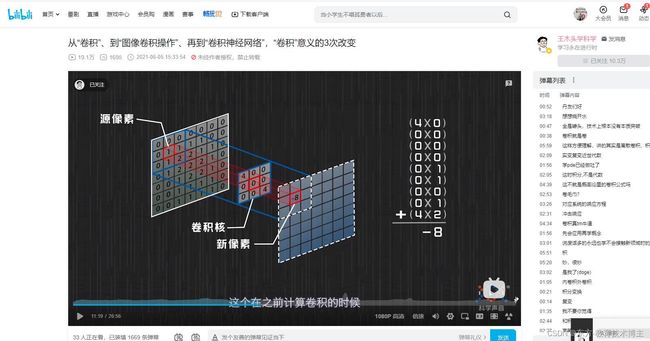
卷积公式

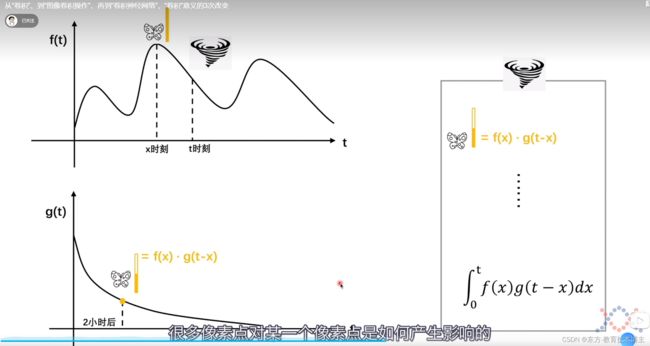
这一步的公式推导在写论文的时候可能用来解释
课堂对话的序列前后之间的影响
比较重要。
上图为平滑卷积操作。
卷积层里的填充和步幅
代码:
补充知识点:
padding=(0,1)padding= (1,0),
会在行的最前和最后都增加一行0。比方说,原来的尺寸为(None,20,11,1),padding之后就会变成(None,22,11,1).
padding=
(1,1),会在行和列的最前和最后都增加一行0。比方说,原来的尺寸为(None,20,11,1),padding之后就会变成(None,22,13,1).
stride=(3,4)
nn.Conv2d
# 在所有侧边填充1个像素
import torch
from torch import nn
def comp_conv2d(conv2d, X): # conv2d 作为传参传进去,在内部使用
X = X.reshape((1,1)+X.shape) # 在维度前面加入一个通道数和批量大小数
Y = conv2d(X) # 卷积处理是一个四维的矩阵
return Y.reshape(Y.shape[2:]) # 将前面两个维度拿掉
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1) # padding=1 为左右都填充一行
X = torch.rand(size=(8,8))
print(comp_conv2d(conv2d,X).shape)
conv2d = nn.Conv2d(1,1,kernel_size=(5,3),padding=(2,1))
print(comp_conv2d(conv2d,X).shape)
# 将高度和宽度的步幅设置为2
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2)
print(comp_conv2d(conv2d,X).shape)
# 一个稍微复杂的例子
conv2d = nn.Conv2d(1,1,kernel_size=(3,5),padding=(0,1),stride=(3,4))
print(comp_conv2d(conv2d,X).shape)
多个输入和输出通道
补充知识点
- 参考一篇评论区笔记
- 科普rgb三通道
- 第一层(最外层)中括号里面包含了两个中括号(以逗号进行分割),这就是(2,3,4)中的2
第二层中括号里面包含了三个中括号(以逗号进行分割),这就是(2,3,4)中的3
第三层中括号里面包含了四个数(以逗号进行分割),这就是(2,3,4)中的4 - 理论知识(国外)
- stack函数
print(torch.stack((T1,T2),dim=0).shape)
print(torch.stack((T1,T2),dim=1).shape)
print(torch.stack((T1,T2),dim=2).shape)
print(torch.stack((T1,T2),dim=3).shape)
# outputs:
torch.Size([2, 3, 3])
torch.Size([3, 2, 3])
torch.Size([3, 3, 2])
'选择的dim>len(outputs),所以报错'
IndexError: Dimension out of range (expected to be in range of [-3, 2], but got 3)
所以说核心就是这个生成的新维度 在三维中处于哪一维度(第0,第1,还是第2)
做个总结:
卷积运算(互相关):是矩阵的点积
多通道输入是点积的基础上求和,
多通道输出:就是把多通道输入的结果在指定维度(0维度)堆叠
代码和运行结果如下
# 多输入通道互相关运算
import torch
from d2l import torch as d2l
from torch import nn
# 多通道输入运算
def corr2d_multi_in(X,K):
#核心在于求和
return sum(d2l.corr2d(x,k) for x,k in zip(X,K)) # X,K为3通道矩阵,for使得对最外面通道进行遍历
X = torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],
[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])
K = torch.tensor([[[0.0,1.0],[2.0,3.0]],[[1.0,2.0],[3.0,4.0]]])
print(X.shape)
print(K.shape)
print(corr2d_multi_in(X,K))
# 多输出通道运算
def corr2d_multi_in_out(X,K): # X为3通道矩阵,K为4通道矩阵,最外面维为输出通道
return torch.stack([corr2d_multi_in(X,k) for k in K],0) # 大k中每个小k是一个3D的Tensor。0表示stack堆叠函数里面在0这个维度堆叠。
print(K.shape)
print((K+1).shape)
print((K+2).shape)
print(K)
print(K+1)
K = torch.stack((K, K+1, K+2),0) # K与K+1之间的区别为K的每个元素加1
print(K.shape)
print(corr2d_multi_in_out(X,K))
结果:
torch.Size([2, 3, 3])
torch.Size([2, 2, 2])
tensor([[ 56., 72.],
[104., 120.]])
torch.Size([2, 2, 2])
torch.Size([2, 2, 2])
torch.Size([2, 2, 2])
tensor([[[0., 1.],
[2., 3.]],
[[1., 2.],
[3., 4.]]])
tensor([[[1., 2.],
[3., 4.]],
[[2., 3.],
[4., 5.]]])
torch.Size([3, 2, 2, 2])
tensor([[[ 56., 72.],
[104., 120.]],
[[ 76., 100.],
[148., 172.]],
[[ 96., 128.],
[192., 224.]]])
池化层

最大池化用来增加容错

平均池化层:可以柔和化
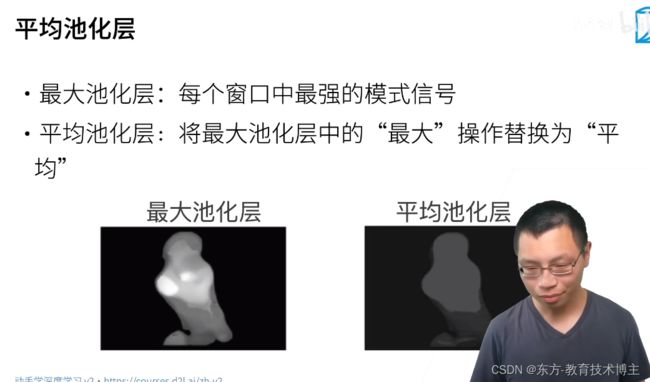

池化的操作类似卷积:
代码实现:
补充:
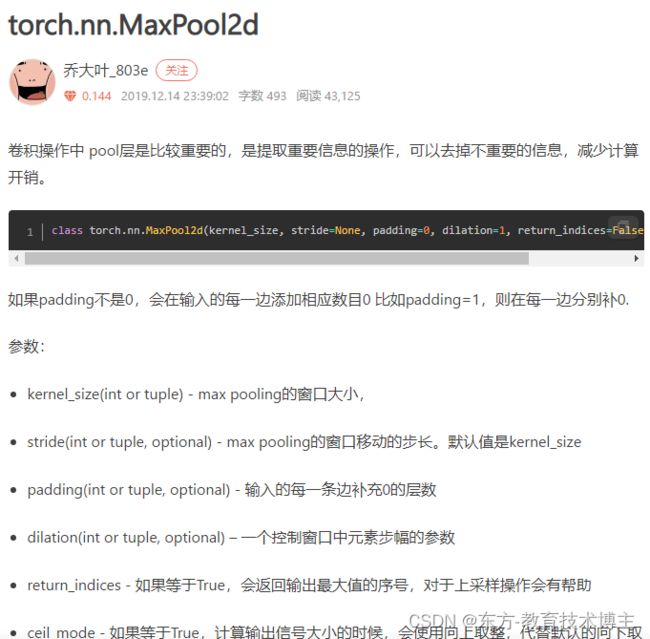
torch.nn.MaxPool2d
C = torch.cat( (A,B),0 ) #按维数0拼接(竖着拼)
C = torch.cat( (A,B),1 ) #按维数1拼接(横着拼)
全部代码:
import torch
from torch import nn
from d2l import torch as d2l
# 实现池化层的正向传播
def pool2d(X, pool_size, mode='max'): # 拿到输入,池化窗口大小
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1)) # 输入的高减去窗口的高,再加上1,这里没有padding
for i in range(Y.shape[0]): # 行遍历
for j in range(Y.shape[1]): # 列遍历
if mode == 'max':
Y[i,j] = X[i:i + p_h, j:j + p_w].max()
elif mode == 'avg':
Y[i,j] = X[i:i + p_h, j:j + p_w].mean()
return Y
# 验证二维最大池化层的输出
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
print(pool2d(X, (2,2)))
# 验证平均池化层
print(pool2d(X, (2,2), 'avg'))
# 填充和步幅
X = torch.arange(16,dtype=torch.float32).reshape((1,1,4,4))
print(X)
pool2d = nn.MaxPool2d(3) # 深度学习框架中的步幅默认与池化窗口的大小相同,下一个窗口和前一个窗口没有重叠的
pool2d(X)
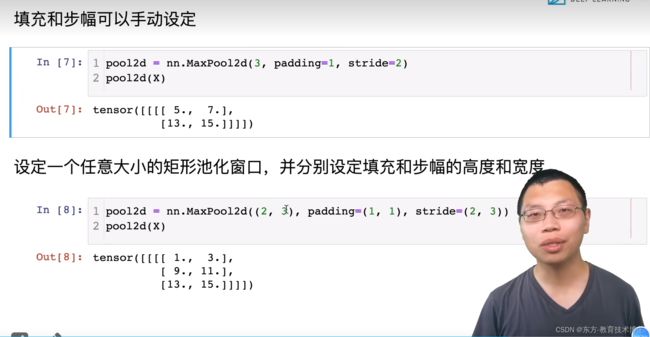
# 填充和步幅可以手动设定
pool2d = nn.MaxPool2d(3,padding=1,stride=2)
print(pool2d(X))
# 设定一个任意大小的矩形池化窗口,并分别设定填充和步幅的高度和宽度
pool2d = nn.MaxPool2d((2,3),padding=(1,1),stride=(2,3))
print(pool2d(X))
# 池化层在每个通道上单独运算
X = torch.cat((X,X+1),1)
print(X.shape) # 合并起来,变成了1X2X4X4的矩阵
print(X)
pool2d = nn.MaxPool2d(3,padding=1,stride=2)
print(pool2d(X))
运行结果:
tensor([[4., 5.],
[7., 8.]])
tensor([[2., 3.],
[5., 6.]])
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]]]])
tensor([[[[ 5., 7.],
[13., 15.]]]])
tensor([[[[ 1., 3.],
[ 9., 11.],
[13., 15.]]]])
torch.Size([1, 2, 4, 4])
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]],
[[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.],
[13., 14., 15., 16.]]]])
tensor([[[[ 5., 7.],
[13., 15.]],
[[ 6., 8.],
[14., 16.]]]])