CRF(条件随机场)
CRF(条件随机场)
- 前言
- 一、马尔可夫随机场
- 二、条件随机场
-
-
- 1、Where CRF?
- 2、随机场->马尔可夫随机场->条件随机场->线性链条件随机场
- 3、线性链条件随机场的参数化形式
- 4、线性链条件随机场实例
-
- reference
前言
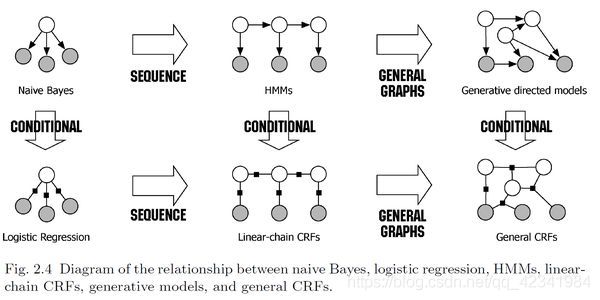
条件随机场是一种判别式无向图模型。
生成式模型是直接对联合分布进行建模,而判别式模型则是对条件分布进行建模。
条件随机场试图对多个变量在给定观测值后的条件概率进行建模,具体来说,若令 x = { x 1 , x 2 , . . . , x n } x = \{x_1,x_2,...,x_n\} x={x1,x2,...,xn}为观测序列, y = { y 1 , y 2 , . . . , y n } y = \{y_1,y_2,...,y_n\} y={y1,y2,...,yn}为与之相应的标记序列,则条件随机场的目标是构建条件概率模型 P ( y ∣ x ) P(y|x) P(y∣x)。
一、马尔可夫随机场
马尔可夫随机场(Markov Random Field,MRF)是典型的马尔可夫网,这是一种无向图模型。图中每个结点表示一个或一组变量,结点之间的边表示两个变量之间的依赖关系。马尔可夫随机场有一组势函数(potential functions),亦称因子(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
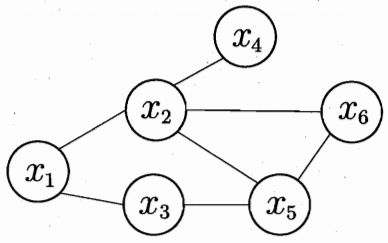
如下图即一个简单的马尔可夫随机场:
在一个马尔可夫随机场中定义如下概念:
- 团(clique):对于图中结点的一个子集,若其中任意两个结点之间都有边连接,则称该子集为一个团;
- 极大团(maximal clique):若某个团加入另外任何一个结点都不能再够成团,则称该团为极大团,即极大团就是不能被其他团所包含的团。
马尔可夫随机场中,所有变量的联合概率可以通过团来定义,每个因子仅与一个团相关。若所有的团构成集合 C C C,与团 Q Q Q相关的变量集合记为 x Q x_Q xQ,则联合概率定义为:
P ( x ) = 1 Z ∏ Q ∈ C ψ Q ( x Q ) , ( 14.2 ) P(x)=\frac{1}{Z}\prod_{Q\in C}^{} \psi _{Q}(x_Q),(14.2) P(x)=Z1Q∈C∏ψQ(xQ),(14.2)其中 ψ Q ψ_Q ψQ为与团 Q Q Q对应的势函数,用于对团 Q Q Q中的变量关系进行建模。
有向图模型是一系列概率的连乘形式,无向图模型则是一系列函数的连乘形式。
二、条件随机场
1、Where CRF?
自然语言处理中的词性标注(POS Tagging)就是非常适合CRF使用的地方。词性标注的目标是给出一个句子中每个词的词性(名词,动词,形容词等)。而这些词的词性往往和上下文的词的词性有关,为了让我们的分类器表现的更好,可以在标记数据的时候,可以考虑相邻数据的标记信息。如:“Bob (名词) drank(动词) coffee(名词) at(介词) Starbucks(名词)”,词性标注序列(名词,动词,名词,介词,名词)显然比(名词,动词,动词,介词,名词)更靠谱。动词后面还是动词显然是说不通的。
2、随机场->马尔可夫随机场->条件随机场->线性链条件随机场
- 随机场:随机场是由若干个位置组成的整体,当给每一个位置中按照某种分布随机赋予一个值之后,其全体就叫做随机场。
- 马尔可夫随机场:马尔科夫随机场是随机场的特例,它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关,和与其不相邻的位置的赋值无关。
- 条件随机场:CRF是马尔科夫随机场的特例,它假设马尔科夫随机场中只有X和Y两种变量,X一般是给定的,而Y一般是在给定X的条件下的输出。这样马尔科夫随机场就特化成了条件随机场。
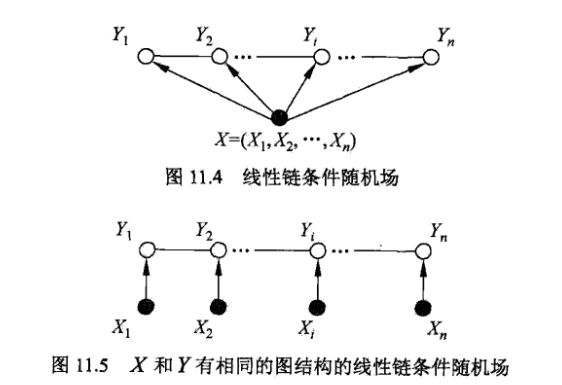
- 线性链条件随机场:X和Y有相同的结构的CRF就构成了线性链条件随机场(Linear chain Conditional Random Fields,以下简称 linear-CRF)。
3、线性链条件随机场的参数化形式
与马尔可夫随机场定义联合概率的方式类似,条件随机场使用势函数和图结构上的团来定义条件概率 P ( y ∣ x ) P(y|x) P(y∣x).给定观测序列 x x x,图14.6所示的链式条件随机场主要包含两种关于标记变量的团,即
- 单个标记变量 { y i } \{y_i\} {yi}
- 相邻的标记变量 { y i − 1 , y i } \{y_{i-1},y_i\} {yi−1,yi}。
选择合适的势函数,即可得到形如式(14.2)的条件概率定义。
在条件随机场中,通过选用指数势函数并引入特征函数(feature function),条件概率被定义为
P ( y ∣ x ) = 1 Z exp ( ∑ j ∑ i = 1 n − 1 λ j t j ( y i + 1 , y i , x , i ) + ∑ k ∑ i = 1 n μ k s k ( y i , x , i ) ) , ( 14.11 ) P(\mathbf{y} \mid \mathbf{x})=\frac{1}{Z} \exp \left(\sum_{j} \sum_{i=1}^{n-1} \lambda_{j} t_{j}\left(y_{i+1}, y_{i}, \mathbf{x}, i\right)+\sum_{k} \sum_{i=1}^{n} \mu_{k} s_{k}\left(y_{i}, \mathbf{x}, i\right)\right),(14.11) P(y∣x)=Z1exp(j∑i=1∑n−1λjtj(yi+1,yi,x,i)+k∑i=1∑nμksk(yi,x,i)),(14.11)
其中,
- t j ( y i + 1 , y i , x , i ) t_{j}\left(y_{i+1}, y_{i}, \mathbf{x}, i\right) tj(yi+1,yi,x,i)是定义在观测序列的两个相邻标记位置上的转移特征函数(transition feature function),用于刻画相邻标记变量之间的相关关系以及观测序列对它们的影响,
- s k ( y i , x , i ) s_{k}\left(y_{i}, \mathbf{x}, i\right) sk(yi,x,i)是定义在观测序列的标记位置i上的状态特征函数(status feature function),用于刻画观测序列对标记变量的影响,
- λ \lambda λ 和 μ k μ_k μk为参数,Z为规范化因子,用于确保式(14.11)是正确定义的概率。
特征函数和权重系数的实际意义是什么?
每个特征函数定义了一个linear-CRF的规则,则其系数定义了这个规则的可信度。所有的规则和其可信度一起构成了我们的linear-CRF的最终的条件概率分布。
4、线性链条件随机场实例
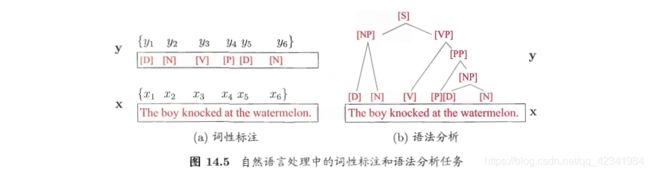
显然,要使用条件随机场,还需定义合适的特征函数,特征函数通常是实值函数,以刻画数据的一些很可能成立或期望成立的经验特性。以图14.5(a)的词性标注任务为例,若采用转移特征函数
t j ( y i + 1 , y i , x , i ) = { 1 , if y i + 1 = [ P ] , y i = [ V ] and x i = “ k n o c k ” 0 , otherwise t_{j}\left(y_{i+1}, y_{i}, \mathbf{x}, i\right)=\left\{\begin{array}{ll} 1, & \text { if } y_{i+1}=[P], y_{i}=[V] \text { and } x_{i}=“\mathrm{knock}” \\ 0, & \text { otherwise } \end{array}\right. tj(yi+1,yi,x,i)={1,0, if yi+1=[P],yi=[V] and xi=“knock” otherwise
则表示第 i i i个观测值 x i x_i xi为单词“knock”时,相应的标记 y i y_i yi和 y i + 1 y_{i+1} yi+1很可能分别为 [ V ] [V] [V]和 [ P ] [P] [P]。若采用状态特征函数
s k ( y i , x , i ) = { 1 , if y i = [ V ] and x i = “ k n o c k ” 0 , otherwise s_{k}\left(y_{i}, \mathbf{x}, i\right)=\left\{\begin{array}{ll} 1, & \text { if } y_{i}=[V] \text { and } x_{i}=“\mathrm{knock}” \\ 0, & \text { otherwise } \end{array}\right. sk(yi,x,i)={1,0, if yi=[V] and xi=“knock” otherwise
则表示观测值 x i x_i xi为单词“knock”时,它所对应的标记很可能为 [ V ] [V] [V]。
对比式(11)和(2)可看出,条件随机场和马尔可夫随机场均使用团上的势函数定义概率,两者在形式上没有显著区别;但条件随机场处理的是条件概率,而马尔可夫随机场处理的是联合概率。
reference
[1]周志华-《机器学习》
[2]李航-《统计学习方法》
[3]【归纳综述】马尔可夫、隐马尔可夫 HMM 、条件随机场 CRF 全解析及其python实现