机器学习-决策树之回归树
一、决策树之回归树- DecisionTreeRegressor
1.参数
sklearn.tree.DecisionTreeRegressor (criterion=’mse’, splitter=’best’, max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None,random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)
几乎所有参数,属性及接口都和分类树一模一样。需要注意的是,在回归树种,没有标签分布是否均衡的问题,因此没有class_weight这样的参数。
1.13.1 重要参数,属性及接口
criterion
回归树衡量分枝质量的指标,支持的标准有三种:
1)输入"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失
2)输入“friedman_mse”使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
3)输入"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失
属性中最重要的依然是feature_importances_,接口依然是apply, fit, predict, score最核心。

其中N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi是样本点i实际的数值标签。所以MSE的本质,其实是样本真实数据与回归结果的差异。在回归树中,MSE不只是我们的分枝质量衡量指标,也是我们最常用的衡量回归树回归质量的指标,当我们在使用交叉验证,或者其他方式获取回归树的结果时,我们往往选择均方误差作为我们的评估(在分类树中这个指标是score代表的预测准确率)。在回归中,我们追求的是,MSE越小越好。
然而,回归树的接口score返回的是R平方,并不是MSE。R平方被定义如下:

其中u是残差平方和(MSE * N),v是总平方和,N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi是样本点i实际的数值标签。y帽是真实数值标签的平均数。R平方可以为正为负(如果模型的残差平方和远远大于模型的总平方和,模型非常糟糕,R平方就会为负),而均方误差永远为正。
**值得一提的是,虽然均方误差永远为正,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误差“(neg_mean_squared_error)。**这是因为sklearn在计算模型评估指标的时候,会考虑指标本身的性质,均方误差本身是一种误差,所以被sklearn划分为模型的一种损失(loss),因此在sklearn当中,都以负数表示。真正的均方误差MSE的数值,其实就是neg_mean_squared_error去掉负号的数字。
1.2下面给出回归树的基本步骤
#1.导入数据集和包
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
#实例化
regressor = DecisionTreeRegressor(random_state=0)
#交叉验证(或者用测试集或者是训练集也是可以的)
cross_val_score(regressor, boston.data, boston.target, cv=10,
scoring = "neg_mean_squared_error")
#交叉验证cross_val_score的用法自己在去摸索
二、下面给出一个比较简单的实例-一元回归图像实例
接下来我们到二维平面上来观察决策树是怎样拟合一条曲线的。我们用回归树来拟合正弦曲线,并添加一些噪声来观察回归树的表现。
2.1导入相关库
#1.导入需要的库
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
2.2导入数据(创建数据)
# 2.创建一条噪声正弦函数
'''在这一步,我们的基本思路是,先创建一组随机的,分布在0~5上的横坐标轴的取值(x),然后将这一组值放到sin函 数中去生成纵坐标的值(y),接着再到y上去添加噪声。全程我们会使用numpy库来为我们生成这个正弦曲线。'''
rng=np.random.RandomState(1)#生成随机数种子
x=np.sort(5*rng.rand(80,1),axis=0)#将随机生成的二维数组,并进行排序
y=np.sin(x).ravel()#注意在画图的时候,需要是1维的,就需要ravel()一下
#为了降维用ravel()
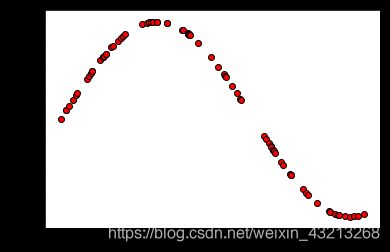
fig=plt.figure(figsize=(6,4))
plt.scatter(x,y,c='r',edgecolors='black')
plt.show()
'''#了解降维函数ravel()的用法
np.random.random((2,1))
np.random.random((2,1)).ravel()
np.random.random((2,1)).ravel().shape'''
多次运行可以不断进行降维
y[::5]+=3*(0.5-rng.rand(16))#表示间隔为5 的16个数加都加上一个随机数
# (就是加上噪声)
plt.scatter(x,y,c='r',edgecolors='black')
plt.show()
2.4开始正式建模了-实例化和训练模型
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(x, y)
regr_2.fit(x, y)
#训练两个模型(用于对比)
2.5训练集导入模型预测结果
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
#np.arrange(开始点,结束点,步长) 生成有序数组的函数
'''#了解增维切片np.newaxis的用法
l = np.array([1,2,3,4])
l
l.shape
l[:,np.newaxis]
l[:,np.newaxis].shape
l[np.newaxis,:].shape
'''
2.6可视化展示
#开始画图
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black",c="darkorange", label="data")
plt.plot(x_test, y_1, color="cornflowerblue",label="max_depth=2", linewidth=2)
plt.plot(x_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
结果如下所示

**分析结果:**可见,回归树学习了近似正弦曲线的局部线性回归。我们可以看到,如果树的最大深度(由max_depth参数控制)设置得太高,则决策树学习得太精细,它从训练数据中学了很多细节,包括噪声得呈现,从而使模型偏离真实的正弦曲线,形成过拟合。