MXNet-图像分类(symbol版本)【附源码】
文章目录
- 前言
- 图像的发展史及意义
- 一、图像分类模型构建
-
- 0.MLP的实现(1986-1989年)
- 1.LeNet的实现(1994年)
- 2.AlexNet的实现(2012年)
- 3.VGG的实现(2014年)
- 4.GoogleNet的实现(2014年)
- 5.ResNet的实现(2015年)
- 6.MobileNet_V1的实现(2017年)
- 7.MobileNet_V2的实现(2019年)
- 8.ResNext的实现(2016年)
- 9.inception_V4的实现(2016年)
- 二、数据集的准备
-
- 1.数据集描述
- 2.数据集准备
- 三、模型训练
-
- 1.数据加载器
- 2.mxnet模型初始化
- 3.学习率的设置
- 4.断点设置
- 5.模型训练
- 四、模型预测
- 五、模型主入口
- 总结
前言
本文基于mxnet的symbol实现图像分类,本文基于多个网络结构实现图像分类
图像的发展史及意义
在神经网络和深度学习领域,Yann LeCun可以说是元老级人物。他于1998年在 IEEE 上发表了一篇42页的长文,文中首次提出卷积-池化-全连接的神经网络结构,由LeCun提出的七层网络命名LeNet5,因而也为他赢得了卷积神经网络之父的美誉。CNN在近几年的发展历程中,从经典的LeNet5网络到最近号称最好的图像分类网络EfficientNet,大量学者不断的做出了努力和创新。
在后面的一些图像算法过程中,图像分类的网络结构起到了举足轻重的作用,他们都依赖于分类网络做主干特征提取网络,有一定的程度体现出特征提取能力。
一、图像分类模型构建
本文基于mxnet实现图像分类的网络结构,下边对各个网络结构进行介绍,后续只需要稍作修改即可完成网络结构的替换
0.MLP的实现(1986-1989年)
论文地址:https://ieeexplore.ieee.org/document/9747172
网络结构:

MLP(Multi-Layer Perceptron),即多层感知器,是一种趋向结构的人工神经网络,映射一组输入向量到一组输出向量。MLP可以被看做是一个有向图,由多个节点层组成,每一层全连接到下一层。除了输入节点,每个节点都是一个带有非线性激活函数的神经元(或称处理单元)。一种被称为反向传播算法的监督学习方法常被用来训练MLP。MLP是感知器的推广,克服了感知器无法实现对线性不可分数据识别的缺点。
代码实现:
def get_symbol(num_classes=10):
data = mx.symbol.Variable('data')
data = mx.sym.Flatten(data=data)
fc1 = mx.symbol.FullyConnected(data = data, name='fc1', num_hidden=128)
act1 = mx.symbol.Activation(data = fc1, name='relu1', act_type="relu")
fc2 = mx.symbol.FullyConnected(data = act1, name = 'fc2', num_hidden = 64)
act2 = mx.symbol.Activation(data = fc2, name='relu2', act_type="relu")
fc3 = mx.symbol.FullyConnected(data = act2, name='fc3', num_hidden=num_classes)
mlp = mx.symbol.SoftmaxOutput(data = fc3, name = 'softmax')
return mlp
1.LeNet的实现(1994年)
论文地址:https://ieeexplore.ieee.org/document/726791
网络结构:
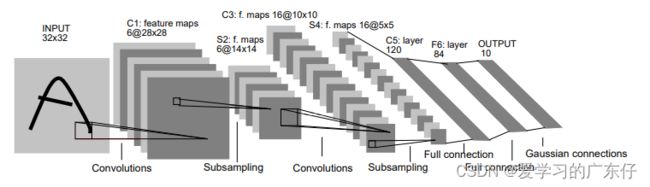
LeNet由Yann Lecun 提出,是一种经典的卷积神经网络,是现代卷积神经网络的起源之一。Yann将该网络用于邮局的邮政的邮政编码识别,有着良好的学习和识别能力。LeNet又称LeNet-5,具有一个输入层,两个卷积层,两个池化层,3个全连接层(其中最后一个全连接层为输出层)。
LeNet-5是一种经典的卷积神经网络结构,于1998年投入实际使用中。该网络最早应用于手写体字符识别应用中。普遍认为,卷积神经网络的出现开始于LeCun 等提出的LeNet 网络,可以说LeCun 等是CNN 的缔造者,而LeNet-5 则是LeCun 等创造的CNN 经典之作。
LeNet5 一共由7 层组成,分别是C1、C3、C5 卷积层,S2、S4 降采样层(降采样层又称池化层),F6 为一个全连接层,输出是一个高斯连接层,该层使用softmax 函数对输出图像进行分类。为了对应模型输入结构,将MNIST 中的28* 28 的图像扩展为32* 32 像素大小。下面对每一层进行详细介绍。C1 卷积层由6 个大小为5* 5 的不同类型的卷积核组成,卷积核的步长为1,没有零填充,卷积后得到6 个28* 28 像素大小的特征图;S2 为最大池化层,池化区域大小为2* 2,步长为2,经过S2 池化后得到6 个14* 14 像素大小的特征图;C3 卷积层由16 个大小为5* 5 的不同卷积核组成,卷积核的步长为1,没有零填充,卷积后得到16 个10* 10 像素大小的特征图;S4 最大池化层,池化区域大小为2* 2,步长为2,经过S2 池化后得到16 个5* 5 像素大小的特征图;C5 卷积层由120 个大小为5* 5 的不同卷积核组成,卷积核的步长为1,没有零填充,卷积后得到120 个1* 1 像素大小的特征图;将120 个1* 1 像素大小的特征图拼接起来作为F6 的输入,F6 为一个由84 个神经元组成的全连接隐藏层,激活函数使用sigmoid 函数;最后一层输出层是一个由10 个神经元组成的softmax 高斯连接层,可以用来做分类任务。
代码实现(symbol):
def get_loc(data, attr={'lr_mult':'0.01'}):
loc = mx.symbol.Convolution(data=data, num_filter=30, kernel=(5, 5), stride=(2,2))
loc = mx.symbol.Activation(data = loc, act_type='relu')
loc = mx.symbol.Pooling(data=loc, kernel=(2, 2), stride=(2, 2), pool_type='max')
loc = mx.symbol.Convolution(data=loc, num_filter=60, kernel=(3, 3), stride=(1,1), pad=(1, 1))
loc = mx.symbol.Activation(data = loc, act_type='relu')
loc = mx.symbol.Pooling(data=loc, global_pool=True, kernel=(2, 2), pool_type='avg')
loc = mx.symbol.Flatten(data=loc)
loc = mx.symbol.FullyConnected(data=loc, num_hidden=6, name="stn_loc", attr=attr)
return loc
def get_symbol(num_classes=10, add_stn=False, **kwargs):
data = mx.symbol.Variable('data')
if add_stn:
data = mx.sym.SpatialTransformer(data=data, loc=get_loc(data), target_shape = (28,28), transform_type="affine", sampler_type="bilinear")
# first conv
conv1 = mx.symbol.Convolution(data=data, kernel=(5,5), num_filter=20)
tanh1 = mx.symbol.Activation(data=conv1, act_type="tanh")
pool1 = mx.symbol.Pooling(data=tanh1, pool_type="max", kernel=(2,2), stride=(2,2))
# second conv
conv2 = mx.symbol.Convolution(data=pool1, kernel=(5,5), num_filter=50)
tanh2 = mx.symbol.Activation(data=conv2, act_type="tanh")
pool2 = mx.symbol.Pooling(data=tanh2, pool_type="max", kernel=(2,2), stride=(2,2))
# first fullc
flatten = mx.symbol.Flatten(data=pool2)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
tanh3 = mx.symbol.Activation(data=fc1, act_type="tanh")
# second fullc
fc2 = mx.symbol.FullyConnected(data=tanh3, num_hidden=num_classes)
# loss
lenet = mx.symbol.SoftmaxOutput(data=fc2, name='softmax')
return lenet
2.AlexNet的实现(2012年)
论文地址:https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf
网络结构:

AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的。也是在那年之后,更多的更深的神经网络被提出,比如优秀的vgg,GoogLeNet。 这对于传统的机器学习分类算法而言,已经相当的出色。
AlexNet中包含了几个比较新的技术点,也首次在CNN中成功应用了ReLU、Dropout和LRN等Trick。同时AlexNet也使用了GPU进行运算加速。
AlexNet将LeNet的思想发扬光大,把CNN的基本原理应用到了很深很宽的网络中。AlexNet主要使用到的新技术点如下:
- 成功使用ReLU作为CNN的激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题。虽然ReLU激活函数在很久之前就被提出了,但是直到AlexNet的出现才将其发扬光大。
- 训练时使用Dropout随机忽略一部分神经元,以避免模型过拟合。Dropout虽有单独的论文论述,但是AlexNet将其实用化,通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。
- 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖,提升了特征的丰富性。
- 提出了LRN层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
- 使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算。AlexNet使用了两块GTX 580 GPU进行训练,单个GTX 580只有3GB显存,这限制了可训练的网络的最大规模。因此作者将AlexNet分布在两个GPU上,在每个GPU的显存中储存一半的神经元的参数。因为GPU之间通信方便,可以互相访问显存,而不需要通过主机内存,所以同时使用多块GPU也是非常高效的。同时,AlexNet的设计让GPU之间的通信只在网络的某些层进行,控制了通信的性能损耗。
- 数据增强,随机地从256256的原始图像中截取224224大小的区域(以及水平翻转的镜像),相当于增加了2*(256-224)^2=2048倍的数据量。如果没有数据增强,仅靠原始的数据量,参数众多的CNN会陷入过拟合中,使用了数据增强后可以大大减轻过拟合,提升泛化能力。进行预测时,则是取图片的四个角加中间共5个位置,并进行左右翻转,一共获得10张图片,对他们进行预测并对10次结果求均值。同时,AlexNet论文中提到了会对图像的RGB数据进行PCA处理,并对主成分做一个标准差为0.1的高斯扰动,增加一些噪声,这个Trick可以让错误率再下降1%。
代码实现(symbol):
def get_symbol(num_classes, dtype='float32'):
input_data = mx.sym.Variable(name="data")
if dtype == 'float16':
input_data = mx.sym.Cast(data=input_data, dtype=np.float16)
# stage 1
conv1 = mx.sym.Convolution(name='conv1',
data=input_data, kernel=(11, 11), stride=(4, 4), num_filter=96)
relu1 = mx.sym.Activation(data=conv1, act_type="relu")
lrn1 = mx.sym.LRN(data=relu1, alpha=0.0001, beta=0.75, knorm=2, nsize=5)
pool1 = mx.sym.Pooling(
data=lrn1, pool_type="max", kernel=(3, 3), stride=(2,2))
# stage 2
conv2 = mx.sym.Convolution(name='conv2',
data=pool1, kernel=(5, 5), pad=(2, 2), num_filter=256)
relu2 = mx.sym.Activation(data=conv2, act_type="relu")
lrn2 = mx.sym.LRN(data=relu2, alpha=0.0001, beta=0.75, knorm=2, nsize=5)
pool2 = mx.sym.Pooling(data=lrn2, kernel=(3, 3), stride=(2, 2), pool_type="max")
# stage 3
conv3 = mx.sym.Convolution(name='conv3',
data=pool2, kernel=(3, 3), pad=(1, 1), num_filter=384)
relu3 = mx.sym.Activation(data=conv3, act_type="relu")
conv4 = mx.sym.Convolution(name='conv4',
data=relu3, kernel=(3, 3), pad=(1, 1), num_filter=384)
relu4 = mx.sym.Activation(data=conv4, act_type="relu")
conv5 = mx.sym.Convolution(name='conv5',
data=relu4, kernel=(3, 3), pad=(1, 1), num_filter=256)
relu5 = mx.sym.Activation(data=conv5, act_type="relu")
pool3 = mx.sym.Pooling(data=relu5, kernel=(3, 3), stride=(2, 2), pool_type="max")
# stage 4
flatten = mx.sym.Flatten(data=pool3)
fc1 = mx.sym.FullyConnected(name='fc1', data=flatten, num_hidden=4096)
relu6 = mx.sym.Activation(data=fc1, act_type="relu")
dropout1 = mx.sym.Dropout(data=relu6, p=0.5)
# stage 5
fc2 = mx.sym.FullyConnected(name='fc2', data=dropout1, num_hidden=4096)
relu7 = mx.sym.Activation(data=fc2, act_type="relu")
dropout2 = mx.sym.Dropout(data=relu7, p=0.5)
# stage 6
fc3 = mx.sym.FullyConnected(name='fc3', data=dropout2, num_hidden=num_classes)
if dtype == 'float16':
fc3 = mx.sym.Cast(data=fc3, dtype=np.float32)
softmax = mx.sym.SoftmaxOutput(data=fc3, name='softmax')
return softmax
3.VGG的实现(2014年)
论文地址:https://arxiv.org/pdf/1409.1556.pdf
网络结构:
![]()
![]()
VGG模型是2014年ILSVRC竞赛的第二名,第一名是GoogLeNet。但是VGG模型在多个迁移学习任务中的表现要优于googLeNet。而且,从图像中提取CNN特征,VGG模型是首选算法。它的缺点在于,参数量有140M之多,需要更大的存储空间。但是这个模型很有研究价值。
模型的名称——“VGG”代表了牛津大学的Oxford Visual Geometry Group,该小组隶属于1985年成立的Robotics Research Group,该Group研究范围包括了机器学习到移动机器人。下面是一段来自网络对同年GoogLeNet和VGG的描述:
VGG的特点:
- 小卷积核。作者将卷积核全部替换为3x3(极少用了1x1);
- 小池化核。相比AlexNet的3x3的池化核,VGG全部为2x2的池化核;
- 层数更深特征图更宽。基于前两点外,由于卷积核专注于扩大通道数、池化专注于缩小宽和高,使得模型架构上更深更宽的同时,计算量的增加放缓;
- 全连接转卷积。网络测试阶段将训练阶段的三个全连接替换为三个卷积,测试重用训练时的参数,使得测试得到的全卷积网络因为没有全连接的限制,因而可以接收任意宽或高为的输入。
代码实现(symbol):
def get_feature(internel_layer, layers, filters, batch_norm = False):
for i, num in enumerate(layers):
for j in range(num):
internel_layer = mx.sym.Convolution(data = internel_layer, kernel=(3, 3), pad=(1, 1), num_filter=filters[i], name="conv%s_%s" %(i + 1, j + 1))
if batch_norm:
internel_layer = mx.symbol.BatchNorm(data=internel_layer, name="bn%s_%s" %(i + 1, j + 1))
internel_layer = mx.sym.Activation(data=internel_layer, act_type="relu", name="relu%s_%s" %(i + 1, j + 1))
internel_layer = mx.sym.Pooling(data=internel_layer, pool_type="max", kernel=(2, 2), stride=(2,2), name="pool%s" %(i + 1))
return internel_layer
def get_classifier(input_data, num_classes):
flatten = mx.sym.Flatten(data=input_data, name="flatten")
fc6 = mx.sym.FullyConnected(data=flatten, num_hidden=4096, name="fc6")
relu6 = mx.sym.Activation(data=fc6, act_type="relu", name="relu6")
drop6 = mx.sym.Dropout(data=relu6, p=0.5, name="drop6")
fc7 = mx.sym.FullyConnected(data=drop6, num_hidden=4096, name="fc7")
relu7 = mx.sym.Activation(data=fc7, act_type="relu", name="relu7")
drop7 = mx.sym.Dropout(data=relu7, p=0.5, name="drop7")
fc8 = mx.sym.FullyConnected(data=drop7, num_hidden=num_classes, name="fc8")
return fc8
def get_symbol(num_classes, num_layers=16, batch_norm=False, dtype='float32'):
vgg_spec = {11: ([1, 1, 2, 2, 2], [64, 128, 256, 512, 512]),
13: ([2, 2, 2, 2, 2], [64, 128, 256, 512, 512]),
16: ([2, 2, 3, 3, 3], [64, 128, 256, 512, 512]),
19: ([2, 2, 4, 4, 4], [64, 128, 256, 512, 512])}
if num_layers not in vgg_spec:
raise ValueError("Invalide num_layers {}. Possible choices are 11,13,16,19.".format(num_layers))
layers, filters = vgg_spec[num_layers]
data = mx.sym.Variable(name="data")
if dtype == 'float16':
data = mx.sym.Cast(data=data, dtype=np.float16)
feature = get_feature(data, layers, filters, batch_norm)
classifier = get_classifier(feature, num_classes)
if dtype == 'float16':
classifier = mx.sym.Cast(data=classifier, dtype=np.float32)
symbol = mx.sym.SoftmaxOutput(data=classifier, name='softmax')
return symbol
4.GoogleNet的实现(2014年)
论文地址:https://arxiv.org/pdf/1409.4842.pdf
网络结构:
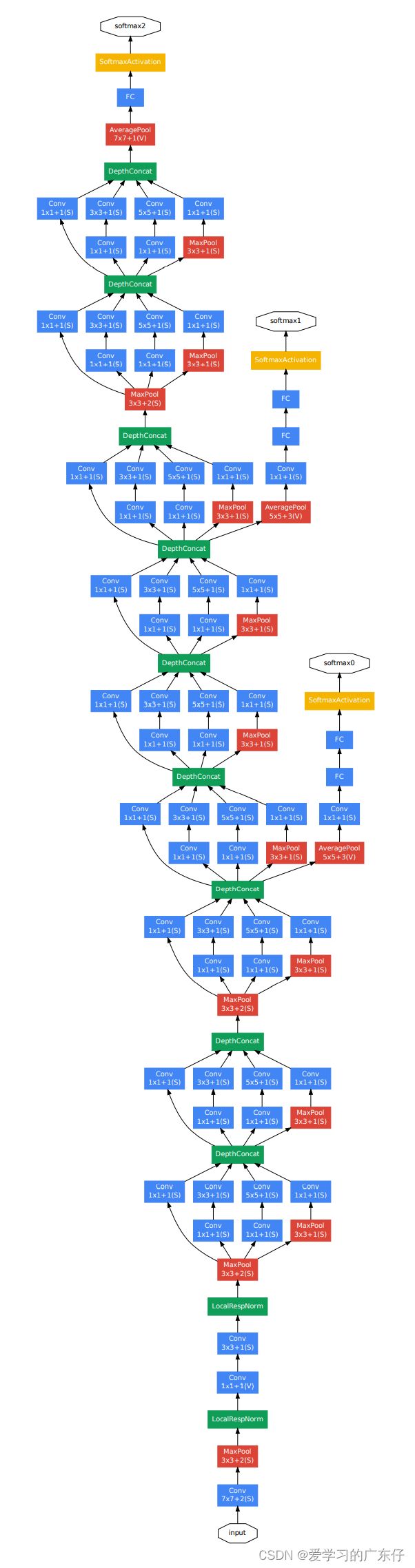
GoogLeNet是2014年Christian Szegedy提出的一种全新的深度学习结构,在这之前的AlexNet、VGG等结构都是通过增大网络的深度(层数)来获得更好的训练效果,但层数的增加会带来很多负作用,比如overfit、梯度消失、梯度爆炸等。inception的提出则从另一种角度来提升训练结果:能更高效的利用计算资源,在相同的计算量下能提取到更多的特征,从而提升训练结果。
inception模块的基本机构如图1,整个inception结构就是由多个这样的inception模块串联起来的。inception结构的主要贡献有两个:一是使用1x1的卷积来进行升降维;二是在多个尺寸上同时进行卷积再聚合。
1x1卷积
作用1:在相同尺寸的感受野中叠加更多的卷积,能提取到更丰富的特征。这个观点来自于Network in Network,图1里三个1x1卷积都起到了该作用。

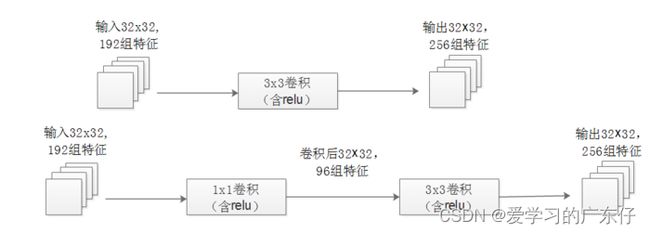
图2左侧是是传统的卷积层结构(线性卷积),在一个尺度上只有一次卷积;图2右图是Network in Network结构(NIN结构),先进行一次普通的卷积(比如3x3),紧跟再进行一次1x1的卷积,对于某个像素点来说1x1卷积等效于该像素点在所有特征上进行一次全连接的计算,所以图2右侧图的1x1卷积画成了全连接层的形式,需要注意的是NIN结构中无论是第一个3x3卷积还是新增的1x1卷积,后面都紧跟着激活函数(比如relu)。将两个卷积串联,就能组合出更多的非线性特征。举个例子,假设第1个3x3卷积+激活函数近似于f1(x)=ax2+bx+c,第二个1x1卷积+激活函数近似于f2(x)=mx2+nx+q,那f1(x)和f2(f1(x))比哪个非线性更强,更能模拟非线性的特征?答案是显而易见的。NIN的结构和传统的神经网络中多层的结构有些类似,后者的多层是跨越了不同尺寸的感受野(通过层与层中间加pool层),从而在更高尺度上提取出特征;NIN结构是在同一个尺度上的多层(中间没有pool层),从而在相同的感受野范围能提取更强的非线性。
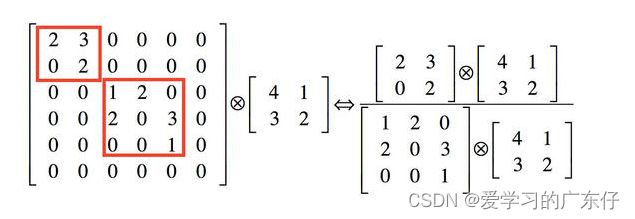
作用2:使用1x1卷积进行降维,降低了计算复杂度。图2中间3x3卷积和5x5卷积前的1x1卷积都起到了这个作用。当某个卷积层输入的特征数较多,对这个输入进行卷积运算将产生巨大的计算量;如果对输入先进行降维,减少特征数后再做卷积计算量就会显著减少。图3是优化前后两种方案的乘法次数比较,同样是输入一组有192个特征、32x32大小,输出256组特征的数据,图3第一张图直接用3x3卷积实现,需要192x256x3x3x32x32=452984832次乘法;图3第二张图先用1x1的卷积降到96个特征,再用3x3卷积恢复出256组特征,需要192x96x1x1x32x32+96x256x3x3x32x32=245366784次乘法,使用1x1卷积降维的方法节省了一半的计算量。有人会问,用1x1卷积降到96个特征后特征数不就减少了么,会影响最后训练的效果么?答案是否定的,只要最后输出的特征数不变(256组),中间的降维类似于压缩的效果,并不影响最终训练的结果。
多个尺寸上进行卷积再聚合
图2可以看到对输入做了4个分支,分别用不同尺寸的filter进行卷积或池化,最后再在特征维度上拼接到一起。这种全新的结构有什么好处呢?Szegedy从多个角度进行了解释:
解释1:在直观感觉上在多个尺度上同时进行卷积,能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。
解释2:利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子图4左侧是个稀疏矩阵(很多元素都为0,不均匀分布在矩阵中),和一个2x2的矩阵进行卷积,需要对稀疏矩阵中的每一个元素进行计算;如果像图4右图那样把稀疏矩阵分解成2个子密集矩阵,再和2x2矩阵进行卷积,稀疏矩阵中0较多的区域就可以不用计算,计算量就大大降低。这个原理应用到inception上就是要在特征维度上进行分解!传统的卷积层的输入数据只和一种尺度(比如3x3)的卷积核进行卷积,输出固定维度(比如256个特征)的数据,所有256个输出特征基本上是均匀分布在3x3尺度范围上,这可以理解成输出了一个稀疏分布的特征集;而inception模块在多个尺度上提取特征(比如1x1,3x3,5x5),输出的256个特征就不再是均匀分布,而是相关性强的特征聚集在一起(比如1x1的的96个特征聚集在一起,3x3的96个特征聚集在一起,5x5的64个特征聚集在一起),这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起,不相关的非关键特征就被弱化,同样是输出256个特征,inception方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入,自然收敛的速度更快。
解释3:Hebbin赫布原理。Hebbin原理是神经科学上的一个理论,解释了在学习的过程中脑中的神经元所发生的变化,用一句话概括就是fire togethter, wire together。赫布认为“两个神经元或者神经元系统,如果总是同时兴奋,就会形成一种‘组合’,其中一个神经元的兴奋会促进另一个的兴奋”。比如狗看到肉会流口水,反复刺激后,脑中识别肉的神经元会和掌管唾液分泌的神经元会相互促进,“缠绕”在一起,以后再看到肉就会更快流出口水。用在inception结构中就是要把相关性强的特征汇聚到一起。这有点类似上面的解释2,把1x1,3x3,5x5的特征分开。因为训练收敛的最终目的就是要提取出独立的特征,所以预先把相关性强的特征汇聚,就能起到加速收敛的作用。
在inception模块中有一个分支使用了max pooling,作者认为pooling也能起到提取特征的作用,所以也加入模块中。注意这个pooling的stride=1,pooling后没有减少数据的尺寸。
代码实现(symbol):
def ConvFactory(data, num_filter, kernel, stride=(1,1), pad=(0, 0), name=None, suffix=''):
conv = mx.symbol.Convolution(data=data, num_filter=num_filter, kernel=kernel, stride=stride, pad=pad, name='conv_%s%s' %(name, suffix))
act = mx.symbol.Activation(data=conv, act_type='relu', name='relu_%s%s' %(name, suffix))
return act
def InceptionFactory(data, num_1x1, num_3x3red, num_3x3, num_d5x5red, num_d5x5, pool, proj, name):
# 1x1
c1x1 = ConvFactory(data=data, num_filter=num_1x1, kernel=(1, 1), name=('%s_1x1' % name))
# 3x3 reduce + 3x3
c3x3r = ConvFactory(data=data, num_filter=num_3x3red, kernel=(1, 1), name=('%s_3x3' % name), suffix='_reduce')
c3x3 = ConvFactory(data=c3x3r, num_filter=num_3x3, kernel=(3, 3), pad=(1, 1), name=('%s_3x3' % name))
# double 3x3 reduce + double 3x3
cd5x5r = ConvFactory(data=data, num_filter=num_d5x5red, kernel=(1, 1), name=('%s_5x5' % name), suffix='_reduce')
cd5x5 = ConvFactory(data=cd5x5r, num_filter=num_d5x5, kernel=(5, 5), pad=(2, 2), name=('%s_5x5' % name))
# pool + proj
pooling = mx.symbol.Pooling(data=data, kernel=(3, 3), stride=(1, 1), pad=(1, 1), pool_type=pool, name=('%s_pool_%s_pool' % (pool, name)))
cproj = ConvFactory(data=pooling, num_filter=proj, kernel=(1, 1), name=('%s_proj' % name))
# concat
concat = mx.symbol.Concat(*[c1x1, c3x3, cd5x5, cproj], name='ch_concat_%s_chconcat' % name)
return concat
def get_symbol(num_classes = 1000):
data = mx.sym.Variable("data")
conv1 = ConvFactory(data, 64, kernel=(7, 7), stride=(2,2), pad=(3, 3), name="conv1")
pool1 = mx.sym.Pooling(conv1, kernel=(3, 3), stride=(2, 2), pool_type="max")
conv2 = ConvFactory(pool1, 64, kernel=(1, 1), stride=(1,1), name="conv2")
conv3 = ConvFactory(conv2, 192, kernel=(3, 3), stride=(1, 1), pad=(1,1), name="conv3")
pool3 = mx.sym.Pooling(conv3, kernel=(3, 3), stride=(2, 2), pool_type="max")
in3a = InceptionFactory(pool3, 64, 96, 128, 16, 32, "max", 32, name="in3a")
in3b = InceptionFactory(in3a, 128, 128, 192, 32, 96, "max", 64, name="in3b")
pool4 = mx.sym.Pooling(in3b, kernel=(3, 3), stride=(2, 2), pool_type="max")
in4a = InceptionFactory(pool4, 192, 96, 208, 16, 48, "max", 64, name="in4a")
in4b = InceptionFactory(in4a, 160, 112, 224, 24, 64, "max", 64, name="in4b")
in4c = InceptionFactory(in4b, 128, 128, 256, 24, 64, "max", 64, name="in4c")
in4d = InceptionFactory(in4c, 112, 144, 288, 32, 64, "max", 64, name="in4d")
in4e = InceptionFactory(in4d, 256, 160, 320, 32, 128, "max", 128, name="in4e")
pool5 = mx.sym.Pooling(in4e, kernel=(3, 3), stride=(2, 2), pool_type="max")
in5a = InceptionFactory(pool5, 256, 160, 320, 32, 128, "max", 128, name="in5a")
in5b = InceptionFactory(in5a, 384, 192, 384, 48, 128, "max", 128, name="in5b")
pool6 = mx.sym.Pooling(in5b, kernel=(7, 7), stride=(1,1), global_pool=True, pool_type="avg")
flatten = mx.sym.Flatten(data=pool6)
fc1 = mx.sym.FullyConnected(data=flatten, num_hidden=num_classes)
softmax = mx.symbol.SoftmaxOutput(data=fc1, name='softmax')
return softmax
5.ResNet的实现(2015年)
论文地址:https://arxiv.org/pdf/1512.03385.pdf
网络结构(VGG vs ResNet):


ResNet的发明者是何恺明(Kaiming He)、张翔宇(Xiangyu Zhang)、任少卿(Shaoqing Ren)和孙剑(Jiangxi Sun)。
在2015年的ImageNet大规模视觉识别竞赛(ImageNet Large Scale Visual Recognition Challenge, ILSVRC)中获得了图像分类和物体识别的优胜。 残差网络的特点是容易优化,并且能够通过增加相当的深度来提高准确率。其内部的残差块使用了跳跃连接,缓解了在深度神经网络中增加深度带来的梯度消失问题。
代码实现(symbol):
def residual_unit(data, num_filter, stride, dim_match, name, bottle_neck=True, bn_mom=0.9, workspace=256, memonger=False):
if bottle_neck:
bn1 = mx.sym.BatchNorm(data=data, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn1')
act1 = mx.sym.Activation(data=bn1, act_type='relu', name=name + '_relu1')
conv1 = mx.sym.Convolution(data=act1, num_filter=int(num_filter*0.25), kernel=(1,1), stride=(1,1), pad=(0,0), no_bias=True, workspace=workspace, name=name + '_conv1')
bn2 = mx.sym.BatchNorm(data=conv1, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn2')
act2 = mx.sym.Activation(data=bn2, act_type='relu', name=name + '_relu2')
conv2 = mx.sym.Convolution(data=act2, num_filter=int(num_filter*0.25), kernel=(3,3), stride=stride, pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv2')
bn3 = mx.sym.BatchNorm(data=conv2, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn3')
act3 = mx.sym.Activation(data=bn3, act_type='relu', name=name + '_relu3')
conv3 = mx.sym.Convolution(data=act3, num_filter=num_filter, kernel=(1,1), stride=(1,1), pad=(0,0), no_bias=True, workspace=workspace, name=name + '_conv3')
if dim_match:
shortcut = data
else:
shortcut = mx.sym.Convolution(data=act1, num_filter=num_filter, kernel=(1,1), stride=stride, no_bias=True, workspace=workspace, name=name+'_sc')
if memonger:
shortcut._set_attr(mirror_stage='True')
return conv3 + shortcut
else:
bn1 = mx.sym.BatchNorm(data=data, fix_gamma=False, momentum=bn_mom, eps=2e-5, name=name + '_bn1')
act1 = mx.sym.Activation(data=bn1, act_type='relu', name=name + '_relu1')
conv1 = mx.sym.Convolution(data=act1, num_filter=num_filter, kernel=(3,3), stride=stride, pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv1')
bn2 = mx.sym.BatchNorm(data=conv1, fix_gamma=False, momentum=bn_mom, eps=2e-5, name=name + '_bn2')
act2 = mx.sym.Activation(data=bn2, act_type='relu', name=name + '_relu2')
conv2 = mx.sym.Convolution(data=act2, num_filter=num_filter, kernel=(3,3), stride=(1,1), pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv2')
if dim_match:
shortcut = data
else:
shortcut = mx.sym.Convolution(data=act1, num_filter=num_filter, kernel=(1,1), stride=stride, no_bias=True, workspace=workspace, name=name+'_sc')
if memonger:
shortcut._set_attr(mirror_stage='True')
return conv2 + shortcut
def resnet(units, num_stages, filter_list, num_classes, image_shape, bottle_neck=True, bn_mom=0.9, workspace=256, dtype='float32', memonger=False):
num_unit = len(units)
assert(num_unit == num_stages)
data = mx.sym.Variable(name='data')
if dtype == 'float32':
data = mx.sym.identity(data=data, name='id')
else:
if dtype == 'float16':
data = mx.sym.Cast(data=data, dtype=np.float16)
data = mx.sym.BatchNorm(data=data, fix_gamma=True, eps=2e-5, momentum=bn_mom, name='bn_data')
(nchannel, height, width) = image_shape
if height <= 32: # such as cifar10
body = mx.sym.Convolution(data=data, num_filter=filter_list[0], kernel=(3, 3), stride=(1,1), pad=(1, 1), no_bias=True, name="conv0", workspace=workspace)
else: # often expected to be 224 such as imagenet
body = mx.sym.Convolution(data=data, num_filter=filter_list[0], kernel=(7, 7), stride=(2,2), pad=(3, 3), no_bias=True, name="conv0", workspace=workspace)
body = mx.sym.BatchNorm(data=body, fix_gamma=False, eps=2e-5, momentum=bn_mom, name='bn0')
body = mx.sym.Activation(data=body, act_type='relu', name='relu0')
body = mx.sym.Pooling(data=body, kernel=(3, 3), stride=(2,2), pad=(1,1), pool_type='max')
for i in range(num_stages):
body = residual_unit(body, filter_list[i+1], (1 if i==0 else 2, 1 if i==0 else 2), False, name='stage%d_unit%d' % (i + 1, 1), bottle_neck=bottle_neck, workspace=workspace, memonger=memonger)
for j in range(units[i]-1):
body = residual_unit(body, filter_list[i+1], (1,1), True, name='stage%d_unit%d' % (i + 1, j + 2), bottle_neck=bottle_neck, workspace=workspace, memonger=memonger)
bn1 = mx.sym.BatchNorm(data=body, fix_gamma=False, eps=2e-5, momentum=bn_mom, name='bn1')
relu1 = mx.sym.Activation(data=bn1, act_type='relu', name='relu1')
# Although kernel is not used here when global_pool=True, we should put one
pool1 = mx.sym.Pooling(data=relu1, global_pool=True, kernel=(7, 7), pool_type='avg', name='pool1')
flat = mx.sym.Flatten(data=pool1)
fc1 = mx.sym.FullyConnected(data=flat, num_hidden=num_classes, name='fc1')
if dtype == 'float16':
fc1 = mx.sym.Cast(data=fc1, dtype=np.float32)
return mx.sym.SoftmaxOutput(data=fc1, name='softmax')
def get_symbol(num_classes, num_layers=50, image_shape='3,224,224', conv_workspace=256, dtype='float32', **kwargs):
image_shape = [int(l) for l in image_shape.split(',')]
(nchannel, height, width) = image_shape
if height <= 28:
num_stages = 3
if (num_layers-2) % 9 == 0 and num_layers >= 164:
per_unit = [(num_layers-2)//9]
filter_list = [16, 64, 128, 256]
bottle_neck = True
elif (num_layers-2) % 6 == 0 and num_layers < 164:
per_unit = [(num_layers-2)//6]
filter_list = [16, 16, 32, 64]
bottle_neck = False
else:
raise ValueError("no experiments done on num_layers {}, you can do it yourself".format(num_layers))
units = per_unit * num_stages
else:
if num_layers >= 50:
filter_list = [64, 256, 512, 1024, 2048]
bottle_neck = True
else:
filter_list = [64, 64, 128, 256, 512]
bottle_neck = False
num_stages = 4
if num_layers == 18:
units = [2, 2, 2, 2]
elif num_layers == 34:
units = [3, 4, 6, 3]
elif num_layers == 50:
units = [3, 4, 6, 3]
elif num_layers == 101:
units = [3, 4, 23, 3]
elif num_layers == 152:
units = [3, 8, 36, 3]
elif num_layers == 200:
units = [3, 24, 36, 3]
elif num_layers == 269:
units = [3, 30, 48, 8]
else:
raise ValueError("no experiments done on num_layers {}, you can do it yourself".format(num_layers))
return resnet(units = units,
num_stages = num_stages,
filter_list = filter_list,
num_classes = num_classes,
image_shape = image_shape,
bottle_neck = bottle_neck,
workspace = conv_workspace,
dtype = dtype)
6.MobileNet_V1的实现(2017年)
论文地址:https://arxiv.org/pdf/1704.04861.pdf
网络结构:

MobileNet V1是由google2016年提出,2017年发布的文章。其主要创新点在于深度可分离卷积,而整个网络实际上也是深度可分离模块的堆叠。
深度可分离卷积被证明是轻量化网络的有效设计,深度可分离卷积由逐深度卷积(Depthwise)和逐点卷积(Pointwise)构成。
对比于标准卷积,逐深度卷积将卷积核拆分成为单通道形式,在不改变输入特征图像的深度的情况下,对每一通道进行卷积操作,这样就得到了和输入特征图通道数一致的输出特征图。
逐点卷积就是1×1卷积。主要作用就是对特征图进行升维和降维。
代码实现(symbol):
def Conv(data, num_filter=1, kernel=(1, 1), stride=(1, 1), pad=(0, 0), num_group=1, name='', suffix=''):
conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=kernel, num_group=num_group, stride=stride, pad=pad, no_bias=True, name='%s%s_conv2d' % (name, suffix))
bn = mx.sym.BatchNorm(data=conv, name='%s%s_batchnorm' % (name, suffix), fix_gamma=True)
act = mx.sym.Activation(data=bn, act_type='relu', name='%s%s_relu' % (name, suffix))
return act
def Conv_DPW(data, depth=1, stride=(1, 1), name='', idx=0, suffix=''):
conv_dw = Conv(data, num_group=depth, num_filter=depth, kernel=(3, 3), pad=(1, 1), stride=stride, name="conv_%d_dw" % (idx), suffix=suffix)
conv = Conv(conv_dw, num_filter=depth * stride[0], kernel=(1, 1), pad=(0, 0), stride=(1, 1), name="conv_%d" % (idx), suffix=suffix)
return conv
def get_symbol_compact(num_classes, alpha=1, resolution=224, **kwargs):
assert alpha in alpha_values, 'Invalid alpha={0}, must be one of {1}'.format(alpha, alpha_values)
assert resolution % 32 == 0, 'resolution must be multiple of 32'
base = int(32 * alpha)
data = mx.symbol.Variable(name="data") # 224
conv_1 = Conv(data, num_filter=base, kernel=(3, 3), pad=(1, 1), stride=(2, 2), name="conv_1") # 32*alpha, 224/112
conv_2_dw = Conv(conv_1, num_group=base, num_filter=base, kernel=(3, 3), pad=(1, 1), stride=(1, 1), name="conv_2_dw") # 112/112
conv_2 = Conv(conv_2_dw, num_filter=base * 2, kernel=(1, 1), pad=(0, 0), stride=(1, 1), name="conv_2") # 32*alpha, 112/112
conv_3_dpw = Conv_DPW(conv_2, depth=base * 2, stride=(2, 2), idx=3) # 64*alpha, 112/56 => 56/56
conv_4_dpw = Conv_DPW(conv_3_dpw, depth=base * 4, stride=(1, 1), idx=4) # 128*alpha, 56/56 =>56/56
conv_5_dpw = Conv_DPW(conv_4_dpw, depth=base * 4, stride=(2, 2), idx=5) # 128*alpha, 56/28 => 28/28
conv_6_dpw = Conv_DPW(conv_5_dpw, depth=base * 8, stride=(1, 1), idx=6) # 256*alpha, 28/28 => 28/28
conv_7_dpw = Conv_DPW(conv_6_dpw, depth=base * 8, stride=(2, 2), idx=7) # 256*alpha, 28/14 => 14/14
conv_dpw = conv_7_dpw
for idx in range(8, 13):
conv_dpw = Conv_DPW(conv_dpw, depth=base * 16, stride=(1, 1), idx=idx) # 512*alpha, 14/14
conv_12_dpw = conv_dpw
conv_13_dpw = Conv_DPW(conv_12_dpw, depth=base * 16, stride=(2, 2), idx=13) # 512*alpha, 14/7 => 7/7
conv_14_dpw = Conv_DPW(conv_13_dpw, depth=base * 32, stride=(1, 1), idx=14) # 1024*alpha, 7/7 => 7/7
pool_size = int(resolution / 32)
pool = mx.sym.Pooling(data=conv_14_dpw, kernel=(pool_size, pool_size), stride=(1, 1), pool_type="avg", name="global_pool")
flatten = mx.sym.Flatten(data=pool, name="flatten")
fc = mx.symbol.FullyConnected(data=flatten, num_hidden=num_classes, name='fc')
softmax = mx.symbol.SoftmaxOutput(data=fc, name='softmax')
return softmax
7.MobileNet_V2的实现(2019年)
论文地址:https://arxiv.org/pdf/1801.04381.pdf
网络结构:

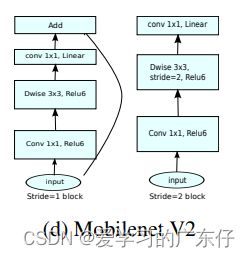
mobilenetV1的缺点:
- V1结构过于简单,没有复用图像特征,即没有concat/eltwise+ 等操作进行特征融合,而后续的一系列的ResNet, DenseNet等结构已经证明复用图像特征的有效性。
- 在处理低维数据(比如逐深度的卷积)时,relu函数会造成信息的丢失。
- DW 卷积由于本身的计算特性决定它自己没有改变通道数的能力,上一层给它多少通道,它就只能输出多少通道。所以如果上一层给的通道数本身很少的话,DW 也只能很委屈的在低维空间提特征,因此效果不够好。
V2使用了跟V1类似的深度可分离结构,不同之处也正对应着V1中逐深度卷积的缺点改进:
- V2 去掉了第二个 PW 的激活函数改为线性激活。
- V2 在 DW 卷积之前新加了一个 PW 卷积。
代码实现(symbol):
class MobileNetV2(nn.HybridBlock):
def __init__(self, multiplier=1.0, classes=1000, **kwargs):
super(MobileNetV2, self).__init__(**kwargs)
with self.name_scope():
self.features = nn.HybridSequential(prefix='features_')
with self.features.name_scope():
_add_conv(self.features, int(32 * multiplier), kernel=3,
stride=2, pad=1, relu6=True)
in_channels_group = [int(x * multiplier) for x in [32] + [16] + [24] * 2
+ [32] * 3 + [64] * 4 + [96] * 3 + [160] * 3]
channels_group = [int(x * multiplier) for x in [16] + [24] * 2 + [32] * 3
+ [64] * 4 + [96] * 3 + [160] * 3 + [320]]
ts = [1] + [6] * 16
strides = [1, 2] * 2 + [1, 1, 2] + [1] * 6 + [2] + [1] * 3
for in_c, c, t, s in zip(in_channels_group, channels_group, ts, strides):
self.features.add(LinearBottleneck(in_channels=in_c, channels=c,
t=t, stride=s))
last_channels = int(1280 * multiplier) if multiplier > 1.0 else 1280
_add_conv(self.features, last_channels, relu6=True)
self.features.add(nn.GlobalAvgPool2D())
self.output = nn.HybridSequential(prefix='output_')
with self.output.name_scope():
self.output.add(
nn.Conv2D(classes, 1, use_bias=False, prefix='pred_'),
nn.Flatten()
)
def hybrid_forward(self, F, x):
x = self.features(x)
x = self.output(x)
return x
def get_symbol(num_classes=1000, multiplier=1.0, ctx=mx.cpu(), **kwargs):
net = MobileNetV2(multiplier=multiplier, classes=num_classes, **kwargs)
net.initialize(ctx=ctx, init=mx.init.Xavier())
net.hybridize()
data = mx.sym.var('data')
out = net(data)
sym = mx.sym.SoftmaxOutput(out, name='softmax')
return sym
8.ResNext的实现(2016年)
论文地址:https://arxiv.org/pdf/1611.05431.pdf
网络结构:

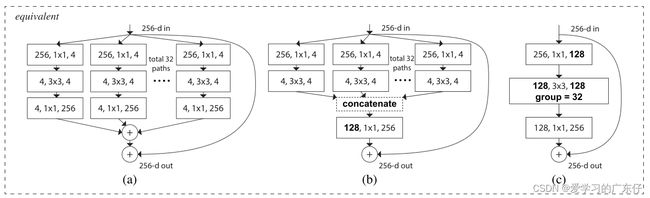
ResNeXt对ResNet进行了改进,采用了多分支的策略,在论文中作者提出了三种等价的模型结构,最后的ResNeXt用了C的结构来构建我们的ResNeXt、这里面和我们的Inception是不同的,在Inception中,每一部分的拓扑结构是不同的,比如一部分是1x1卷积,3x3卷积还有5x5卷积,而我们ResNeXt是用相同的拓扑结构,并在保持参数量的情况下提高了准确率。
代码实现(symbol):
def residual_unit(data, num_filter, stride, dim_match, name, bottle_neck=True, num_group=32, bn_mom=0.9, workspace=256, memonger=False):
if bottle_neck:
conv1 = mx.sym.Convolution(data=data, num_filter=int(num_filter*0.5), kernel=(1,1), stride=(1,1), pad=(0,0), no_bias=True, workspace=workspace, name=name + '_conv1')
bn1 = mx.sym.BatchNorm(data=conv1, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn1')
act1 = mx.sym.Activation(data=bn1, act_type='relu', name=name + '_relu1')
conv2 = mx.sym.Convolution(data=act1, num_filter=int(num_filter*0.5), num_group=num_group, kernel=(3,3), stride=stride, pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv2')
bn2 = mx.sym.BatchNorm(data=conv2, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn2')
act2 = mx.sym.Activation(data=bn2, act_type='relu', name=name + '_relu2')
conv3 = mx.sym.Convolution(data=act2, num_filter=num_filter, kernel=(1,1), stride=(1,1), pad=(0,0), no_bias=True, workspace=workspace, name=name + '_conv3')
bn3 = mx.sym.BatchNorm(data=conv3, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_bn3')
if dim_match:
shortcut = data
else:
shortcut_conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=(1,1), stride=stride, no_bias=True, workspace=workspace, name=name+'_sc')
shortcut = mx.sym.BatchNorm(data=shortcut_conv, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_sc_bn')
if memonger:
shortcut._set_attr(mirror_stage='True')
eltwise = bn3 + shortcut
return mx.sym.Activation(data=eltwise, act_type='relu', name=name + '_relu')
else:
conv1 = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=(3,3), stride=stride, pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv1')
bn1 = mx.sym.BatchNorm(data=conv1, fix_gamma=False, momentum=bn_mom, eps=2e-5, name=name + '_bn1')
act1 = mx.sym.Activation(data=bn1, act_type='relu', name=name + '_relu1')
conv2 = mx.sym.Convolution(data=act1, num_filter=num_filter, kernel=(3,3), stride=(1,1), pad=(1,1), no_bias=True, workspace=workspace, name=name + '_conv2')
bn2 = mx.sym.BatchNorm(data=conv2, fix_gamma=False, momentum=bn_mom, eps=2e-5, name=name + '_bn2')
if dim_match:
shortcut = data
else:
shortcut_conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=(1,1), stride=stride, no_bias=True, workspace=workspace, name=name+'_sc')
shortcut = mx.sym.BatchNorm(data=shortcut_conv, fix_gamma=False, eps=2e-5, momentum=bn_mom, name=name + '_sc_bn')
if memonger:
shortcut._set_attr(mirror_stage='True')
eltwise = bn2 + shortcut
return mx.sym.Activation(data=eltwise, act_type='relu', name=name + '_relu')
def resnext(units, num_stages, filter_list, num_classes, num_group, image_shape, bottle_neck=True, bn_mom=0.9, workspace=256, dtype='float32', memonger=False):
num_unit = len(units)
assert(num_unit == num_stages)
data = mx.sym.Variable(name='data')
if dtype == 'float32':
data = mx.sym.identity(data=data, name='id')
else:
if dtype == 'float16':
data = mx.sym.Cast(data=data, dtype=np.float16)
data = mx.sym.BatchNorm(data=data, fix_gamma=True, eps=2e-5, momentum=bn_mom, name='bn_data')
(nchannel, height, width) = image_shape
if height <= 32: # such as cifar10
body = mx.sym.Convolution(data=data, num_filter=filter_list[0], kernel=(3, 3), stride=(1,1), pad=(1, 1), no_bias=True, name="conv0", workspace=workspace)
else: # often expected to be 224 such as imagenet
body = mx.sym.Convolution(data=data, num_filter=filter_list[0], kernel=(7, 7), stride=(2,2), pad=(3, 3), no_bias=True, name="conv0", workspace=workspace)
body = mx.sym.BatchNorm(data=body, fix_gamma=False, eps=2e-5, momentum=bn_mom, name='bn0')
body = mx.sym.Activation(data=body, act_type='relu', name='relu0')
body = mx.sym.Pooling(data=body, kernel=(3, 3), stride=(2,2), pad=(1,1), pool_type='max')
for i in range(num_stages):
body = residual_unit(body, filter_list[i+1], (1 if i==0 else 2, 1 if i==0 else 2), False, name='stage%d_unit%d' % (i + 1, 1), bottle_neck=bottle_neck, num_group=num_group, bn_mom=bn_mom, workspace=workspace, memonger=memonger)
for j in range(units[i]-1):
body = residual_unit(body, filter_list[i+1], (1,1), True, name='stage%d_unit%d' % (i + 1, j + 2), bottle_neck=bottle_neck, num_group=num_group, bn_mom=bn_mom, workspace=workspace, memonger=memonger)
pool1 = mx.sym.Pooling(data=body, global_pool=True, kernel=(7, 7), pool_type='avg', name='pool1')
flat = mx.sym.Flatten(data=pool1)
fc1 = mx.sym.FullyConnected(data=flat, num_hidden=num_classes, name='fc1')
if dtype == 'float16':
fc1 = mx.sym.Cast(data=fc1, dtype=np.float32)
return mx.sym.SoftmaxOutput(data=fc1, name='softmax')
def get_symbol(num_classes, num_layers=50, image_shape='3,224,224', num_group=32, conv_workspace=256, dtype='float32', **kwargs):
image_shape = [int(l) for l in image_shape.split(',')]
(nchannel, height, width) = image_shape
if height <= 32:
num_stages = 3
if (num_layers-2) % 9 == 0 and num_layers >= 164:
per_unit = [(num_layers-2)//9]
filter_list = [16, 64, 128, 256]
bottle_neck = True
elif (num_layers-2) % 6 == 0 and num_layers < 164:
per_unit = [(num_layers-2)//6]
filter_list = [16, 16, 32, 64]
bottle_neck = False
else:
raise ValueError("no experiments done on num_layers {}, you can do it yourself".format(num_layers))
units = per_unit * num_stages
else:
if num_layers >= 50:
filter_list = [64, 256, 512, 1024, 2048]
bottle_neck = True
else:
filter_list = [64, 64, 128, 256, 512]
bottle_neck = False
num_stages = 4
if num_layers == 18:
units = [2, 2, 2, 2]
elif num_layers == 34:
units = [3, 4, 6, 3]
elif num_layers == 50:
units = [3, 4, 6, 3]
elif num_layers == 101:
units = [3, 4, 23, 3]
elif num_layers == 152:
units = [3, 8, 36, 3]
elif num_layers == 200:
units = [3, 24, 36, 3]
elif num_layers == 269:
units = [3, 30, 48, 8]
else:
raise ValueError("no experiments done on num_layers {}, you can do it yourself".format(num_layers))
return resnext(units = units,
num_stages = num_stages,
filter_list = filter_list,
num_classes = num_classes,
num_group = num_group,
image_shape = image_shape,
bottle_neck = bottle_neck,
workspace = conv_workspace,
dtype = dtype)
9.inception_V4的实现(2016年)
论文地址:https://arxiv.org/pdf/1602.07261.pdf
网络结构:

一方面,我们考虑将最新的两个思想(Inception结构和ResNet结构)结合在一起。ResNet的作者认为在很深的网络中使用ResNet是十分必要的,而Inception结构又倾向于很深,所以我们很自然的想把Inception中的串联用Residual connection替代。这可以让Inception获得Residual connection的优点而又保持它本身的计算效率。
另一方面,我们考虑是否可以通过将网络变宽和变深提升最终效果。Inception V3带着很多之前阶段的包袱。最重要的技术限制是使用DistBelief做分布式训练需要对模型进行划分。
代码实现(symbol):
def Conv(data, num_filter, kernel=(1, 1), stride=(1, 1), pad=(0, 0), name=None, suffix=''):
conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=kernel, stride=stride, pad=pad, no_bias=True, name='%s%s_conv2d' %(name, suffix))
bn = mx.sym.BatchNorm(data=conv, name='%s%s_batchnorm' %(name, suffix), fix_gamma=True)
act = mx.sym.Activation(data=bn, act_type='relu', name='%s%s_relu' %(name, suffix))
return act
def Inception_stem(data, name= None):
c = Conv(data, 32, kernel=(3, 3), stride=(2, 2), name='%s_conv1_3*3' %name)
c = Conv(c, 32, kernel=(3, 3), name='%s_conv2_3*3' %name)
c = Conv(c, 64, kernel=(3, 3), pad=(1, 1), name='%s_conv3_3*3' %name)
p1 = mx.sym.Pooling(c, kernel=(3, 3), stride=(2, 2), pool_type='max', name='%s_maxpool_1' %name)
c2 = Conv(c, 96, kernel=(3, 3), stride=(2, 2), name='%s_conv4_3*3' %name)
concat = mx.sym.Concat(*[p1, c2], name='%s_concat_1' %name)
c1 = Conv(concat, 64, kernel=(1, 1), pad=(0, 0), name='%s_conv5_1*1' %name)
c1 = Conv(c1, 96, kernel=(3, 3), name='%s_conv6_3*3' %name)
c2 = Conv(concat, 64, kernel=(1, 1), pad=(0, 0), name='%s_conv7_1*1' %name)
c2 = Conv(c2, 64, kernel=(7, 1), pad=(3, 0), name='%s_conv8_7*1' %name)
c2 = Conv(c2, 64, kernel=(1, 7), pad=(0, 3), name='%s_conv9_1*7' %name)
c2 = Conv(c2, 96, kernel=(3, 3), pad=(0, 0), name='%s_conv10_3*3' %name)
concat = mx.sym.Concat(*[c1, c2], name='%s_concat_2' %name)
c1 = Conv(concat, 192, kernel=(3, 3), stride=(2, 2), name='%s_conv11_3*3' %name)
p1 = mx.sym.Pooling(concat, kernel=(3, 3), stride=(2, 2), pool_type='max', name='%s_maxpool_2' %name)
concat = mx.sym.Concat(*[c1, p1], name='%s_concat_3' %name)
return concat
def InceptionA(input, name=None):
p1 = mx.sym.Pooling(input, kernel=(3, 3), pad=(1, 1), pool_type='avg', name='%s_avgpool_1' %name)
c1 = Conv(p1, 96, kernel=(1, 1), pad=(0, 0), name='%s_conv1_1*1' %name)
c2 = Conv(input, 96, kernel=(1, 1), pad=(0, 0), name='%s_conv2_1*1' %name)
c3 = Conv(input, 64, kernel=(1, 1), pad=(0, 0), name='%s_conv3_1*1' %name)
c3 = Conv(c3, 96, kernel=(3, 3), pad=(1, 1), name='%s_conv4_3*3' %name)
c4 = Conv(input, 64, kernel=(1, 1), pad=(0, 0), name='%s_conv5_1*1' % name)
c4 = Conv(c4, 96, kernel=(3, 3), pad=(1, 1), name='%s_conv6_3*3' % name)
c4 = Conv(c4, 96, kernel=(3, 3), pad=(1, 1), name='%s_conv7_3*3' %name)
concat = mx.sym.Concat(*[c1, c2, c3, c4], name='%s_concat_1' %name)
return concat
def ReductionA(input, name=None):
p1 = mx.sym.Pooling(input, kernel=(3, 3), stride=(2, 2), pool_type='max', name='%s_maxpool_1' %name)
c2 = Conv(input, 384, kernel=(3, 3), stride=(2, 2), name='%s_conv1_3*3' %name)
c3 = Conv(input, 192, kernel=(1, 1), pad=(0, 0), name='%s_conv2_1*1' %name)
c3 = Conv(c3, 224, kernel=(3, 3), pad=(1, 1), name='%s_conv3_3*3' %name)
c3 = Conv(c3, 256, kernel=(3, 3), stride=(2, 2), pad=(0, 0), name='%s_conv4_3*3' %name)
concat = mx.sym.Concat(*[p1, c2, c3], name='%s_concat_1' %name)
return concat
def InceptionB(input, name=None):
p1 = mx.sym.Pooling(input, kernel=(3, 3), pad=(1, 1), pool_type='avg', name='%s_avgpool_1' %name)
c1 = Conv(p1, 128, kernel=(1, 1), pad=(0, 0), name='%s_conv1_1*1' %name)
c2 = Conv(input, 384, kernel=(1, 1), pad=(0, 0), name='%s_conv2_1*1' %name)
c3 = Conv(input, 192, kernel=(1, 1), pad=(0, 0), name='%s_conv3_1*1' %name)
c3 = Conv(c3, 224, kernel=(1, 7), pad=(0, 3), name='%s_conv4_1*7' %name)
#paper wrong
c3 = Conv(c3, 256, kernel=(7, 1), pad=(3, 0), name='%s_conv5_1*7' %name)
c4 = Conv(input, 192, kernel=(1, 1), pad=(0, 0), name='%s_conv6_1*1' %name)
c4 = Conv(c4, 192, kernel=(1, 7), pad=(0, 3), name='%s_conv7_1*7' %name)
c4 = Conv(c4, 224, kernel=(7, 1), pad=(3, 0), name='%s_conv8_7*1' %name)
c4 = Conv(c4, 224, kernel=(1, 7), pad=(0, 3), name='%s_conv9_1*7' %name)
c4 = Conv(c4, 256, kernel=(7, 1), pad=(3, 0), name='%s_conv10_7*1' %name)
concat = mx.sym.Concat(*[c1, c2, c3, c4], name='%s_concat_1' %name)
return concat
def ReductionB(input,name=None):
p1 = mx.sym.Pooling(input, kernel=(3, 3), stride=(2, 2), pool_type='max', name='%s_maxpool_1' %name)
c2 = Conv(input, 192, kernel=(1, 1), pad=(0, 0), name='%s_conv1_1*1' %name)
c2 = Conv(c2, 192, kernel=(3, 3), stride=(2, 2), name='%s_conv2_3*3' %name)
c3 = Conv(input, 256, kernel=(1, 1), pad=(0, 0), name='%s_conv3_1*1' %name)
c3 = Conv(c3, 256, kernel=(1, 7), pad=(0, 3), name='%s_conv4_1*7' %name)
c3 = Conv(c3, 320, kernel=(7, 1), pad=(3, 0), name='%s_conv5_7*1' %name)
c3 = Conv(c3, 320, kernel=(3, 3), stride=(2, 2), name='%s_conv6_3*3' %name)
concat = mx.sym.Concat(*[p1, c2, c3], name='%s_concat_1' %name)
return concat
def InceptionC(input, name=None):
p1 = mx.sym.Pooling(input, kernel=(3, 3), pad=(1, 1), pool_type='avg', name='%s_avgpool_1' %name)
c1 = Conv(p1, 256, kernel=(1, 1), pad=(0, 0), name='%s_conv1_1*1' %name)
c2 = Conv(input, 256, kernel=(1, 1), pad=(0, 0), name='%s_conv2_1*1' %name)
c3 = Conv(input, 384, kernel=(1, 1), pad=(0, 0), name='%s_conv3_1*1' %name)
c3_1 = Conv(c3, 256, kernel=(1, 3), pad=(0, 1), name='%s_conv4_3*1' %name)
c3_2 = Conv(c3, 256, kernel=(3, 1), pad=(1, 0), name='%s_conv5_1*3' %name)
c4 = Conv(input, 384, kernel=(1, 1), pad=(0, 0), name='%s_conv6_1*1' %name)
c4 = Conv(c4, 448, kernel=(1, 3), pad=(0, 1), name='%s_conv7_1*3' %name)
c4 = Conv(c4, 512, kernel=(3, 1), pad=(1, 0), name='%s_conv8_3*1' %name)
c4_1 = Conv(c4, 256, kernel=(3, 1), pad=(1, 0), name='%s_conv9_1*3' %name)
c4_2 = Conv(c4, 256, kernel=(1, 3), pad=(0, 1), name='%s_conv10_3*1' %name)
concat = mx.sym.Concat(*[c1, c2, c3_1, c3_2, c4_1, c4_2], name='%s_concat' %name)
return concat
def get_symbol(num_classes=1000, dtype='float32'):
data = mx.sym.Variable(name="data")
if dtype == 'float32':
data = mx.sym.identity(data=data, name='id')
else:
if dtype == 'float16':
data = mx.sym.Cast(data=data, dtype=np.float16)
x = Inception_stem(data, name='in_stem')
#4 * InceptionA
# x = InceptionA(x, name='in1A')
# x = InceptionA(x, name='in2A')
# x = InceptionA(x, name='in3A')
# x = InceptionA(x, name='in4A')
for i in range(4):
x = InceptionA(x, name='in%dA' %(i+1))
#Reduction A
x = ReductionA(x, name='re1A')
#7 * InceptionB
# x = InceptionB(x, name='in1B')
# x = InceptionB(x, name='in2B')
# x = InceptionB(x, name='in3B')
# x = InceptionB(x, name='in4B')
# x = InceptionB(x, name='in5B')
# x = InceptionB(x, name='in6B')
# x = InceptionB(x, name='in7B')
for i in range(7):
x = InceptionB(x, name='in%dB' %(i+1))
#ReductionB
x = ReductionB(x, name='re1B')
#3 * InceptionC
# x = InceptionC(x, name='in1C')
# x = InceptionC(x, name='in2C')
# x = InceptionC(x, name='in3C')
for i in range(3):
x = InceptionC(x, name='in%dC' %(i+1))
#Average Pooling
x = mx.sym.Pooling(x, kernel=(8, 8), pad=(1, 1), pool_type='avg', name='global_avgpool')
#Dropout
x = mx.sym.Dropout(x, p=0.2)
flatten = mx.sym.Flatten(x, name='flatten')
fc1 = mx.sym.FullyConnected(flatten, num_hidden=num_classes, name='fc1')
if dtype == 'float16':
fc1 = mx.sym.Cast(data=fc1, dtype=np.float32)
softmax = mx.sym.SoftmaxOutput(fc1, name='softmax')
return softmax
二、数据集的准备
1.数据集描述
因ImageNet数据集过于庞大,在学习训练上比较费资源,因此本次数据集使用中国象棋数据集,中国象棋红黑棋子一共有14种类,经过预处理后会得到单独象棋图像,如图:
![]()
2.数据集准备
数据集主要以文件夹形式进行区分,每一个类别代表一个文件夹,如图:
![]()
在训练的时候直接把此文件夹目录放入代码中即可,对于训练集和验证集,代码会在这里的文件夹中做一个根据提供的划分比例随机拆分。
三、模型训练
1.数据加载器
这里会生成mxnet的数据集的格式
def get_iterator(DataDir, batch_size, data_shape, ratio=0.9):
classes,num_data = get_list(DataDir,ratio)
eigval = np.array([55.46, 4.794, 1.148])
eigvec = np.array([[-0.5675, 0.7192, 0.4009], [-0.5808, -0.0045, -0.8140], [-0.5836, -0.6948, 0.4203]])
shape_ = data_shape
shape = (3, data_shape, data_shape)
aug_list_test = [mx.image.ForceResizeAug(size=(shape_, shape_)), mx.image.CenterCropAug((shape_, shape_)),]
aug_list_train = [
mx.image.ForceResizeAug(size=(shape_, shape_)),
mx.image.RandomCropAug((shape_, shape_)),
mx.image.HorizontalFlipAug(0.5),
mx.image.CastAug(),
mx.image.ColorJitterAug(0.0, 0.1, 0.1),
mx.image.HueJitterAug(0.5),
mx.image.LightingAug(0.1, eigval, eigvec),
# RandomRotateAug(30, 0.5),
# RandomNoiseAug(10,0.5)
]
train_iter = mx.image.ImageIter(batch_size=batch_size,
data_shape=shape,
label_width=1,
aug_list=aug_list_train,
shuffle=True,
path_root='',
path_imglist='./train.dat',
)
val_iter = mx.image.ImageIter(batch_size=batch_size,
data_shape=shape,
label_width=1,
shuffle=False,
aug_list=aug_list_test,
path_root='',
path_imglist='./val.dat',
)
return custom_iter(train_iter), custom_iter(val_iter), classes, num_data
2.mxnet模型初始化
if USEGPU:
self.ctx = mx.gpu()
else:
self.ctx = mx.cpu()
self.batch_size = batch_size
self.train_iter, self.val_iter,self.classes_names,self.num_trainData = get_iterator(DataDir, batch_size, self.image_size, ratio)
self.model = get_symbol(len(self.classes_names))
这里的get_symbol函数就是可以根据前面的模型介绍进行修改即可
3.学习率的设置
lr_scheduler = mx.lr_scheduler.FactorScheduler(int(TrainNum*self.num_trainData/4), 0.9)
4.断点设置
这里是训练的时候设置模型的保存
epoch_end_callback = mx.callback.do_checkpoint(os.path.join(ModelPath,'model'), CheckPoint)
5.模型训练
mod = mx.mod.Module(symbol=self.model,
context=self.ctx,
data_names=['data'],
label_names=['softmax_label'])
mod.fit(self.train_iter, self.val_iter,
num_epoch=TrainNum,
allow_missing=True,
batch_end_callback=mx.callback.Speedometer(self.batch_size, 5),
epoch_end_callback=epoch_end_callback,
kvstore='device',
optimizer='sgd',
optimizer_params={
'learning_rate': learning_rate,
'momentum': 0.9,
'lr_scheduler': lr_scheduler,
'wd': 0.005
},
initializer=mx.init.Xavier(factor_type="in", magnitude=2.34),
eval_metric='acc')
四、模型预测
这里根据模型的训练逻辑写预测代码即可
def predict(self,image):
img = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
if img is None:
return None
img = cv2.resize(img, (224, 224))
img = np.swapaxes(img, 0, 2)
img = np.swapaxes(img, 1, 2)
img = img[np.newaxis, :]
self.mod.forward(self.Batch([mx.nd.array(img)]))
prob = self.mod.get_outputs()[0].asnumpy()
prob = np.squeeze(prob)
a = np.argsort(prob)[::-1]
predict_res={}
for each_index in range(0,len(self.classes_names)):
predict_res[self.classes_names[str(a[each_index])]] = prob[a[each_index]]
return self.classes_names[str(a[0])],predict_res
五、模型主入口
if __name__ == '__main__':
ctu = Ctu_Classification()
ctu.InitModel('./data',batch_size=4,ratio=0.9)
ctu.train(TrainNum=300,learning_rate=0.001,ModelPath='./Model2',CheckPoint=10)
# ctu = Ctu_Classification()
# ctu.LoadModel(r'./Model/model-0300.params',r'./Model/model-symbol.json',r'./Model/class_index.json')
# cv2.namedWindow("origin", 0)
# cv2.resizeWindow("origin", 640, 480)
# for root, dirs, files in os.walk(r"D:\Ctu\Ctu_Project_DL\Ctu_Mxnet_DL\Classification\symbol_版本\data\黑将"):
# for f in files:
# img_cv = ctu.cv2_imread(os.path.join(root, f), is_color=True, model=True)
# class_names , predict_res = ctu.predict(img_cv)
# print(class_names , predict_res)
# cv2.imshow("origin", img_cv)
# cv2.waitKey()
# del ctu
总结
symbol版本在加载模型中本人稍作了一些修改,修改内容如下
# 在源码文件:C:\python38\Lib\site-packages\mxnet\model.py 中添加以下函数
# def Ctu_LoadModel(ModelFile, JsonFile):
# symbol = sym.load(JsonFile)
#
# save_dict = nd.load(ModelFile)
# arg_params = {}
# aux_params = {}
# if not save_dict:
# logging.warning("Params file '%s' is empty", '%s-%04d.params' % (prefix, epoch))
# return (arg_params, aux_params)
# for k, v in save_dict.items():
# tp, name = k.split(":", 1)
# if tp == "arg":
# arg_params[name] = v
# if tp == "aux":
# aux_params[name] = v
#
# return (symbol, arg_params, aux_params)