Python之Numpy，从0到掌握（偏向实战+源码+赛前抱佛脚）

前言

1、本篇偏向实战，相关理论知识我会后续补充

2、本人平时喜欢看函数源码，所以基本所有格式，情况都有写（没写就是源码没写）

NumPy介绍

NumPy是python语言的第三方库，支持大量高维度的数组和矩阵计算，此外，numpy也针对数组提供了大量的数学函数，机器学习涉及大量对数组的变换和运算，numpy就成了必不可少的工具之一。

一、如何创建

1、导入numpy库，并为了方便命名为 np

import numpy as np

2、查看版本

np.__version__

我的是 1.21.4 版本

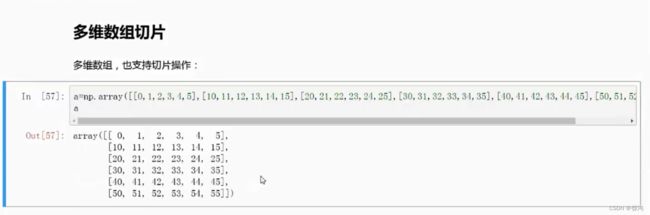
3、创建数组

Numpy的主要对象是多维数组ndarray。

• 在numpy中维度叫做轴
• 轴的个数叫做秩
  值得注意的是，numpy.array和Python 标准库 array.array 并不相同前者更为强大，这也就是我们学习 NumPy 的重要原因之一。

通过列表创建一维数组

arr1 = np.array([1,2,3])
print(arr1)

[1 2 3]

那上面的数组就是一个秩为1的数组（这里我们可以简单理解为维度），因为他只有一个轴，而且长度为3

通过列表创建二维数组

# 通过列表创建二维数组
arr2 = np.array([ [1,2,3] , [4,5,6]  ,[6,7,8] ])
print(arr2)

[[1 2 3]
 [4 5 6]
 [6 7 8]]

zeros：创建全为0 的数组

zeros：生成指定行数、列数并且全为0的n维数组
可以只写一个，那就是一维数组
zeros（ （行，列））
你行列写成几维他就是几维度，下面几个函数也是，我懒，懒得都写！

zeros1 = np.zeros( (3,4))
print(zeros1)


[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]

ones：创建全为1的数组

ones1 = np.ones(  (2,2,2) )
print(ones1)

[[[1. 1.]
  [1. 1.]]

 [[1. 1.]
  [1. 1.]]]   
  没怎么弄过三维的我就勉强优化一下形式，这下看得懂了是吧？：
  [
    [
        [1. 1.]，
        [1. 1.]
     ]，
     [
        [1. 1.]，
        [1. 1.]
     ]
]  

linspace：生成等差数列

左闭右闭
linspace（start，end，num）

a= np.linspace(1,10,10)
print(a)

[ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]

三维数组的理解

三维数组

full：创建可以自定义维度 和 填充数字 的数组

full1 = np.full( (2,3),1 )
print(full1)


[[1 1 1]
 [1 1 1]]

arange：创建一维等差（元素值从0到自定义数字减一）

写到这的时候，真的给我整笑了，我是看别人的文章然后在自己总结，我看到这题目给我弄不会了，等差数组？难道是设置范围他自己给我生成？然后我去试了试，就是：

• 首先：创建一维数组，变不了
• 其次：我看了源码，他是只有一个start参数的，所以起始值定了 为0 ， 我们只需要传递终止值就是，此处需注意，生成的范围减了一，和python里的range函数如出一辙！

arange1 = np.arange(5)
print(arange1)

[0 1 2 3 4]

reshape：不改变数据的条件下，修改数组形状（接上面的创建一维，有笑点）

首先，聪明的csdn友肯定会想，那怎么创建二维的等差呢？
当然可以！
那么，对应的函数是什么呢？我也不知道。
我又是看得别人文章，先给你们看他的答案：

np.arange(6).reshape(2, 3)

厉害吗？
我当时看懂了之后，我觉得，这哥们不知道是真的不懂reshape，还是把这条代码说的和上面显得更贴切一点。总结来说上面两个的代码，就是这个问题：
arange(n).reshape(a, b) 依次生成n个自然数（值域是0到n-1），并且以a行b列的数组形式显示

ok，不谈了，进入正题：

首先来看reshape函数（不改变数据的条件下，修改形状）的源码：

1. 此处是数组名.reshape（）形式

reshape(self, shape, order='C')

• shape：你们都是知道的，就是形状，几行几列
• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘k’ – 元素在内存中的出现顺序。
  来看实例：

reshape2 = np.arange(4)
reshape2 = reshape2.reshape(2,2,order='C')
print(reshape2)

[[0 1]
 [2 3]]

2. 第二种
   菜鸟教程：numpy.reshape(arr, newshape, order=‘C’)

• arr：要修改形状的数组
• newshape：整数或者整数数组，新的形状应当兼容原有形状
• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘k’ – 元素在内存中的出现顺序。

实例：

reshape1 = np.reshape(np.arange(4), (2,2), order='C')
print(reshape1)

[[0 1]
 [2 3]]

好，一般的博主在现在都会跳过，但是，我不会，因为，你们真的懂order取值的概念吗？反正我是不懂，我也才学,so,我去试了试
直接给你们看代码，我把源数据变为了：

reshape1 = np.reshape(np.arange(9), (3,3), order='c')

1. 当order为c，也就是按行时：

[[0 1 2]
 [3 4 5]
 [6 7 8]]

2. 为f时，也就是按列时：

[[0 3 6]
 [1 4 7]
 [2 5 8]]

3. 为a时，也就是原顺序：

[[0 1 2]
 [3 4 5]
 [6 7 8]]

4. 为k时，也就是为内存中的数据：
   朋友们，源码真的是个好东西，我写成k，他就报错！
   
   我他喵的，搜了好久，才发现reshape的源码里面是这样写得！
   

k不在了！估计是新版的问题，我的版本是1.23.1，估计更新了，没了就更棒了~

不用我说，你们看了上面几种的对比也知道了对吧。

-----------------------------------------------------------------

看了看其他大佬的文章，我觉得我写文章写得慢，有好处也有坏处，好处是想得周到，自己不会的，想到的都会去求解，但是慢在写文章太拖沓，像在写小说一样，所以，下面的文章，我就改变一下，so，希望你们看得懂

random.rand：创建随机二维数组

np.random.rand(shape)

• 范围： [0,1) 源码：↓
  

np.random.rand(2, 2)

[[0.16403419 0.67808061]
 [0.04344741 0.19238262]]

创建n维随机数组

重点是随机
随机类：random
首先，满足随机的有以下函数：

1. rand :产生n维，源码里面范围
   

2. random：只能产生一维，范围：

3. randint: 可以创建n维度，看源码：
   made。懒得给你们截图，我直接给你们源码的结论：
   randint(low, high=None, size=None, dtype=None):

• 省略high，返回的范围：[0, low)
• low，high都写，返回的范围：[low, high)
• size：就是shape,形状

实例：

random2 = np.random.randint(4,size=(2,2))
random3 = np.random.rand(2,2)
random4 = np.random.random(3)


print(random2)
print("____")
print(random3)
print("____")
print(random4)


[[3 2]
 [2 0]]
____
[[0.71634611 0.22716593]
 [0.80354273 0.36203558]]
____
[0.75746996 0.56738677 0.40173797]

二、数组运算

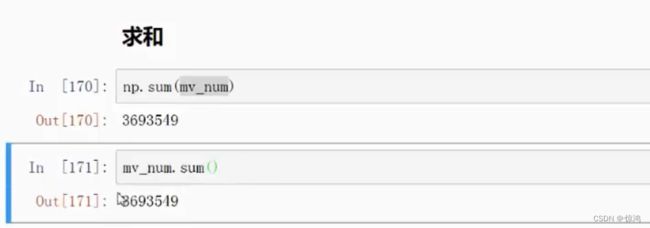
sum：数组元素累加值

总结：
sum函数不仅可以计算数组元素累加值，而且还可以每一列or每一行单独求和。
实例：

a = np.array([[1, 2],
              [3, 4]])
print(a)
print(np.sum(a))
print(np.sum(a, axis=0)) # axis=0 表示对每一列求和

print(np.sum(a, axis=1)) # axis=0 表示对每一行求和

[[1 2]
 [3 4]]
10
[4 6]
[3 7]

mean：数组元素平均值

总结：
sum函数不仅可以计算数组元素平均值，而且还可以每一列or每一行单独求平均值。
实例

a = np.array([[1, 2],
              [3, 4]])
print(np.mean(a)) # 求取平均值
print(np.mean(a,axis=1)) # 对每一行 求取平均值
print(np.mean(a,axis=0)) # 对每一列 求取平均值

2.5
[1.5 3.5]
[2. 3.]

tile：横、纵向平铺数组

格式：tile(a,shape)
看了下源码，我英文差，就没写百分之100的情况：
简单来说，就是把 a 当作我们的元素，去构造一个 形状为shape的数组
实例

a = np.array([[1, 2],
              [3, 4]])
print( np.tile(a,2)  )
print("-----")
print( np.tile( a,(2,2) ) )

[[1 2 1 2]
 [3 4 3 4]]
-----
[[1 2 1 2]
 [3 4 3 4]
 [1 2 1 2]
 [3 4 3 4]]

• 只有一个参数，就向右平铺，此处我就懒得说x轴 or y轴了

argsort：将元素按照行从小到大排序，返回对应位置元素的下标

源码简单不用看

实例

a = np.array([[1, 2, 3,  4],
              [8, 7, 6, 5]])
print(a.argsort(axis=-1))# axis= 1 or -1 将元素按照 行  从小到大排序，返回对应位置元素的下标
print("-------")
print(a.argsort(axis=0))# axis= 0  or -2 将元素按照 列  从小到大排序，返回对应位置元素的下标
这里的取值，1和-2是我自己试出来的，网上很多都只写了-1 和 0 

[[0 1 2 3]
 [3 2 1 0]]
-------
[[0 0 0 0]
 [1 1 1 1]]

n维数组加、减、乘、除运算

这玩意我想都不用想，没看源码,不管几维度，都一样算法

• 就是相应位置上的加减乘除而已，
• 然后我去试了试shape不相同的情况，当其中一个是一维的时候，他会应用到另一个数组的每一行上

实例

a = np.array([[1, 2],
              [3, 4]])

b = np.array([[5, 6],
              [7, 8]])
print(a + b)
print("-"*6)
print(a - b)
print("-"*6)
print(a * b)
print("-"*6)
print(a / b)



[[ 6  8]
 [10 12]]
------
[[-4 -4]
 [-4 -4]]
------
[[ 5 12]
 [21 32]]
------
[[0.2        0.33333333]
 [0.42857143 0.5       ]]
特殊情况：
a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]])

b = np.array([1, 2, 3])
print(a + b)


[[ 2  4  6]
 [ 5  7  9]
 [ 8 10 12]]

矩阵乘法运算

矩阵部分，这里直接看例子，后面我会补充
实例

a = np.array([[1, 2],
              [3, 4]])

b = np.array([[5, 6],
              [7, 8]])

print(np.dot(a,b))


[[19 22]
 [43 50]]

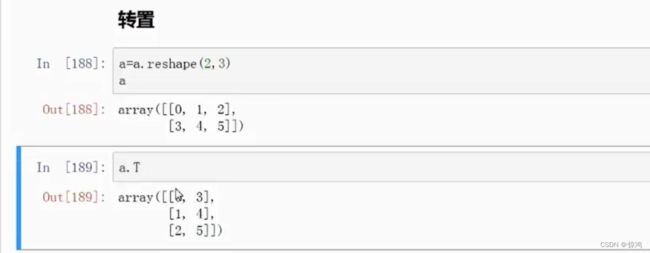
.T：转置矩阵

a = np.array([[1, 2],
              [3, 4]])
print(a.T)

[[1 3]
 [2 4]]

linalg.inv：矩阵求逆

a = np.array([[1, 2],
              [3, 4]])
print(np.linalg.inv(a))


[[-2.   1. ]
 [ 1.5 -0.5]]

三、索引的使用

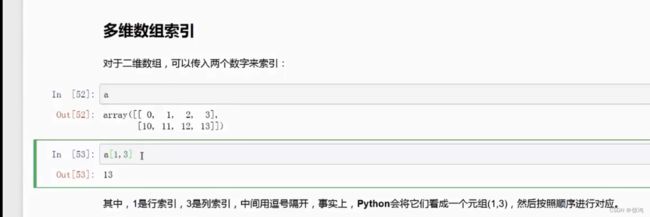
取绝对位置的元素

这他喵的还要我教的话，那你就别学数据结构了，这是最基本的索引，下标知识。

• 下标是从 0 开

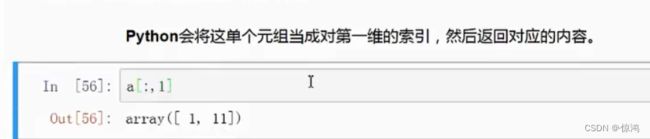
取指定范围元素

这里就简单复习一下切片
这博主写的不错！（书写的不错~）
python之切片

实例

a = np.array([[1, 2, 3, 4],
             [5, 6, 7, 8],
             [9, 10, 11, 12]])

# 冒号表示所取的范围，跟列表的索引用法一样，
# 逗号用来区分每个维度，下面的代码表示[取倒数第二行到最后一行, 第二列到第三列
print(a[-2:, 1:3])

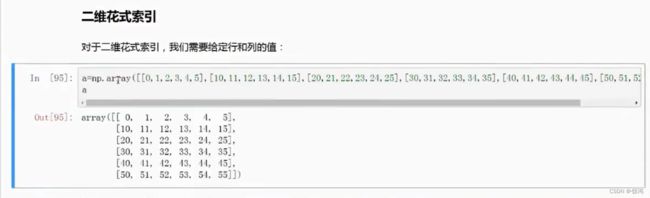
对指定范围元素进行运算

实例

a = np.array([
                [1, 2, 3, 4],
                [5, 6, 7, 8],
                [9, 10, 11, 12]
            ])

a[[0, 1, 2], [1, 1, 1]] += 10
print(a)

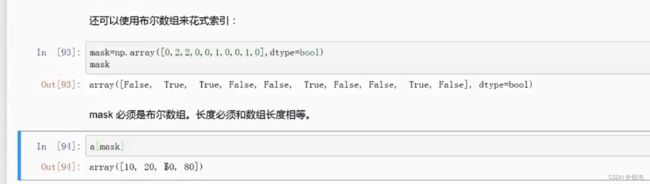
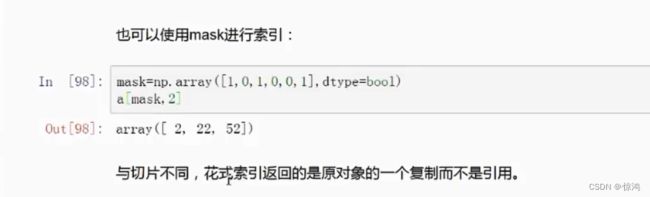
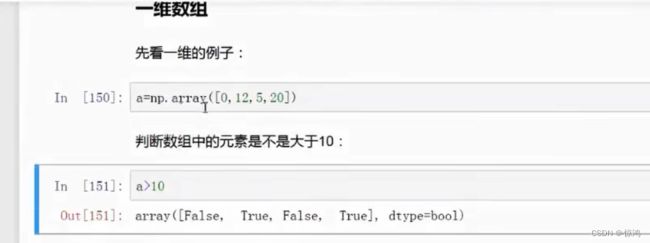
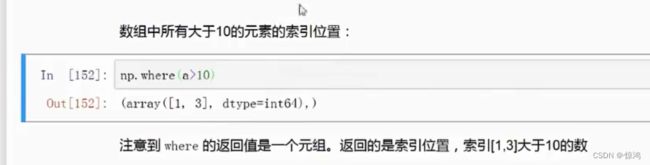
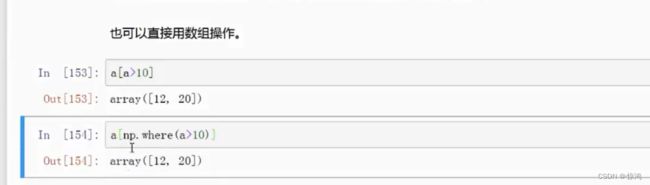
获取数组中大于或小于某个确定值的数值

result_index = a > 10

[[False  True False False]
 [False  True False False]
 [False  True  True  True]]

四、元素数据类型

dtype：查看数据类型

a1 = np.array([1, 2,  3])

print(a1.dtype)


int32

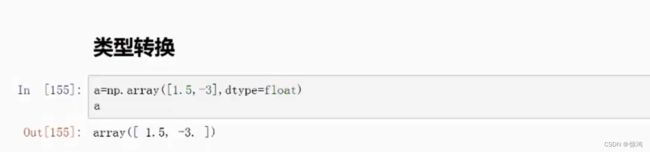
astype：转换数据类型

a = np.array(['1.2', '1.3', '1.4'], dtype = np.string_)

 array([b'1.2', b'1.3', b'1.4'], dtype='|S3')


a.astype(np.float)
array([1.2, 1.3, 1.4])

sry，我看了看比赛的赛题要求，资格赛的pands，numpy，Matplotlib都是考的基础，但是，半决赛要求的大数据我好多都还没学！悲催的我才转行三个月，so，上面的知识我后面比赛完了补充！

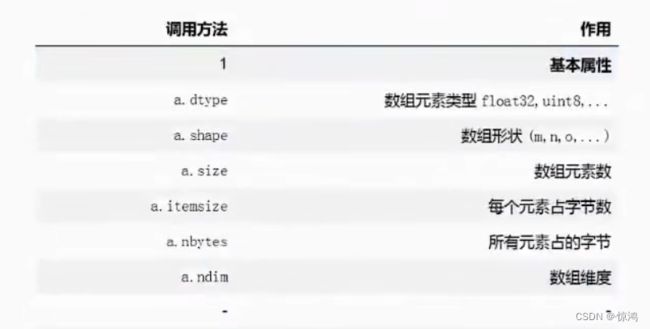
# 查看类型

a= np.linspace(1,10,10)
print(a)
# 查看数据的类型
print(type(a))
# 查看数组中的数据类型 dtype
print(a.dtype)
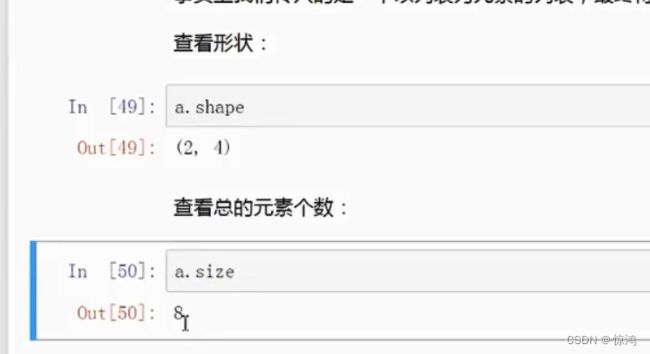
# 查看形状  返回一个元组
print(a.shape)
#查看元素的数目
print(a.size)
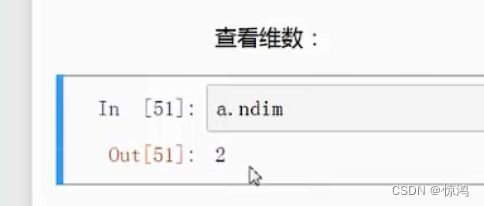
# 查看数组的维度
print(a.ndim)

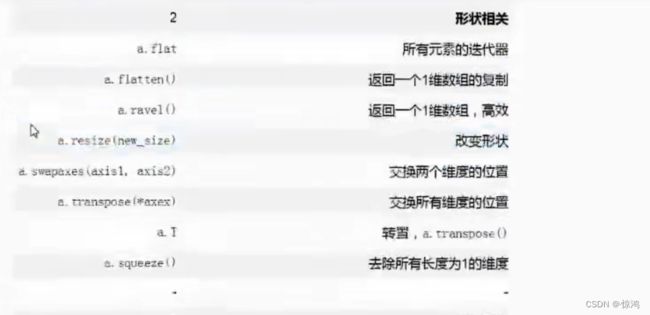
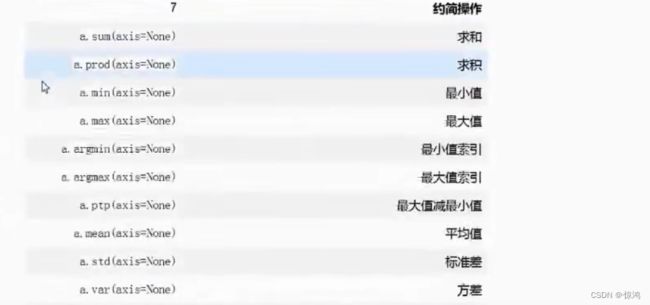
五 、截图

此处优化为

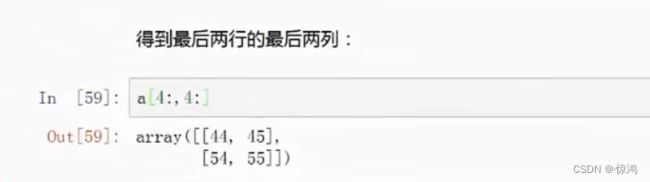
a[-2:,-2:]

更好

---

↑同zip函数概念

以上截图是网上听课，主要是他原视频也这么胡