李宏毅《深度学习》笔记（二）
李宏毅《深度学习》笔记（二）
这篇是关于李宏毅老师《深度学习》视频P3-P4的笔记。李宏毅老师结合宝可梦的例子讲回归，深入浅出，很适合入门学习。
一、 回归介绍
-
回归（Regression ）是监督学习关于连续值最常见的方法，就是找到一个函数 functionfunction ，通过输入特征 xx，输出一个数值 Scalar。例如，股市预测（Stock market forecast）；Pokemon精灵攻击力预测（Combat Power of a pokemon）。
-
结合笔记（一）介绍的建立模型（或者说寻找function）的步骤，建立模型的步骤为：
-
step1：模型假设，选择模型框架（线性模型）
根据输入特征的个数，选择训练模型。如一元线性模型， y = b + w ⋅ x c p y=b+w·x_{cp} y=b+w⋅xcp；或多元线性模型， y = b + ∑ w i ⋅ x i y=b+\sum w_i·x_i y=b+∑wi⋅xi；或一元二次回归模型等
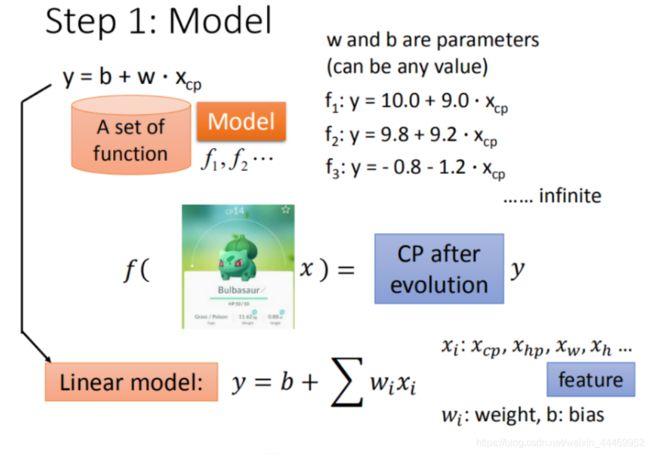
视频中用的就是宝可梦的例子，预测进化后的cp值时，可以使用许多特征：进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）等。
-
step2：模型评估，如何判断众多模型的好坏（损失函数）
衡量模型好坏的方法就是损失函数，即每个数据点通过function得到的预测值与真实值之差的平方和。
-
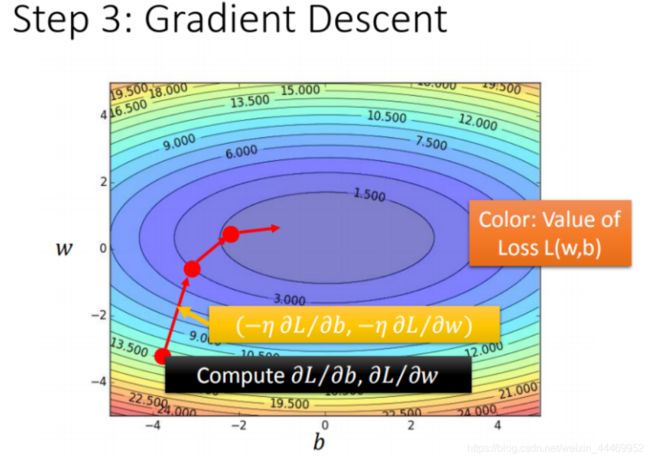
step3：模型优化，如何筛选最优的模型（梯度下降）
得到损失函数后重点在求解得出b和w的值，常见的方法可以有最小二乘法（Ordinary Least Squares）、极大似然估计（Maximum Likelihood Estimate），梯度下降法（Gradient Descent）。视频里主要介绍了梯度下降法。
-
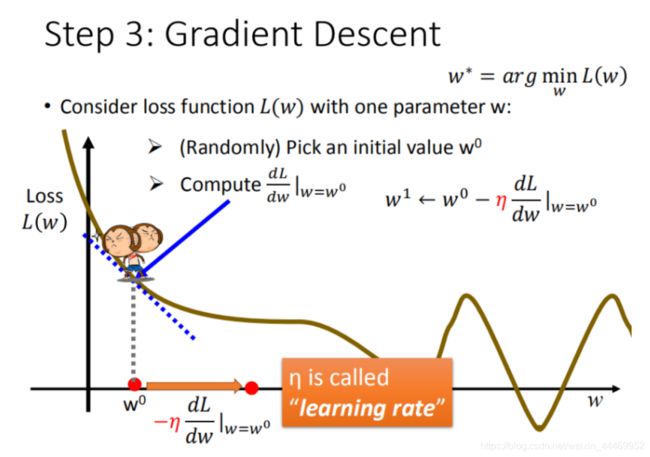
- 步骤1：随机选取一个 w 0 w^0 w0
- 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
- 大于0向右移动（增加w）
- 小于0向左移动（减少w）
- 步骤3：根据学习率移动
- 重复步骤2和步骤3，直到找到最低点
新w和b取值办法如下：
其中，学习率即移动的步长
吴恩达教授介绍关于学习率（Learning Rate）
https://www.youtube.com/watch?v=W0GdZchasxk&list=PLOXON7BTL9IW7Ggbc09jLqGmzkwPI4-3V&index=11
可以将各个w和b计算得到损失函数绘制成图
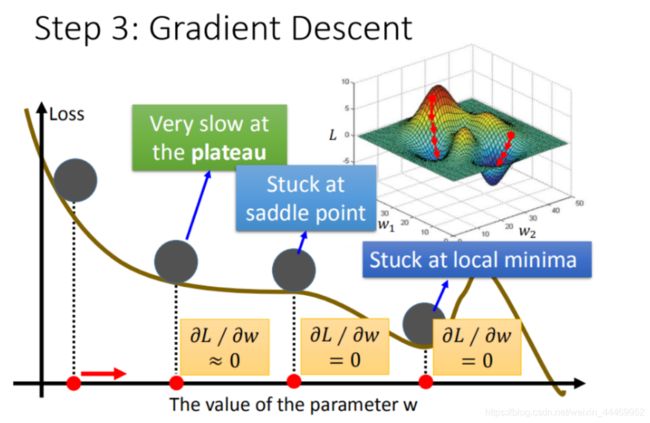
但是在梯度下降过程中，会遇到一些问题：
- 问题1：当前最优（Stuck at local minima）
- 问题2：等于0（Stuck at saddle point）
- 问题3：趋近于0（Very slow at the plateau）
绘制得到的图形可能会如图这般是一个山谷形状，可能在不同的初始点会得到不同的结果，即存在局部最优的情况。在更复杂的算法中，还会出现问题2和问题3。
二、正则化
在模型优化时，增加更多的参数和变量是办法之一。但存在的一个问题就是过拟合，为了解决过拟合问题，我们可以采用正则化的方法。
正则化：正则化是结构风险最小化策略的实现，就是在损失函数（经验风险）上加一个正则化项(Regularizer)或称罚项（Penalty Term）。正则化项，一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。
正则化项可以去不同的形式，主要可以有 L 1 L_1 L1范数: λ 2 ⋅ ∣ ∣ w ∣ ∣ 2 \frac{\lambda}{2}·||w||^2 2λ⋅∣∣w∣∣2以及L_2范数 λ ⋅ ∣ ∣ w ∣ ∣ 1 {\lambda}·||w||_1 λ⋅∣∣w∣∣1
正则化的作用就是选择经验风险与模型复杂度同时比较小的模型
三、回归与梯度下降法的代码实现
现在假设有10个x_data和y_data，x和y之间的关系是y_data=b+w*x_data。b，w都是参数，是需要学习出来的。现在我们来练习用梯度下降找到b和w。
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl # matplotlib没有中文字体，动态解决
plt.rcParams[‘font.sans-serif’] = [‘Simhei’] # 显示中文
mpl.rcParams[‘axes.unicode_minus’] = False # 解决保存图像是负号’-'显示为方块的问题
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
# loss
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
Z[j] [i] = 0 # meshgrid吐出结果：y为行，x为列
for n in range(len(x_data)):
Z[j] [i] += (y_data[n] - b - w * x_data[n]) ** 2
Z[j] [i] /= len(x_data)
先给b和w一个初始值，计算出b和w的偏微分
# linear regression
#b = -120
#w = -4
b=-2
w=0.01
lr = 0.000005
iteration = 1400000
b_history = [b]
w_history = [w]
loss_history = []
import time start = time.time()
for i in range(iteration):
m = float(len(x_d))
y_hat = w * x_d +b
loss = np.dot(y_d - y_hat, y_d - y_hat) / m
grad_b = -2.0 * np.sum(y_d - y_hat) / m
grad_w = -2.0 * np.dot(y_d - y_hat, x_d) / m
#update param
b -= lr * grad_b
w -= lr * grad_w
b_history.append(b)
w_history.append(w)
loss_history.append(loss)
if i % 10000 == 0:
print(“Step %i, w: %0.4f, b: %.4f, Loss: %.4f” % (i, w, b, loss))
end = time.time()
print(“大约需要时间：”,end-start)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap(‘jet’)) # 填充等高线
plt.plot([-188.4], [2.67], ‘x’, ms=12, mew=3, color=“orange”)
plt.plot(b_history, w_history, ‘o-’, ms=3, lw=1.5, color=‘black’)
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r’ b b b’)
plt.ylabel(r’ w w w’)
plt.title(“线性回归”)
plt.show()
为了避免学习率过大或过小，再给b和w特制化两种Learning rate：
# linear regression
b = -120
w = -4
lr = 1
iteration = 100000
b_history = [b]
w_history = [w]
lr_b=0
lr_w=0
import time
start = time.time()
for i in range(iteration):
b_grad=0.0
w_grad=0.0
for n in range(len(x_data)):
b_grad=b_grad-2.0*(y_data[n]-n-w*x_data[n])1.0
w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
lr_b=lr_b+b_grad**2
lr_w=lr_w+w_grad**2
#update param
b -= lr/np.sqrt(lr_b) * b_grad
w -= lr /np.sqrt(lr_w) * w_grad
b_history.append(b)
w_history.append(w)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap(‘jet’)) # 填充等高线
plt.plot([-188.4], [2.67], ‘x’, ms=12, mew=3, color=“orange”)
plt.plot(b_history, w_history, ‘o-’, ms=3, lw=1.5, color=‘black’)
plt.xlim(-200, -100) plt.ylim(-5, 5) plt.xlabel(r’ b b b’)
plt.ylabel(r’ w w w’) plt.title(“线性回归”)
plt.show()