Python--numpy知识点(持续更新)
目录
- 一.ndarray数组
-
- numpy.array()
- 二.numpy.array()的方法
-
- (一)基本属性
-
- 1. .ndim
- 2. .dtype
- (二)numpy.shape和numpy.reshape
-
- 1.numpy.shape(array) / .shape
- 2.numpy.reshape(array, (newshape)) / .reshape(newshape)
- (三)数据和排序
-
- 1.numpy.sum(array,axis,dtype) / .sum(axis,dtype)
- 2.numpy.max(array,axis,dtype) / .max(axis,dtype)
- 3.numpy.min(array,axis,dtype) / .min(axis,dtype)
- 4.numpy.average(array,axis,dtype) / .average(axis,dtype)
- 5.numpy.sort(array,axis,dtype) / .sort(axis,dtype)
- (四)ravel和flatten
-
- 1.numpy.ravel() / .ravel()
- 2. .flatten()
- (五)其他
-
- 1.numpy.transpose() / .transpose() / .T
- 2.numpy.squeeze(array,axis) / .squeeze(array,axis)
- 三.一般函数
-
- (一)产生数组
-
- 1.等差数组
-
- 1.1 numpy.arange(start,end,step)
- 1.2 numpy.linspace(start,stop,num,endpoint,dtype)
- 2.常数数组
-
- 2.1 numpy.ones(shape,dtype)
- 2.2 numpy.zeros(shape,dtype)
- 2.3 numpy.full(shape, fill_value, dtype)
- 3.随机数组numpy.random
-
- 3.1 numpy.random.rand()
- 3.2 numpy.random.random()
- 3.3 numpy.random.randn()
- 3.4 numpy.random.randint(*args) / numpy.random.randint(low,high,size,dtype)
- (二)维度运算
-
- numpy.newaxis
- (三)元素运算
-
- 1.矢量与矢量的常规运算,矢量和标量的运算
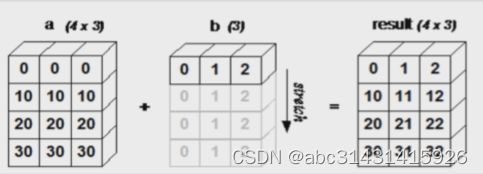
- 2.广播Broadcast
- 3.numpy.all()
- 4.numpy.absolute() / numpy.abs()
- 5.numpy.floor(array,dtype)
- (四)矩阵运算
-
- 1.numpy.dot(array1,array2)
- 2.numpy.rot90(array,num)
- 3.numpy.fliplr(array)
- 4.numpy.meshgrid(array1,array2)
- (五)行列处理
-
- 1.numpy.hsplit(array,indices_or_sections)
- 2.numpy.vsplit(array,indices_or_sections)
- 3.numpy.c_[array1,array2] / numpy.hstack([array1,array2])
- 4.numpy.r_[array1,array2] / numpy.vstack([array1,array2])
- 5.numpy.tile(array,shape)
- (六)视图view与拷贝copy
- 四.文件读取
-
- numpy.genfromtxt(fname, dtype, comments, delimiter, autostrip, skipd_header, skip_fonter, converters, missing_values, filling_values, usecols)
- 五.余弦相似度
- 六.其他
-
- (一)关系操作符可以产生元素为True或False的数组
- (二)标量与数组
-
- numpy.sin(), numpy.cos()
一.ndarray数组
numpy.array()
N维数组对象(矩阵),所有元素必须是相同类型
numpy对象分为数组array和矩阵mat,需要与列表list进行区分
- 二维数组的第一维是列,第二维是行;(3,2)表示在一列上排序第三,一行是排序第二,即第三行第二列
- [0,1,2]可以表示一维矩阵,[[0,1,2]]表示二维矩阵1*3
二.numpy.array()的方法
(一)基本属性
1. .ndim
表示维度个数
2. .dtype
(数据类型对象)属性,表示数据类型
import numpy
data=[[1,2],[3,4],[5,6]]
x=numpy.array(data)
print(x)
#[[1 2],[3 4],[5 6]]
print(x.ndim)
#2
print(x.dtype)
#int32
(二)numpy.shape和numpy.reshape
1.numpy.shape(array) / .shape
用于读取矩阵的长度,表示各维度大小
前者返回值:
- 当参数array为一个数时,返回空元组;
- 为一维矩阵时,返回一个数字的元组;
- 为二维矩阵时,返回行和列组成的元组
后者返回值:看前面的数组array,其他同上,不要“()”
可以认为,一维是最外面的中括号,一维数是最外面中括号内的元素数,二维是第二层,以此类推
import numpy as np
print(np.shape(7))
#()
a=numpy.array([7,8])
print(a.shape)
#(2,)
print(np.shape([[7,8],[1,2],[100,102]]))
#(3, 2)
2.numpy.reshape(array, (newshape)) / .reshape(newshape)
用于在不更改数据的情况下为数组赋予新形状。
参数:
(1)array:需要reshape的数组
(2)newshape:新形状应与原始形状兼容。如果是整数,则结果将是该长度的一维数组。一个形状尺寸可以为-1或其他负数。在这种情况下,该值是根据数组的长度和其余维由系统来推断的。
import numpy as np
a=np.array([[2,3,4],[5,6,7]])
a=np.reshape(a,(3,2))
print(a)
#[[2 3],[4 5],[6 7]]
b=np.array([[2,3,4],[5,6,7]])
b=b.reshape(2,-2)
print(b)
#[[2 3 4],[5 6 7]]
c=b.reshape(-1,2)
print(c)
#[[2 3],[4 5],[6 7]]
说明:
reshape新生成数组和原数组公用一个内存,不管改变哪个都会互相影响
import numpy as np
a=np.array([[1,2],
[3,4]])
b=a.reshape(1,4)
b*=2
print(a)
#[[2 4]
# [6 8]]
print(b)
#[[2 4 6 8]]
可以同时使用arange和reshape创建一个数组
import numpy as np
print(np.arange(1,6).reshape(5,1))
#[[1]
# [2]
# [3]
# [4]
# [5]]
(三)数据和排序
1.numpy.sum(array,axis,dtype) / .sum(axis,dtype)
求和
参数:
(1)array
(2)axis:维度,缺省为-1
(3)dtype
2.numpy.max(array,axis,dtype) / .max(axis,dtype)
求最大值
3.numpy.min(array,axis,dtype) / .min(axis,dtype)
求最小值
4.numpy.average(array,axis,dtype) / .average(axis,dtype)
求平均值
5.numpy.sort(array,axis,dtype) / .sort(axis,dtype)
排序
import numpy as np
vector1=np.array([26,10,15,20])
print(vector1.sum())
#71
print(vector1.max())
#26
print(vector1.min())
#10
print(np.average(vector1))
#17.75
print(np.sort(vector1))
#[10 15 20 26]
vector2=np.array([[35,5,15],
[10,25,45],
[20,40,30]])
print(vector2)
#[[35 5 15],[10 25 45],[20 40 30]]
print(vector2.max(axis=0))#第一维列取最大值
#[35 40 45]
print(vector2.max(axis=1))#第二维行取最大值
#[35 45 40]
print(vector2.sum(axis=0))#第一维列求和
#[65 70 90]
print(vector2.sum(axis=1))#第二维行求和
#[55 80 90]
(四)ravel和flatten
1.numpy.ravel() / .ravel()
将多维数组转换为一维
返回值:视图(view),会影响原始矩阵
2. .flatten()
将多维数组转换为一维
返回值:拷贝(copy),对拷贝所做的修改不会影响原始矩阵
说明:
- 只能适用于numpy对象,即array或者mat,普通的list列表是不行的
- 没有函数numpy.flatten()
import numpy as np
a = np.array([[1, 2],[3, 4]])
b=a.flatten()
b*=2
print(a)
#[[1 2],[3 4]]
print(b)
#[2 4 6 8]
c1=a.ravel()
c2=np.ravel(a)
c1*=2
print(a)
#[[2 4],[6 8]]
print(c1)
#[2 4 6 8]
print(c2)
#[2 4 6 8]
#降维默认行序有限,传入参数‘F’表示列序优先
d=a.ravel('F')
print(d)
#[2 6 4 8]
(五)其他
1.numpy.transpose() / .transpose() / .T
矩阵转置
import numpy as np
x1=np.array([[90,10,15],[20,25,30]])
x2=np.array([[5,10,15],[20,25,30],[90,10,15],[90,10,15]])
x1_x2_1=np.dot(x1,x2.transpose())
x1_x2_2=np.dot(x1,np.transpose(x2))
print(x1_x2_1)
#[[ 775 2500 8425 8425],[ 800 1925 2500 2500]]
print(x1_x2_2)
#[[ 775 2500 8425 8425],[ 800 1925 2500 2500]]
2.numpy.squeeze(array,axis) / .squeeze(array,axis)
从数组的形状中删除单维度条目,即把shape中为1的维度去掉
返回值:维度可能减少的数组
参数:
(1)array:输入的数组
(2)axis:指定需要删除的维度,但是指定的维度必须为单维度,否则将会报错;取值可为None或int或tuple of ints,可选。若axis为空,则删除所有单维度的条目
- 此函数不会修改原数组
- 在机器学习和深度学习中,通常算法的结果是可以表示向量的数组(即包含两对或以上的方括号形式[[]]),如果直接利用这个数组进行画图可能显示界面为空。可以利用squeeze()函数将表示向量的数组转换为秩为1的数组
import numpy as np
a=np.array([[1,2,3]])
b=np.squeeze(a)
c=a.squeeze()
print(b)
#[1 2 3]
print(c)
#[1 2 3]
三.一般函数
(一)产生数组
1.等差数组
1.1 numpy.arange(start,end,step)
参数:
(1)start:数值范围的起始点
(2)end:数值范围的终止点,不包括此值
(3)step:数值范围的步长
import numpy as np
print(np.arange(6))
#[0 1 2 3 4 5]
print(np.arange(0,6,2))
#[0 2 4]
print(np.arange(0,6,0.9))
#[0. 0.9 1.8 2.7 3.6 4.5 5.4]
1.2 numpy.linspace(start,stop,num,endpoint,dtype)
参数:
(1)start:数值范围的起始点
(2)stop:数值范围的终止点
(3)num(可选):结果中的元素数,缺省为50
(4)endpoint(可选):决定终止值是否被包含在结果数组中,若endpoint=True,结果中包括终止值,反之不包括,缺省为True
(5)dtype(可选):决定输出数组的数据类型
说明:
| numpy.linspace(start=0,stop=100,num=5) | numpy.linspace(0,100,5) |
|---|---|
| 命名参数 | 位置参数 |
两者差别:
- 前者区间左闭右开,后者区间在endpoint=True左闭右闭,在endpoint=False左闭右开
- 当steps和num指定参数都是整数,arange会返回numpy.int32数据类型,而linspace会返回numpy.float数据类型
import numpy as np
a=np.arange(0,10,step=1)
b=np.arange(0,10,step=1.0)
c=np.linspace(0,10,num=10,endpoint=False)
d=np.linspace(0,10,num=11,endpoint=True)
print(a)
#[0 1 2 3 4 5 6 7 8 9]
print(b)
#[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
print(c)
#[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
print(d)
#[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
2.常数数组
2.1 numpy.ones(shape,dtype)
生成全1矩阵
参数:
(1)shape:可以是数也可以是元组,表示数组的形状
(2)dtype
import numpy as np
a=np.ones(4)
b=np.ones((2,3,4),dtype=np.int32)
print(a)
#[1. 1. 1. 1.]
print(b)
#[[[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]
# [[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]]
2.2 numpy.zeros(shape,dtype)
生成全0矩阵
参数:
(1)shape:可以是数也可以是元组,表示数组的形状
(2)dtype
import numpy as np
a=np.zeros(5)
b=np.zeros((3,4))
print(a)
#[0. 0. 0. 0. 0.]
print(b)
#[[0. 0. 0. 0.]
# [0. 0. 0. 0.]
# [0. 0. 0. 0.]]
2.3 numpy.full(shape, fill_value, dtype)
生成全是同一个元素的矩阵
参数:
(1)shape:可以是数也可以是元组,表示数组的形状
(2)fill_value:填满的值
import numpy as np
a=np.full(2,3)
b=np.full((2,3),4)
print(a)
#[3 3]
print(b)
#[[4 4 4],[4 4 4]]
3.随机数组numpy.random
numpy.random.seed(int)
随机数种子
以下函数的返回值:
- 当函数括号内没有参数时,则返回一个浮点数或整数
- 当函数括号内有一个参数时,则返回秩为1的一维数组,不能表示向量和矩阵
- 当函数括号内有两个及以上参数时,则返回对应维度的数组,能表示向量或矩阵
3.1 numpy.random.rand()
生成在[0,1)区间服从均匀分布的随机小数
import numpy as np
np.random.seed(2)
a=np.random.rand()
b=np.random.rand(2)
c=np.random.rand(2,3)
print(a)
#0.43599490214200376
print(b)
#[0.02592623 0.54966248]
print(c)
#[[0.43532239 0.4203678 0.33033482]
# [0.20464863 0.61927097 0.29965467]]
3.2 numpy.random.random()
生成在[0,1)区间的随机小数
import numpy as np
np.random.seed(1)
a=np.random.random()
b=np.random.random(2)
c=np.random.random((2,3)) #两个参数以上需要元组形式
print(a)
#0.417022004702574
print(b)
#[7.20324493e-01 1.14374817e-04]
print(c)
#[[0.30233257 0.14675589 0.09233859]
# [0.18626021 0.34556073 0.39676747]]
numpy.random.rand()和numpy.random.random()在使用同样的随机数种子时,似乎会产生同样的随机数,其他函数没有这种情况
3.3 numpy.random.randn()
生成服从(0,1)正态分布的小数
import numpy as np
np.random.seed(1)
a=np.random.randn()
b=np.random.randn(2)
c=np.random.randn(2,3)
d=4*np.random.randn(3,3,3) + 3 #生成服从均值为3,标准差为4的正态分布的三维数组
print(a)
#1.6243453636632417
print(b)
#[-0.61175641 -0.52817175]
print(c)
#[[-1.07296862 0.86540763 -2.3015387 ]
# [ 1.74481176 -0.7612069 0.3190391 ]]
print(d) #三维数组
#[[[ 2.0025185 8.84843175 -5.24056284]
# [ 1.71033118 1.46378258 7.53507777]
# [-1.39956507 2.31028717 -0.51143367]]
# [[ 3.16885499 5.33126085 -1.40247671]
# [ 7.57889484 6.60636288 5.00997736]
# [ 6.6034238 0.26508856 2.5084391 ]]
# [[-0.74307774 1.92844768 5.12142187]
# [ 0.23335699 1.41298589 0.2513092 ]
# [-0.38082257 0.31501548 2.9493416 ]]]
3.4 numpy.random.randint(*args) / numpy.random.randint(low,high,size,dtype)
生成在一定区间的整数,至少要有一个参数
参数:
(1)*args:三个数字,用于分别对应low,high,size
(2)low(可选):int or float,生成的数值的最小值(包含),缺省为0
(3)high:int or float,生成的数值的最大值(不包含)
(4)size(可选):int or tuple of ints,随机数的尺寸,整数表示生成的数量,元组表示数组的形状,缺省为1,空元组视为1
(5)dtype(可选):输出的结果类型,缺省为int
import numpy as np
np.random.seed(1)
a=np.random.randint(10) #0到10的一个随机整数
b=np.random.randint(1,10) #1到10的一个随机整数
c=np.random.randint(1,10,10) #1到10的十个随机整数,构成一维数组
d=np.random.randint(10,99,(5,5)) #10到99的二十五个随机整数,构成5*5的二维数组
print(a)
#5
print(b)
#9
print(c)
#[6 1 1 2 8 7 3 5 6 3]
print(d)
#[[94 21 38 39 24]
# [60 78 97 97 96]
# [23 19 17 73 71]
# [32 67 11 10 70]
# [91 18 98 23 57]]
特殊用法:
import numpy as np
np.random.seed(1)
# 可单独指定每个元素的最小值和最大值
# 如果不指定 size 默认根据第一个和第二个参数的长度来决定生成结果的长度
a=np.random.randint([3, 5, 7], 10) #生成3个分别不小于3,5,7的值,都小于10的值
print(a)
#[8 8 7]
b=np.random.randint(1, [3, 5, 10]) #生成3个都不小于1,分别小于3,5,10的值
print(b)
#[1 4 6]
c=np.random.randint([1, 2, 3,], [4, 5, 10]) #生成3个分别不小于1,2,3,分别小于4,5,10的值
print(c)
#[1 2 4]
#生成2*4的数组,其中每一行不小于[1, 3, 5, 7],第一行都小于10,第二行都小于20
#注意第二个参数里面的每个元素都要用[],因为它控制的是一整行
d=np.random.randint([1, 3, 5, 7], [[10], [20]])
print(d)
#[[ 8 8 9 9]
# [19 8 7 11]]
#生成4*2的数组,其中,第一行都不小于1,第二行都不小于3,第三行都不小于5,第四行都不小于7,每一行都小于[10,20]
e=np.random.randint([[1],[3],[5],[7]],[10,20])
print(e)
#[[ 3 5]
# [ 4 3]
# [ 6 14]
# [ 8 13]]
当产生二维以上的数组时,numpy.random.rand()和numpy.random.randn()只需要一个小括号(),而numpy.random.random()和numpy.random.randint()需要两个小括号()
(二)维度运算
numpy.newaxis
插入新维度
y=x[:,np.newaxis]效果相当于在最里层中括号内的元素加上一个中括号,y=x[np.newaxis,:]效果相当于在最外层加上一个中括号
import numpy as np
x1=np.arange(3)
print(np.shape(x1))
#(3,)
x2=x1[:,np.newaxis]
print(x2)
#[[0],[1],[2]]
print(np.shape(x2))
#(3, 1)
x3=x1[np.newaxis,:]
print(x3)
#[[0 1 2]]
print(np.shape(x3))
#(1, 3)
vector1=np.array([5,10,15,20])
print(vector1[0:3])
#[ 5 10 15]
vector2=np.array([[5,10,15],[20,25,30],[35,40,45]])
print(vector2[:,1])
#[10 25 40]
print(vector2[:,0:2])
#[[ 5 10],[20 25],[35 40]]
print(vector2[1:3,0:2])
#[[20 25],[35 40]]
(三)元素运算
1.矢量与矢量的常规运算,矢量和标量的运算
前者,形状大小相同的数组键间的运算应用在元素上,对应元素相加减乘除
后者,标量运算应用在每一个元素上
| 对应元素相乘 | 对应元素相除 |
|---|---|
| array1*array2 | array1/array2 |
| numpy.multiply(array1,array2) | numpy.divide(array1,array2) |
import numpy as np
a=np.array([1,2])
b=np.array([3,4])
c1=b+a
c2=b-a
c3=b*a
c4=b/a
d=a*2+b*3
print(c1)
#[4 6]
print(c2)
#[2 2]
print(c3)
#[3 8]
print(c4)
#[3. 2.]
print(d)
#[11 16]
vector1=numpy.array([[2,6,3],[2,1,2]])
vector2=numpy.array([[1,2,3],[4,5,8]])
m1=vector1*vector2
m2=numpy.multiply(vector1,vector2)
print(m1)
#[[ 2 12 9],[ 8 5 16]]
print(m2)
#[[ 2 12 9],[ 8 5 16]]
n1=vector1/vector2
n2=numpy.divide(vector1,vector2)
print(n1)
#[[2. 3. 1. ],[0.5 0.2 0.25]]
print(n2)
#[[2. 3. 1. ],[0.5 0.2 0.25]]
2.广播Broadcast
import numpy as np
a=np.array([[1,2],[2,6]])
b1=np.array([1,2])
b2=np.array([[1,2]])
b3=np.array([[[1,2]]])
print(a+b1)
#[[2 4],[3 8]]
print(a+b2)
#[[2 4],[3 8]]
print(a+b3)
#[[[2 4],[3 8]]]
print(a*b1)
#[[ 1 4],[ 2 12]]
3.numpy.all()
判断整个数组中的元素的值是否全部满足条件
返回值:如果全部满足条件返回True,否则返回False。
4.numpy.absolute() / numpy.abs()
对数组中的每一个元素求其绝对值
import numpy as np
a=np.array([4,2,3])
b=np.array([1,6,9])
c=b-a
print(c)
#[-3 4 6]
d=np.absolute(c)
print(d)
#[3 4 6]
if numpy.all((d)>1):
print('yes')
#yes
5.numpy.floor(array,dtype)
对array中每个元素向下取整
import numpy as np
a=np.array([-1.5,-0.5,0.5,1.5])
b=np.floor(a)
print(b)
#[-2. -1. 0. 1.]
(四)矩阵运算
1.numpy.dot(array1,array2)
矩阵乘法
import numpy as np
vector1=np.array([1,2,3]) #1-D array
vector2=np.array([4,5,6])
m=np.dot(vector1,vector2) #一维矩阵计算两者的内积
print(m)
#32
vector3=np.array([[1,2,3],[4,5,6]]) #2-D array
vector4=np.array([[1,2],[3,4],[5,6]])
n=np.dot(vector3,vector4) #计算两个二维矩阵的乘积
print(n)
#[[22 28],[49 64]]
2.numpy.rot90(array,num)
实现矩阵90°角任意倍数的旋转,正数为逆时针,负数为顺时针
import numpy as np
a=np.array([[1,2],
[3,4]])
b1=np.rot90(a,-1)
b2=np.rot90(a,2)
print(b1)
#[[3 1]
# [4 2]]
print(b2)
#[[4 3]
# [2 1]]
3.numpy.fliplr(array)
矩阵水平镜像翻转
import numpy as np
a=np.array([[1,2],
[3,4]])
b=np.fliplr(a)
print(b)
#[[2 1]
# [4 3]]
4.numpy.meshgrid(array1,array2)
根据平面点的坐标数组生成坐标矩阵
返回值:一个二元素列表
列表元素分别是点x坐标组成的数组和y坐标组成的数组,该数组有几个元素即代表点有几个
import numpy as np
x=np.linspace(1,3,3)
y=np.linspace(4,5,2)
Z=np.meshgrid(x,y)
print(Z)
#[array([[1., 2., 3.],
# [1., 2., 3.]]),
# array([[4., 4., 4.],
# [5., 5., 5.]])]
X,Y=np.meshgrid(x,y)
print(X)
#[[1. 2. 3.],
# [1. 2. 3.]]
print(Y)
#[[4. 4. 4.],
# [5. 5. 5.]]
(五)行列处理
1.numpy.hsplit(array,indices_or_sections)
横着切割数组
参数:
(1)array:被处理的数组
(2)indices_or_sections:索引或节。若为列表,则以列表的元素为索引进行切割;若为正整数,则进行均分,但这个正整数必须能被整除
2.numpy.vsplit(array,indices_or_sections)
竖着切割数组,同上
import numpy as np
np.random.seed(10)
a1=np.floor(10*np.random.random((2,6))) #random会产生0-1的随机数
a2=np.floor(10*np.random.random((6,2))) #a1,a2的元素都是0-9的整型浮点数
print(a1)
#[[7. 0. 6. 7. 4. 2.],
# [1. 7. 1. 0. 6. 9.]]
print(a2)
#[[0. 5.],
# [8. 6.],
# [7. 2.],
# [9. 7.],
# [5. 1.],
# [3. 6.]]
b=np.hsplit(a1,3)
print(b)
#[array([[7., 0.],
# [1., 7.]]),
# array([[6., 7.],
# [1., 0.]]),
# array([[4., 2.],
# [6., 9.]])]
b1,b2,b3=np.hsplit(a1,3)
print(b1)
#[[7. 0.]
# [1. 7.]]
print(b2)
#[[6. 7.]
# [1. 0.]]
print(b3)
#[[4. 2.]
# [6. 9.]]
c=np.vsplit(a2,[1,3,5])
print(c)
#[array([[0., 5.]]),
# array([[8., 6.],
# [7., 2.]]),
# array([[9., 7.],
# [5., 1.]]),
# array([[3., 6.]])]
c1,c2,c3,c4=np.vsplit(a2,[1,3,5])
print(c1)
#[[0. 5.]]
print(c2)
#[[8. 6.]
# [7. 2.]]
print(c3)
#[[9. 7.]
# [5. 1.]]
print(c4)
#[[3. 6.]]
3.numpy.c_[array1,array2] / numpy.hstack([array1,array2])
沿左右的方向顺序横着拼接,行数必须相等
4.numpy.r_[array1,array2] / numpy.vstack([array1,array2])
沿上下的方向顺序竖着拼接,列数必须相等
import numpy as np
a=np.arange(1,5).reshape(4,1)
b=np.ones((4,2))
c=np.hstack((a,b))
d=np.c_[a,b]
print(c)
#[[1. 1. 1.]
# [2. 1. 1.]
# [3. 1. 1.]
# [4. 1. 1.]]
print(d)
#[[1. 1. 1.]
# [2. 1. 1.]
# [3. 1. 1.]
# [4. 1. 1.]]
5.numpy.tile(array,shape)
把数组沿各个方向复制
参数:
(1)array
(2)shape:元组,维度必须与array一致,元素均为整数
import numpy as np
a=np.array([[1,2],
[3,4]])
b=np.tile(a,(2,3))
print(b)
#[[1 2 1 2 1 2]
# [3 4 3 4 3 4]
# [1 2 1 2 1 2]
# [3 4 3 4 3 4]]
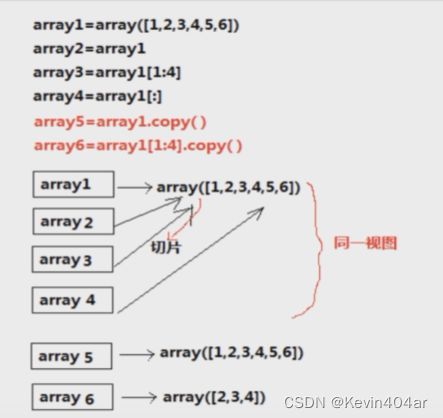
(六)视图view与拷贝copy
- b=a:与源数组完全相同,id相同,其任何修改都会影响源数组
- c=a[:],d=a.view():数组切片是原始数组的视图view,视图上的任何修改都会影响源数组
- e=a.copy():拷贝copy,修改不会影响源数组
import numpy as np
a=np.arange(4)
print(a)
#[0 1 2 3]
b=a
print(b)
#[0 1 2 3]
print(b is a)
#True
print(id(a))
#2522915940944
print(id(b))
#2522915940944
b*=2
print(id(a))
#2522915940944
print(id(b))
#2522915940944
print(a)
#[0 2 4 6]
print(b)
#[0 2 4 6]
c=a[:]
print(c)
#[0 2 4 6]
print(c is a)
#False
print(id(a))
#2522915940944
print(id(c))
#2522915942000
c*=2
print(a)
#[ 0 4 8 12]
print(c)
#[ 0 4 8 12]
d=a.view()
print(d)
#[ 0 4 8 12]
print(d is a)
#False
print(id(a))
#2522915940944
print(id(d))
#2522915941136
d*=2
print(a)
#[ 0 8 16 24]
print(d)
#[ 0 8 16 24]
e=a.copy()
print(e)
#[ 0 8 16 24]
print(e is a)
#False
print(id(a))
#2522915940944
print(id(e))
#2522915796048
e*=2
print(a)
#[ 0 8 16 24]
print(e)
#[ 0 16 32 48]
四.文件读取
numpy.genfromtxt(fname, dtype, comments, delimiter, autostrip, skipd_header, skip_fonter, converters, missing_values, filling_values, usecols)
默认是按照float格式来读取的,对于不能转换为float类型的数据会读取为nan(not a number),故应加入参数
参数:
(1)fname:str/list/IO Object等等,表示数据源;文件路径,字符串列表、StringIO对象都可;若以gz结尾,读取时会在加载数据之前自动解压,但较为常见的都是txt文本
IO --> input,output
(2)dtype:dtype,最终数组的数据类型
(3)comments:str,注释标识符,加载时会自动忽略位于注释标识符所在行后面的字符串;
(4)delimiter:str/int/sequence
- 若delimiter为字符,表示分割符,每一行的元素以分割符进行分割;
- 若delimiter为字符列表,表示分割符可为多个字符;
- 若delimiter为整数元组时,代表每一列所在元素最大宽度
import numpy as np
from io import BytesIO
data1 = b"1, 2, 3\n4, 5, 6"
a=np.genfromtxt(BytesIO(data1), delimiter=",")
print(a)
#[[1. 2. 3.]
# [4. 5. 6.]]
data2 = b" 1 2 3\n 4 5 67\n890123 4"
b=np.genfromtxt(BytesIO(data2), delimiter=3)
print(b)
#[[ 1. 2. 3.]
# [ 4. 5. 67.]
# [890. 123. 4.]]
data3 = B"123456789\n 4 7 9\n 4567 9"
c=np.genfromtxt(BytesIO(data3), delimiter=(4, 3, 2))
print(c)
#[[1234. 567. 89.]
# [ 4. 7. 9.]
# [ 4. 567. 9.]]
(5)autostrip:若为True,元素中的空格标识符会被自动删除
(6)skip_header:int,数据加载时跳过文件头部的字符串行数
(7)skip_footer:int,数据加载时跳过文件尾部的字符串行数
(8)converters:variable,可以是字典形式也可以是lambda函数,表示将某一种数据格式转化为另一种数据格式
(9)missing_values:variable,指定数组中的缺失值进行标记
(10)filling_values:variable,指定数组中已标记的缺失值,来替代填充值
举例:
missing_values={0:“N/A”, 1:" “, 2:”???"}, filling_values={0:0,1:0, 2:-999})
(11)usercols:sequence,指定只读取数据中指定的列数, 0表示第一列,-1为最后一列
五.余弦相似度
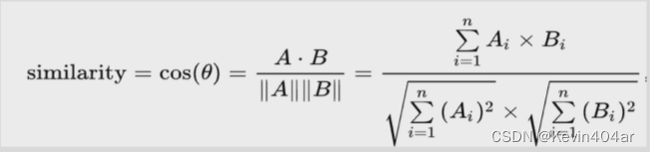
||A||表示A的范数,用numpy.linalg.norm()表示,可利用axis实现降维计算
import numpy as np
v1=np.array([1,2,3])
v2=np.array([7,14,5])
result=(np.sum(v1*v2))/(np.linalg.norm(v1)*np.linalg.norm(v2))
print(result)
#0.8132500607904444
以下为计算两个矩阵的余弦相似度:
import numpy
matrix1=numpy.array([[90,10,15],
[20,25,30]]) #二维数组2*3
matrix2=numpy.array([[5,10,15],
[20,25,30],
[90,10,15],
[90,10,15]]) #二维数组3*4
matrix1_matrix2=numpy.dot(matrix1,matrix2.T) #计算矩阵乘积,结果为二维数组2*4
matrix1_norm1=numpy.linalg.norm(matrix1,axis=1) #按行取范数,得一维数组1*2
matrix1_norm2=matrix1_norm1[:,numpy.newaxis] #增加维度,变成二维数组2*1
matrix2_norm1=numpy.linalg.norm(matrix2,axis=1) #按行取范数,得一维数组1*4
matrix2_norm2=matrix2_norm1[numpy.newaxis,:] #增加维度,变成二维数组1*4
#余弦相似度
cosine=numpy.divide(matrix1_matrix2,numpy.dot(matrix1_norm2,matrix2_norm2))
print(cosine)
#[[0.45131807 0.62078282 1. 1. ]
# [0.97463185 1. 0.62078282 0.62078282]]
六.其他
(一)关系操作符可以产生元素为True或False的数组
import numpy as np
a=np.array([1,2,3])
print(a>2)
#[False False True]
b=np.array([3,4,5])
print(a<b)
#[ True True True]
x = np.linspace(-2,2,5)
y = np.linspace(0,4,5)
xx,yy = np.meshgrid(x,y)
z = np.square(xx) - yy>0
print(z)
#[[ True True False True True]
# [ True False False False True]
# [ True False False False True]
# [ True False False False True]
# [False False False False False]]
vector=numpy.array([[5,10,15],[20,25,30],[35,40,45]])
vector==25
#array([[False, False, False],
# [False, True, False],
# [False, False, False]])
(二)标量与数组
numpy.sin(), numpy.cos()
import numpy as np
a1=1
a2=np.sin(a1)
print(a2)
#0.8414709848078965
b1=[1,2]
b2=np.sin(b1)
print(b2)
#[0.84147098 0.90929743]
c1=[[1,2],
[3,4]]
c2=np.cos(c1)
print(c2)
#[[ 0.54030231 -0.41614684]
# [-0.9899925 -0.65364362]]
以上未完待更新,仅供个人学习,侵权联系删除,如有错误或不足之处可指出,以便改进。