【数据结构】我家三岁表弟都明白的栈和队列,你不会不了解吧?
作者: @情话0.0
专栏:《数据结构》
个人简介:一名双非编程菜鸟,在这里分享自己的编程学习笔记,欢迎大家的指正与点赞,谢谢!
栈和队列
- 一、栈
-
- 1.栈的基本概念
- 2.栈的顺序存储(数组实现)
-
- 栈的顺序存储类型描述如下:
- 2.1 栈的初始化
- 2.2 检查栈满
- 2.3 入栈:尾插
- 2.4 出栈:尾删
- 2.5 获取栈顶元素
- 2.6 获取栈中有效元素的个数
- 2.7 检测栈是否为空
- 2.8 销毁栈
- 3. 源代码
-
- 3.1 stack.h
- 3.2 stack.c
- 3.3 test.c
- 二、队列
-
- 1.队列的基本概念
- 2.队列的链式存储
-
- 队列的链式存储类型描述如下:
- 2.1 队列初始化
- 2.2 入队
- 2.3 出队
- 2.4 获取队头元素
- 2.5 获取队尾元素
- 2.6 获取队列中有效元素的个数
- 2.7 检测队列是否为空
- 2.8 销毁队列
- 3. 源代码
-
- 3.1 queue.h
- 3.2 queue.c
- 3.3 test.c
- 队列扩展:循环队列
- 总结
一、栈
1.栈的基本概念
栈是只允许在一端进行插入或删除操作的线性表。首先栈是一种线性表,但是对其限定该线性表只能在某一端进行插入或删除操作。
栈顶:进行数据插入和删除操作的一端;
栈底:不允许进行插入和删除的另一端;
空栈:不含任何元素的空表。
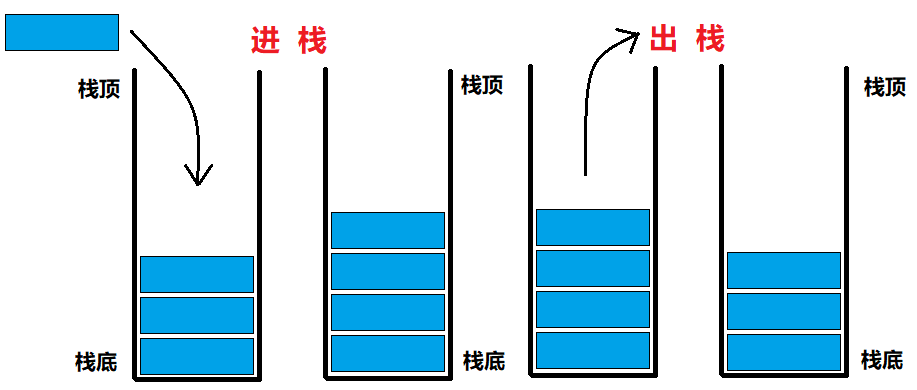
栈中的元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
2.栈的顺序存储(数组实现)
栈是一种操作受限的线性表,可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元(数组)存放自栈底到栈顶的数据元素,同时附设一个指针(top)指示当前栈顶元素的位置。
栈的顺序存储类型描述如下:
typedef int SDataType;
typedef struct Stack
{
SDataType* array;
int capacity; //栈的容量
int top; //栈的元素个数
}Stack;
2.1 栈的初始化
void StackInit(Stack* ps)
{
assert(ps);
ps->array = (SDataType*)malloc(sizeof(SDataType)* 5);
ps->capacity = 5;
ps->top = 0;
}
栈顶指针:ps->top,初始化设置ps->top=0,指向栈顶元素的上层存储单元。
2.2 检查栈满
void CheckCapacity(Stack* ps)
{
assert(ps);
if (ps->top == ps->capacity)
{
SDataType* arr = (SDataType*)realloc(ps->array, sizeof(SDataType)* (ps->capacity)*2);
if (arr == NULL)
{
return;
}
ps->array = arr;
ps->capacity *= 2;
}
}
栈满条件为ps->top == ps->capacity,若空间已满,就进行2倍扩容。
2.3 入栈:尾插
void StackPush(Stack* ps, SDataType data)
{
assert(ps);
CheckCapacity(ps);
ps->array[ps->top++] = data;
}
进栈操作:栈不满时,先将数据存储到top指针指向的存储空间,再将top指针加 1 ;栈满时先扩容,在插入元素。
2.4 出栈:尾删
void StackPop(Stack* ps)
{
assert(!StackEmpty(ps));
ps->top--;
}
出栈操作:先对栈进行断言判断是否为空,非空时只需将top指针减 1 即可,因为下一次进栈直接会将已经出栈的元素覆盖掉。
2.5 获取栈顶元素
SDataType StackTop(Stack* ps)
{
assert(!StackEmpty(ps));
return ps->array[ps->top - 1];
}
2.6 获取栈中有效元素的个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}
由于使用数组来实现,所以栈顶指针的数据和有效元素个数相等。
2.7 检测栈是否为空
int StackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
2.8 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->array);
ps->capacity = 0;
ps->top = 0;
ps->array = NULL;
}
注意:这里的top指针指向栈顶元素的上层存储空间,所以进栈操作为ps->array[ps->top++] = data,出栈操作为ps->top--,。若栈顶指针初始化为ps->top=-1,即top指向栈顶元素,则入栈操作为ps->array[++ps->top]=data,出栈操作不变。栈空判断条件为ps->top==-1,栈满判断条件为++ps->top==ps->capacity。
3. 源代码
3.1 stack.h
#include 3.2 stack.c
#include "stack.h"
void StackInit(Stack* ps)
{
assert(ps);
ps->array = (SDataType*)malloc(sizeof(SDataType)* 5);
ps->capacity = 5;
ps->top = 0;
}
void CheckCapacity(Stack* ps)
{
assert(ps);
if (ps->top == ps->capacity)
{
SDataType* arr = (SDataType*)realloc(ps->array, sizeof(SDataType)* (ps->capacity)*2);
if (arr == NULL)
{
return;
}
ps->array = arr;
ps->capacity *= 2;
}
}
// 入栈:尾插
void StackPush(Stack* ps, SDataType data)
{
assert(ps);
CheckCapacity(ps);
ps->array[ps->top++] = data;
}
// 出栈:尾删
void StackPop(Stack* ps)
{
assert(!StackEmpty(ps));
ps->top--;
}
// 获取栈顶元素
SDataType StackTop(Stack* ps)
{
assert(!StackEmpty(ps));
return ps->array[ps->top - 1];
}
// 获取栈中有效元素的个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}
// 检测栈是否为空
int StackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->array);
ps->capacity = 0;
ps->top = 0;
ps->array = NULL;
}
void Print(Stack* ps)
{
assert(ps);
int i = 0;
while (i < ps->top)
{
printf("%d ", ps->array[i]);
i++;
}
printf("\n");
}
void test()
{
Stack ps;
StackInit(&ps);
StackPush(&ps, 0);
StackPush(&ps, 1);
StackPush(&ps, 2);
StackPush(&ps, 3);
StackPush(&ps, 4);
StackPush(&ps, 5);
Print(&ps);
StackPop(&ps);
Print(&ps);
int ret = StackTop(&ps);
printf("%d\n", ret);
ret = StackSize(&ps);
printf("%d\n", ret);
}
3.3 test.c
#include "stack.h"
int main()
{
test();
return 0;
}
二、队列
1.队列的基本概念
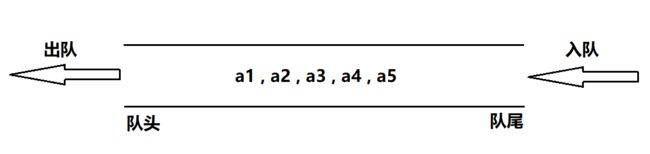
队列也是一种操作受限的线性表,只允许在表的一端进行插入,而在表的另一端进行删除。向队列中插入元素称为入队;删除元素称为出队。
队头:允许删除的一端,又称队首;
队尾:允许插入的一端;
空队列:不含任何元素的空表。
队列中的元素遵守后进先出FIFO(First In First Out)的原则。
2.队列的链式存储
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
队列的链式表示称为链队列,它实际上是一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点,尾指针指向队尾结点,即单链表的最后一个结点。
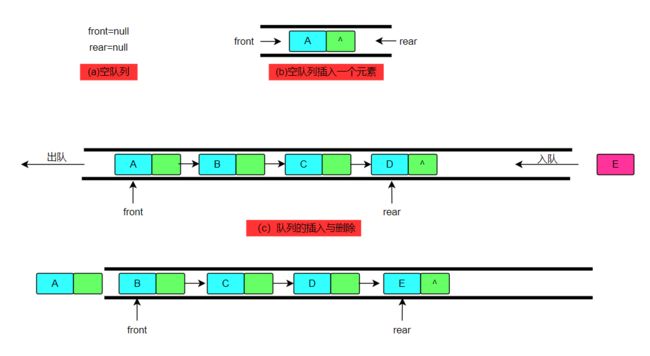
队列的链式存储类型描述如下:
typedef int QDataType;
typedef struct QNode //队列的每个节点(链表)
{
int data;
struct QNode* next;
}QNode;
typedef struct Queue //队列
{
QNode* front; //队头指针
QNode* rear; //队尾指针
int size; //队列元素个数
}Queue;
2.1 队列初始化
void QueueInit(Queue* q)
{
assert(q);
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
2.2 入队
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newNode = (QNode*)malloc(sizeof(QNode)); //创建结点
newNode->next = NULL;
newNode->data = data;
if (QueueEmpty(q)) //队列为空
{
q->front = newNode;
}
else //队列中已有元素
{
q->rear->next = newNode;
}
q->rear = newNode;
q->size++;
}
2.3 出队
void QueuePop(Queue* q)
{
assert(q);
assert(!QueueEmpty(q)); //断言:队列为空
QNode* delNode = q->front;
if (q->front == q->rear) //队列中只有一个元素
{
q->front = q->rear = NULL;
}
else //队列有多个元素
{
q->front = delNode->next;
}
free(delNode);
q->size--;
}
2.4 获取队头元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->front->data;
}
2.5 获取队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->rear->data;
}
2.6 获取队列中有效元素的个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
2.7 检测队列是否为空
int QueueEmpty(Queue* q)
{
assert(q);
return q->rear == NULL;
}
2.8 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
q->front = cur->next;
free(cur);
cur = q->front;
}
q->front = q->rear = NULL;
q->size = 0;
}
3. 源代码
3.1 queue.h
#include 3.2 queue.c
#include "Queue.h"
void QueueInit(Queue* q)
{
assert(q);
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newNode = (QNode*)malloc(sizeof(QNode));
newNode->next = NULL;
newNode->data = data;
if (QueueEmpty(q))
{
q->front = newNode;
}
else
{
q->rear->next = newNode;
}
q->rear = newNode;
q->size++;
}
void QueuePop(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
return;
}
QNode* delNode = q->front;
if (q->front == q->rear)
{
q->front = q->rear = NULL;
}
else
{
q->front = delNode->next;
}
free(delNode);
q->size--;
}
QDataType QueueFront(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->front->data;
}
QDataType QueueBack(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->rear->data;
}
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
int QueueEmpty(Queue* q)
{
assert(q);
return q->rear == NULL;
}
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
q->front = cur->next;
free(cur);
cur = q->front;
}
q->front = q->rear = NULL;
q->size = 0;
}
void QueuePrint(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
printf("%d--->", cur->data);
cur = cur->next;
}
printf("NULL\n");
}
void QueueTest()
{
Queue q;
QueueInit(&q);
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
QueuePush(&q, 5);
QueuePush(&q, 6);
QueuePrint(&q);
QueuePop(&q);
QueuePrint(&q);
int ret = QueueFront(&q);
printf("%d\n", ret);
ret = QueueBack(&q);
printf("%d\n", ret);
}
3.3 test.c
#include "Queue.h"
int main()
{
QueueTest();
return 0;
}
队列扩展:循环队列
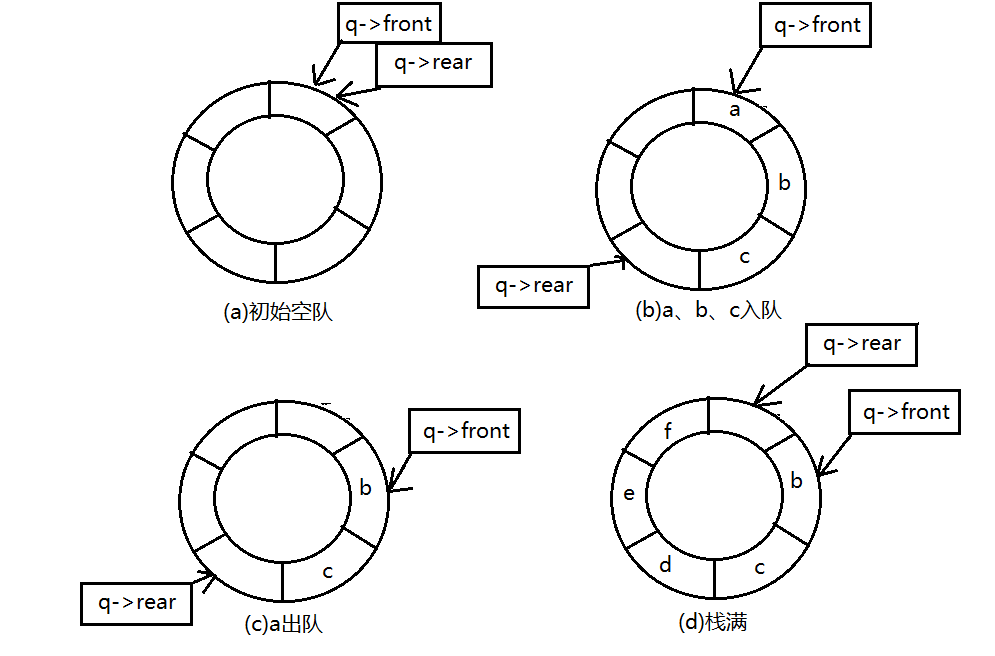
将循环队列臆造为一个环状的空间,即把存储队列元素的表从逻辑上视为一个环,称为循环队列。当队首指针q->front=maxszie-1后,再前进一个位置就自动到0。
初始化时:
q->front = q->rear = 0;
队首指针进1:q->front = (q->front + 1) % MaxSize;
队尾指针进1;q->rear = (q->rear + 1) % MaxSize;
队列长度:(q->rear + MaxSize - q->front) % MaxSize;
出队入队时:指针都按顺时针方向进1;
从下图可以看出对空的条件是q->front = q->rear ,若入队元素的速度快于出队元素的速度,则尾指针很快就会赶上队首指针,可以看出队满时也有q->front = q->rear。为了区分队满还是队空,我们选择浪费一个空间不存储元素,约定以队头指针在队尾指针的下一个位置作为队满的标志。
队满条件:
(q->rear + 1) % MaxSize == q->front;
队空条件:q->front = q->rear = 0;
队列中元素个数:(q->rear + MaxSize - q->front) % MaxSize。
总结
以上为对栈和队列的介绍,一定要注意最开始对其的初始化条件:比如栈的top指针到底指向哪里非常关键。相对来说栈与队列理解起来也比较轻松,主要是明白它们各自的属性特征。
文章若有不足的地方还请大佬指正!!!