吴恩达ML WEEK7 机器学习
吴恩达机器学习 第七周
- 0 总结
- 1 应用机器学习的建议
-
- 1.1 决定下一步做什么
- 1.2 评估一个假设
- 1.3 模型选择和交叉验证集
- 1.4 诊断偏差(bais)和方差(variance)
- 1.5 正则化和偏差/方差
- 1.6 学习曲线
- 1.7 决定接下来要做什么
- 2 机器学习系统的设计
-
- 2.1 首先要做什么
- 2.2 误差分析
- 2.3 类偏斜的误差度量
- 2.4 查准率和查全率之间的权衡
- 2.5 机器学习的数据
0 总结
学习时间:2022.10.17~2022.10.23
- 学习并区分交叉验证集、训练集、测试集。
- 学习评估模型。
- 学习过拟合、欠拟合及其解决方法。
- 绘制学习曲线。
- 学习类偏斜及改进方法,如使用查准率和查全率。
1 应用机器学习的建议
1.1 决定下一步做什么
在预测房价例子中,假如你已经完成了正则化线性回归,也就是最小化代价函数 J J J的值,如果你要将你的假设函数放到一组新的房屋样本上进行测试,发现在预测房价时产生了巨大的误差,现在你的问题是要想改进这个算法,接下来应该怎么办?
① 获得更多的训练样本——通常是有效的,但代价较大,下面的方法也可能有效,可考虑先采用下面的几种方法。
② 尝试减少特征的数量。
③ 尝试获得更多的特征。
④ 尝试增加多项式特征。
⑤ 尝试减少正则化程度 λ \lambda λ。
⑥ 尝试增加正则化程度 λ \lambda λ。
机器学习诊断法
通过执行这种测试,能够深入了解某种算法到底是否有用。
1.2 评估一个假设
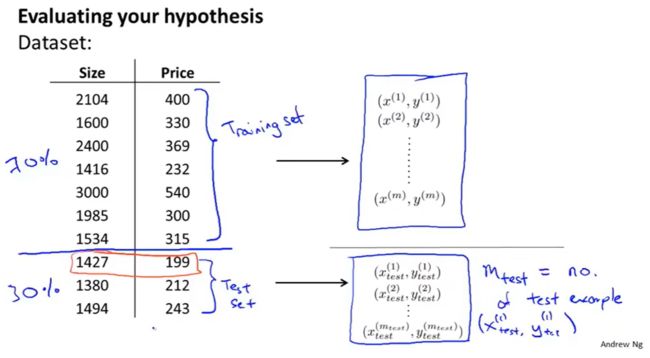
为了检验算法是否过拟合,我们将数据分成训练集和测试集,
通常用70%的数据作为训练集,用剩下30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据,如果数据有某种顺序,我们要对数据进行“洗牌”,然后再分成训练集和测试集。
m t e s t m_{test} mtest表示测试集的样本数量。
先利用训练集数据计算到 θ \theta θ,再代入 θ \theta θ,利用公式计算到测试集的误差。
有两种理解方式:
① 利用测试数据集来计算代价函数:
J t e s t ( θ ) = − 1 m t e s t ∑ i = 1 m t e s t log h θ ( x t e s t ( i ) ) + ( 1 − y t e s t ( i ) ) log h θ ( x t e s t ( i ) ) J_{test}{(\theta)} = -\frac{1}{{m}_{test}}\sum\limits_{i=1}^{m_{test}}\log{h_{\theta}(x^{(i)}_{test})}+(1-{y^{(i)}_{test}})\log{h_{\theta}(x^{(i)}_{test})} Jtest(θ)=−mtest1i=1∑mtestloghθ(xtest(i))+(1−ytest(i))loghθ(xtest(i))
② 错误分类的比率:
然后除以测试集的样本个数。
1.3 模型选择和交叉验证集
假设我们要在10个不同次数的二项式模型之间进行选择:
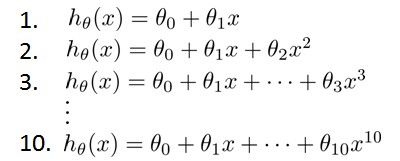
我们需要使用交叉验证集来帮助选择模型。
即:使用60%的数据作为训练集,使用 20%的数据作为交叉验证集,使用20%的数据作为测试集。
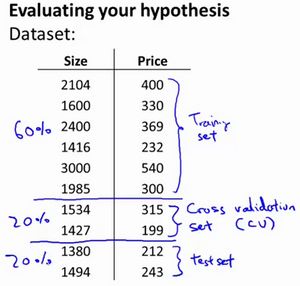
模型选择的方法为:
① 使用训练集训练出10个模型。
② 用10个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)。
③ 选取代价函数值最小的模型。
④ 用步骤3中选出的模型对测试集计算得出推广误差(代价函数的值)。
误差计算(线性回归)
Training error:
J t r a i n ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J_{train}(\theta) = \frac{1}{2m}\sum\limits_{i=1}\limits^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2 Jtrain(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
Cross Validation error:
J c v ( θ ) = 1 2 m c v ∑ i = 1 m ( h θ ( x ( i ) c v ) − y ( i ) c v ) 2 J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum\limits_{i=1}\limits^{m}(h_{\theta}(x^{(i)}{cv})-y^{(i)}{cv})^2 Jcv(θ)=2mcv1i=1∑m(hθ(x(i)cv)−y(i)cv)2
Test error:
J t e s t ( θ ) = 1 2 m t e s t ∑ i = 1 m t e s t ( h θ ( x ( i ) c v ) − y ( i ) c v ) 2 J_{test}(\theta)=\frac{1}{2m_{test}}\sum\limits_{i=1}\limits^{m_{test}}(h_{\theta}(x^{(i)}{cv})-y^{(i)}{cv})^2 Jtest(θ)=2mtest1i=1∑mtest(hθ(x(i)cv)−y(i)cv)2
1.4 诊断偏差(bais)和方差(variance)
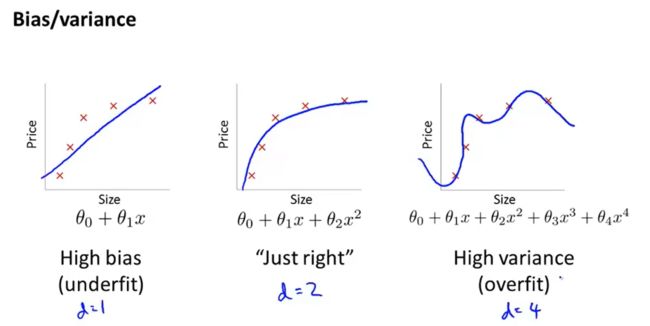
以 d d d表示多项式的次数。
可以得到:对于 d = 1 d=1 d=1的情况,会出现欠拟合(偏差大)。
对于 d = 4 d=4 d=4的情况,会出现过拟合(方差大)。
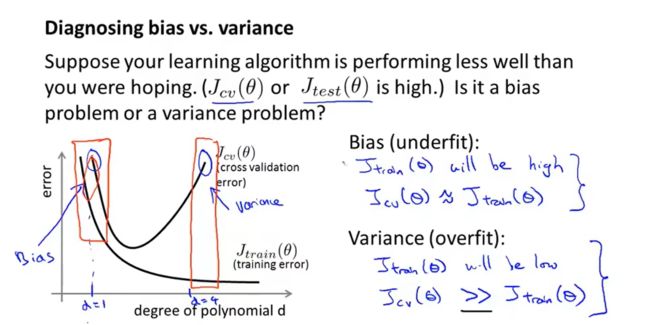
通过将训练集和交叉验证集的代价函数误差与多项式的次数( d d d)绘制在同一张图表上来帮助分析:
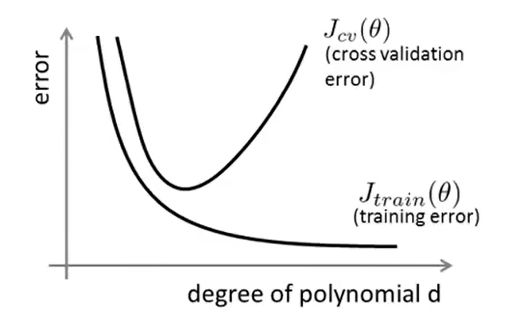
对于训练集,当 d d d 较小时,模型拟合程度更低,误差较大(欠拟合);随着 d d d 的增长,拟合程度提高,误差减小(过拟合)。
对于交叉验证集(或者测试集),当 d d d 较小时,模型拟合程度低,误差较大;但是随着 d d d 的增长,误差呈现先减小后增大的趋势(过拟合也会使验证集误差增大),转折点是我们的模型开始过拟合训练数据集的时候。
训练集误差高,训练集误差和交叉验证集误差近似时:偏差/欠拟合。
训练集误差低,交叉验证集误差远大于训练集误差时:方差/过拟合。
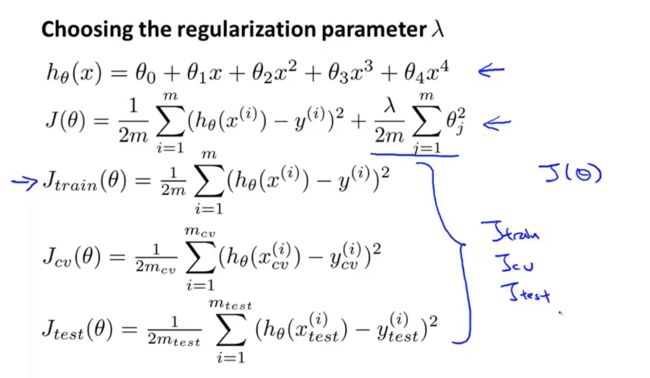
1.5 正则化和偏差/方差
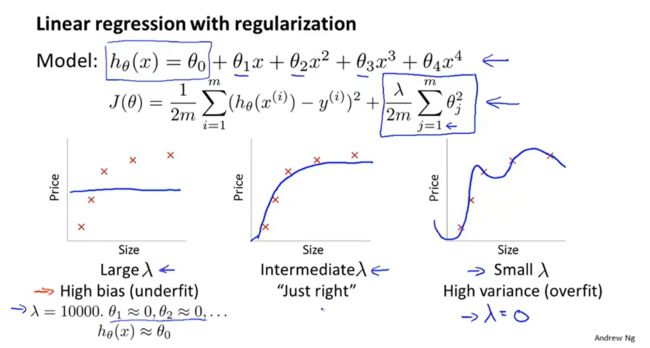
以 λ \lambda λ表示正则项的系数。
可以得到:对于 λ \lambda λ很大的情况,所有多项式系数都会趋近于0,会出现欠拟合(偏差大)。
对于 λ \lambda λ很小的情况,正则项约等于没有,会出现过拟合(方差大)。
注意,用来梯度下降的 J ( θ ) J(\theta) J(θ)使用的数据集就是训练集(train)。
选择合适的 λ \lambda λ
我们选择一系列的想要测试的 λ \lambda λ 值,通常是 0-10之间的呈现2倍关系的值(如: 0 , 0.01 , 0.02 , 0.04 , 0.08 , 0.15 , 0.32 , 0.64 , 1.28 , 2.56 , 5.12 , 10 0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共12个)。 我们同样把数据分为训练集、交叉验证集和测试集。

选择 λ \lambda λ的方法为:
① 使用训练集训练出12个不同程度正则化的模型(使训练集的 J ( θ ) J(\theta) J(θ)最小化,得到每个 λ \lambda λ对应的 Θ \Theta Θ)。
② 用12个模型分别对交叉验证集计算的出交叉验证误差 J c v ( θ ) J_{cv}(\theta) Jcv(θ)。
③ 选择得出交叉验证误差最小的模型,比如 Θ ( 5 ) \Theta^{(5)} Θ(5)。
④ 运用步骤3中选出模型对测试集计算得出推广误差 J t e s t ( θ ( 5 ) ) J_{test}(\theta^{(5)}) Jtest(θ(5)),我们也可以同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图表上:
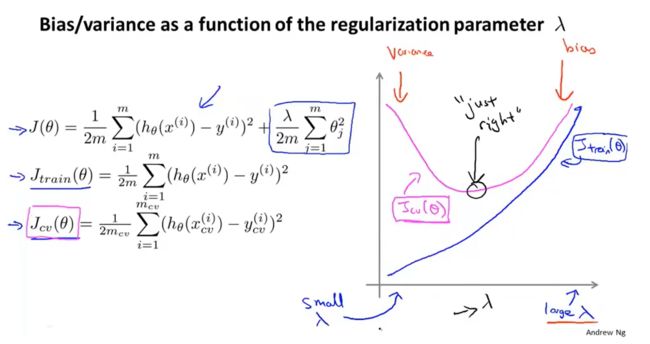
•当 λ \lambda λ 较小时,训练集误差较小(过拟合)而交叉验证集误差较大。
• 随着 λ \lambda λ 的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加。
1.6 学习曲线
定义
学习曲线:横坐标是训练集样本数量( m m m),纵坐标是误差(训练集误差和交叉验证集误差)。即,如果我们有100行数据,我们从1行数据开始,逐渐学习更多行的数据。以下都是理想情况下的学习曲线。
恰好拟合
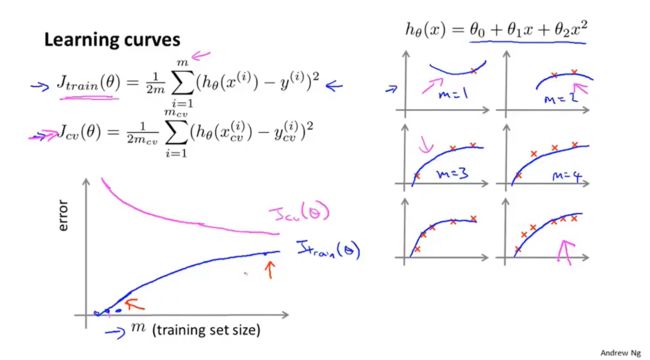
欠拟合
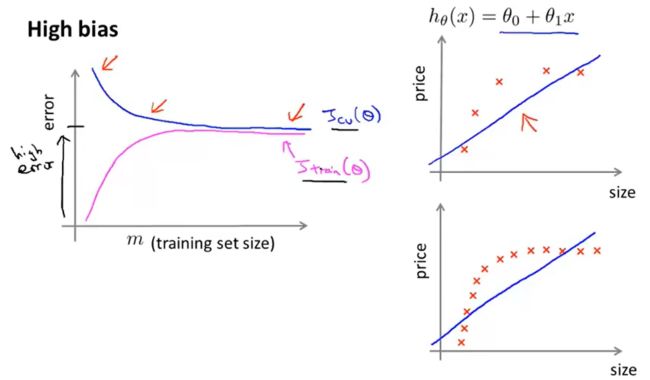
对于欠拟合情况,随着训练样本增大,最终 J c v ( θ ) J_{cv}(\theta) Jcv(θ)会约等于 J t r a i n ( θ ) J_{train}(\theta) Jtrain(θ),并且是一个很大的值。因此:
对于欠拟合,增大训练样本对改善算法无益。
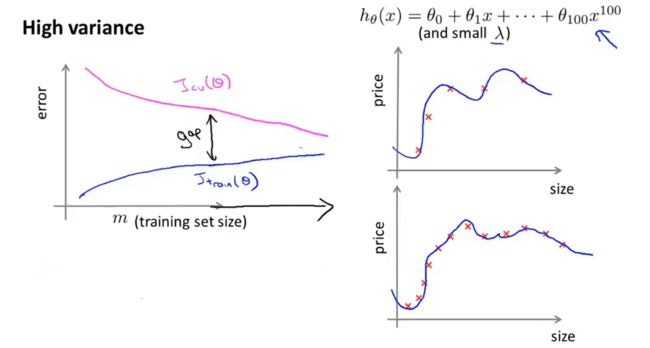
假设我们使用一个
非常高次的多项式模型,并且正则化非常小,可以看出,当交叉验证集误差远大于训练集误差时,往训练集增加更多数据可以提高模型的效果。
也就是说,在高方差/过拟合的情况下,增加更多数据到训练集可能可以提高算法效果。
1.7 决定接下来要做什么
回顾 1.1 中提出的六种可选的下一步,让我们来看一看我们在什么情况下应该怎样选择:
① 获得更多的训练样本——解决高方差(过拟合)
② 尝试减少特征的数量——解决高方差(过拟合)
③ 尝试获得更多的特征——解决高偏差(欠拟合)
④ 尝试增加多项式特征——解决高偏差(欠拟合)
⑤ 尝试减少正则化程度λ——解决高偏差(欠拟合)
⑥ 尝试增加正则化程度λ——解决高方差(过拟合)

(左图)使用
较小的神经网络,类似于参数较少的情况,容易导致高偏差和欠拟合,但计算代价较小。
(右图)使用较大的神经网络,类似于参数较多的情况,容易导致高方差和过拟合,虽然计算代价比较大,但是可以通过正则化手段来调整而更加适应数据。
总结:通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。
神经网络层数选择
通常从一层开始逐渐增加层数(一层、二层、三层…),为了更好地作选择,可以把数据分为训练集、交叉验证集和测试集,针对不同隐藏层层数的神经网络训练神经网络, 然后选择交叉验证集代价最小的神经网络。
2 机器学习系统的设计
2.1 首先要做什么
以一个垃圾邮件分类器算法为例
为了解决邮件是否是垃圾邮件这个问题,我们首先要做的决定是如何选择并表达特征向量 x x x。我们可以选择一个由100个最常出现在垃圾邮件中的词所构成的列表,根据这些词是否有在邮件中出现,来获得我们的特征向量(出现为1,不出现为0),维度为100×1。
如何改进这个分类算法:
① 收集更多的数据,让我们有更多的垃圾邮件和非垃圾邮件的样本。
② 基于邮件的路由信息开发一系列复杂的特征。
③ 基于邮件的正文信息开发一系列复杂的特征,包括考虑截词的处理。
④ 为探测刻意的拼写错误(把watch 写成w4tch)开发复杂的算法。
…
2.2 误差分析
误差分析也就是设定一个实数(如误差),来评估你的算法表现及性能。
构建一个学习算法的推荐方法为:
1.从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法。
2.绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择。
3.进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的样本,看看这些样本是否有某种系统化的趋势。
2.3 类偏斜的误差度量
什么是偏斜类
类偏斜情况表现为我们的训练集中有非常多的同一种类的样本,只有很少或没有其他类的样本。(比如样本中有99.5%都是良性肿瘤,只有0.5%是恶性肿瘤)
例子
我们希望用算法来预测癌症是否是恶性的,在我们的训练集中,只有0.5%的实例是恶性肿瘤。假设我们编写一个非学习而来的算法,在所有情况下都预测肿瘤是良性的(0),那么误差只有0.5%。然而我们通过训练而得到的神经网络算法却有1%的误差。这时,误差的大小是不能视为评判算法效果的依据的。
我们将算法预测分为四种情况:

横表示实际类,纵表示预测类。
①正确肯定(True Positive,TP):预测为真,实际为真
②正确否定(True Negative,TN):预测为假,实际为假
③错误肯定(False Positive,FP):预测为真,实际为假
④错误否定(False Negative,FN):预测为假,实际为真
定义:
查准率(Precision)=True Positive / #Predict Positive=TP/(TP+FP)。例,在所有我们预测有恶性肿瘤的病人中,实际上有恶性肿瘤的病人的百分比,越高越好。
查全率(Recall)=True Positive / #Acted Positive=TP/(TP+FN)。例,在所有实际上有恶性肿瘤的病人中,成功预测有恶性肿瘤的病人的百分比,越高越好。
这样,对于我们刚才那个总是预测病人肿瘤为良性的算法,其查全率是0。
2.4 查准率和查全率之间的权衡
例子回顾
在之前的肿瘤预测中,由于是偏斜类问题(良性肿瘤比较多),我们定义查准率(预测为1的样本中实际为1)和查全率(实际为1的样本预测为1),假使,我们的算法输出的结果在0-1 之间(用sigmoid函数限制)。
我们使用阀值0.5 来预测真和假,即:
如果 h θ ( x ) ≥ 0.5 h_{\theta}(x)\geq0.5 hθ(x)≥0.5,那么预测为1,即恶性肿瘤。
如果 h θ ( x ) < 0.5 h_{\theta}(x)<0.5 hθ(x)<0.5,那么预测为0,即良性肿瘤。
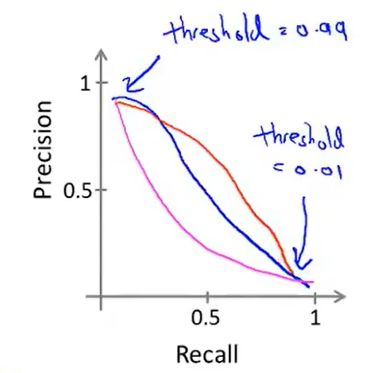
如果我们希望只在非常确信的情况下预测为真(肿瘤为恶性),即我们希望更高的查准率,我们可以使用比0.5更大的阀值,如0.7,0.9。这样做我们会减少错误预测病人为恶性肿瘤的情况,同时却会增加未能成功预测肿瘤为恶性的情况。(查准率高而查全率小)
如果 h θ ( x ) ≥ 0.9 h_{\theta}(x)\geq0.9 hθ(x)≥0.9,那么预测为1,即恶性肿瘤。
如果 h θ ( x ) < 0.9 h_{\theta}(x)<0.9 hθ(x)<0.9,那么预测为0,即良性肿瘤。
如果我们希望提高查全率,尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断,我们可以使用比0.5更小的阀值,如0.3。
如果 h θ ( x ) ≥ 0.3 h_{\theta}(x)\geq0.3 hθ(x)≥0.3,那么预测为1,即恶性肿瘤。
如果 h θ ( x ) < 0.3 h_{\theta}(x)<0.3 hθ(x)<0.3,那么预测为0,即良性肿瘤。
坐标上表示预测的阈值。
F1值
我们希望有一个帮助我们选择这个阀值的方法。一种方法是计算F1 值(F1 Score),其计算公式为:
F 1 S c o r e = 2 P R P + R {{F}_{1}}Score=2\frac{PR}{P+R} F1Score=2P+RPR(其中,P指查准率,R指查全率)。
如果P=0,R=0,此时F1=0。
如果P=1,R=1,此时F1=1。
(F1介于这两种情况之间)
我们选择使得F1值最高的阀值。
2.5 机器学习的数据
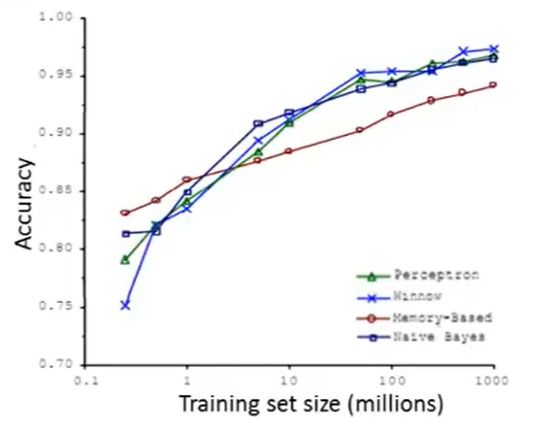
研究人员Michele Banko 和Eric Brill进行了一项有趣的研究,他们尝试通过机器学习算法来区分常见的易混淆的单词,他们尝试了许多种不同的算法(感知器、winnow…),并发现
数据量非常大时,这些不同类型的算法效果都很好。
大部分算法都有相似的性能,且随着训练集的数量增加,这些算法的性能也响应提升。事实上,如果你选择任意一个算法,可能是选择了一个"劣等的"算法,如果你给这个劣等算法更多的数据,那么从这些例子中看起来的话,它看上去很有可能会其他算法更好,甚至会比"优等算法"更好。
如果我们使用的算法有很多参数(比如逻辑回归和线性回归中的特征,神经网络中的隐藏单元…),那么训练集的误差会很小(过拟合)。
但是,如果我们使用的训练集非常大(远远大于参数个数),那么就不会出现过拟合现象,且训练集误差约等于测试集误差。
所以,当算法参数越多,数据越多,那么训练集和测试集的误差越小。
关键:
首先,选择合适的特征值。一个人类专家看到了特征值 x,能很有信心的预测出y值吗?因为这可以证明 y 可以根据特征值x被准确地预测出来。
其次,我们实际上能得到一组庞大的训练集,并且在这个训练集中训练一个有很多参数的学习算法吗?