YOLO 目标框回归（三）

边框预测公式分析 

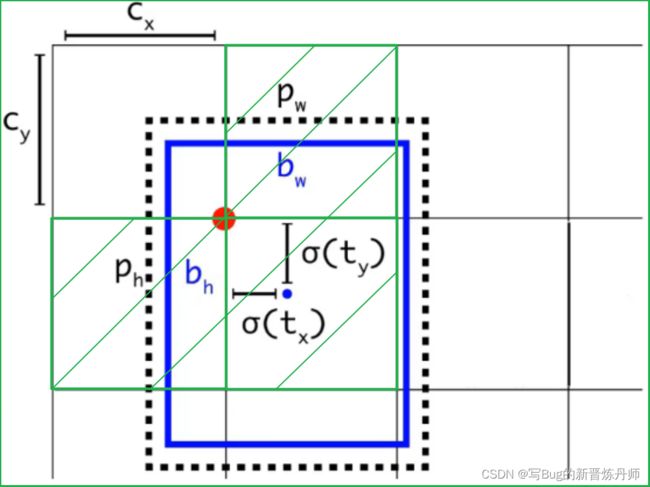
Cx，Cy 是 feature map 中 grid cell 的左上角坐标；Pw，Ph 是预设的 anchor box 映射到 feature map 中的宽和高。

最终得到的边框坐标值是 bx，by，bw，bh，即边界框 bbox 相对于 feature map 的位置和大小，是我们需要的预测输出坐标。但网络实际上的学习目标是 tx，ty，tw，th 偏移量（offsets），其中 tx，ty 是预测的坐标偏移值，tw，th 是尺度缩放，有了这４个offsets，可以根据公式去求得 bx，by，bw，bh。

问题1：为何不直接学习bx，by，bw，bh 呢？

解答：YOLO 的输出是卷积特征图，包含沿特征图深度的边界框属性（边界框属性由彼此堆叠的单元格预测得出）。如果需要在 (5,6) 处访问该单元格的第二个边框bbox，需要通过 map[5,6,(5+C):2*(5+C)] 将其编入索引。这种格式对于输出处理过程（例如通过目标置信度进行阈值处理、添加对中心的网格偏移、应用锚点等）很不方便，因此求偏移量即可。另外，通过学习偏移量，就可以通过网络原始给定的 anchor box 坐标经过线性回归（平移加尺度缩放）去逐渐靠近 groundtruth。

问题2：anchor box 的作用。

解答：YOLOv3 为每种 FPN 预测特征图（13x13，26x26，52x52）设定 3 种 anchor box，总共聚类出 9 种尺寸的 anchor box。在 COCO 数据集这 9 个 anchor box 是：(10x13)，(16x30)，(33x23)，(30x61)，(62x45)，(59x119)，(116x90)，(156x198)，(373x326)。

分配上，最小的 13x13 特征图上由于其感受野最大故应用最大的 anchor box (116x90、156x198、373x326)，适合检测较大的目标。中等的 26x26 特征图上由于其具有中等感受野，故应用中等的 anchor box (30x61、62x45、59x119)，适合检测中等大小的目标。较大的 52x52 特征图上由于其具有较小的感受野，故应用最小的 anchor box(10x13、16x30、33x23)，适合检测较小的目标。特征图的每个像素（即每个grid）都会有对应的三个 anchor box，如 13x13 特征图的每个 grid 都有三个 anchor box (116x90、156x198、373x326，这几个坐标需除以32缩放尺寸），即会使用 13×13×3=507 个 anchor box。

偏移量的求解

4 个坐标（tx，ty，tw，th）对于训练样本，在大多数文章里需要用到 ground truth 的真实框来求这4个坐标：

上述公式是 faster-rcnn 系列文章用到的公式，Pw，Ph 是预设的 anchor box 的在 feature map 上的宽和高。Gx，Gy，Gw，Gh 是 ground truth 在这个 feature map 的4个坐标。Gx、Gy、Gw、Gh 要先根据原图纵横比不变映射为416*416坐标下的一个子区域如416*312，取 min(w/img_w, h/img_h)这个比例来缩放成416*312，再填充为416*416，并把 x1，x2，y1，y2 的坐标系的换算从针对实际框的坐标系 416*312 变为 416*416 下，保证 bbox 不会扭曲，然后除以 stride 得到相对于 feature map 的坐标。

问题3：用 x，y 坐标减去 anchor box 的 x，y 坐标得到偏移量好理解，为何要除以 feature map 上 anchor box 的宽和高呢？

解答：可能是为了把绝对尺度变为相对尺度。不同尺度的 anchor box 如果都用 Gx-Px 来衡量显然不对，有的 anchor box 大，有的却很小。都用 Gx-Px 会导致不同尺度的 anchor box 权重相同，而大的 anchor box 能容忍大点的偏移量，小的 anchor box 对小偏移都很敏感，故除以宽和高可以权衡不同尺度下的预测坐标偏移量。

但是 yolov3 与 faster-rcnn 文章用到的公式在前两行不同，yolov3 里 Px，Py 换为了 feature map 上的 grid cell 左上角坐标 Cx，Cy了，即 yolov3 中是 Gx，Gy 减去 grid cell 左上角坐标 Cx，Cy。x，y 坐标并没有针对 anchon box 求偏移量，所以并不需要除以 Pw,Ph。这样可以直接求 bbox 中心距离 grid cell 左上角的坐标的偏移量。tw 和 th的公式 yolov3 和 faster-rcnn 系列是一样的，是物体所在边框的长宽和 anchor box 长宽之间的比率，不管 Faster-RCNN 还是 YOLO，都不是直接回归 bounding box 的长宽而是尺度缩放到对数空间。

问题4：为何不是直接回归 bounding box 的长宽，而是尺度缩放到对数空间？

解答：怕训练带来不稳定的梯度。如果不做变换，直接预测相对形变 tw 和 th，那么要tw，th>0。因为框的宽高不可能是负数。这样，是在做一个有不等式条件约束的优化问题，没法直接用 SGD 来做。所以先取一个对数变换，将其不等式约束去掉。

anchors 与 gt 的匹配

这里就有个重要的疑问了，一个尺度的feature map有三个anchors，那么对于某个ground truth框，究竟是哪个anchor负责匹配它呢？和YOLOv1一样，对于训练图片中的ground truth，若其中心点落在某个cell内，那么该cell内的3个anchor box负责预测它，具体是哪个anchor box预测它，需要在训练中确定，即由那个与ground truth的IOU最大的anchor box预测它，而剩余的2个anchor box不与该ground truth匹配。

YOLOv3 需要假定每个 cell 至多含有一个 grounth truth，而在实际上基本不会出现多于 1 个的情况。与 ground truth 匹配的 anchor box 计算坐标误差、置信度误差（此时target为1）以及分类误差，而其它的 anchor box 只计算置信度误差（此时target为0）。在训练过程中划分正负样本是非常重要的，因为 anchor 很多，只有对一大堆 anchor box 划分了正负样本，才能有效地用正样本参与损失函数训练。但问题是三个检测层，那么多 anchor box，如果只把 gt 匹配一个 anchor，那么正样本数量会极其稀少，对训练极为不利。

问题5：如何划分正负样本

解答：假设 IOU 阈值为0.7，所有锚点框与真实标签进行匹配，需要构造 IOU 矩阵，每一行代表一个锚点框，行数代表 anchor box 数量，每一列代表一个真值框，列数代表gt的个数。然后执行 3 个标准：

• 对于任何一个锚点框，与所有标签的最大 IOU 小于 0.3，则视为负样本
• 对于任何一个真值，与其有最大 IOU 的瞄点框视为正样本
• 对于任何一个瞄点框，与所有真值框的最大 IOU 大于 0.7 则视为正样本。

这样的三个标准顺序不能变动，保证了多个瞄点框对应一个真值，而一个真值框不能对应多个瞄点框。

根据偏移量求得真正的检测框

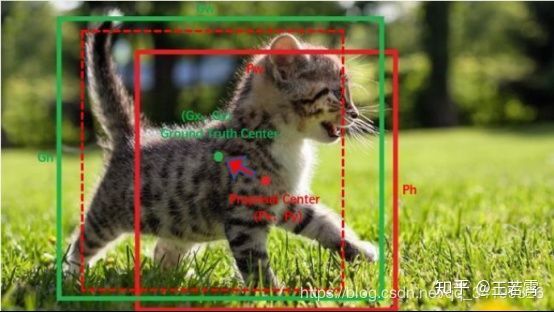
有了平移（tx,ty）和尺度缩放（tw,th），就能让 anchor box 经过微调与 grand truth 重合。如下图，红色框为 anchor box，绿色框为 Ground Truth，平移+尺度缩放可实线红色框先平移到虚线红色框，然后再缩放到绿色框。边框回归最简单的想法就是通过平移加尺度缩放进行微调嘛。

问题6：边框回归为何只能微调？

当输入的 Proposal 与 Ground Truth 相差较小时，即IOU很大时，可以认为这种变换是线性变换， 可以用线性回归（线性回归即给定输入的特征向量 X，学习一组参数 W，经过线性回归后的值跟真实值 Y(Ground Truth)非常接近）来建模对窗口进行微调，否则会导致训练的回归模型不 work（当 Proposal 与 GT 离得较远，就是复杂的非线性问题，此时用线性回归建模不合理） 

那么训练时用的 ground truth 的4个坐标去做差值和比值得到 tx，ty，tw，th，测试时就用预测的bbox 就好了，公式修改就简单了，把 Gx 和 Gy 改为预测的x，y；Gw、Gh改为预测的w，h即可。

网络可以不断学习 tx,ty,tw,th 偏移量和尺度缩放，预测时使用这4个offsets求得bx,by,bw,bh即可。

问题7：tx,ty为何要sigmoid一下啊？

解答：前面讲了在 yolov3 中没有让 Gx - Cx 后除以 Pw 得到 tx，而是直接 Gx - Cx 得到 tx，这样会有问题是导致 tx 比较大且很可能 >1（因为没有除以 Pw 归一化尺度）。用 sigmoid 将 tx，ty 压缩到 [0,1] 区间內，可以有效的确保目标中心处于执行预测的网格单元中，防止偏移过多。举个例子，网络不会预测边界框中心的确切坐标而是预测与预测目标的 grid cell 左上角相关的偏移 tx，ty。如 13*13 的 feature map 中，某个目标的中心点预测为（0.4，0.7），它的 Cx，Cy 即中心落入的 grid cell 坐标是（6，6），则该物体在 feature map 中的中心实际坐标显然是（6.4，6.7），这种情况没毛病。但若 tx，ty 大于1，比如（1.2，0.7）则该物体在 feature map 的的中心实际坐标是（7.2，6.7），这时候该物体中心在这个物体所属 grid cell 外面了，但（6，6）这个 grid cell 却检测出我们这个单元格内含有目标的中心（yolo 是采取物体中心归哪个 grid cell 整个物体就归哪个 grid celll了），这样就矛盾了，因为左上角为（6，6）的 grid cell 负责预测这个物体，这个物体中心必须出现在这个grid cell中而不能出现在它旁边网格中，一旦 tx，ty 算出来大于 1 就会引起矛盾，因而必须归一化。
扩展：当然 yolov5 里就不再是这样了，其为了使得有更多目标归属于每个格子，就不再限定偏移量为 [0-1]，而是能够使得隔壁的目标也属于当前格子。

问题8：最后两行公式，tw 为何要指数呀？

解答：因为 tw，th 是 log 尺度缩放到对数空间了，当然要指数回来，而且这样可以保证大于0。至于左边乘以 Pw，Ph 是因为 tw=log(Gw/Pw) 当然应该乘回来得到真正的宽高。　　

记 feature map 大小为 Ｗ*Ｈ（如13*13），可将 bbox 相对于整张图片的位置和大小计算出来（使4个值均处于[0,1]区间内）约束了bbox的位置预测值到[0,1]会使得模型更容易稳定训练（如果不是[0,1]区间，yolo的每个bbox的维度都是85，前5个属性是(Cx,Cy,w,h,confidence)，后80个是类别概率，如果坐标不归一化，和这些概率值一起训练肯定不收敛）。

只需要把之前计算的bx,bw都除以W,把by,bh都除以H。即

YOLOv5采用跨邻域网格的匹配策略，从而得到更多的正样本anchor，可加速收敛。

从当前网络的上、下、左、右的四个网格中找到离目标中心点最近的两个网格，再加上当前网格共三个网格进行匹配。

参考文章：超详细的Yolo检测框预测分析 - 知乎 (zhihu.com)