DEFORMABLE DETR学习笔记
DEFORMABLE DETR学习笔记
DEFORMABLE DETR: DEFORMABLE TRANSFORMERS FOR END-TO-END OBJECT DETECTION
ABSTRACT
DETR最近被提出,以消除在目标检测中需要许多手工设计的组件,同时展示良好的性能。但由于Transformer注意模块在处理图像特征映射时的局限性,其收敛速度慢,特征空间分辨率有限。为了缓解这些问题,我们提出了Deformable 的DETR,它的注意模块只关注参考点周围的一小部分关键采样点。Deformable 的DETR可以比DETR(特别是在小物体上)获得更好的性能,且训练时间少10倍。在COCO基准上的大量实验证明了我们方法的有效性。代码发布在
https:// github.com/fundamentalvision/Deformable-DETR。
1、INTRODUCTION
现代目标检测器采用了许多手工制作的组件(Liu等人,2020),例如锚点生成、基于规则的训练目标分配、非最大抑制(NMS)后处理。它们不是完全端到端。最近,Carion等人(2020)提出了DETR以消除对此类手工制作组件的需求,并构建了第一个完全端到端对象检测器,实现了非常有竞争力的性能。DETR通过结合卷积神经网络(CNNs)和变压器(Vaswani等人,2017)编码器-解码器,利用了一个简单的架构。他们利用Transformers的多功能和强大的关系建模能力,在适当设计的训练信号下,取代手工制作的规则。
尽管DETR的设计很有趣,性能也很好,但它也有自己的问题:(1)与现有的目标检测器相比,它需要更长的训练时间才能收敛。例如,在COCO (Lin et al., 2014)基准上,DETR需要500个epoch才能收敛,这比Faster R-CNN (Ren et al., 2015)慢约10到20倍。(2) DETR在检测小物体时性能相对较低。现代物体探测器通常利用多尺度特征,从高分辨率特征图中检测小物体。同时,高分辨率的特征图给DETR带来了不可接受的复杂性。上述问题主要是由于Transformer组件在处理图像特征图时存在不足。在初始化时,注意模块对特征图中的所有像素施加几乎一致的注意权重。长时间的训练是必要的,以学习注意力权重集中在稀疏的有意义的位置。另一方面,变压器编码器的注意权值计算是二次元计算。因此,处理高分辨率特征图具有很高的计算复杂度和存储复杂度。
在图像领域,Deformable 卷积(Dai et al., 2017)是处理稀疏空间位置的一种强大而有效的机制。它自然避免了上述问题。而它缺乏元素关系建模机制,而元素关系建模是DETR成功的关键。
在本文中,我们提出了一种Deformable 的DETR算法,它能有效地解决DETR算法收敛速度慢、复杂度高的问题。它结合了Deformable 卷积的稀疏空间采样和变压器的关系建模能力。我们提出了一种Deformable 注意模块,它关注一小组采样位置,作为从所有特征图像素中筛选出突出关键元素的预过滤器。该模块可以很自然地扩展到聚合多尺度特征,而无需FPN的帮助(Lin等人,2017a)。在变形DETR中,我们使用(多尺度)变形注意模块来代替变形注意模块处理特征图,如图1所示。
由于其快速收敛、计算和存储效率,可变形的DETR为我们开发端到端对象检测器的变体提供了可能性。我们探索了一种简单有效的迭代边界盒优化机制来提高检测性能。我们还尝试了两阶段的变形DETR,其中区域建议也由变形DETR的变体生成,并进一步输入到解码器中进行迭代边界框细化。
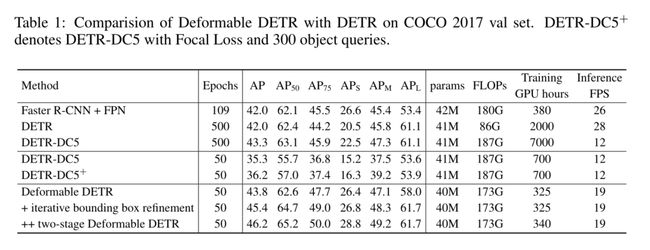
在COCO (Lin et al., 2014)基准上的大量实验证明了我们方法的有效性。与DETR相比,变形DETR可以获得更好的性能(特别是在小物体上),训练时间减少10倍。提出的两级可变形DETR可以进一步提高性能。代码发布在https://github。com/fundamentalvision/Deformable-DETR。
2 、RELATED WORK
Efficient Attention Mechanism
Transformers(V aswani et al., 2017)涉及自我注意和交叉注意机制。transformer最著名的问题之一是大量关键元素的高时间和内存复杂性,这在许多情况下阻碍了模型的可伸缩性。近年来,人们为解决这一问题做出了许多努力(Tay et al., 2020b),在实践中大致可分为三类。
第一类是在键上使用预先定义的稀疏注意模式。最直接的范式是将注意力模式限制为固定的局部窗口。大部分作品(Liu et al., 2018a;Parmar等人,2018;儿童等,2019;黄等,2019;Ho等,2019;王等,2020a;胡等,2019;Ramachandran等人,2019;邱等,2019;Beltagy等人,2020年;安斯利等人,2020年;Zaheer等人,2020)遵循这一范式。虽然将注意力模式限制在局部社区可以降低复杂性,但它会丢失全局信息。为了补偿,Child等人(2019);黄等人(2019);Ho等人(2019);Wang等人(2020a)参加了关键要素以固定的间隔来显著增加键上的接受场。Beltagy等人(2020年);Ainslie等人(2020);Zaheer等人(2020)允许少量特殊令牌访问所有关键元素。Zaheer等人(2020年);Qiu等人(2019)还添加了一些预先固定的稀疏注意模式,直接关注远处的关键元素。
第二类是学习依赖数据的稀疏注意。Kitaev等人(2020)提出了一种基于局部敏感哈希(LSH)的注意,它将查询和关键元素哈希到不同的容器。Roy等人(2020)提出了一个类似的想法,k-means找出了最相关的键。Tay等人(2020a)学习块排列以获得块级稀疏注意。
第三类是探索自我注意中的低阶属性。Wang等人(2020b)通过尺寸维度上的线性投影而不是通道维度来减少关键元素的数量。Katharopoulos等人(2020年);Choromanski等人(2020)通过核化近似重写了自我注意力的计算。
在图像领域,有效注意机制的设计(例如,Parmar等人(2018);Child等人(2019);黄等人(2019);Ho等人(2019);Wang等(2020a);Hu等人(2019);Ramachandran等人(2019))仍然局限于第一类。尽管理论上复杂性降低了,Ramachandran等人(2019);Hu等人(2019)承认,由于内存访问模式的内在限制,这种方法在实现上比具有相同FLOPs的传统卷积慢得多(至少慢3倍)。
另一方面,如Zhu et al. (2019a)所讨论的,卷积有多种变体,如可变形卷积(Dai et al., 2017;Zhu等人,2019b)和动态卷积(Wu等人,2019),这也可以被视为自我注意机制。特别是可变形卷积在图像识别上比Transformer的自注意更有效。同时,缺乏元素关系建模机制。
我们提出的可变形注意模块是受到可变形卷积的启发,属于第二类。它只关注由查询元素的特征预测的一小部分固定的采样点集合。不同于Ramachandran等人(2019);Hu等人(2019)认为,在相同的FLOPs下,变形注意仅略慢于传统卷积。
Multi-scale Feature Representation for Object Detection
物体检测的主要困难之一是有效地表示不同尺度的物体。现代物体探测器通常利用多尺度特征来适应这一点。作为开创性的工作之一,FPN (Lin et al., 2017a)提出了一种自上而下的路径来结合多尺度特征。PANet (Liu et al., 2018b)进一步在FPN的顶部增加了一条自底向上的路径。Kong等人(2018)通过全球注意力操作综合了来自所有尺度的特征。Zhao等人(2019)提出了一个u形模块来融合多尺度特征。最近,NAS-FPN (Ghiasi等人,2019)和Auto-FPN (Xu等人,2019)被提出通过神经结构搜索自动设计跨尺度连接。Tan等人(2020)提出了BiFPN,这是PANet的重复简化版本。我们提出的多尺度变形注意模块可以通过注意机制自然聚合多尺度特征图,而不需要这些特征金字塔网络的帮助。
3 、REVISITING TRANSFORMERS AND DETR
Multi-Head Attention in Transformers
变压器(V aswani et al., 2017)是一种基于注意机制的网络架构,用于机器翻译。给定一个查询元素(如输出句中的目标词)和一组关键元素(如输入句中的源词),多头注意模块根据衡量查询键对相容性的注意权重自适应聚合关键内容。为了使模型能够聚焦于来自不同表示子空间和不同位置的内容,对不同注意头的输出采用可学习权值进行线性聚合。设 q ∈ Ω q q∈Ω_q q∈Ωq索引一个具有表示特征 z q ∈ R C z_q∈R^C zq∈RC的查询元素, k ∈ Ω k k∈Ω_k k∈Ωk索引一个具有表示特征 x k ∈ R C x_k∈R^C xk∈RC的关键元素,其中C为特征维, Ω q Ω_q Ωq和 Ω k Ω_k Ωk分别表示查询和关键元素的集合。然后计算多头注意特征
Transformers有两个已知问题。其一是Transformers在融合之前需要很长的训练计划。假设查询和关键元素的个数分别为 N q 和 N k N_q和N_k Nq和Nk。通常情况下,在适当的参数初始化下, U m z q U_mz_q Umzq和 V m x k V_mx_k Vmxk遵循均值为0、方差为1的分布,使得在 N k N_k Nk较大时,注意权重 A m q k ≈ 1 / N k A_{mqk}≈1/Nk Amqk≈1/Nk。这将导致输入特征的模糊梯度。因此,需要长时间的训练计划,以便注意力的权重可以集中在特定的关键。在图像域中,关键元素通常是图像像素, N k N_k Nk可能非常大,收敛过程非常繁琐。
另一方面,由于大量的查询和关键元素,多头注意的计算和存储复杂度可能非常高。公式1的计算复杂度为。在图像域中,查询和关键元素都是像素, O ( N q C 2 + N k C 2 + N q N k C ) O\left(N_{q} C^{2}+N_{k} C^{2}+N_{q} N_{k} C\right) O(NqC2+NkC2+NqNkC),复杂度以第三项为主,如 O ( N q N k C ) O(N_qN_kC) O(NqNkC)。因此,多头注意模块的复杂度随特征图的大小呈二次增长。
DETR
DETR (Carion等人,2020年)建立在Transformer编码器-解码器架构之上,结合了基于集的匈牙利损耗,通过二部匹配对每个地面真理边界框进行唯一的预测。下面我们简要回顾一下网络架构。
给定由CNN主干(例如,ResNet (He et al., 2016))提取的输入特征映射 x ∈ R C × H × W x∈R^{C×H×W} x∈RC×H×W, DETR利用标准的Transformer编码器-解码器体系结构将输入特征映射转换为一组对象查询的特征。在目标查询特征(由解码器产生)的基础上增加一个三层前馈神经网络(FFN)和一个线性投影作为检测头。FFN作为回归分支预测边界盒坐标b∈[0,1],其中 b = b x , b y , b w , b h b = {b_x, b_y, b_w, b_h} b=bx,by,bw,bh编码归一化的盒中心坐标、盒高和宽度(相对于图像大小)。线性投影作为分类分支产生分类结果。
对于DETR中的Transformer编码器,查询和关键元素都是特征映射中的像素。输入是ResNet特征映射(带有编码的位置嵌入)。设H和W分别表示特征映射的高度和宽度。自我注意的计算复杂度为 O ( H 2 W 2 C 2 ) O(H^2 W^2 C^2) O(H2W2C2),随空间大小呈二次增长。
对于DETR中的Transformer解码器,输入既包括来自编码器的特征映射,也包括由可学习位置嵌入表示的N个对象查询(例如N = 100)。解码器中有两种注意模块,即交叉注意模块和自我注意模块。在交叉注意模块中,对象查询从特征映射中提取特征。查询元素是对象查询,关键元素是编码器的输出特征映射。其中, N q = N , N k = H × W N_q = N, N_k = H × W Nq=N,Nk=H×W,交叉注意的复杂度为 O ( H W C 2 + N H W C ) O(HW C^2 + N HW C) O(HWC2+NHWC),复杂度随特征图空间大小呈线性增长。在自我注意模块中,对象查询彼此交互,以便捕获它们之间的关系。查询和关键元素都是对象查询。其中, N q = N k = N N_q = N_k = N Nq=Nk=N,自注意模块的复杂度为 O ( 2 N C 2 + N 2 C ) O(2N C^2 + N^2 C) O(2NC2+N2C)。在对象查询数量适中的情况下,复杂性是可以接受的。
DETR是一种吸引人的目标检测设计,它消除了许多手工设计的组件的需要。然而,它也有自己的问题。这些问题主要是由于Transformer在处理图像特征映射方面的注意不足,这是其中的关键因素:(1)DETR在检测小物体方面的性能相对较低。现代物体探测器使用高分辨率特征图来更好地检测小物体。然而,高分辨率的特征映射会导致DETR的变压器编码器中的自我注意模块的复杂度不可接受,其复杂度与输入特征映射的空间大小呈二次曲线关系。(2)与现代目标检测器相比,DETR需要更多的训练周期才能收敛。这主要是因为处理图像特征的注意模块难以训练。例如,在初始化时,交叉注意模块在整个特征图上几乎是平均注意。然而,在训练结束时,注意地图被学习到非常稀疏,只专注于对象四肢。似乎DETR需要一个很长的训练计划来学习注意力地图中如此显著的变化。
4 、METHOD
4.1 DEFORMABLE TRANSFORMERS FOR END-TO-END OBJECT DETECTION
Deformable Attention Module
将Transformer注意应用于图像特征映射的核心问题是它将查看所有可能的空间位置。为了解决这个问题,我们提出了一个可变形的注意模块。受可变形卷积的启发(Dai等人,2017;Zhu等人,2019b),变形注意模块只关注参考点周围的一小部分关键采样点,而不考虑特征图的空间大小,如图2所示。通过为每个查询只分配少量固定数量的键,可以缓解收敛和特征空间分辨率的问题。
给定一个输入特征映射 x ∈ R C × H × W x∈R^{C×H×W} x∈RC×H×W,设q索引一个具有内容特征 z q z_q zq和二维参考点 p q p_q pq的查询元素,可变形注意特征计算为
其中m表示注意头,k表示采样键,k表示总采样键数( k ≪ H W k \ll HW k≪HW)。 ∆ p m q k ∆p_{mqk} ∆pmqk和 A m q k A_{mqk} Amqk分别为第m个注意头中第k个采样点的采样偏移量和注意权重。标量注意权重 A m q k A_{mqk} Amqk在[0,1]范围内,归一化为 ∑ k = 1 K A m q k = 1. Δ p m q k ∈ R 2 \sum_{k=1}^{K} A_{m q k}=1 . \Delta \boldsymbol{p}_{m q k} \in \mathbb{R}^{2} ∑k=1KAmqk=1.Δpmqk∈R2为二维实数,值域无约束。由于 p q + ∆ p m q k p_q+∆p_{mqk} pq+∆pmqk为分数阶,计算 x ( p q + ∆ p m q k ) x(p_q+∆p_{mqk}) x(pq+∆pmqk)采用双线性插值方法,如Dai等(2017)。 ∆ p m q k ∆p_{mqk} ∆pmqk和 A m q k A_{mqk} Amqk都是通过查询特征 z q z_q zq上的线性投影得到的。在实现中,查询特征 z q z_q zq被馈送给一个3M K通道的线性投影算子,其中前2M K通道编码采样偏移量 ∆ p m q k ∆p_{mqk} ∆pmqk,其余M K通道被馈送给一个softmax算子获得注意权值 A m q k A_{mqk} Amqk。
设计了可变形注意模块,将卷积特征映射作为关键元素进行处理。设 N q N_q Nq为查询元素个数,当M K较小时,变形注意模块的复杂度为 O ( 2 N q C 2 + min ( H W C 2 , N q K C 2 ) ) O\left(2 N_{q} C^{2}+\min \left(H W C^{2}, N_{q} K C^{2}\right)\right) O(2NqC2+min(HWC2,NqKC2))(详见附录A.1)。当应用于DETR编码器时, N q = H W N_q = HW Nq=HW,复杂度为 O ( H W C 2 ) O(HW C^2) O(HWC2),复杂度与空间尺寸呈线性关系。当它作为交叉注意模块应用时在DETR解码器中, N q = N N_q = N Nq=N (N为对象查询次数),复杂度为 O ( N K C 2 ) O(N KC^2) O(NKC2),与空间大小HW无关。
Multi-scale Deformable Attention Module
大多数现代目标检测框架受益于多尺度特征映射(Liu等人,2020)。我们提出的可变形注意模块可以自然地扩展到多尺度特征图。
设 { x l } l = 1 L \left \{ x^l \right \}^{L}_{l=1} {xl}l=1L为输入的多尺度特征映射,其中 x l ∈ R C × H l × W l x^l∈R^{C×H_l×W_l} xl∈RC×Hl×Wl。设 p q ^ ∈ [ 0 , 1 ] 2 \hat{p_q} ∈[0,1]^2 pq^∈[0,1]2为每个查询元素q的参考点归一化坐标,则应用多尺度变形注意模块为
其中m表示注意头,l表示输入特征水平,k表示采样点。 ∆ p m l q k ∆p_{mlqk} ∆pmlqk和 A m l q k A_{mlqk} Amlqk分别为第l个特征层第k个采样点的采样偏移量和第m个注意头的注意权重。标量注意权重 A m l q k A_{mlqk} Amlqk归一化为 ∑ l = 1 L ∑ k = 1 K A m l q k = 1 \sum_{l=1}^{L} \sum_{k=1}^{K} A_{m l q k}=1 ∑l=1L∑k=1KAmlqk=1。这里,为了尺度公式的清晰性,我们使用归一化坐标 p q ^ ∈ [ 0 , 1 ] 2 \hat{p_q} ∈[0,1]^2 pq^∈[0,1]2,其中归一化坐标(0,0)和(1,1)分别表示图像左上角和右下角的角。公式3中的函数 φ l ( p q ^ ) φ_l(\hat{p_q}) φl(pq^)将归一化坐标 p q ^ \hat{p_q} pq^重新缩放到l-th层的输入特征映射。多比例尺可变形注意与之前的单比例尺版本非常相似,只是它从多比例尺特征图中采样LK点,而不是从单比例尺特征图中采样K点。
当 L = 1 , K = 1 , w m ′ ∈ R C v × C L = 1, K = 1, w^{'}_m∈R^{C_v×C} L=1,K=1,wm′∈RCv×C固定为单位矩阵时,所提出的注意模块将退化为可变形卷积(Dai et al., 2017)。可变形卷积是为单尺度输入设计的,每个注意头只关注一个采样点。然而,我们的多尺度变形注意从多尺度输入中查看多个采样点。提出的(多尺度)变形注意模块也可以被视为变压器注意的有效变体,其中通过变形采样位置引入预滤波机制。当采样点遍历所有可能的位置时,所提出的注意模块等价于变压器注意。
Deformable Transformer Encoder
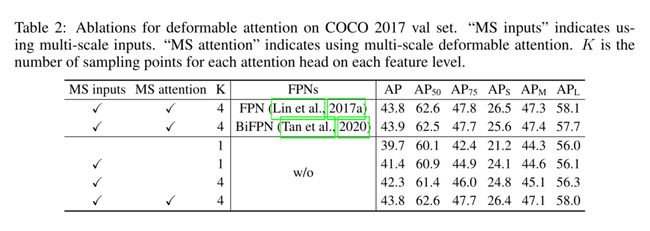
我们用所提出的多尺度变形注意模块替换了der中处理特征映射的Transformer注意模块。编码器的输入和输出都是具有相同分辨率的多比例尺特征映射。在编码器中,我们从ResNet (He et al., 2016)中C3到C5阶段的输出特征映射(通过1 × 1卷积转换)中提取多尺度特征映射 { x l } l = 1 L − 1 ( L = 4 ) \left \{ x^l \right \}^{L-1}_{l=1}(L=4) {xl}l=1L−1(L=4),其中 C l C_l Cl的分辨率比输入图像低 2 l 2^l 2l。最低分辨率的特征图 x L x^L xL是在最后的C5阶段通过3 × 3 stride 2卷积得到的,记为C6。所有多尺度特征图均为C = 256通道。注意,我们没有使用FPN (Lin等人,2017a)中的自上而下结构,因为我们提出的多尺度变形注意本身可以在多尺度特征图之间交换信息。多尺度特征图的构造也在附录A.2中说明。5.2节的实验表明,添加FPN并不会提高性能。
在编码器多比例尺可变形注意模块的应用中,输出是与输入分辨率相同的多比例尺特征映射。键和查询元素都是来自多尺度特征映射的像素。对于每个查询像素,参考点就是它本身。为了识别每个查询像素所在的特征级别,除了位置嵌入之外,我们还在特征表示中添加了一个标度级嵌入,称为 e l e_l el。与固定编码的位置嵌入不同,尺度级嵌入 { e l } l = 1 L \left \{ e^l \right \}^{L}_{l=1} {el}l=1L是随机初始化的,并与网络联合训练。
**Deformable Transformer Decoder **
译码器中有交叉注意模块和自我注意模块。这两种注意模块的查询元素都是对象查询。在交叉注意模块中,对象查询从特征映射中提取特征,其中关键元素来自编码器的输出特征映射。在自我注意模块中,对象查询彼此交互,其中关键元素是对象查询。由于我们提出的可变形注意模块是为处理卷积特征映射作为关键元素而设计的,因此我们只将每个交叉注意模块替换为多尺度可变形注意模块,而不改变自注意模块二维归一化坐标通过一个可学习的线性投影和一个sigmoid函数,在对象查询嵌入中预测参考点。
由于多尺度变形注意模块提取参考点周围的图像特征,我们让检测头预测边界盒作为参考点的相对偏移量,进一步降低了优化难度。以参考点作为盒心的初始猜想。探测头预测参考点的相对偏移量。详见附录A.3。这样,学习到的解码器注意将与预测的边界框有很强的相关性,这也加速了训练收敛。
通过将DETR中的Transformer注意模块替换为可变形注意模块,我们建立了一个高效、快速收敛的检测系统,称为可变形DETR(如图1所示)。
4.2 ADDITIONAL IMPROVEMENTS AND VARIANTS FOR DEFORMABLE DETR
由于其快速收敛、计算和存储效率,可变形的DETR为我们开发端到端对象检测器的各种变体提供了可能性。由于篇幅所限,这里只介绍这些改进和变体的核心思想。实施详情载于附录A.4。
Iterative Bounding Box Refinement
这是受光流估计中迭代细化的启发(Teed & Deng, 2020)。我们建立了一种简单有效的迭代边界盒优化机制来提高检测性能。在这里,每个解码器层基于前一层的预测细化边界框。
Two-Stage Deformable DETR
在原始的DETR中,解码器中的对象查询与当前图像无关。受两阶段对象检测器的启发,我们探索了一种变形DETR的变体,用于生成区域建议作为第一阶段。生成的区域建议将作为对象查询输入解码器进行进一步细化,形成一个两阶段的可变形DETR。
在第一个阶段,为了实现高召回提议,多尺度特征图中的每个像素将作为一个对象查询。但是,直接将对象查询设置为像素,会给解码器中的自注意模块带来不可接受的计算和内存成本,其复杂度随查询次数的增加呈二次增长。为了避免这个问题,我们删除了解码器,并为区域提议生成形成一个只支持编码器的可变形DETR。在它中,每个像素被分配为一个对象查询,它直接预测一个边界框。选择得分最高的边界框作为区域建议。在将区域建议提交到第二阶段之前,不应用NMS。
5 、EXPERIMENT
6 、CONCLUSION
变形DETR是一种端到端目标检测器,具有高效、快速收敛的特点。它使我们能够探索端到端对象检测器更有趣和实用的变体。可变形DETR的核心是(多尺度)可变形注意模块,它是处理图像特征映射的一种有效的注意机制。我们希望我们的工作为探索端到端对象检测开辟了新的可能性