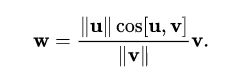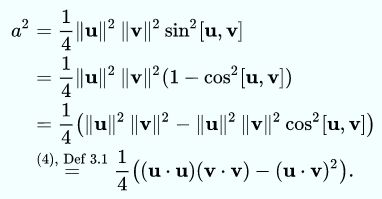向量的点乘（一）

                                        向量的点乘（一）

1.点乘的定义

向量u和向量v之间最小的夹角我们记做为[u,v],如下图所示，两个向量之间的夹角我们用绿色弧形表示，其中一个夹角用绿色矩形表示，这意味着这两个向量的夹角为90度或者是π/2，即[u,v]=π/2。表示这两个向量正交（垂直）。图中左下角表示两个向量0夹角为0，第二行中部表示的是两个向量夹角为π。这两种情况我们都可以称之为共线向量或者平行向量。左下角的两个向量平行且有相同的方向，第二行中部的两个向量平行但是方向相反。

定义1：点乘

向量u和向量v的点乘，表示为u·v，其数值为：

我们知道表示的是向量的长度，由于向量的长度总是一个大于零的标量，那么，对于上述点乘而言，只有当为正数的时候，点乘结果才为正数。因此，我们可以推导出点乘的一些性质：

其中，最后一条性质非常重要。如果两个向量相互正交（垂直），那么他们的点乘。利用这个性质往往能够简化一些计算。

Example ：点乘的简单计算

假设我们有两个向量和。其中向量的长度为4，的长度为3.两个向量的夹角为π/4，任意一个向量都不为零。我们根据上述的定义计算其点乘为：

2.单位向量和归一化

长度为1的向量我们称之为单位向量，也就是说当向量为单位向量，即有。对于任何一个非零向量，我们都可以得到其单位向量。求解单位向量的过程我们称之为归一化。任意一个非零向量，我们可以把该向量除以其长度即可得到归一化的单位向量。即：

3.投影

如下图所示，根据三角学知识，我们知道直角三角形中最小角的余弦可以根据斜边和最短边求得。用表达式可以表示为：

                                                                                            

假设向量正交投影到另外一个向量，得到一个新的向量。如下图所示：

向量和以及虚线构成一个直角三角形。根据三角学的知识可得，，即我们可以得到向量的长度为。如果向量长度为1，即，那么向量可以通过如下式子计算：

                                                                

和相比，我们知道和向量的方向相同，长度正好和的长度一致。上式是针对向量长度为1的情况而言，假设对于任意一个非零向量而言，我们可以通过归一化的方法求得其单位向量，之后再带入到上式中我们即可得到任意非零向量的投影为：

由于向量的归一化并不会改变向量的方向，因此我们任然使用代替。上式中分子分母同乘以标量得到：

根据点乘的定义我们知道，上式的分子正好是点乘。即我们进一步简化为：

因此，我们有正交投影的正式定义为：

对于非零向量，向量正交投影于的投影我们可以定义为：

                                                                                  

上式公式计算出来的是u向量在v向量上与v向量同方向的投影向量w。

向量内积的几何解释就是一个向量在另一个向量上的投影的积，也就是同方向的积。

由于计算出来的向量w和v是同方向的。即

这也就解释了上述内积的几何意义：一个向量在另一个向量投影的积

利用投影的定义，我们可以推到出点乘的一些性质。

点乘的性质：

4.正交基

这一小节我们将介绍一种计算点乘的简单方法。假设我们在三维空间中，以相同的基向量为基础，得到的两个向量和

和。

这两个向量的点乘可以表示为：

展开可得到：

这个式子既长又复杂。但是，但我们假设当时，上式即表示为每一个基向量都正交于另外每一个基向量。我们再进一步假设对所有i都成立。这个等式说明每一个基向量的长度为1.在这两个假设的前提下，上式可以简化为：

 

正交基定义：

对于N维空间的正交基，其中包含一系列基向量，其必然满足：

这意味着，这些基向量都是长度为一的单位向量，且两两相互正交。

正交基中的点乘：

在任何一个正交基中，两个n维向量之间的点乘可以表示为：

例如，在正交基中，二维向量、三维向量之间的点乘可以发分别表示为：

在学校学习线性代数的时候，印象中我们都是直接套用了上述公式。因为默认使用的是以X轴和Y轴为正交基向量的。在校学习的时候只是单纯的知道这么计算，当时也没有深入的思考为什么这样计算。直到多年之后，再次学习到这里，才恍然大悟，原来如此。

Example：

在如下图中的正交基所表示的空间中，，，计算。

我们知道恰好是两个向量的点乘。我们利用其基向量正交的条件可知，

 5.正交基中的向量长度

我们已经知道，在正交基中的向量点乘我们可以简单的通过其坐标点之间的乘积之和求得。在这一小节中，我们也会明白在正交基中，我们也可以简单快速的求得向量的长度。

 

1. 

我们根据点乘的性质知道，。如果v向量在正交基中的坐标为，我们可以根据正交基中的点乘性质知道。如下图所示：

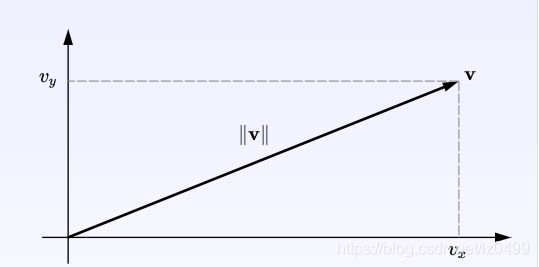
上图中，我们画出了向量，以及它在正交基向量中的坐标。向量在正交基中的表示，类似于下图直角三角形的表示。其中，。我们知道在直角三角形中，根据勾股定理可知：

因此在二维平面中，任意一个在正交基中的向量我们可以通过下式计算其长度：  

6.利用点乘计算三角形的面积

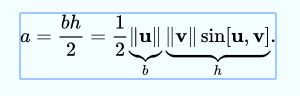
如下图所示，我们用三点定义了一个三角形。我们将利用向量点乘的形式计算其面积。我们将使用两条边构成的向量，。根据三角形知识可知，三角形的面积计算公式为：bh/2,其中b是底边的长度，h是三角形的高。在下图中，,h可以表示为：

 

因此，三角形的面积公式可以转换为：

 

 

由于三角形的面积总为正。我们可以对上式两边开平方可得：

因此，三角形的面积公式向量形式为：

 

 

 

翻译至：http://immersivemath.com/ila/ch03_dotproduct/ch03.html