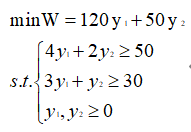运筹说 第30期 | 算法介绍之单纯形法
本期小编继续进行运筹学算法的讲解,我们将介绍对偶单纯形法的平台实现方法,可以快速帮助大家求解线性规划问题,做到事半功倍。话不多说,我们一起来看看吧!
- 一、原理及步骤
1、求解思想
单纯形法求解过程是在保持原始可行的前提下(b保持≥0),通过逐步迭代实现对偶可行(检验数行≤0)。
对偶单纯形法就是换个角度考虑线性规划(Linear programming,简称LP),求解过程:保持对偶可行的前提下(检验数行保持≤0),通过逐步迭代实现原始可行(b列≥0,从非可行解变成可行解)。
2、使用条件
检验数全部≤0
B列至少一个元素﹤0
3、求解步骤
① 列初始单纯形表,检查b列数字:若b列数字均为非负,而检验数行均为非正,则该对偶问题已得到最优解,停止计算;若b列至少还有一个负分量,检验数行保持非正,进行第②步;
② 确定出基变量:选择b列中负值最小者对应变量出基,即 ![]() 对应的
对应的![]() 为出基变量。
为出基变量。
③ 确定进基变量:根据最小比值规则,即以![]() 对应的
对应的![]() 为进基变量,
为进基变量,![]() 为主元素进行迭代。
为主元素进行迭代。
④ 检查是否达到最优:b列非负时达到最优,否则继续②、③步。
4、单纯形法及对偶单纯形法对比
基于本次推文用到的知识点,将单纯形法及对偶单纯形法的区别简单总结如下表所示。
5、对偶单纯形法的优缺点
(1)对偶单纯形法的优点
①不需要人工变量;
②当变量多于约束时,采用对偶单纯形法可以减少迭代次数;
③在灵敏度分析中,某些情况可以用对偶单纯形法处理简化;
(2)对偶单纯形法的缺点
使用对偶单纯形法必须满足两个条件:
①单纯形表中的所有检验数全部≤0;②右端常数项列向量必须有负分量(至少有一个元素<0)。而大多数线性规划问题的初始单纯形表很难满足所有检验数均≤0的要求,因此,对偶单纯形法一般不会单独使用。
- 二、算法实现
我们选取Matlab、Python以及Excel这三个软件对如何实现对偶单纯形法进行讲解,以29期的例题为例,题目如下:
1、Matlab求解
对偶单纯形法算法步骤与单纯形法除了进出基的判断规则不同,其他步骤基本类似,所以小编对第16期推文中介绍的SimplexMax函数稍作修改,得到本期推文中Matlab求解对偶单纯形法算法中的重要函数—DualSimplexMax。
①基本思想:在利用MATLAB平台进行算例测试之前,需要将对偶问题转化为标准形式(同时将y用x替代),具体公式如例题-对偶问题化标准型所示。
②DualSimplexMax函数:
参考哈尔滨商业大学张敬信老师在知乎平台分享的相关资源,在MATLAB编辑器窗口编写求解对偶问题的函数—DualSimplexMax(关注“运筹学”公众号→后台回复“DualSimplexMax”即可获取完整Matlab代码)。
③算例求解:在MATLAB平台命令行窗口输入参数完成算例求解
测试:
运行结果:X为最优解,Z为最优值,ST为求解过程产生的单纯形表。
注意:我们采用Matlab求解时,将对偶问题min(W)化成了标准型max(-W)因此此时求得的是最优解的相反数,最终得到最优解为1350,最优值![]() =5,
=5,![]() =15。
=15。
2、Python求解
除了使用Matlab语言实现对偶单纯形法的求解,我们也可以使用Python语言实现上述过程,此次小编基于上述例题以及CSDN中的文章《单纯形算法及对偶的python实现》为大家介绍求解对偶单纯形法的Python算法,部分代码展示如下(关注“运筹学”公众号→后台回复“Dual simplex”即可获取完整Python代码)。
求解结果
我们采用Python求解时,将对偶问题min(W)化成了标准型max(-W)因此此时求得的是最优解的相反数,最终得到最优解为1350,最优值![]() =5,
=5,![]() =15。
=15。
3、Excel求解
首先我们需要用Excel来加载一个宏,步骤如下:打开Microsoft Excel→文件→选项→加载项→转到→规划求解加载项,在“数据”选项卡中就会出现“规划求解”这一功能,我们用此功能进行求解。
对偶问题:
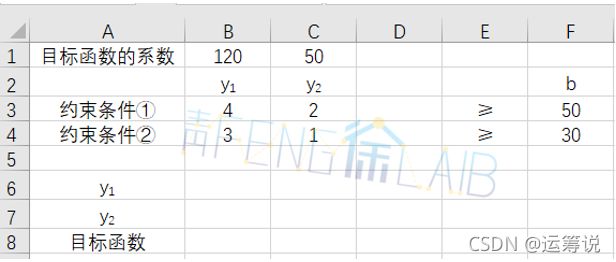
- ①建立Excel工作表
将要求解模型中的每个组成部分放在Excel表格中。用一组单元格表示变量,作为可变单元格(空);用几组单元格分别表示各约束条件和目标函数的系数;用一些单元格输入公式表示各组系数和变量的关系。例题的线性规划模型在表格中可表示为:用单元格B6:B7表示变量![]() 和
和![]() ,用单元格B1:C1表示变量
,用单元格B1:C1表示变量![]() 和
和![]() 在目标函数中的系数,用单元格B3:C4表示变量
在目标函数中的系数,用单元格B3:C4表示变量![]() 和
和![]() 在约束条件中的系数,用单元格D3:D4分别表示两个约束条件的左端项,用单元格F3:F4分别表示两个约束条件的右端项,用单元格B8表示目标函数。
在约束条件中的系数,用单元格D3:D4分别表示两个约束条件的左端项,用单元格F3:F4分别表示两个约束条件的右端项,用单元格B8表示目标函数。
- ②用MMULT函数实现矩阵的相乘:
对于第一个约束条件的左端项![]() 其在单元格中的表示是:D3=MMULT(B4:C4,B7:B8);
其在单元格中的表示是:D3=MMULT(B4:C4,B7:B8);
对于第二个约束条件的左端项![]() 其在单元格中的表示是:D4=MMULT(B5:C5,B7:B8);
其在单元格中的表示是:D4=MMULT(B5:C5,B7:B8);
对于目标函数的约束,其在单元格中的表示是:B8=MMULT(B1:C1,B6:B7)。
- ③用“规划求解”对话框进行求解
将存有目标函数的单元格指定为目标单元格,将表示变量的单元格指定为可变单元格,并建立约束条件。本题中我们在“规划求解参数”对话框中指定B8为目标单元格。由于目标函数是求极小值,因此选中“最小值”。接下来指定B6:B7为可变单元格,然后点击“添加”按钮,就会弹出“添加约束”对话框。在该对话框中,左端输入的是约束条件的左端项,即输入的范围是D3:D4所代表的单元格,右端输入的是约束条件的右端项,即F3:F4所代表的单元格,符号选择“≤”“=”“≥”使得约束条件具体化。如果还需要添加更多的约束条件,可点击“添加”按钮在弹出的新的约束对话框中添加约束;如果没有其他的约束条件需要添加,点击“确定”按钮返回到“规划求解参数”对话框。在“使无约束变量为非负数”前打对勾,并且在选择求解方法时选择“单纯线性规划”,选项选取默认值,然后点击“求解”按钮,就会返回该问题的结果。
可以看到,本题的结果为:![]() =5,
=5,![]() =15,W=1350。
=15,W=1350。
- ④进行求解、生成报告
在“规划求解参数”对话框中按下“求解”按钮,即可求出最优解和最优值。在一般情况下,都会出现如图所示的“规划求解结果”对话框,它显示已经找到了最优解。如果模型无可行解或无最优解,对话框会显示“找不到可行解”或“设定的单元格值未收敛”。
对话框还会生成三个报告:运算结果报告、敏感性报告和极限值报告,选择“运算结果报告”,可以看到详细的结果分析如下:
☆参考资料1:
【运筹学】对偶单纯形法的Matlab实现 - 知乎
☆参考资料2:
单纯形算法及对偶的python实现_陈述c的博客-CSDN博客_python对偶单纯形法
本期的内容就介绍到这里,想要进一步了解运筹学,关注本公众号,快快学起来吧!
作者 | 曹贵玲 尹萌娟
责编 | 何洋洋
审核 | 徐小峰