隐马尔可夫模型学习笔记(一)
隐马尔可夫模型是一个统计模型(指以概率论为基础,采用数学统计方法建立的模型),其主要是应用时序数据建模,比如语音识别、自然语言处理等
要理解隐马尔可夫首先需要梳理几个步骤:
1. 如何理解概念
2. 什么叫转移概率矩阵和生成概率矩阵
3. 模型公式
5. 公式的求解过程
6. python代码串接
一、 如何理解概念
HMM是一个序列问题,我们的问题中要有两类数据,一个是可观测态序列数据 X , 另 一 个 是 不 可 观 测 态 序 列 {{X}},另一个是不可观测态序列 X,另一个是不可观测态序列{{Z}}(也可以说成隐含态序列),在这里,我们首先:假设一,任意时刻的不可观测态只能由上一时刻的不可观测态所决定的,假设二,任意时刻的可观测态只能由当前时刻的不可观测态所决定的。如下图展示:
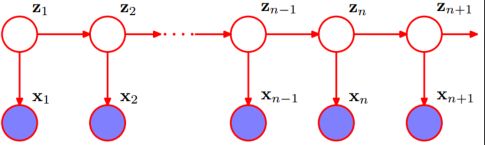
使用一个例子帮忙理解:
掷骰子。假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
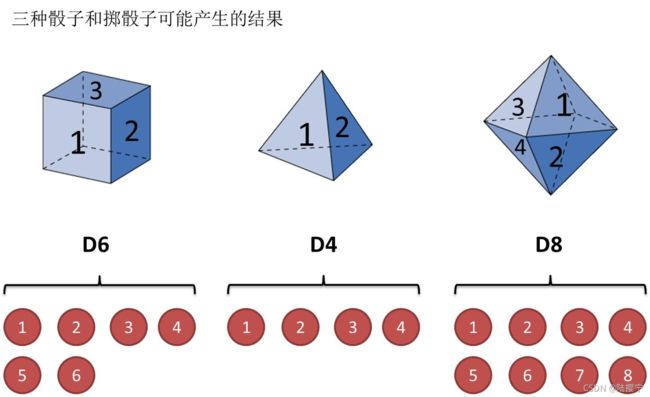
假设我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。然后我们掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。例如我们可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4
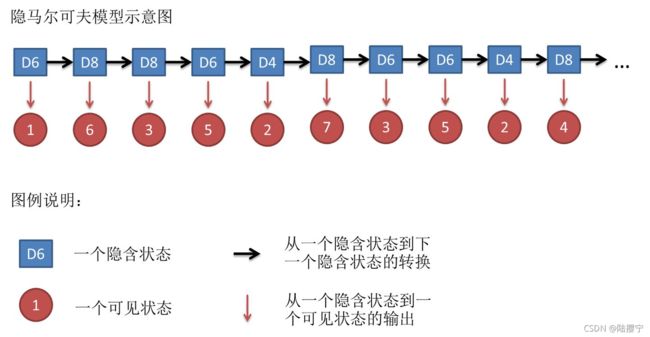
这串数字叫做可见状态链。但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串不可见状态链。在这个例子里,这串不可见状态链就是你用的骰子的序列。比如,不可见状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般来说,HMM中说到的马尔可夫链其实是指不可见状态链,因为不可见状态(骰子)之间存在转换概率(transition probability)。在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是不可见状态和可见状态之间有一个概率叫做输出概率(emission probability)。就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。
二、转移概率矩阵和生成概率矩阵
转移概率矩阵A是指不可观测状态之间的转移概率矩阵,生成概率矩阵B是指可观测状态的生成概率矩阵。
对于HMM模型,首先我们假设是所有可能的不可观测状态的集合,是所有可能的可观测状态的集合,即:
![]()
其中,是可能的不可观察状态数,如上述例子中骰子的类型数,是所有的可能的可观察状态数,如上述例子中显示的骰子的点数;他们是静态的,没有序列概念
对于一个长度为的序列,对应的不可观测状态序列, 是对应的可观测序列即:
![]()
其中,任意一个不可观测状态∈,如上述例子中选择使用的骰子类型的顺序序列;任意一个可观测状态∈,如上述骰出来的点数顺序序列;他们是动态的,从1时刻到T时刻的序列。
1)如果在时刻的隐藏状态是=,在时刻+1的隐藏状态是+1=, 则从时刻到时刻+1的HMM状态转移概率可以表示为:
![]()
这样 a i j a_{ij} aij可以组成马尔科夫链的状态转移矩阵:
![]()
2)如果在时刻的隐藏状态是 = _{}=_{} it=qj, 而对应的观察状态为 = _{}=_{} ot=vk, 则该时刻观察状态 _{} vk在隐藏状态 _{} qj下生成的概率为 ( ) _{}() bj(k),满足:
![]()
这样 ( ) _{}() bj(k)可以组成观测状态生成的概率矩阵:
![]()
三、模型公式
有上面所述,我们知道了状态之间的转化概率。但除此之外,我们需要一组在时刻=1的隐藏状态概率分布 η \mathit{\eta } η:
η = [ π ( i ) ] N \mathit{\eta }=[\pi (i)]_{N} η=[π(i)]N, 其中 π ( i ) = P ( i 1 = q j \pi(i)=P(i_{1}=q_{j} π(i)=P(i1=qj
一个HMM模型,可以由隐藏状态初始概率分布 η \mathit{\eta } η, 状态转移概率矩阵 \mathit{} A和观测状态概率矩阵 B \mathit{B} B决定。 η \mathit{\eta } η , \mathit{} A决定不可观测序列, B \mathit{B} B决定可观测序列。因此,HMM模型可以由一 个三元组 λ \lambda λ表示如下:
![]()
四、公式的求解过程
HMM可以解决的三个基本问题,所以我们从三个问题中求解 λ = ( A , B , η ) \lambda = (A, B,\eta) λ=(A,B,η)公式
1) 评估可观测序列概率。即给定模型 λ = ( A , B , η ) \lambda = (A, B,\eta) λ=(A,B,η)和可观测序列 = 1 , 2 , . . . ={_{1},_{2},..._{}} O=o1,o2,...oT,计算在模型下可观测序列出现的概率(|)。这个问题的求解需要用到前向后向算法,我们在这个系列的第二篇会详细讲解。这个问题是HMM模型三个问题中最简单的。
2)模型参数学习问题。即给定可观测序列 = 1 , 2 , . . . ={_{1},_{2},..._{}} O=o1,o2,...oT,估计模型 λ = ( A , B , η ) \lambda = (A, B,\eta) λ=(A,B,η)的参数,使该模型下可观测序列的条件概率(|)最大。这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法, 我们在这个系列的第三篇会详细讲解。这个问题是HMM模型三个问题中最复杂的。
3)预测问题,也称为解码问题。即给定模型 λ = ( A , B , η ) \lambda = (A, B,\eta) λ=(A,B,η)和可观测序列 = 1 , 2 , . . . ={_{1},_{2},..._{}} O=o1,o2,...oT,求给定可观测序列条件下,最可能出现的对应的不可观测序列,这个问题的求解需要用到基于动态规划的维特比算法,我们在这个系列的第四篇会详细讲解。这个问题是HMM模型三个问题中复杂度居中的算法。
参看资料:
https://www.cnblogs.com/pinard/p/6945257.html
https://www.zhihu.com/question/20962240/answer/33438846