神经网络基础
参考:https://www.bilibili.com/video/BV1XE411C7mS
单节点神经网络
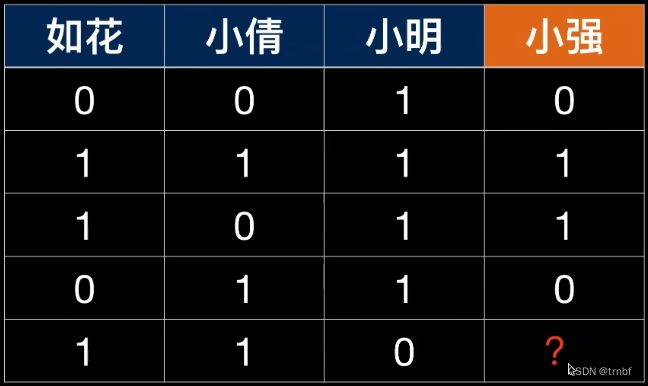
根据前三个人的行为预测小强的行为。
可以明显地看出来,小强的行为只与如花的行为有关。
使用一个单节点的神经网络预测小强的行为,公式就是AW1+BW2+C*W3
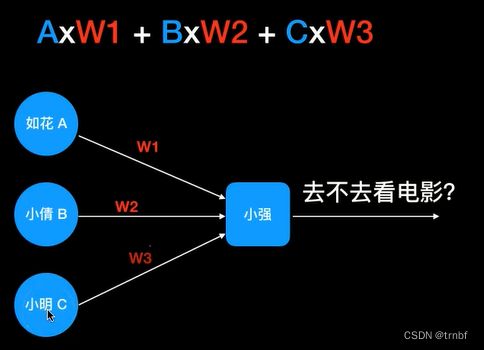
先正向传播,计算出当前权重下得到的结果。
然后反向计算,使用Sigmoid为激活函数,根据误差和斜率来计算增量,不断迭代更新权重矩阵w
from numpy import random, dot, exp, array
#正向传播
#使用Sigmoid为激活函数,使输出在0到1之间,计算出最终的output
def fp(input):
z=dot(input,weights)
return 1/(1+exp(-z))
#反向计算
def bp(y,output):
#计算误差
error=y-output
#计算斜率
slope=output*(1-output)
#计算增量
return error*slope
x=array([[0,0,1],[1,1,1],[1,0,1],[0,1,1]])
y=array([[0,1,1,0]]).T
#设置随机权重,在-1到1之间
random.seed(1)
# weights=2*random.random((3,1))-1
w0=2*random.random((3,4))-1
w1=2*random.random((4,1))-1
for it in range(100000):
output=fp(x)
delta=bp(y,output)
#更新权重
weights=weights+dot(x.T,delta)
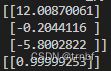
print(weights)
print(fp([[1,1,0]]))
多层神经网络
依旧是根据前三个人的行为预测小强的行为,但是小强的行为逻辑变了。
现在,可以明显地看出来,如花或者大美去,小强就会去;两个人都去,小强就不去了。
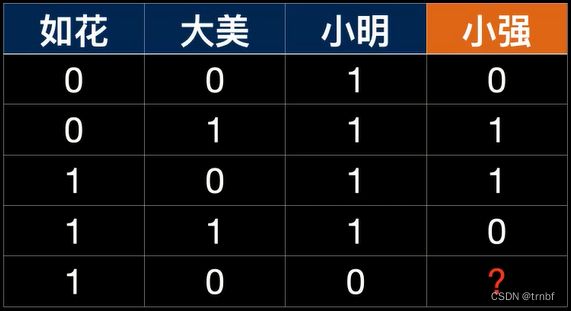
依旧使用单节点神经网络计算,得到的结果是
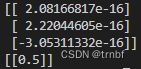
当小强的行为与两个人相关的时候,单节点就失效了。
所以要使用多层的神经网络
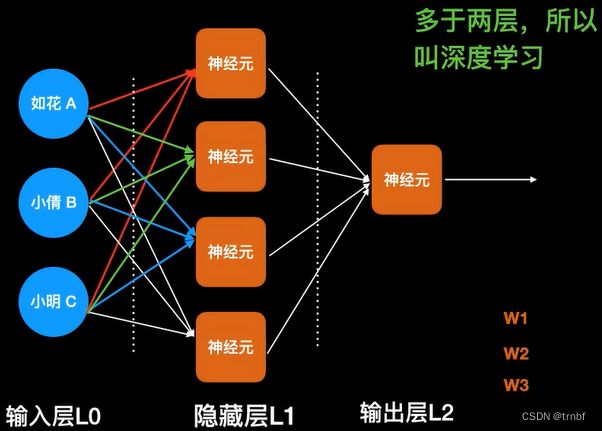
from numpy import random, dot, exp, array
#正向传播
#使用Sigmoid为激活函数,使输出在0到1之间,计算出最终的output
def fp(input):
l1=1/(1+exp(-dot(input,w0)))
l2=1/(1+exp(-dot(l1,w1)))
return l1,l2
#反向计算
def bp(y,l1,l2):
error=y-l2
slope=l2*(1-l2)
l1_delta=error*slope
l0_slope=l1*(1-l1)
l0_error=l1_delta.dot(w1.T)
l0_delta=l0_slope*l0_error
return l0_delta,l1_delta
x=array([[0,0,1],[0,1,1],[1,0,1],[1,1,1]])
y=array([[0,1,1,0]]).T
#设置随机权重,在-1到1之间
random.seed(1)
w0=2*random.random((3,4))-1
w1=2*random.random((4,1))-1
for it in range(100000):
l0=x
l1,l2=fp(l0)
l0_delta,l1_delta=bp(y,l1,l2)
# 更新权重
w0=w0+dot(l0.T,l0_delta)
w1=w1+dot(l1.T,l1_delta)
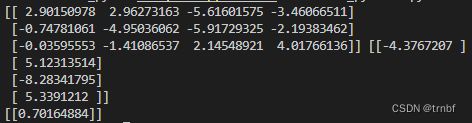
print(w0,w1)
print(fp([[0,0,1]])[1])