基于OP放大器的有源模拟滤波器设计--基础知识

“ 滤波是一个动作，对不同频率的输入信号，实施不同的增益和相移，以形成输出。”

01

—

模拟滤波和数字滤波

滤波这个动作通过通过数字电路或者软件实现的方式就称为数字滤波，其输入量是离散的数字信号，或者是一个程序，对已有的数字序列进行滤波，形成新数据。例如：

原始数据  ,通过以下程序形成  

 这就形成了一个数字滤波的过程，实现了最简单的低通滤波的效果。X序列中存在的尖锐化，会在输出的Y序列中得到钝化 。

同样的滤波这个动作通过模拟电路来实现的方式就称为模拟滤波。

比如我们接下来要介绍的通过OP运放搭建的低通滤波，高通滤波器。只通过纯硬件电路即可实现滤波效果。下面所有的滤波器我们都默认是模拟滤波器。

02

—

电子电路复数表示法

首先是电感：

我们知道，一个线圈就是一个比较简单的电感，而电感有一个特点：当磁场变化时，线圈为了消除磁场变化而使自身产生感应电压，这对应法拉第电磁感应定律：

     ，其中  表示感应电动势，  表示时间， 表示磁通量，  表示电感大小，  表示电流大小。

我们将上式进行变形，令  表示该电感产生的电动势，则：

    化为微分形式就是： 

然后是电容：

我们知道：  ，其中  表示电容内的电荷，  表示电容大小，  表示电容两端的电位差，同时我们知道：  ，因此我们设  表示通过该电容的电流，则：

化为微分形式就是：

接下来，我们首先了解一下复数的基本知识：

在直角坐标系下，复数定义为：  ，其中  ，  称为实部，  称为虚部

在复数中有一个非常著名的公式叫做欧拉公式：

 ，一个简单的证明如下：

对等式左侧进行Maclaurin展开：

利用  这一性质，上式可化为：

而

因此欧拉公式得证

可以注意到，一个复数  ，若将  作为直角坐标系的横轴，  作为直角坐标系的纵轴，那么一个复数可以表示为直角坐标系上的一个向量  ，其与  正半轴的夹角叫做复数的幅角，若设复数的幅角为  ，则 

我们将复数  变换到极坐标系上：

已知：

        

 （这定义为复数的模，或者说是复数在平面直角坐标系上表示时的长度）

那么利用欧拉公式可得： 

我们平常使用的交流电可以定义为： 

其中  表示角频率，  表示初始相角

对于下述电路：

我们根据上面的讨论，很容易列出下列等式：

其中电流  是关于时间  的函数，求解这个方程需要用到高等数学微分方程部分的知识，且求解过程非常复杂。

但是我们可以利用复数轻松求解这个问题：

首先让我们转换一下思想，我们知道一个交流电源包含幅度、角频率及初始相位三个参数，那么我们完全可以用复数的模来表示幅度，复数的幅角来表示角频率及初始相位，因此交流电源电压描述可以变为如下表达式：

 ，其中  ，幅角  ，

根据上述讨论的复数在极坐标下的定义，可以将该表达式改写为：

我们知道上述方程的解一定也是同角频率正弦波（参考高等数学相关微分方程的求解），因此电流类似的改写为：

因此上述微分方程可以简化为：

由于我们只是改变了电压的描述形式，并规定了电流函数解的形式，因此这样代入并不改变上述方程的成立性

我们继续化简：

因此上述方程化简为：

这就是一个简单的代数方程式，而求解该方程中的  的方法我们小学四年级就已经学过了：

同时，我们已知在仅含有电阻  直流电路中，依据欧姆定律可得：  ，其中  为电阻两端的电压，  为电阻两端的电流

类似的，我们在交流电路中引出阻抗的概念，定义为： 

因此，根据上述计算，我们可以很容易得出，电感的感抗为：     类似的，电容的容抗为： 

电阻的阻抗为：     

我们称上面带点的符号为相量，相量具有幅度和相位两个参数，利用相量，我们可以判断交流回路中电压和电流的相位差借此判断相位的超前与滞后现象。

03

—

频率响应

滤波器是依赖于频率基础之上处理信号的一种电路。而随频率变化的这种特性行为称为频率响应，并以传递函数H(jw)表示，这里的  是角频率以弧度/秒（rad/s）计，而j是虚数单位（  ）,这个响应进一步具体为幅度响应  和相位响应；它们分别给出了当信号通过该滤波器后所经受的增益和相移。

04

—

传递函数

滤波器是用其特性和频率相关的器件实现的，如电容器和电感器。当经受交流信号时，这些元件都会以一种依赖于频率的方式反抗电流的变化，并且还在电压和电流之间引入90°的相移。为了考虑这一个特性，采用复阻抗  和 其中式中  是复频率以复奈培/秒(复Np/s)计。这里，  是奈培频率以奈培/秒（Np/s），而  是角频率以弧度/秒（rads/s）计。

一个电路的特性行为位移的由他的传递函数H（s）来表征，为了求得这个函数，首先导出用输入  对输出  的表达式（  和  可以是电压或电流）；这可以利用熟悉的一些方法来做，比如KCL,KVL或者欧姆定律等，然后对这个比值求解

 一旦H（s） 知道，对于某给定的输入  的响应  就能求得为：

 这里  代表拉普拉斯反变换，而  则是  的拉普拉斯变换。

传递函数结果是s的有理函数

 其中N(s)和D(s)是阶次为m和n的，具有实系数的，合适的s多项式，分母的阶决定滤波器的阶次（一阶、二阶等等）。方程N(s)=0和D(s)=0的根分别为H(s)的零点和极点，并用  和  表示，将N(s)和D(s)因式分解成各自的根可写成：

  其中  称为加权因子，除去  外，一旦已知他的零点和极点，H(s)就唯一被确定。由于这些根只与电路有关，也就是只取决于它的元件以及互联方式，而与它的信号或者存贮在电抗性元件中的能量无关，因此这些根也称为临界或者特征频率。事实上，基本的电路特性往往都用这些根来给出。这些根可以是实数或复数。当零点或者极点是复数时，他们以共轭成对出现，例如  是一个极点，那么  也是一个极点。这些根都可以很方便的在复平面进行展现。

H(s)和稳定性

如果一个电路对任何有界输入在响应中产生一个有界的输出就说这个电路是稳定的。判断一个电路是否稳定的一种方法是将某些能量注入到它的电抗元件中的一个或者多个中去，然后再没有任何外加源的情况下观察这个电路本身是如何作为的。在这种情况下的电路相应称为无源或自然响应。注入能量的一种方便的方法是加入一个冲激输入，他的拉普拉斯变换是1。根据上面介绍的拉普拉斯反变换可得

 非常有趣的是这个响应是由极点决定的，现在看看两个有代表性的。

1、H(s)有一个极点  。利用熟知的拉普拉斯变换方法，可以证明H(s)含有  ，这里  称为H(s)在哪个极点的留数，并求得为  =  。由拉普拉斯变换表求得

 式中u(t)是单位阶跃函数（u=0,t<0;u=1,t>0）。一个实数极点对响应  贡献出一个指数分量，而且若  ,这个分量衰减，若  ,保持不变，以及若  ,响应将发散。

2、H(s)有一对复数极点在  ，在这种情况下，H(s)包含复数项  以及他的共轭项，而求得的留数是  。他们组合的拉普拉斯变换是：

 如果  ，这一分量代表一个衰减的正弦；若  ，则代表一个恒定振幅的正弦；以及  ，则代表一幅度增长的正弦。

很清楚，对一个电路要是稳定的话，全部极点都必须位于s平面的左半平面，在哪里有  。无源RLC电路就满足这个条件，因而是稳定的。然而，如果某一电路含有受控源（如运放），那么他的极点就可能落在右半平面，从而会导致不稳定，他的输出会一直增长到运放达到饱和极限为止。如果电路有一对复数极点，输出就是一个持续的振荡。

H(s)和频率响应

在滤波器的研究中，关心的是对如下交流输入

 的响应，这里  是振幅，  是角频率，而  是相角。一般来说，拉普拉斯反变换的完全响应  由两个分量组成，即一个在函数上类似于自然响应的暂态分量，而另一个则是与输入有统一频率但有不同振幅和相角的稳态分量，如果全部极点都位于左半平面LHP，那么暂态分量将最终消逝，而仅有稳态分量

  由于把范围仅缩小到上面这一个分量上，就可以绕过一般的拉普拉斯途径简化数学过程。只要求计算出在虚轴上的H(s)的值，为此求得输出参数为：

    

一般情况下，一个滤波器既影响振幅又影响相角

04

—

伯德图

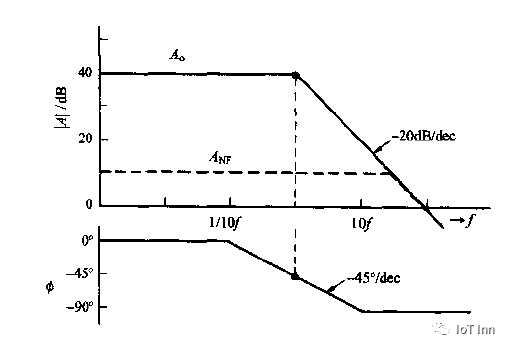
伯德图，也有也翻译成波特图。频率响应的一种可视化展示。可以用手画出来，或者通过各种仿真软件比如pspice,proteus产生。

一个滤波器的幅值和频率范围可能是很宽的，为了用同一清晰度观察小的以及大的细节，幅度和相位分别在对数和半对数标尺上画出。这就是说，频率间隔用每10倍频程（  ,0.01,0.1,1,10,100,  ）或者每倍频程表示(  ),而|H|以分贝（dB）表示为

  伯德图就是分贝和度对10倍频程的图。

听说关注公众号的都是大牛