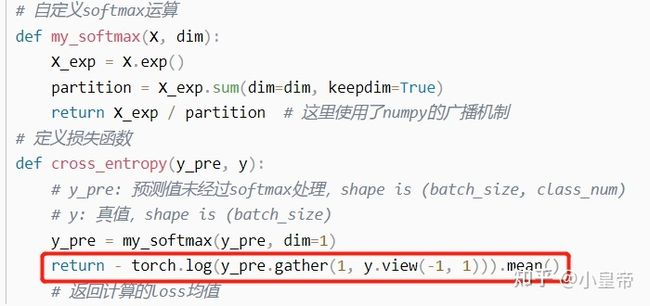
BCE、CE、MSE损失函数

一、BCELoss

代码实现分别提供两种方式：一种是调用官方的nn.BCELoss的API，另一种是自定义函数实现：

# 1、使用API
import torch
import torch.nn as nn
torch.manual_seed(15)
output = torch.randn([2,3])
print("output:","\n",output)
target = torch.tensor([[0,0,1],[1,0,0]],dtype=torch.float32)
print("target:","\n",target)
sigmoid = nn.Sigmoid()
output_sigmoid = sigmoid(output)
print("output_sigmoid:","\n",output_sigmoid)
loss = nn.BCELoss()
bceloss1 = loss(output_sigmoid, target)
print("BCELoss computed by API:","\n",bceloss1)
'''
output: 
 tensor([[-0.7056,  0.6741, -0.5454],
        [ 0.9107,  1.0682,  0.1424]])
target: 
 tensor([[0., 0., 1.],
        [1., 0., 0.]])
output_sigmoid: 
 tensor([[0.3306, 0.6624, 0.3669],
        [0.7131, 0.7443, 0.5355]])
BCELoss computed by API: 
 tensor(0.8264)
'''
# 2、自定义函数
def compute_bce(output_sigmoid, target):
    batch_size = output_sigmoid.shape[0]  # 有几条样本的输出结果
    loss = 0
    for i in range(batch_size):  # 对每条样本
        for j in range(len(output_sigmoid[i])):  # 对每条样本所有类别
            if target[i][j] == 0:
                temp_loss = torch.log(1-output_sigmoid[i][j])
            else:
                temp_loss = torch.log(output_sigmoid[i][j])
            loss = loss - temp_loss
    return loss/(batch_size * output_sigmoid.shape[1])
bceloss2 = compute_bce(output_sigmoid, target) 
bceloss2    
# tensor(0.8264)

二、CELoss

CE的计算过程这样描述：网络的输出，假定为2*3，也就是两条，每条里面三个数，具体意思为batch_size=2，num_class=3。对每一个样本的网络输出先做softmax处理，然后所有数值取log，然后将标签对应位置的值加起来，再对样本数量做平均。

官方的API实现方式为：

import torch
import torch.nn as nn
torch.manual_seed(15)
output = torch.randn([2,3])
target = torch.tensor([2,0])
loss = nn.CrossEntropyLoss()
celoss1 = loss(output, target)
celoss1
# tensor(1.3122)

自定义函数方式实现方式为：

也可以按照下面的方式实现(和BCE一样的形式)：

import torch
import torch.nn as nn
torch.manual_seed(15)
output = torch.randn([2,3])
target = torch.tensor([[0,0,1],[1,0,0]],dtype=torch.float32)
def my_softmax(output):
    output_exp = torch.exp(output)
    partition = output_exp.sum(dim=1, keepdim=True)
    output_exp_softmax = output_exp / partition
    return output_exp_softmax
def compute_ce(output, target):
    output_exp_softmax = my_softmax(output)
    output_exp_softmax_log = torch.log(output_exp_softmax)
    loss = 0
    for i in range(output.shape[0]):
        for j in range(len(output[i])):
            if target[i][j] == 0:
                pass
            else:
                loss = -1 * output_exp_softmax_log[i][j] + loss
    return loss / output.shape[0]
celoss2 = compute_ce(output, target)
celoss2
# tensor(1.3122)

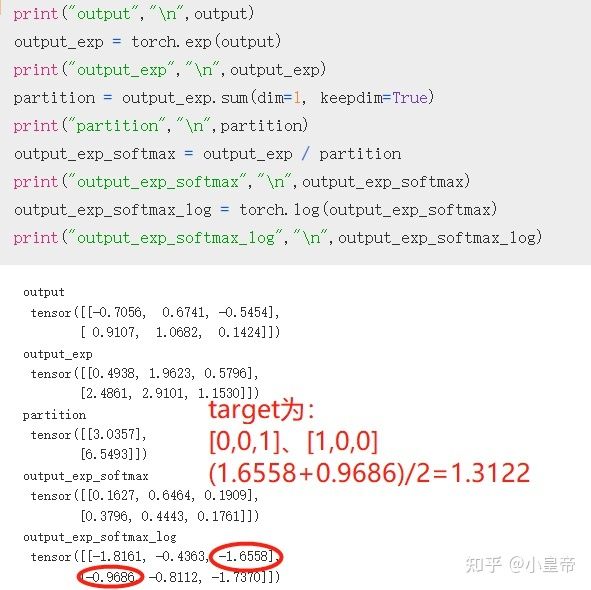
使用方式为CELoss+softmax，由下图推导过程可以看到，当输出结果离标签较远时，梯度比较大，网络修正幅度较大；当输出结果很接近于标签时，梯度接近于0，网络接近稳定，这是我们希望的情况。

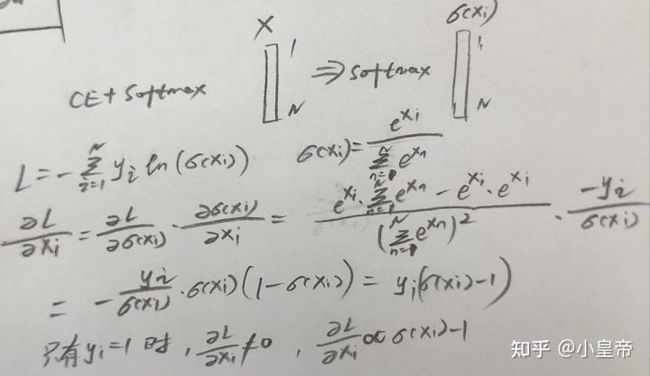
三、MSE

MSE：mean squared error (squared L2 norm)均方误差

MSE与CE相比，MSE不能处理分类问题，因为会出现梯度消失的情况。具体推导如下所示：

CELoss使用的是softmax的输出结果，当使用MSE做loss时对节点权重求偏导，结果中存在一个与输出有关的独立项(蓝色圈)，当网络输出结果与标签较远的时候，这一项接近于0，而这时我们本来是希望有较大的梯度使得网络快速修正节点参数的，显然这时产生的梯度消失是不利的，因为MSE是不适合处理分类问题的。而同样的处理方式来看CELoss对于节点参数的偏导，不存在这样的与输出有关的独立项，因而梯度和网络输出结果有正确的关系，可以完成分类任务。

接下来说说，MSE作为回归损失的情况：

先说结论：MAE-L1 Loss对异常点的鲁棒性更好。
MAE-L1 Loss相当于做中值回归，MSE-L2 Loss相当于做均值回归，这要如何理解呢？如下：

可见，这是从损失的偏导数的角度来看的，考虑的是估计量为什么的时候才能让偏导数等于0，相当于是最大似然估计。关于MSE和MAE的优缺点比较以及修正方法(huber损失函数)在这里面：
机器学习中的损失函数(二) 回归问题的损失函数

Huber损失函数的在误差较小的时候是MSE，误差较大的时候是MAE，因此它可以保证对敏感值鲁棒的同时又能使得梯度随着损失减小而减小从而尽量不错过最优解。