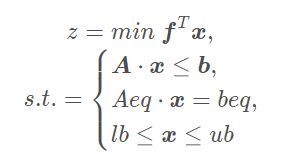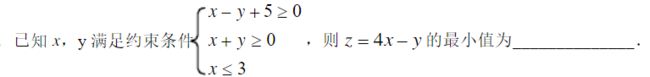用python解决线性规划
这是线性规划的标准型:
这么看未免有些抽象,我们将在代码中逐步了解
先导入库函数:
from scipy import optimize
import numpy as np
之后,范围限定,注意,系统默认是小于等于且求最小值,所以一切大于等于的不等式都要在两边同时乘以-1:
c = np.array([4,-1]) #导入向量,因为是4x-y,所以是【4,-1】
A = np.array([[-1,1],[-1,-1]]) #不等式变为小于等于后,不等式左边的向量
b = np.array([5,0]) #将系数移至右边时,右边的向量
x=(None,3) #规定x的范围
y=(None,None) #规定y的范围
最后就是求解啦:
res = optimize.linprog(c,A,b,bounds=(x,y)) #这里就是直接按照引用函数的标准来啦
print(res)
综上,完整代码如下:
from scipy import optimize
import numpy as np
c = np.array([4, -1])
A = np.array([[-1, 1], [-1, -1]])
b = np.array([5, 0])
x = (None, 3)
y = (None, None)
res = optimize.linprog(c, A, b, bounds=(x, y))
print(res)
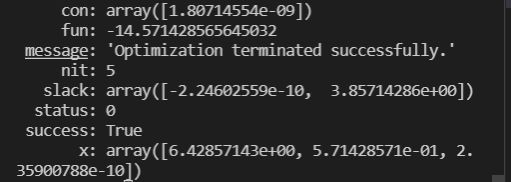
我们可以得到结果:
fun就是所求结果,而x:array()就是x的取值
2.我们再来看一个更复杂的题目,这里的限制条件多了等式:
有了之前的基础,这次直接放完整代码,题目中等式的约束对应的就是代码中的Aeq,beq:
from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
b = np.array([-10,12])
Aeq = np.array([[1,1,1]])
beq = np.array([7])
x1 = (0,None)
x2 = (0,None)
x3 = (0,None)
res=optimize.linprog(-c,A,b,Aeq,beq,bounds=(x1,x2,x3))
print(res)可以得到结果:
一定要注意,系统默认的都是小于等于的条件和求最小值,所以最后求最大值的时候输出的是-c
3.在数学建模解线性规划问题时,更常用到的方法是调包pulp库,大多数人认为它更方便且功能更强大,我们来看看如何使用吧:
仍然是这一个题
首先,导入pulp库并定义线性规划问题:
import pulp
Myproblem = pulp.LpProblem(sense=pulp.LpMaximize)之后,定义变量:
x1 = pulp.LpVariable('x1',lowBound=0,upBound=None,cat='Continuous')
x2 = pulp.LpVariable('x2',lowBound=0,upBound=None,cat='Continuous')
x3 = pulp.LpVariable('x3',lowBound=0,upBound=None,cat='Continuous')lowBound定义下界,upBound定义上界,cat设定变量类型,Continuous是连续型,Integer是离散型,Binary表示0/1变量
接下来,定义变量的范围,标准格式是‘问题名 += 约束条件表达式’:
Myproblem += 2*x1+3*x2-5*x3
Myproblem +=(x1+x2+x3==7)
Myproblem +=(2*x1-5*x2+x3>=10)
Myproblem +=(x1+3*x2+x3<=12)
最后就是求解啦~:
Myproblem.solve()
for i in Myproblem.variables():
print(i.name,'=',i.varValue)
print('F(x)=',pulp.value(Myproblem.objective))完整的代码:
import pulp
Myproblem = pulp.LpProblem(sense=pulp.LpMaximize)
x1 = pulp.LpVariable('x1',lowBound=0,upBound=None,cat='Continuous')
x2 = pulp.LpVariable('x2',lowBound=0,upBound=None,cat='Continuous')
x3 = pulp.LpVariable('x3',lowBound=0,upBound=None,cat='Continuous')
Myproblem += 2*x1+3*x2-5*x3
Myproblem +=(x1+x2+x3==7)
Myproblem +=(2*x1-5*x2+x3>=10)
Myproblem +=(x1+3*x2+x3<=12)
Myproblem.solve()
for i in Myproblem.variables():
print(i.name,'=',i.varValue)
print('F(x)=',pulp.value(Myproblem.objective))得到的结果是:
结果的表示是不是非常清晰,非常明了哈哈~
ps:如果有哪儿写的不太清楚欢迎留言,我会即使改进,如果哪儿写的有问题也欢迎指正