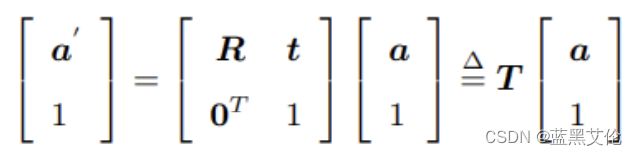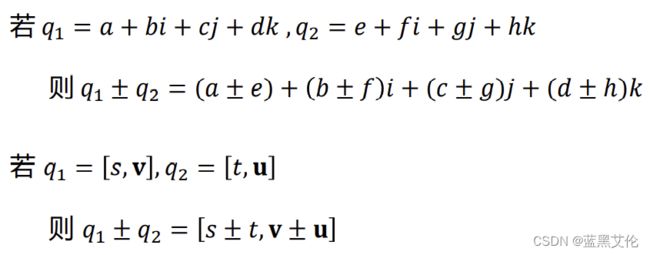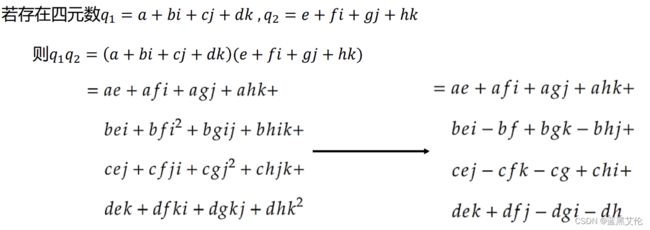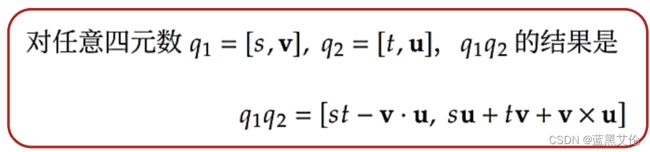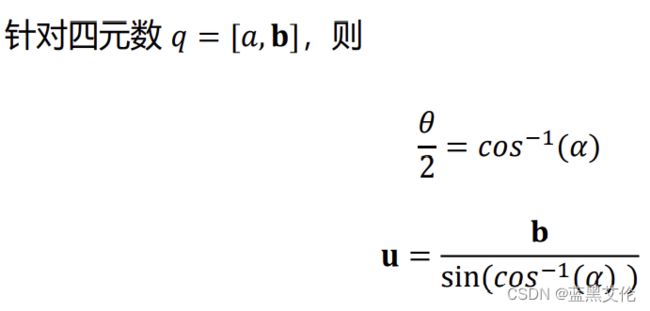SLAM学习笔记4：三维空间刚体运动

导引：

        我们在笔记2中提到了SLAM问题的基本方程，它由运动方程和观测方程组成。接下来我们要讨论的就是运动方程。

        运动方程用来表述传感器的位姿变化。所谓“位姿”，包含位置和姿态两方面。表述位姿变化的问题就是描述刚体在三维空间中的运动。

        刚体的三维空间运动（对应于“位姿变化”）可以分解为平移运动（对应于“位置变化”）和旋转运动（对应于“姿态变化”）：

        平移运动表述的是刚体位置的变化，可以用向量的加减运算来表示。 旋转运动表述的是刚体姿态的变化，可以用旋转矩阵、旋转向量或者四元数来表示。

一、旋转矩阵、变换矩阵和齐次坐标：

1.欧氏变换与旋转矩阵：

（1）两个坐标系及其转换：

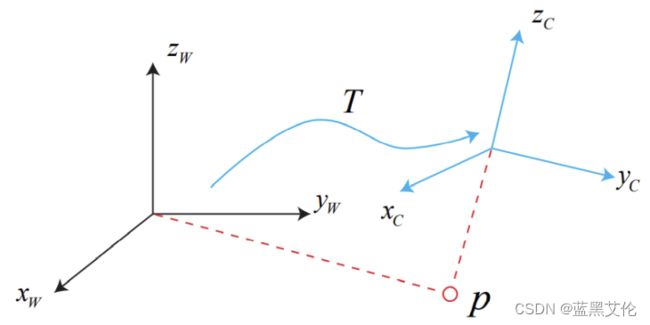
        在描述刚体的三维运动时，常见的做法是设置两个坐标系：惯性坐标系（世界坐标系）和移动坐标系。

        认为惯性坐标系是静止不动的，相机或机器人是移动坐标系。

        对于向量 ：在世界坐标系下其坐标为；相机视野下，其坐标为。为了转换这两个坐标，要先得到该点针对移动坐标系的坐标值，再根据机器人位姿变换到世界坐标系中。这种变换需要用一个矩阵T来描述。

（2）刚体运动：

        两个坐标系之间的运动由一个旋转和一个平移组成，这种运动称为刚体运动。刚体运动过程中，同一个向量在各个坐标系下的长度和夹角都不会发生变化，仅相差了一个欧式变换。

（3）欧氏变换与旋转矩阵：

        坐标系间的欧氏变换由一次平移和一次旋转组成。

 

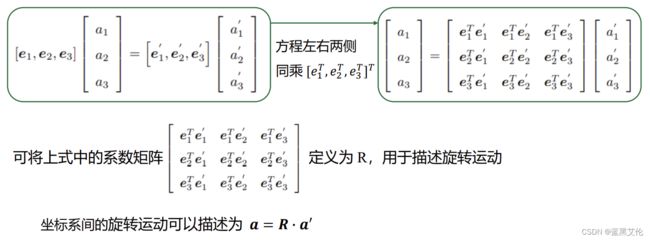
        这个矩阵R就是旋转矩阵，它由两组基之间的内积组成，刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的，这个矩阵就是一样的。

        由于基向量的长度为1，所以实际上是各基向量夹角的余弦值，因此该矩阵也称为方向余弦矩阵。

（4）旋转矩阵的性质：

        旋转矩阵是行列式为1的正交矩阵；反之，行列式为1的正交矩阵也是一个旋转矩阵（充要条件）。

（5）特殊正交群：

        群的概念会在之后的笔记6中提到。

（6）旋转矩阵的逆：

        旋转矩阵的逆（即转置）描述了一个相反的旋转。 

 

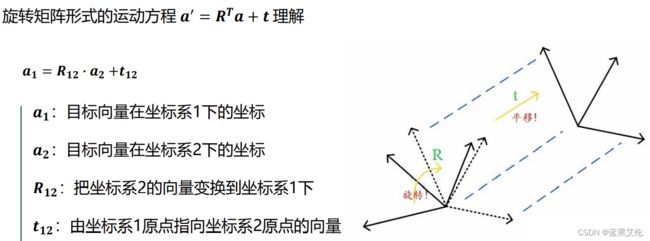
（7）旋转矩阵形式的运动方程：

        R是旋转向量，描述一次旋转；t是平移向量，描述一次平移。 

2.变换矩阵和齐次坐标：

（1）旋转矩阵形式的运动方程的缺点：

        旋转矩阵形式的运动方程的变换不是线性关系，在连续变换多次后形式会非常复杂。

        为了简化运算，引入齐次坐标和变换矩阵。

（2）齐次坐标：

        在三维向量的末尾添加一个1，使其变为四维向量，称为齐次坐标。 

（3）变换矩阵：

 

        同样地，变换矩阵的逆表示与其相反的变换：

 

（4）变换矩阵的结构特征：

        左上角为旋转矩阵，右侧为平移向量，左下角为零向量，右下角为1。

（5）变换矩阵形式的运动方程：

 

（6）特殊欧氏群：

 

二、旋转向量和欧拉角：

1.矩阵表示方式的缺点：

（1）SO(3) 的旋转矩阵有 9 个量，但只用于描述 3 个自由度的运动；

（2）SE(3) 的变换矩阵有 16 个量，但只用于描述 6 个自由度的运动。

        这说明矩阵表示方式不够紧凑，造成了运算空间的浪费。此外，旋转矩阵必须是正交矩阵且行列式为1，变换矩阵同样具有对应的要求，这些约束会给优化与求解造成困难。因此需要寻找一种更简洁紧凑的表示法。

2.旋转向量：

（1）旋转向量的定义：

        一个向量，其方向与旋转轴一致，而长度等于旋转角，这种向量称为旋转向量。

 

（2）旋转向量到旋转矩阵的转换过程：

        从旋转向量到旋转矩阵的转换过程由罗德里格斯公式表明，推导过程较为复杂，这里不做描述，只给出转换结果：

（3） 旋转矩阵到旋转向量的转换过程：

 

3.欧拉角：

（1）什么是欧拉角：

        相较于旋转矩阵和旋转向量这种不太直观的描述旋转的方式，欧拉角显得非常直观：使用3个分离的转角，将一个旋转分解成3次绕不同轴的旋转。

（2）常用的欧拉角定义：

        “偏航 – 俯仰 – 滚转”(yaw-pitch-roll) （X轴指向刚体前方，Y轴指向右侧，Z轴指向上方）

1）绕物体 Z 轴旋转，得到偏航角 yaw

2）绕旋转之后 的 Y 轴旋转，得到俯仰角 pitch

3）绕旋转之后 的 X 轴旋转，得到滚转角 roll

（3）欧拉角的缺点（万向锁问题，了解）：

        在俯仰角为±90°时，第一次旋转与第三次转转将使用同一个轴，使得系统丢失了一个自由度（由3次旋转变成2次旋转）

三、四元数：

1.为什么引入四元数概念：

（1）旋转矩阵用9个量描述3个自由度，具有冗余性；

（2）旋转向量和欧拉角是紧凑的，但具有奇异性，事实上也找不到不带奇异性的三维向量描述方式。

        在表达三维旋转时，有一种类似于复数（复数集可用来表示复平面上的向量）的代数：四元数。它既是紧凑的，也没有奇异性，少有的缺点是不够直观、运算稍复杂。

2.四元数的定义：

（1）四元数的表示方法：

1）

 

2）

 

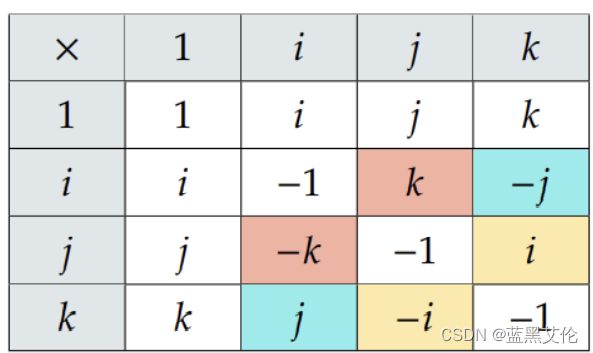
（2）i,j,k三者间的运算关系：

 

3.四元数的运算：

（1）加法和减法：

 

（2）数乘：

 

（3）模长：

（4）共轭：

 

（5）逆：

 

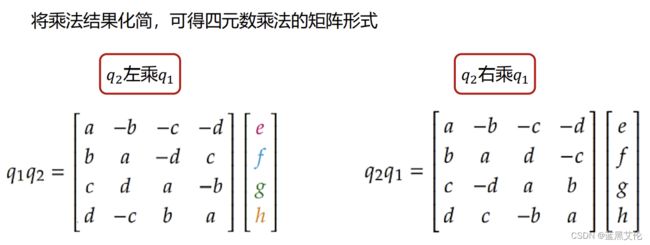
（6）乘法：

 

 

（7）纯四元数：

 

4.用四元数表示三维旋转：

        （推导过程略）

 

5.四元数与旋转向量的变换：