有亿点点烧脑的粗糙集属性约简----4 模糊自信息测度及其特征选择应用
模糊自信息测度及其特征选择应用
- 1 模糊自信息及相关性质
-
- 1.1 安全决策自信息
- 1.2 风险决策自信息
- 1.3 安全-风险决策自信息
- 1.4 相对决策自信息
- 2 应用举例
- 3 小结
- 参考文献
模糊自信息可以表示信号的不确定性。将自信息的概念引出到模糊粗糙集模型中可以用来度量模糊决策的不确定性。
1 模糊自信息及相关性质
定义 1.1 测度 I ( x ) I(x) I(x) 是由 Claude Shannon 提出的,表示信号 x x x 的不确定性,称 I ( x ) I(x) I(x) 是 x x x 的自信息,如果满足如下条件:
(1) 非负性: I ( x ) ≥ 0 I(x) \geq 0 I(x)≥0;
(2) 如果 p ( x ) → 0 p(x) \rightarrow 0 p(x)→0,则有 I ( x ) → ∞ I(x) \rightarrow \infty I(x)→∞;
(3) 如果 p ( x ) = 1 p(x)=1 p(x)=1,则有 I ( x ) = 0 I(x)=0 I(x)=0;
(4) 严格单调性: 如果 p ( x ) > p ( y ) p(x)>p(y) p(x)>p(y),则有 I ( x ) < I ( y ) I(x)
这里 p ( x ) p(x) p(x) 是 x x x 出现的概率。
定义 1.2 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ , D r } , R A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots, D_{r}\right\}, R_{A} (U,A,D),U/D={D1,D2,⋯,Dr},RA 是由 A A A 诱导的 U U U 上 的模糊相似关系,对于任意的 x ∈ U x \in U x∈U,样本 x x x 的模糊决策 D ~ i ( x ) \widetilde{D}_{i}(x) D i(x) 定义如下:
D ~ i ( x ) = ∣ [ x ] A ∩ D i ∣ [ x ] A . \widetilde{D}_{i}(x)=\frac{\left|[x]_{A} \cap D_{i}\right|}{[x]_{A}}. D i(x)=[x]A∣[x]A∩Di∣.
定义 1.3 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ , D r } , { D ~ 1 , D ~ 2 , ⋯ , D ~ r } (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots, D_{r}\right\},\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \widetilde{D}_{r}\right\} (U,A,D),U/D={D1,D2,⋯,Dr},{D 1,D 2,⋯,D r} 是相 对于 U / D U / D U/D 的模糊划分, A = { a 1 , a 2 , ⋯ , a m } A=\left\{a_{1}, a_{2}, \cdots, a_{m}\right\} A={a1,a2,⋯,am} 是真值属性集, B ⊆ A , R B B \subseteq A, R_{B} B⊆A,RB 是由 B B B 诱导的 U U U 上的模糊相似关系,对于任意 D i ∈ U / D , D i D_{i} \in U / D, D_{i} Di∈U/D,Di 的模糊下近似和上近似定义如下:
R ‾ B ( D i ) ( x ) = inf y ∈ U max { 1 − R B ( x , y ) , D ~ i ( y ) } , x ∈ U , R ˉ B ( D i ) ( x ) = max y ∈ U inf { R B ( x , y ) , D ~ i ( y ) } , x ∈ U . \begin{gathered} \underline{R}_{B}\left(D_{i}\right)(x)=\inf _{y \in U} \max \left\{1-R_{B}(x, y), \widetilde{D}_{i}(y)\right\}, \quad x \in U, \\ \quad \bar{R}_{B}\left(D_{i}\right)(x)=\max _{y \in U} \inf \left\{R_{B}(x, y), \widetilde{D}_{i}(y)\right\}, \quad x \in U. \end{gathered} RB(Di)(x)=y∈Uinfmax{1−RB(x,y),D i(y)},x∈U,RˉB(Di)(x)=y∈Umaxinf{RB(x,y),D i(y)},x∈U.
定义 1.4 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ , D r } , B ⊆ A , R B (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots, D_{r}\right\}, \quad B \subseteq A, R_{B} (U,A,D),U/D={D1,D2,⋯,Dr},B⊆A,RB 是由 B B B 诱 导的 U U U 上的模糊相似关系,相对于属性子集 B B B,模糊决策 D i D_{i} Di 的决策指标 S ( D i ) S\left(D_{i}\right) S(Di),安全决策指标 l o w e r S B ( D i ) lowerS_{B}\left(D_{i}\right) lowerSB(Di),风险决策指标 u p p e r S B ( D i ) upperS_{B}\left(D_{i}\right) upperSB(Di) 定义如下:
S ( D i ) = 1 n ∑ j = 1 n D ~ i ( x j ) , l o w e r S B ( D i ) = 1 n ∑ j = 1 n R ‾ B ( D i ) ( x j ) , u p p e r S B ( D i ) = 1 n ∑ j = 1 n R ˉ B ( D i ) ( x j ) . \begin{gathered} S\left(D_{i}\right)=\frac{1}{n} \sum_{j=1}^{n} \widetilde{D}_{i}\left(x_{j}\right), \\ lower S_{B}\left(D_{i}\right)=\frac{1}{n} \sum_{j=1}^{n} \underline{R}_{B}\left(D_{i}\right)\left(x_{j}\right), \\ upperS_{B}\left(D_{i}\right)=\frac{1}{n} \sum_{j=1}^{n} \bar{R}_{B}\left(D_{i}\right)\left(x_{j}\right). \end{gathered} S(Di)=n1j=1∑nD i(xj),lowerSB(Di)=n1j=1∑nRB(Di)(xj),upperSB(Di)=n1j=1∑nRˉB(Di)(xj). 安全决策指标表示样本被一致地分类为决策类的信息,风险决策指标表示样本可能属于该决策类的信息。
1.1 安全决策自信息
定义 1.5 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A, 相对于 B B B ,决策 D i D_{i} Di 的安全决策精度 α B ( 1 ) ( D i ) \alpha_{B}^{(1)}\left(D_{i}\right) αB(1)(Di) 和安全决策粗糙度 β B ( 1 ) ( D i ) \beta_{B}^{(1)}\left(D_{i}\right) βB(1)(Di) 定义如下:
α B ( 1 ) ( D i ) = l o w e r S B ( D i ) S ( D i ) , β B ( 1 ) ( D i ) = 1 − α B ( 1 ) ( D i ) . \begin{aligned} &\alpha_{B}^{(1)}\left(D_{i}\right)=\frac{{lower} S_{B}\left(D_{i}\right)}{S\left(D_{i}\right)}, \\ &\beta_{B}^{(1)}\left(D_{i}\right)=1-\alpha_{B}^{(1)}\left(D_{i}\right). \end{aligned} αB(1)(Di)=S(Di)lowerSB(Di),βB(1)(Di)=1−αB(1)(Di). 显然, 0 ≤ α B ( 1 ) ( D i ) ≤ 1 , 0 ≤ β B ( 1 ) ≤ 1. α B ( 1 ) ( D i ) 0 \leq \alpha_{B}^{(1)}\left(D_{i}\right) \leq 1,0 \leq \beta_{B}^{(1)} \leq 1 . \alpha_{B}^{(1)}\left(D_{i}\right) 0≤αB(1)(Di)≤1,0≤βB(1)≤1.αB(1)(Di) 表示特征子集 B B B 具有一致分类能力的程度。 β B ( 1 ) ( D i ) \beta_{B}^{(1)}\left(D_{i}\right) βB(1)(Di) 表示样本无法完全正确分组到决策类 D i D_{i} Di 的程度。
定义 1.6 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A,安全决策自信息定义如下:
I B ( 1 ) ( D i ) = − β B ( 1 ) ( D i ) log α B ( 1 ) ( D i ) . I_{B}^{(1)}\left(D_{i}\right)=-\beta_{B}^{(1)}\left(D_{i}\right) \log \alpha_{B}^{(1)}\left(D_{i}\right). IB(1)(Di)=−βB(1)(Di)logαB(1)(Di).
定义 1.7 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A, 决策表的安全决策自信息定义如下:
I B ( 1 ) ( D ) = ∑ i = 1 r I B ( 1 ) ( D i ) . I_{B}^{(1)}(D)=\sum_{i=1}^{r} I_{B}^{(1)}\left(D_{i}\right). IB(1)(D)=i=1∑rIB(1)(Di).
定义 1.8 给定决策表 ( U , A , D ) , B ⊆ A (U, A, D), B \subseteq A (U,A,D),B⊆A, 称 B B B 为相对于决策 D , A D, A D,A 的一个安全决策约简,如果满足如下条件:
(1) I B ( 1 ) ( D ) = I A ( 1 ) ( D ) I_{B}^{(1)}(D)=I_{A}^{(1)}(D) IB(1)(D)=IA(1)(D);
(2) I B − { a } ( 1 ) ( D ) ≠ I B ( 1 ) ( D ) I_{B-\{a\}}^{(1)}(D) \neq I_{B}^{(1)}(D) IB−{a}(1)(D)=IB(1)(D), 对于任意 a ∈ B a \in B a∈B.
1.2 风险决策自信息
定义 1.9 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A,相对于 B B B,决策 D i D_{i} Di 的风险决策精度 α B ( 2 ) ( D i ) \alpha_{B}^{(2)}\left(D_{i}\right) αB(2)(Di) 和风险决策粗糙度 β B ( 2 ) ( D i ) \beta_{B}^{(2)}\left(D_{i}\right) βB(2)(Di) 的定义如下:
α B ( 2 ) ( D i ) = S ( D i ) u p p e r S B ( D i ) , β B ( 2 ) ( D i ) = 1 − α B ( 2 ) ( D i ) . \begin{gathered} \alpha_{B}^{(2)}\left(D_{i}\right)=\frac{S\left(D_{i}\right)}{upper S_{B}\left(D_{i}\right)}, \\ \beta_{B}^{(2)}\left(D_{i}\right)=1-\alpha_{B}^{(2)}\left(D_{i}\right). \end{gathered} αB(2)(Di)=upperSB(Di)S(Di),βB(2)(Di)=1−αB(2)(Di). 显然, 0 < α B ( 2 ) ( D i ) ≤ 1 0<\alpha_{B}^{(2)}\left(D_{i}\right) \leq 1 0<αB(2)(Di)≤1 且 0 ≤ β B ( 2 ) < 1. 0 \leq \beta_{B}^{(2)}<1 . 0≤βB(2)<1. 这里 α B ( 2 ) ( D i ) \alpha_{B}^{(2)}\left(D_{i}\right) αB(2)(Di) 表示特征子集 B B B 刻画风险决策分类的能力, β B ( 2 ) ( D i ) \beta_{B}^{(2)}\left(D_{i}\right) βB(2)(Di) 表示样本无法正确分组到决策类 D i D_{i} Di 的程度。
定义 1.10 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A, 风险决策自信息定义如下:
I B ( 2 ) ( D i ) = − β B ( 2 ) ( D i ) log α B ( 2 ) ( D i ) . I_{B}^{(2)}\left(D_{i}\right)=-\beta_{B}^{(2)}\left(D_{i}\right) \log \alpha_{B}^{(2)}\left(D_{i}\right). IB(2)(Di)=−βB(2)(Di)logαB(2)(Di).
定义 1.11 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A, 决策表的风险决策自信息定义如下:
I B ( 2 ) ( D ) = ∑ i = 1 r I B ( 2 ) ( D i ) . I_{B}^{(2)}(D)=\sum_{i=1}^{r} I_{B}^{(2)}\left(D_{i}\right). IB(2)(D)=i=1∑rIB(2)(Di).
1.3 安全-风险决策自信息
定义 1.12 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A,安全-风险决策自信息定义如下:
I B ( 3 ) ( D i ) = I B ( 1 ) ( D i ) + I B ( 2 ) ( D i ) . I_{B}^{(3)}\left(D_{i}\right)=I_{B}^{(1)}\left(D_{i}\right)+I_{B}^{(2)}\left(D_{i}\right). IB(3)(Di)=IB(1)(Di)+IB(2)(Di).
定义 1.13 定义 4.1.12 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A,决策表的安全-风险决策自信息定义如下:
I B ( 3 ) ( D ) = ∑ i = 1 r I B ( 3 ) ( D i ) . I_{B}^{(3)}(D)=\sum_{i=1}^{r} I_{B}^{(3)}\left(D_{i}\right). IB(3)(D)=i=1∑rIB(3)(Di).
1.4 相对决策自信息
定义 1.14 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A,相对于 B B B 的决策 D i D_{i} Di 的相对决策精度 α B ( 3 ) ( D i ) \alpha_{B}^{(3)}\left(D_{i}\right) αB(3)(Di) 和相对决策粗糙度 β B ( 3 ) ( D i ) \beta_{B}^{(3)}\left(D_{i}\right) βB(3)(Di) 的定义如下:
α B ( 3 ) ( D i ) = l o w e r S B ( D i ) u p p e r S B ( D i ) , β B ( 3 ) ( D i ) = 1 − α B ( 3 ) ( D i ) . \begin{gathered} \alpha_{B}^{(3)}\left(D_{i}\right)=\frac{{lower} S_{B}\left(D_{i}\right)}{{upperS}_{B}\left(D_{i}\right)}, \\ \beta_{B}^{(3)}\left(D_{i}\right)=1-\alpha_{B}^{(3)}\left(D_{i}\right). \end{gathered} αB(3)(Di)=upperSB(Di)lowerSB(Di),βB(3)(Di)=1−αB(3)(Di). 显然, 0 ≤ α B ( 3 ) ( D i ) ≤ 1 , 0 ≤ β B ( 3 ) ≤ 1. α B ( 3 ) ( D i ) 0 \leq \alpha_{B}^{(3)}\left(D_{i}\right) \leq 1,0 \leq \beta_{B}^{(3)} \leq 1 . \alpha_{B}^{(3)}\left(D_{i}\right) 0≤αB(3)(Di)≤1,0≤βB(3)≤1.αB(3)(Di) 表示特征子集 B B B 相对于风险决策的描述安全决策分类的能力, β B ( 3 ) ( D i ) \beta_{B}^{(3)}\left(D_{i}\right) βB(3)(Di) 反映了将样本分组为 D i D_{i} Di 的分类能力的不确定性。
定义 1.15 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ D r } , B ⊆ A (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots D_{r}\right\}, B \subseteq A (U,A,D),U/D={D1,D2,⋯Dr},B⊆A, 相对决策自信息定义如下:
I B ( 4 ) ( D i ) = − β B ( 3 ) ( D i ) log α B ( 3 ) ( D i ) . I_{B}^{(4)}\left(D_{i}\right)=-\beta_{B}^{(3)}\left(D_{i}\right) \log \alpha_{B}^{(3)}\left(D_{i}\right). IB(4)(Di)=−βB(3)(Di)logαB(3)(Di).
定义 1.16 给定决策表 ( U , A , D ) , U / D = { D 1 , D 2 , ⋯ , D r } (U, A, D), U / D=\left\{D_{1}, D_{2}, \cdots, D_{r}\right\} (U,A,D),U/D={D1,D2,⋯,Dr}, 决策表的相对决策自信息定义如下:
I B ( 4 ) ( D ) = ∑ i = 1 r I B ( 4 ) ( D i ) . I_{B}^{(4)}(D)=\sum_{i=1}^{r} I_{B}^{(4)}\left(D_{i}\right). IB(4)(D)=i=1∑rIB(4)(Di).
定义 1.17 给定决策表 ( U , A , D ) , B ⊆ A (U, A, D), B \subseteq A (U,A,D),B⊆A,称 B B B 是相对于决策 D , A D , A D,A 的一个约简,若 B B B 满足以下条件:
(1) I B ( 4 ) ( D ) = I A ( 4 ) ( D ) I_{B}^{(4)}(D)=I_{A}^{(4)}(D) IB(4)(D)=IA(4)(D);
(2) I B − { a } ( 4 ) ≠ I B ( 4 ) I_{B-\{a\}}^{(4)} \neq I_{B}^{(4)} IB−{a}(4)=IB(4), 对于任意 a ∈ B a \in B a∈B.
2 应用举例
演示四种领域自信息的计算过程。直接贴图片吧,嘻嘻嘻…
表 4 − 1 4-1 4−1 中给出模糊 决策表 ( U , A , D ) (U, A, D) (U,A,D), 其中论域 U = { x 1 , x 2 , ⋯ , x 6 } U=\left\{x_{1}, x_{2}, \cdots, x_{6}\right\} U={x1,x2,⋯,x6}, A = { a 1 , a 2 , a 3 } A=\left\{a_{1}, a_{2}, a_{3}\right\} A={a1,a2,a3} 是条件属性集, D = { D 1 , D 2 } D=\left\{D_{1}, D_{2}\right\} D={D1,D2} 是模糊决策集。
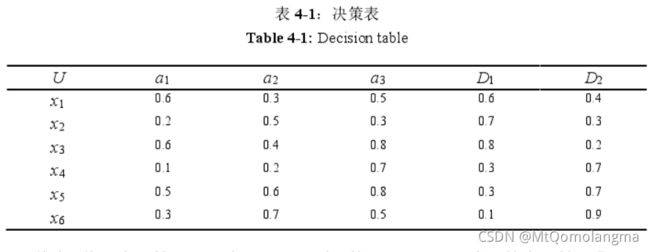
首先, 将三个属性归一化在区间 [ 0 , 1 ] [0,1] [0,1] 内。然后, 用以下公式计算在属性子集 B B B 下,样本 x i x_{i} xi 和, x j x_{j} xj 的模糊相似度 r i j ( i ≠ j ) r_{i j}(i \neq j) rij(i=j).
r i j = 1 − 1 m ∑ k = 1 m ( x i k − x j k ) ∧ 2 r_{i j}=1-\frac{1}{m} \sqrt{\sum_{k=1}^{m}\left(x_{i k}-x_{j k}\right)^{\wedge} 2} rij=1−m1k=1∑m(xik−xjk)∧2



计算每个模糊决策的下近似和上近似,结果如表4-2到表4-5所
示:



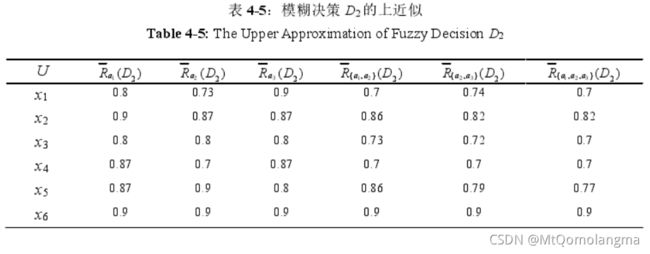
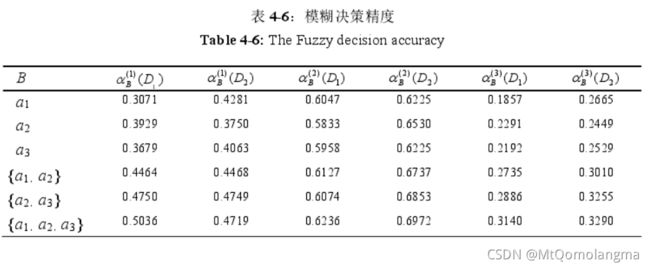
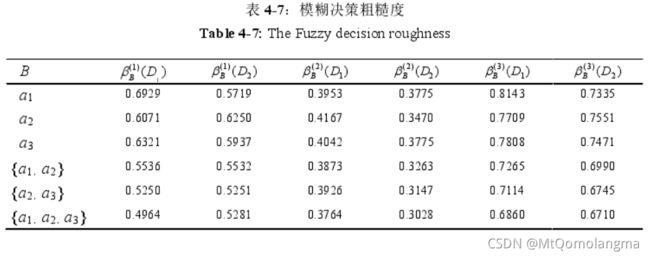
计算模糊决策 D 1 D_1 D1 和模糊决策 D 2 D_2 D2 的决策精度和粗糙度,结果列于表4-6和表4-7中。
计算四个模糊自信息值,结果列于表4-8中。

从表4-8中的信息可以看出以下四条结论:
(1)每种自信息值可以反映特征子集的分类能力。
(2)随着特征的增加,四种决策自信息的价值都会降低,决策的不确定性也逐渐变小。
(3)安全决策自信息仅考虑下近似提供的不确定性信息,而风险决策自信息仅考虑由上近似提供的不确定性信息。
(4)决策表的安全性和风险自信息可以表示由 I B ( 3 ) ( D ) I_{B}^{(3)}(D) IB(3)(D) 或 I B ( 4 ) ( D ) I_{B}^{(4)}(D) IB(4)(D) 表示。然而, 当特征数量增加时, I B ( 4 ) ( D ) I_{B}^{(4)}(D) IB(4)(D) 的减小率更快, 并且 I B ( 4 ) ( D ) I_{B}^{(4)}(D) IB(4)(D) 具有较强的收敛效应。
3 小结
心若有所向往,何惧道阻且长!共勉!
参考文献
[1]黄洋. 基于自信息测度的特征选择方法研究[D].渤海大学,2019.