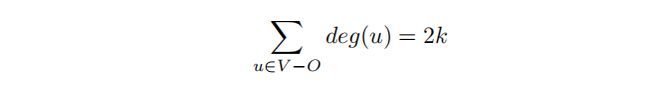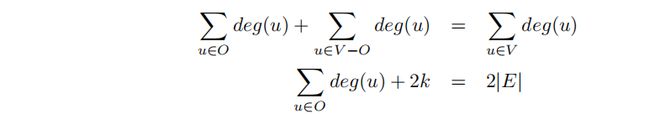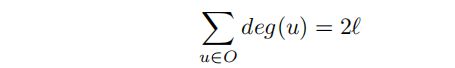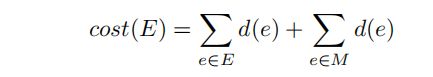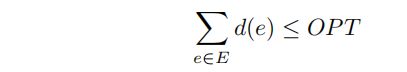【论文翻译】TSP-问题（4个变体）TRAVELLING-SALESMAN-PROBLEM (4 variants)

TSP-问题（4个变体）TRAVELLING-SALESMAN-PROBLEM (4 variants)

该文章仅作为学习记录。
需要原文pdf可私信

摘要

旅行推销员问题的目标是找到一个以最小的成本连接图中所有顶点的旅行。有几个变体，这取决于是否允许重复访问，也取决于距离是否满足一个度量。我们讨论了这些变量之间的关系，并给出了一个简单的2-近似算法。然后，我们开发了一个更复杂的1.5近似算法，将TSP与欧拉旅行联系起来。

1. 旅行推销的问题

今天，我们考虑旅行推销员-问题，通常缩写为TSP。“TSP”可能是最著名的（也是研究最多的）组合优化问题（COP）之一

1.1问题定义

给定一组城市（即点或顶点），TSP的目标是找到一个访问所有点的最小成本环形路线（或循环或巡回）。更正式地说，这个问题的表述如下：

Defifinition 1 ：

​ 给定一个n个点的集合V和一个距离函数$d：V\times V\to R$，找到一个包含V中所有点的最小代价的循环C。一个循环$C=（e1，e2，\dots \dots ，en）$的代价被定义为${\sum }_{e\in C}d(e)$，我们假设距离函数是非负的（即$d（x，y）\ge 0$）。

​ 请注意，不像斯坦纳树问题，这没有斯坦纳顶点：你必须访问每个城市。城市/点可能在某个几何空间中（例如，欧几里得平面），也可能不是。如果这些点在欧几里得平面上，那么就可以很自然地定义d为欧几里得距离。否则，d可以是任意的，即非度量的。关于TSP的一个实例的示例，请见图1。

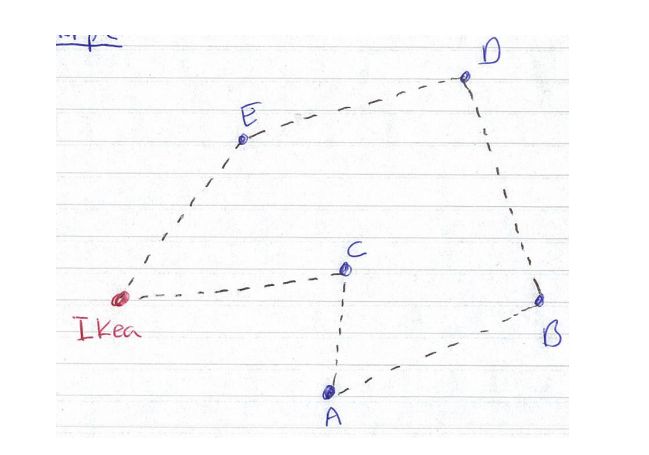
图1：TSP的示例。这里有六个地点。问题是找到最短的送货线路，从宜家开始参观五家房子，然后返回宜家。

1.2变体

与斯坦纳树问题一样，有几个变体：

​ •度量vs。一般情况：在TSP的度量版本中，距离函数d是一个度量版本，即它满足三角形不等式。在一般版本中，d可以给一条边分配任意的权值。

​ •重复访问vs。不重复：TSP的目标是找到一个访问每个顶点的循环。该循环是否可以包含重复的顶点（还是必须是一个简单的循环）？在没有重复的版本中，TSP环路必须精确地访问每个顶点一次。在重复的版本中，每个顶点的访问多于一次是可以接受的（如果这导致更短的路径）

我们将把这四种变体总结如下

1.3 NP-hard

TSP的所有变体都是np-hard。

对于这个问题的无重复变体，这很容易从哈密顿循环问题的简化中看出：哈密顿循环是一个只包含每个顶点一次的循环；哈密顿循环问题的目标是确定一个给定的图是否有一个哈密顿循环。决定一个图是否有一个哈密顿循环是np困难的（这可以通过从3-SAT开始的简化来证明）。显然，如果我们可以解决TSP，那么我们就可以解决哈密顿循环问题（通过正确地设置距离）。对于其他变体也有类似的减少。

TSP的一般无重复版本（G-NR-TSP）是np的，甚至很难近似！所以我们将在这个讲座中暂时忽略这个变体。

即便如此，我们还是要看看如何（很容易地做到！）近似于其他三个变体。在几乎所有常见的现实情况下（例如，距离函数满足三角形不等式，或者重复是可以接受的），有很好的近似算法。

2. 等效

我们要看到的第一件事是，其他三个变体是等价的。也就是说，M-R-TSP、M-NR-TSP和G-R-TSP都是等价的：如果我们为这些变体中的任何一个构造c-近似算法，那么我们也可以为其他两个变体构造一个c-近似算法。

我们首先关注重复的问题：只要距离函数是一个度量标准，那么我们是否允许重复并不重要。在很多方面，这应该并不令人惊讶（考虑到我们上周对斯坦纳-树的讨论）：如果我们在环路上有重复的顶点，我们总是可以以相同的成本“缩短”通过它们，产生一个不重复的循环

Lemma 2

当且仅当存在一个关于M-R-TSP（可度量可重复）的c近似算法时，才存在一个关于M-NR-TSP（可度量不可重复）的c近似算法。

Proof

这个证明有三个主张。首先，我们证明了带有重复和无重复的版本具有相同的最优代价。然后，我们展示了如何将解决方案从NR变体转换为R变体（这是琐碎的），并从R变体转换为NR变体（这包括跳过重复）。

Claim 1.

设（V，d）是Metric TSP的输入（对于NR或R变量）。设OPT ®为整体最小成本TSP环路（即有重复），并设OPT（NR）为无重复的最小成本TSP环路。然后是$OPT(R)=OPT（NR）$。

为了证明这一点，首先，我们观察到任何没有重复的循环也是一个合法的整体tsp环路（即，对于允许重复的版本）。因此，紧接着是，$OPT(R)\le OPT（NR）$— Part A.

接下来，让C是一个带有重复序列的循环，例如：

​ C = 0、1、2、3、2、4（，0）

我们现在可以通过跳过重复的顶点来创建循环C’。例如：

​ C ’ = 0、1、2、3、4（、0）

通过三角形不等式，我们知道$d（C^{\prime }）\le d(C)$.例如，在从C构造C’时，我们将（3,2,4）替换为（3,4）；我们知道$d（3,4）\le d（3,2）+d（2,4）$，用三角形不等式。我们可以对每个被跳过的顶点归纳地重复这个过程。

如果我们假设环路C=OPT ®，那么我们得出结论，$OPT（NR）=d(C^{\prime })\le d(C)=OPT(R)$— Part B.

把两个不平等在Part A.和Part B.，我们已经表明OPT（NR）≤OPT ®和OPT®≤OPT（NR），产生我们想要的结论，OPT ® =OPT（NR）

Claim 2.

如果A是M-NR-TSP的c近似算法，那么A也是M-R-TSP的c近似算法。

假设算法A输出环路C。假设C没有重复，$d(C)\le c\cdot OPT(NR)$。（$d（C）$为c近似算法计算出的解值，$OPT(NR)$为最优解的值）

因为Claim 1 $OPT(R)=OPT（NR）$，我们有==$d(C)\le c\cdot OPT(R)$==。因此，我们看到C也是M-R-TSP的一个有效的解决方案，并提供了一个C-近似。

Claim 3.

如果A是M-R-TSP的c-近似算法，那么我们可以构造一个算法A’，它是M-NR-TSP的c-近似算法。

具体来说，构造算法A’如下：运行算法A得到循环C（可能有重复）；然后通过跳过任何重复的顶点从C中构造C’。有两件事我们必须展示出来。

首先，环路C的代价是M-NR-OPT的一个很好的近似，即$d(C)\le c\cdot OPT(R)$。因为Claim 1中的$OPT(R)=OPT（NR）$，我们有 $d(C)\le c\cdot OPT（NR）$。

其次，我们在A’中构造的环路的代价以C的代价为界，即由于三角形不等式而导致的$d（C’）\le d(C)$，类似于Claim 1。

将这两个事实放在一起，我们可以看到产生C’的算法A’是M-NR-TSP的c近似算法，为$d（C^{\prime }）\le d(C)\le c\cdot OPT（NR）$。

​ 只要我们允许重复，我们就可以为一般版本和度量版本显示完全相同类型的等价性。在这种情况下，我们不能创建“捷径”，因为三角形不等式不成立；然而，我们不需要创建捷径方式，因为重复是允许的。

Lemma 3

当且仅当存在G-R-TSP的c近似算法时，才存在M-R-TSP的c近似算法。

Proof

​ 在这种情况下，证明包含两个主张：一个将G转化为M（这是平凡的），另一个将M转化为G（需要一些工作）。

Claim 1.

​ 如果A是G-R-TSP的c近似算法，那么A是M-R-TSP的c近似算法。这一说法立即显然是正确的。这两个问题是相同的，除了对M-R-TSP的输入必须是一个度量的限制。但是，如果一个给定的输入是一个度量，那么它显然满足G-R-TSP的要求，我们可以只在该实例上执行算法A。此外，G-R-TSP和M-R-TSP的最优解将是相同的（因为它们是在完全相同的可能循环集上进行优化的）。

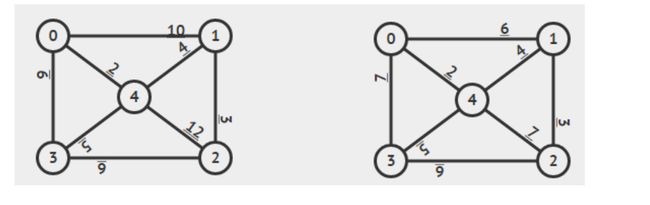
图2：构建A’的例子，将G-R-TSP简化为M-R-TSP，例如C = {0、4、1、2、3、0}，然后是C ’ = {0、4、1、2、3、4、0}。

Claim 2.

如果A是M-R-TSP的c-近似算法，那么我们可以构造算法A’是G-R-TSP的c-近似算法。

​ 设$（V，d_g）$为算法A’的输入，即G-R-TSP的输入。我们构造算法A’如下。

​ 首先，我们需要构造一个距离度量$d_m$。对于每一对顶点（u、v），根据距离$d_g$，将$d_m（u、v）$定义为从u到v的最短路径。（回想一下，$d_g$不是一个度量量，也就是说，不一定满足三角形不等式。）我们可以通过在V上构造完整的图，将边（u，v）的权值赋值为$d_g（u，v）$，并执行一个全对最短路径算法，例如$O（V^3）$FloydWarshall的算法来找到$d_m$。你会注意到$d_m$现在是一个距离度量，也就是说，它满足三角形不等式。回想一下，dm被称为图的度量补全。

​ 第二，执行算法$A$ on$（V、d_m）$，生成环路C。然后我们需要用C来构造一个新的循环C’ 。对于每条边（u，v），我们根据$d_g$将从u到v的最短路径添加到我们的输出环路C’中。注意，这将产生一个可能包含可能重复的顶点的循环C’。

​ 我们现在认为这个结果是$OPT（V，d_g）$的一个很好的近似值。首先，观察$d（C^{\prime }）=d(C)$。C中的每条边都被C’中的一条路径所取代，其成本完全相同，因此我们最终得到了相同的成本环路。其次，我们知道假设$d(C)\le c\cdot OPT（V，d_m）$，通过假设A是一个c-近似算法。

​ 最后，我们提出了$OPT（V，d_m）\le OPT（V，d_g）$。特别地，如果R是$（V，d_g）$的最优环路，那么R也是$（V，d_m）$中的一个环路。此外，对于每一对（u，v），我们知道$d_m（u，v）\le d_g（u，v）$（因为$d_m$被定义为最短路径）。因此，$d_m(R)\le d_g(R)$。由于具有度量$d_m$的最优循环必须至少与$d_m(R)$一样好，我们得出结论，$OPT（V，d_m）=d_m(R)\le d_g(R)=OPT（V，d_g）$。

​ 综合这些部分，我们得出$d（C^{\prime }）=c\cdot OPT（V，d_m）\le c\cdot OPT（V，d_g）$，因此算法A’是G-R-TSP的c-近似算法。

3. 2近似算法

​ 我们现在提出了一种G-R-TSP的2-近似算法。我们已经知道，这也将产生一个针对其他两个变体的2-近似算法。假设输入是（V，d），其中V是一组点，d是一个距离函数（但不一定是一个度量）。请考虑以下算法：

1.构造权值为w的完整图G =（V，E），其中E包含每对（u，v）∈V×V和w（u，v）= d（u，v）。

2.设T为G的最小生成树

3.设C是通过对T进行深度优先搜索而构造的环路。

​ 为了分析这个算法，像往常一样，我们从最优解开始，然后向后工作。设$C^{\ast }$为输入（V，d）的最优（最小成本）TSP环路，设$E^{\ast }$为$C^{\ast }$中的边。请注意，图$G^{\ast }=（V，E^{\ast }）$是联通的，因为$C^{\ast }$是一个包含每个点的循环。设$T^{\ast }$为$G=（V，E^{\ast }）$的最小生成树。在这一点上，我们知道：
$d(T^{\ast })\le d(C^{\ast })=OPT$

由于树T是G =（V，E）和$E^{\ast }\subseteq E$的最小生成树，所以我们知道：

​ $d(T)\le d(T^{\ast })$

最后，由于C是由T的深度优先搜索遍历构造的，我们知道C将T中的每条边恰好包含了两次，因此：

​ $d(C)=2\times d(T)$

把这些不等式综合在一起，我们得出结论：

​ $d(C)=2\times d(T)\le 2\times d(T^{\ast })\le 2\times d(C^{\ast })\le 2\times OPT$

也就是说，C的代价最多是OPT的代价的两倍，因此该算法是一个2-近似的算法

4. 欧拉回路

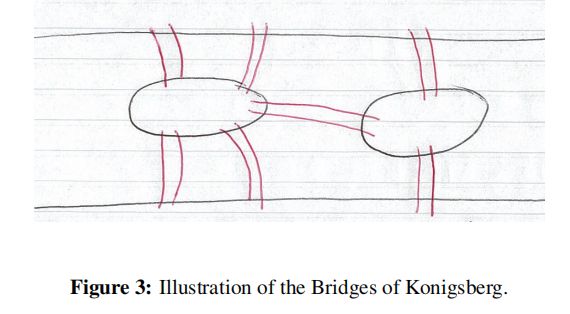
​ 我们现在想开发一个更好的近似算法，它将比2有更好的近似比。为了做到这一点，我们将需要一些额外的工具。让我们从一个著名的问题开始，被称为哥尼斯堡的桥

​ 在哥尼斯堡，有一条有两个岛屿的河流。在历史上，这两个岛屿是由七座桥连接起来的。这些桥既漂亮又有名，所以每个人都想回答的问题是，是否有可能恰好穿过每座桥一次，最后回到你开始的地方。稍微一思考，很明显你做不到。但你能怎么证明呢？欧拉解决了这个问题，他的解决方案通常被认为标志着图论作为一个数学领域的开始。值得注意的是，他意识到这个问题可以用一个图表来表示：

​ 一旦这个问题被抽象地表示为一个图，我们就可以应用更强大的技术来解决这个问题。在本节中，我们将讨论多重图，而不是简单的图。一个多图是一个图G =（V，E），其中E是一个边的multiset，而不是一个set。这意味着每条边都可以在图中出现不止一次。例如，一条给定的边（u，v）可能会在图G中出现四次。

Defifinition 4

一个多图G中的欧拉回路是一个恰好跨越每一条边一次的循环。

​ 请注意，与tsp循环不同，欧拉回路关注的是边，而不是顶点。我们的目标是恰好跨越每条边一次——尽管这可能意味着要多次访问一个给定的顶点。显然，哥尼斯堡桥的问题只是在问，在相关的图中是否存在一个欧拉循环。

关键的要求是检测一个图何时具有欧拉回路。令人惊讶的是，有一个非常简单的描述：

Lemma 5

多图G =（V，E）具有欧拉回路当且仅当：

•它是相互联通的（具有0度的顶点除外）。

•每个顶点都有偶数度。

证明过程就略了，想看的可以下载pdf

5. 有一个更好的TSP近似值

我们再次考虑M-R-TSP变体，就像之前一样，如果我们可以为这个变体有一个c-近似算法，那么我们也可以近似其他两个变体： M-NR-TSP和G-R-TSP。假设（V，d）是我们的问题的输入。

5.1基本思想

​ 假设我们构建了一个包含欧拉循环的多图G =（V，E）。然后这个循环将给TSP问题提供一个可行的解决方案。相反地，如果对TSP问题有一个解决方案，我们就可以构建一个只由TSP循环中的边组成的多重图，这将得到一个具有欧拉循环的图。因此，求解TSP等价于找到E边的最小代价集，使G =（V，E）有一个欧拉循环。

1.求出权值由d定义的V上的完备图的最小生成树 T。

2.将T中的每条边两次添加到集合e中。这确保了V中的每个顶点具有偶数度。

3.由于多重图G =（V，E）中的每个顶点都有偶数度，因此我们可以找到G的欧拉循环C。

4.返回C（跳过重复的顶点）。

​ 这是解决TSP问题的正确算法。不幸的是，它不会比之前的2-近似算法产生任何改进，因为我们仍然在MST中添加每条边两次，导致代价最少是两倍最优的。

​ 请注意，将每条边添加两次是非常低效的！我们唯一的目标是确保每个顶点都有偶数度——如果一个顶点已经有偶数度，为什么我们要把它的所有输出边加倍，从而增加我们的成本？请考虑图5中的示例。

​ 图5：通过创建具有偶数度的顶点来寻找TSP的示例。最初，我们有一个有九条边的图。如果我们把每条边加倍，我们就有一个有18条边的图。但是，如果我们想确保每个顶点具有偶数度，那么只向图添加一条边就足够了，从而得到一个只有10条边的图。

​ 因此，我们必须回答的问题是：我们如何将最小的边数加到一个多重图中，以确保每个顶点具有偶数度？因此，总之，所得到的算法应该如下所示：

1.求出权值由d定义的V上的完备图的MST T

2.将T中的每条边都加到集合E中。

3.将边E’的最小代价集加到E中，这样在E∪E’中，每个顶点都是偶数度。

4.由于多图G =（V，E∪E’）中的每个顶点都有偶数度，因此我们可以找到G的欧拉循环C

5.返回C（跳过重复的顶点）。

​ 我们已经知道成本(T)≤成本（OP T），因为最优的tsp循环也是一个生成树（一旦你删除了一条边）。关键是要证明cost（E’）≤OP T /2。

5.2 匹配

我们需要的最后一个工具是一个完美的匹配：

Defifinition 6

我们说，如果M中没有两条边共享一个端点，（V，M）是匹配的，即V中的所有顶点都是度≤1。如果V中的每个顶点都是度为1，即每个顶点都是匹配的，我们说（V，M）是完全匹配的。

请注意，一个完美的匹配只有在|V |为偶数时才存在：如果有奇数个顶点，显然不可能全部匹配它们。

如果每条边都有一个权值，那么我们可能想要找到最小代价的完美匹配。组合优化的最优的结果之一恰恰是：

Theorem 7

有一个多项式时间算法来寻找最小代价完美匹配。

​ 这就找到了最优的解决方案，而且它很有效！不幸的是，这个算法超出了今天的类的范围。(参见埃德蒙兹的算法[1]。这个解决方案包括他著名的寻找匹配的开花算法，以及原对偶方法和线性规划。)现在，我们只是假设我们可以找到一个最小成本的完美匹配。

5.3 Evens and Odds

我们想使用完美匹配的思想来配对具有奇度的多重图中的顶点。如果我们能给他们每个人分配一个伴侣，那么他们就会有偶度。但是有一个潜在的问题：如果有一个奇数个的顶点需要一个pattern怎么办？幸运的是，这是不可能的，因为有一个很好的计数论点：

Lemma 8

在每个图G =（V，E）中，都有一个偶数个具有奇数度的顶点。

Proof

设O为奇度顶点的集合，V−O为偶次顶点的集合。设deg (u)为u的度。

Recall that we can count the number of edges in the graph by summing up the total degree and diving by 2, i.e.

也就是说，所有顶点的度之和是偶数的。现在，只考虑V−O中的顶点：因为每个顶点都是偶数，它们的度之和也必须是偶数：

总结一切，我们得出结论：

由于表达式的右侧为偶数，所以表达式的左侧也必须为偶数。即：

但是O中的每个顶点都有奇数度。因此它们的度之和是偶数的唯一方法是如果有一个奇数顶点，即|O|是偶数。

5.4 Christofifides Algorithm

把这些碎片放在一起，我们现在有了以下算法：

1.求出权值由d定义的V上的完备图的MST T。

2.将T中的每条边都加到集合E中

3.设O是T中具有奇度的顶点。请注意，|O|是偶数的。

4.设M是O的最小成本完美匹配。

5.构造多重图G =（V，E∪M）。

6.由于多图G =（V，E∪M）中的每个顶点都有偶数度，因此我们可以找到G的欧拉循环E。

7.返回E（跳过重复的顶点）

为了分析这一点，我们注意到成本包括以下内容：

该表达式的第一部分来自于MST，因此我们已经知道：

​ 由于OPT形成了一个循环，我们可以从循环中移除任何边，得到一个生成树；MST T的成本必须不大于这个循环。

​ 我们现在需要论证$2\times {\sum }_{e\in M}d(e)\le OPT$。设C是OP T的循环。设C’和C是相同的循环，我们跳过V−O中的所有顶点，然后跳过重复。也就是说，C’是一个没有重复的奇数顶点上的循环。注意cost（C '）≤cost©，因为我们只跳过顶点（三角形不等式成立）。

另外，请注意，循环$C^{\prime }$有偶数个顶点（因为有偶数个奇数顶点）和偶数个边。假设$C^{\prime }=（v_1，v_2，\dots \dots ，v_{2k}）$。

我们现在可以构造两个不同的完美匹配M1和M2。我们对它们的定义如下：

$M_1 = (v_1, v_2),(v_3, v_4),(v_5, v_6), . . . ,(v_{2k−1}, v_{2k}) $

$M_2=(v_2,v_3),(v_4,v_5),(v_6,v_7),...,(v_{2k},v_1)$

注意，每个完美匹配都有k = |O|/2边，并且两者都是集合O的有效完美匹配。由于M是最小代价完美匹配，我们得出结论：

$cost(M)\le cost（M_1）$

$cost(M)\le cost（M_2）$

但是，请注意，$cost（M_1）+cost（M_2）=cost（C^{\prime }）\le cost(C).$所以，如果我们把匹配结果相加，我们就会得到：

$2\times cost(M)\le cost（M_1）+cost（M_2）\le cost(C)=OPT$

因此，我们已经证明了$cost(M)\le OPT/2$。

把这些部分放起来，我们可以看到算法输出环路的代价是：

因此，我们发现了M-R-TSP的1.5近似算法。