【python和机器学习入门2】决策树2——决策树构建
参考博客:决策树实战篇之为自己配个隐形眼镜 (po主Jack-Cui,《——大部分内容转载自
参考书籍:《机器学习实战》——第三章
目录
一 构建决策树
1.1 决策树构建原理
1.2 决策树结构
1.3决策树构建关键代码
1.4 构建完整代码
1.5 使用构建的决策树进行预测分类
二 决策树的存储
《——决策树概念子模块等见前篇
一 构建决策树
依旧是用贷款demo,数据如下
本章使用ID3算法进行决策树划分,每次划分消耗一个特征属性。
1.1 决策树构建原理
决策树构建工作原理:从原始数据集开始,基于最好的属性值划分数据集,由于特征值可能多于两个,因此可能存在大于两个分支的数据集划分。第一次划分之后,数据集被向下传递到树的分支的下一个结点。在这个结点上,我们可以再次划分数据。因此我们可以采用递归的原则处理数据集。
使用ID3算法的核心是在决策树各个结点上对应信息增益准则选择特征,递归地构建决策树。具体方法是:从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子节点;再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止,最后得到一个决策树。ID3相当于用极大似然法进行概率模型的选择。
递归创建决策树时,递归有两个终止条件:第一个停止条件是所有的类标签完全相同,则直接返回该类标签;第二个停止条件是使用完了所有特征,仍然不能将数据划分仅包含唯一类别的分组,即决策树构建失败,特征不够用。此时说明数据纬度不够,由于第二个停止条件无法简单地返回唯一的类标签,通常采用多数表决即挑选出现数量最多的类别作为返回值。
根据该构建原理对贷款demo进行数据集划分,从上篇我们知道根的信息增益最大是“是否有房”特征属性,根据这个属性可以划分2个数据集D1、D2如下,且D1数据集中的贷款类别全为“是”,即全为同一类,该数据集结点即可停止划分。
1.2 决策树结构
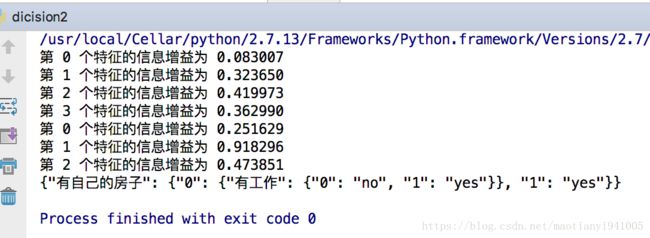
贷款demo的信息增益计算过程如下,前4行为第一次划分数据集,信息增益最高为第3个,取为根节点,删除该特征后再次计算,得到第2个特征信息增益最高,取为第二个划分特征。
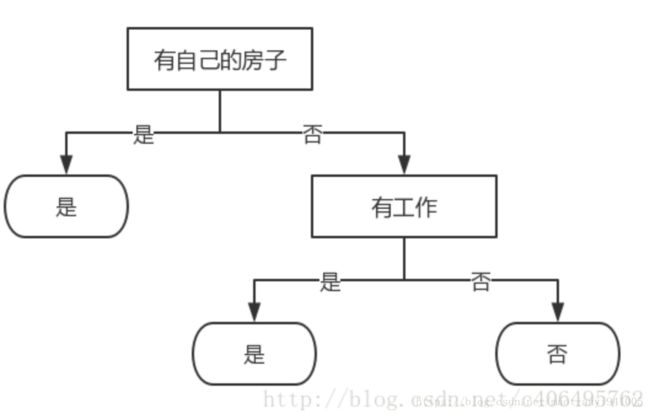
可以知道第一个划分特征为“有自己的房子”,第二个划分特征为“有工作” ,且划分之后子集正好都是同一类,即终止节点。故决策树构建完成如下:
使用字典存储决策树结构,如
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}字典关键字(key)‘有自己的房子’是第一个划分数据集的特征名称,它的值(value)是另一个字典。value要么是类标签,要么是另一个字典。如果值是类标签则该子节点是叶子节点;如果值是另一个字典,则子节点是一个判读节点,这种格式不断重复构成了整棵树。
1.3决策树构建关键代码
(这部分代码解析来自po主Jack-Cui,写的很详细 我就扣过来了)
函数createTree(dataset,labels)返回创建的字典决策树,
各子模块代码详细解释见前篇
伪代码(递归建树函数createTree):
判断是否为两类终止类型,如果是则返回分类(majorityCnt
若不是则向下建树:
找最优特征(chooseBestFeatureToSpit()《——splitdataset、calShannonEnt)、
ID3消耗特征(del()
获取该特征的属性值并循环划分子集(splitdataset)、
子集递归建树 (createTree
list.count() 方法用于统计某个元素在列表中出现的次数。
del() 删除元素。注意del 是删除引用而不是删除对象,对象由自动垃圾回收机制(GC)删除
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] #取分类标签(是否放贷:yes or no)
if classList.count(classList[0]) == len(classList): #如果类别完全相同则停止继续划分
return classList[0]
if len(dataSet[0]) == 1: #遍历完所有特征时返回出现次数最多的类标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel = labels[bestFeat] #最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #根据最优特征的标签生成树
del(labels[bestFeat]) #删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] #得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) #去掉重复的属性值
for value in uniqueVals: #遍历特征,创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels, featLabels)
return myTree
1.4 构建完整代码
#!/usr/bin/env python
#_*_coding:utf-8_*_
import numpy as np
import json
import operator
from math import log
''''''
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], #数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况'] #特征属性
return dataSet, labels #返回数据集和特征属性
'''经验熵'''
def calShannonEnt(dataset):
m = len(dataset)
lableCount = {}
'''计数'''
for data in dataset:
currentLabel = data[-1]
if currentLabel not in lableCount.keys():
lableCount[currentLabel] = 0
lableCount[currentLabel] += 1
'''遍历字典求和'''
entropy = 0
for label in lableCount:
p = float(lableCount[label]) / m
entropy -= p * log(p,2)
return entropy
'''第i个特征根据取值value划分子数据集'''
def splitdataset(dataset,axis,value):
subSet = []
for data in dataset:
if(data[axis] == value):
data_x = data[:axis]
data_x.extend(data[axis+1:])
subSet.append(data_x)
return subSet
'''遍历数据集求最优IG和特征'''
def chooseBestFeatureToSpit(dataSet):
feature_num = len(dataSet[0])-1
origin_ent = calShannonEnt(dataSet)
infoGain = 0.0
best_infogain = 0.0
for i in range(feature_num):
fi_all = [data[i] for data in dataSet]
fi_all = set(fi_all)
#print fi_all
subset_Ent = 0
'''遍历所有可能value'''
for value in fi_all:
#划分子集
#print i,value
subset = splitdataset(dataSet,i,value)
#print subset
#计算子集熵
p = float(len(subset)) / len(dataSet)
subset_Ent += p * calShannonEnt(subset)
#计算信息增益
infoGain = origin_ent - subset_Ent
#记录最大IG
print "第 %d 个特征的信息增益为 %f" % (i,infoGain)
if(infoGain > best_infogain):
best_feature = i
best_infogain = infoGain
return best_feature
'''计数并返回最多类别'''
def majorityCnt(classList):
classCount = {}
for class_ in classList:
if(class_ not in classCount.keys()):
classCount[class_] = 0
classCount[class_] += 1
classSort = sorted(classCount.iteritems(),key = operator.itemgetter(1),reverse=True)
return classSort[0][0]
'''向下递归创建树 '''
def createTree(dataSet,labels,feaLabels):
'''数据集所有类别'''
classList = [example[-1] for example in dataSet]
'''判断是否属于2个终止类型'''
'''1 全属一个类'''
if(len(classList) == classList.count(classList[0])):
return classList[0]
'''2 只剩1个特征属性'''
if(len(dataSet[0]) == 1):
majorClass = majorityCnt(classList)
return majorClass
'''继续划分'''
best_feature = chooseBestFeatureToSpit(dataSet)#最优划分特征 下标号
best_feaLabel = labels[best_feature]
feaLabels.append(best_feaLabel) #存储最优特征
del(labels[best_feature])#特征属性中删去最优特征《——ID3消耗特征
feaValue = [example[best_feature] for example in dataSet]
feaValue = set(feaValue) #获取最优特征的属性值列表
deci_tree = {best_feaLabel:{}}#子树的根的key是此次划分的最优特征名,value是再往下递归划分的子树
for value in feaValue:
subLabel = labels[:]
subset = splitdataset(dataSet,best_feature,value)
deci_tree[best_feaLabel][value] = createTree(subset,subLabel,feaLabels)
return deci_tree
if __name__ == '__main__':
dataSet, labels = createDataSet()
feaLabels = []
print json.dumps(mytree,ensure_ascii=False)
决策树构建结果
1.5 使用构建的决策树进行预测分类
决策树构建完毕后,接下来使用进行实际数据的分类。在执行数据分类的时候,程序比较测试数据和决策树上的值,比如决策树根为“有自己的房子”,读取测试数据该标签上的值,根据值进入到下一节点,递归执行该过程直到进入叶子节点,最后将测试数据预测的分类定义为最终走到的叶子节点所属的类型。
type() 只有一个参数时返回对象的类型 属性值__name__获取类型名
list.index()返回元素索引
'''预测分类'''
'''feaLabels,testdata特征对应顺序应一样'''
def classify(inputTree,feaLabels,testdata):
firstStr = inputTree.keys()[0]
#print firstStr
secondDict = inputTree[firstStr]
#print secondDict
'''获取测试数据在此特征上的值'''
testvalue = testdata[feaLabels.index(firstStr)]
for value in secondDict.keys():
if(value == testvalue):
if(type(secondDict[value]).__name__ == 'dict'):
classLabel = classify(secondDict[value],feaLabels,testdata)
else:
classLabel = secondDict[value]
return classLabel
if __name__ == '__main__':
dataSet, labels = createDataSet()
feaLabels = []
mytree = createTree(dataSet,labels,feaLabels)
print feaLabels
print json.dumps(mytree,ensure_ascii=False)
testdata = [0,1]
classresult = classify(mytree,feaLabels,testdata)
if(classresult == 'yes'):
print "准许贷款"
else: print "拒绝贷款"
二 决策树的存储
构造决策树是很耗时的任务,即使处理很小的数据集,如前面的样本数据,也要花费几秒的时间,如果数据集很大,将会耗费很多计算时间。然而用创建好的决策树解决分类问题,则可以很快完成。因此,为了节省计算时间,最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题,需要使用Python模块pickle序列化对象。序列化对象可以在磁盘上保存对象,并在需要的时候读取出来。
'''存储决策树'''
def storeTree(inputTree,filename):
import pickle
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
'''读取决策树'''
def grabTree(filename):
import pickle
fr = open(filename)
return pickle.load(fr)三 总结
决策树的一些优点:
- 易于理解和解释,决策树可以可视化。
- 几乎不需要数据预处理。其他方法经常需要数据标准化,创建虚拟变量和删除缺失值。决策树还不支持缺失值。
- 使用树的花费(例如预测数据)是训练数据点(data points)数量的对数。
- 可以同时处理数值变量和分类变量。其他方法大都适用于分析一种变量的集合。
- 可以处理多值输出变量问题。
- 使用白盒模型。如果一个情况被观察到,使用逻辑判断容易表示这种规则。相反,如果是黑盒模型(例如人工神经网络),结果会非常难解释。
- 即使对真实模型来说,假设无效的情况下,也可以较好的适用。
决策树的一些缺点:
- 决策树学习可能创建一个过于复杂的树,并不能很好的预测数据。也就是过拟合。修剪机制(现在不支持),设置一个叶子节点需要的最小样本数量,或者数的最大深度,可以避免过拟合。
- 决策树可能是不稳定的,因为即使非常小的变异,可能会产生一颗完全不同的树。这个问题通过decision trees with an ensemble来缓解。
- 学习一颗最优的决策树是一个NP-完全问题under several aspects of optimality and even for simple concepts。因此,传统决策树算法基于启发式算法,例如贪婪算法,即每个节点创建最优决策。这些算法不能产生一个全家最优的决策树。对样本和特征随机抽样可以降低整体效果偏差。
- 概念难以学习,因为决策树没有很好的解释他们,例如,XOR, parity or multiplexer problems.
- 如果某些分类占优势,决策树将会创建一棵有偏差的树。因此,建议在训练之前,先抽样使样本均衡。