代码随想录刷题记录day19 二叉搜索树的最小绝对差+ 二叉搜索树中的众数(代码技巧)+二叉树的最近公共祖先
代码随想录刷题记录day19
[代码随想录](https://programmercarl.com/)
530. 二叉搜索树的最小绝对差
思想
双指针法,维护一个最小值,和一个pre指针,当前节点的前一个节点,做差值比较,要注意pre为null的情况
代码
class Solution {
public int min=Integer.MAX_VALUE;
public TreeNode pre=null;
public int getMinimumDifference(TreeNode root) {
minDiff(root);
return min;
}
public void minDiff(TreeNode node){
//递归终止条件
if(node==null) return ;
//中序遍历
// 左
if(node.left!=null) minDiff(node.left);
// 中
if(pre!=null && node.val-pre.val<min){
//递归第一个节点的时候 pre为空,就不会进入这个判断
min=node.val-pre.val;
}
pre=node;
if(node.right!=null) minDiff(node.right);
}
}
501. 二叉搜索树中的众数
思想
要求二叉树中出现最多的数字,最直观的想法就是遍历一颗二叉树,然后记录所有节点出现的次数,最后按照次数进行排序,得到结果。
排序使用java stream相关的API
-
将List 转换成一个int类型的数组
List<Integer> list =new ArrayList<>(); list.stream().mapToInt(Integer::intValue).toArray(); -
对map进行排序
先将map转换成List 再排序
List\<map.Entry\<Integer,Integer>> mapList=map.entrySet().stream() .sorted((c1,c2)-> c2.getValue().compareTo(c1.getValue())) .collect(Collectors.toList());
但是这是一颗二叉搜索数,利用二叉搜索树的特性,中序遍历可以按顺序输出。
如果是再有序数组上求最大频率,可以先遍历一遍数组,找出最大频率(maxCount),然后再重新遍历一遍数组,把出现频率为maxCount的元素放进集合。
利用代码的技巧可以一次遍历实现上述需求。
维护一个当前数出先的频率,count。
如果count==maxCount,就把当前的值放入结果集合。
如果count>maxCount 清空集合,maxCount=count,再把当前的元素放入集合。
在数组中可以这样实现
int[] array={1,2,2,4,4,7,7,7,9};
//目标 求出array中重复次数最多的元素
int count=0;
int maxCount=0;
List<Integer> list=new ArrayList<>();
int pre=0;
for (int i=0;i<array.length;i++){
if(pre==0){
//表示第一个节点
count=1;
}else if(pre!=0 && array[i]==pre){
count++;
}else{
count=1;
}
pre=array[i];
if(count==maxCount){
list.add(array[i]);
}else if(count>maxCount){
list.clear();
maxCount=count;
list.add(array[i]);
}
}
System.out.println(list);
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int count;
public int maxValue;
public List<Integer> list=new ArrayList<>();
public TreeNode pre=null;
public int[] findMode(TreeNode root) {
//一遍遍历的思路 真实妙哉
traversal(root);
int [] arrayRes=new int[list.size()];
for(int i=0;i<list.size();i++){
arrayRes[i]=list.get(i);
}
return arrayRes;
}
public void traversal(TreeNode node){
if(node==null) return ;
if(node.left!=null) traversal(node.left);
//真正的处理逻辑
if(pre==null){
//第一个节点为空
count=1;
}else if(pre!=null && node.val==pre.val){
//节点的值相同
count++;
}else{
//节点的值又不同了 count重置为1
count=1;
}
pre=node;
//到这里获取到了 当前节点的count值 但是还没有对maxValue 最大频率 进行操作
if(count==maxValue){
//最大频率 等于当前这个数 截至当前节点 出现的次数
list.add(node.val);
}
if(count>maxValue){
list.clear();
maxValue=count;
list.add(node.val);
}
//右
if(node.right!=null) traversal(node.right);
}
}
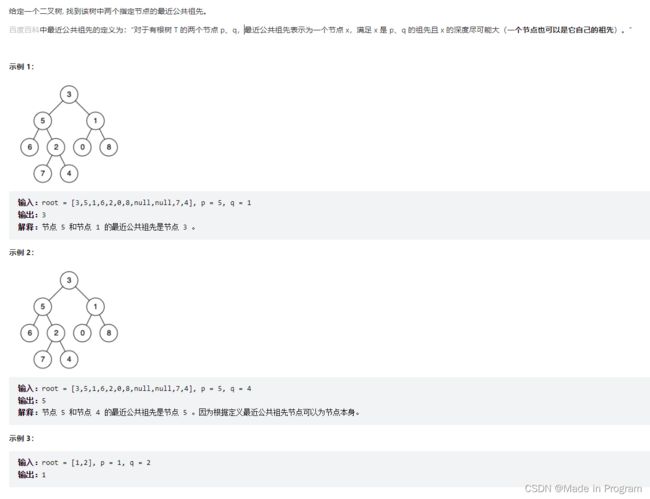
236. 二叉树的最近公共祖先
思想
回溯,采用后序遍历。
递归终止条件:当前节点为空 或者 当前节点找到了p 或者q 就返回当前节点
左:向左递归,返回值left表示左子树如何含有p或者q 会返回p或者q
右: 同上
中的逻辑:
左子树为空,右子树找到了一个节点,返回右子树的节点
右子树为空,左子树找到了一个节点,返回左子树的节点
都为空 返回null
代码
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//自底向上 用后序遍历 分别判断节点的左右子树 是否包含有p或者q
//递归终止条件
if(root==null) return root;
if(root==p || root ==q) return root;//找到了 p或者q 就不再想下遍历了
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left!=null && right!=null) return root;
//单层递归的逻辑
if(left==null && right!=null) return right;
else if(left!=null && right==null) return left;
else{
//都为空的情况
return null;
}
}
}