Python画常见分布的概率密度图

因为做概随大作业，了解了一些python画概率分布图的方法。

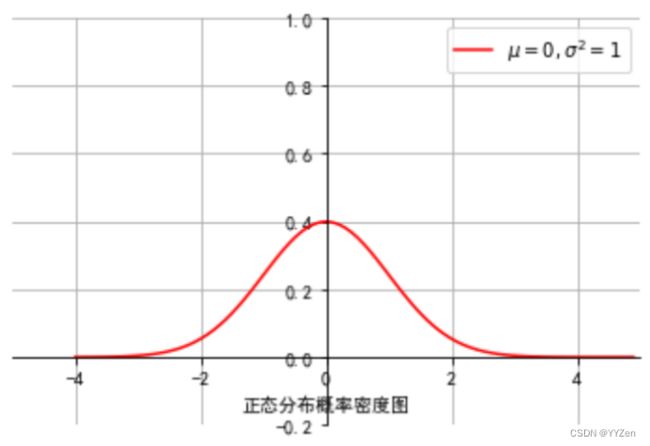
正态分布

代码如下：

import numpy as np
import math
import matplotlib.pyplot as plt
#设置中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def gd(x, mu=0, sigma=1):
    """根据公式，由自变量x计算因变量的值
    Argument:
        x: array
            输入数据（自变量）
        mu: float
            均值
        sigma: float
            方差
    """
    left = 1 / (np.sqrt(2 * math.pi) * np.sqrt(sigma))
    right = np.exp(-(x - mu)**2 / (2 * sigma))
return left * right

if __name__ == '__main__':
    #  自变量
    x = np.arange(-4, 5, 0.1)
    #  因变量（设置不同均值或方差）
    y = gd(x, 0, 1)
    #  绘图
    plt.plot(x, y, color='red')
    #  设置坐标系
    plt.xlim(-5.0, 5.0)
plt.ylim(-0.2, 1)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))
    # 网格线
plt.grid(True)
#标注
    plt.legend(labels=['$\mu = 0, \sigma^2=1$'])
    # 标题
plt.xlabel("正态分布概率密度图")
#展示
plt.show()

卡方分布

代码如下：

from scipy import stats
import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt
x = np.linspace(0,100,100000)
color = ["blue","brown","darkgrey","darkblue","red"]
for i in range(10,51,10):
    y=stats.chi2.pdf(x,df=i)
    plt.plot(x,y,c=color[int((i-10)/10)])
plt.title('卡方分布的概率密度函数')
plt.tight_layout()
plt.savefig(" 卡方分布的概率密度函数",dpi=300)

t分布

代码如下：

from scipy import stats
import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt
x = np.linspace(-5,5,100000)
y = stats.t.pdf(x,2)
plt.plot(x,y,c="orange")
plt.title('t分布的概率密度函数')

plt.tight_layout()
plt.savefig("t分布的概率密度函数",dpi=300)

F分布

代码如下：

from scipy import stats
import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt
x = np.linspace(-1,8,100000)
y1 = stats.f.pdf(x,1,10)
y2 = stats.f.pdf(x,5,10)
y3 = stats.f.pdf(x,10,10)
plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
plt.ylim(0,1)
plt.title('F分布的概率密度函数')
plt.tight_layout()
plt.savefig("F分布的概率密度函数",dpi=300)

运行结果：