数模培训第五周——数据处理方法

灰色系统模型及预测

灰色系统模型在数据处理和预测中经常使用。
灰色系统理论建模特点：原始数据必须等时间间距。
处理思路：首先对原始数据进行累加，弱化原始时间序列数据的随
机因素.然后建立生成数的微分方程。
GM(1,1)模型是灰色系统理论中的单序列一阶灰色微分方程。

介绍

设已知序列为$x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(n\right)$
做一次累加AGO (Acumulated Generating Operation）生成新序列:$x^{\left(1\right)}\left(1\right),x^{\left(1\right)}\left(2\right),\cdots ,x^{\left(1\right)}\left(n\right)$

其中：
$$x^{\left(1\right)}\left(1\right)=x^{\left(0\right)}\left(1\right),x^{\left(1\right)}\left(2\right)=x^{\left(1\right)}\left(1\right)+x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(1\right)}\left(n\right)=x^{\left(1\right)}\left(n-1\right)+x^{\left(0\right)}\left(n\right)$$

也即：
$$x^{\left(1\right)}\left(k\right)=\sum _{i=1}^k{x}^{\left(0\right)}\left(i\right)k=1,2,\cdots ,n$$

生成均值序列：

$$z^{(1)}(k)=\alpha x^{(1)}(k)+(1-\alpha )x^{(1)}(k-1)k=2,3,\dots ,n$$

其中$0⩽\alpha ⩽1$。通常可取$\alpha =0.5$
建立灰微分方程：
$$x^{(0)}(k)+a{z}^{(1)}(k)=bk=2,3,\dots ,n$$

相应的$GM(1,1)$白化微分方程为：

$$\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}(t)=b$$

将方程变形为
$$-a{z}^{(1)}(k)+b=x^{(0)}(k)k=2,3,\dots ,n$$

其中，$a,b$为待定模型参数。

将方程组采用矩阵表示为：

$$\left[\begin{array}{cc}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ \dots & \dots \\ -z^{(1)}(n)& 1\end{array}\right]\left(\begin{array}{l}a\\ b\end{array}\right)=\left(\begin{array}{c}{x}^{(0)}(2)\\ x^{(0)}(3)\\ \dots \\ x^{(0)}(n)\end{array}\right)$$

即：$X\beta =Y$

其中：

$$X=\left[\begin{array}{cc}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ \dots & \dots \\ -z^{(1)}(n)& 1\end{array}\right],\beta =\left(\begin{array}{l}a\\ b\end{array}\right),Y=\left(\begin{array}{c}{x}^{(0)}(2)\\ x^{(0)}(3)\\ \dots \\ x^{(0)}(n)\end{array}\right)$$

解方程得到最小二乘解为(7)：

$$\beta =(a,b{)}^T={\left(X^{T}X\right)}^{-1}{X}^T.Y$$

求解方程(3)得到GM(1,1)模型的离散解(8)：

$${\hat{x}}^{(1)}(k)=\left[x^{(0)}(1)-\frac{b}{a}\right]e^{-\alpha (k-1)}+\frac{b}{a}k=2,3,\cdots ,n$$

还原为原始数列，预测模型为(9)：

$${\hat{x}}^{(0)}(k)={\hat{x}}^{(1)}(k)-{\hat{x}}^{(1)}(k-1)k=2,3,4,\cdots ,n$$

将(8)带入(9)后得(10)：

$${\hat{x}}^{(0)}(k)=\left[x^{(0)}(1)-\frac{b}{a}\right]e^{-a(k-1)}\left(1-e^a\right)k=2,3,4,\cdots ,n$$

优点

1. 是灰色模型即使在少量数据情况下建立的模型,精度也会很高;
2. 是灰色模型从其机理上讲,越靠近当前时间点精度会越高,因此灰色模型的预测功能优于统计模型。

灰色系统建模实际上是一种以数找数的方法,从系统的一个或几个离散数列中找出系统的变化关系,试图建立系统的连续变化模型。

---

神经网络模型

多层前向神经网络原理介绍

多层前向神经网络(MLP)是神经网络中的一种，它由一些最基本的神经元即节点组成，如图

除输入层外，每一节点的输入为前一层所有节点输出值的和。每一节点的激励输出值由节点输入、激励函数及偏置量决定。

第$i$层为各节点的输入，通常需要归一化到-1和1之间。

在第$j$层，节点的输入值为：

$$ne{t}_j=\sum w_{ji}{o}_{\mathrm{i}}+{\theta }_{\mathrm{j}}$$

其中${\theta }_{\mathrm{j}}$为阈值，正阀值的作用将激励函数沿$x$轴向左平移
节点输出值为：$o_j=f\left(ne{t}_j\right)$
式子中$f$为节点的激励函数，通常选择如下$Sigmoid$函数：

$$f\left(x\right)=\frac{1}{1+\exp \left(-x\right)}$$
在第$k$层的网络节点输入为：$ne{t}_k=\sum w_{kj}{o}_j+{\theta }_k$
而输出为：$o_k=f\left(ne{t}_k\right)$
对每一个输入的模式样本$p$，平方误差$E_p$为：

$$E_p=\frac{1}{2}\sum _k{\left(t_{pk}-o_{pk}\right)}^2$$

在学习过程中，系统将调整连接权和阀值，使$E_p$尽可能快地下降。
全部学习样本总误差为：

$$E=\frac{1}{2p}\sum _p\sum _k{\left(t_{pk}-o_{pk}\right)}^2$$

$Matlab$相关函数介绍

网络初始化函数

$$net=newff\left(\left[x_m,x_M\right],\left[h_1,h_2,\cdots ,h_k\right],\left\{f_1,f_2,\cdots ,f_k\right\}\right)$$

$x_m$和$x_M$分别为列向量，存储各样本数据的最小值和最大值;第2个输入变量是一个行向量，输入各层节点数；第3个输入变量是字符串，代表该层的传输函数。常用

$$\tan sig\left(x\right)=\frac{1-e^{-2x}}{1+e^{-2x}},\mathrm{l}\mathrm{o}\mathrm{g}\sin \left(x\right)\frac{1}{1+e^{-x}}$$

还可以用设定参数Net.trainParam.epochs=1000
设定迭代次数
Net.trainFcn='traingm'设定带动量的剃度下降算法

网络训练函数

[net, tr, Y1, E1] = train(net, X, Y)
其中$X$为$n\times M$矩阵，$n$为输入变量的个数，$M$为样本数；$Y$为$m\times M$矩阵，$m$我输出变量的个数。$net$为返回后的神经网络对象，$tr$为训练跟踪数据，$tr.perf$为各步目标函数值。$Y1$为网络的最后输出，$E1$为训练误差向量。

网络泛化函数

Y2=sim(net, X1)
其中$X1$为输入数据矩阵，各列为样本数据。
$Y2$为对应输出值。

例题

例题一

函数拟合实验

产生函数在$[1,10]$上间隔为0.5的数据，利用神经网络学习，并推广到$[0,10]$上间隔为0.1上各点函数值。并分别作图。

$$y=0.2e^{-0.2x}+0.5e^{-0.15x}\sin \left(1.25x\right)$$

%%
clear, close, clc
tic

%%
x = 0 : 0.5 : 10;
y = 0.2 * exp(-0.2 * x) + 0.5 * exp(-0.15 * x) .* sin(1.25 * x);
net = newff([0, 10], [6, 1], {'tansig', 'tansig'});
net = train(net, x, y);
x1 = 0 : 0.1 : 10;
y1 = sim(net, x1);
plot(x, y, 'or',  x1, y1, 'b-')

%%
toc

例题二

有两种蠓Af和 Apf。根据它们的触角(mm)和翼长(mm)进行区分。现有9只Af和6只Apf。样本数据见表1和表2。

另有3只待判的蠓,触角和翼长数据为:(1.24,1.80),(1.28,1.84),(1.40,2.04)。试对它们进行判断。

这里我们可用三层神经网络进行判别。输入为15个二维向量，输出也为15个二维向量。其中Af对应的目标向量为(1,0)，Apf对应的目标向量为(0,1)。

%%
clear, close, clc
tic

%%
x=[1.24,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56,1.14,1.18,1.20,1.26,1.28,1.30
    1.72,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08,1.78,1.96,1.86,2.0, 2.0,1.96];
y=[1,1,1,1,1,1,1,1,1,0,0,0,0,0,0
    0,0,0,0,0,0,0,0,0,1,1,1,1,1,1];
net.trainParam.epochs = 2500;
xmin = min(x');
xmax = max(x');
net = newff([xmin', xmax'], [5, 2], {'logsig', 'logsig'});
net = train(net, x, y);
x1 = [1.24, 1.28, 1.40
    1.80, 1.84, 2.04];
y1 = sim(net, x1);
plot(x(1, 1:9),x(2, 1:9),'*',x(1, 10:15),x(2, 10:15),'o',x1(1,:),x1(2,:),'p')
legend('Af样本', 'Apf样本', '待分样本')
grid on

%%
toc

---

时间序列的典型分解模型

简介

一个时间序列的典型分解式为：

$$X_t=m_t+s_t+Y_t$$

其中$m_t$为趋势项，$s_t$是已知周期为$d$的周期项；$Y_t$是随机噪声项。

计算过程

设某周期性数据$X_{ij}\left(i=1,2,\cdots ,nj=1,2,\cdots ,12\right)$，共有$n$年数据，每年有12个数据，现对未来12个月进行预测。

提取季节项

求出第$i$年平均值：${\bar{X}}_i=\frac{{\sum }_{j=1}^{12}{X}_{ij}}{12}\left(i=1,2,\cdots ,n\right)$

对每个月数据零均值化：$s{t}_{ij}=X_{ij}-{\bar{X}}_i\left(i=1,2,\cdots ,nj=1,2,\cdots ,12\right)$

则季节项为：$S_i=\frac{{\sum }_{i=1}^{n}s{t}_{ij}}{n}\left(j=1,2,\cdots ,12\right)$

该$S_j$即为季节项，这里$T=12$。满足：$S_1+S_2+\cdots ,S_{12}=0$

获取去掉季节项后数据

$Y_{ij}=X_{ij}-S_j\left(i=1,2,\cdots ,nj=1,2\cdots ,12\right)$

将所有数据按行拉直变为一行

$$Z=Y=\left(Y_{1,1},Y_{1,2},\cdots ,Y_{1,12},Y_{2,1},Y_{2,2},\cdots ,Y_{2,12},\cdots ,Y_{n,1},Y_{n,2},\cdots Y_{n,12}\right)=\left(z_1,z_2,\cdots ,z_{12\times n}\right)$$

回归拟合

对数据$z_1,z_2,\cdots ,z_{12\times n}$才用多项式拟合，如一次多项式或者二次多项式。如设回归结果为$z_t=a+bt\left(t=1,2,\cdots ,12\times n\right)$

预测

对消除季节项后未来12个月预测值为${\hat{z}}_{12n+1},{\hat{z}}_{12n+2},\cdots ,{\hat{z}}_{12n+12}$。即${\hat{Y}}_{n+1,1},{\hat{Y}}_{n+1,2},\cdots ,{\hat{Y}}_{n+1,12}$则原始数据中未来12个月预测值为：

$${\hat{X}}_{n+1,j}={\hat{Y}}_{n+1,j}+S_j\left(j=1,2,\cdots ,12\right)$$

例题

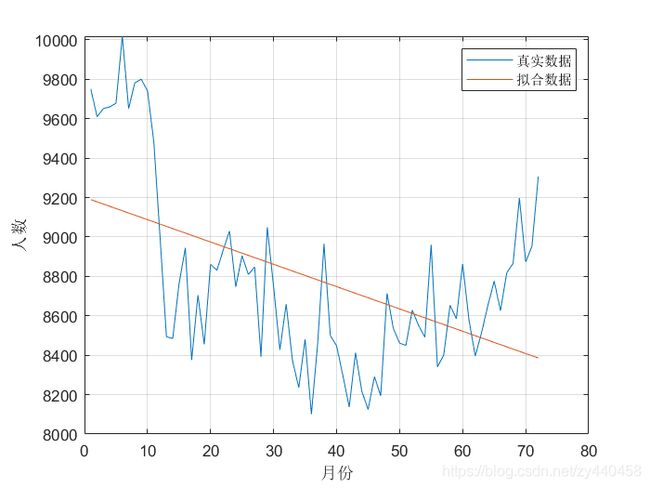
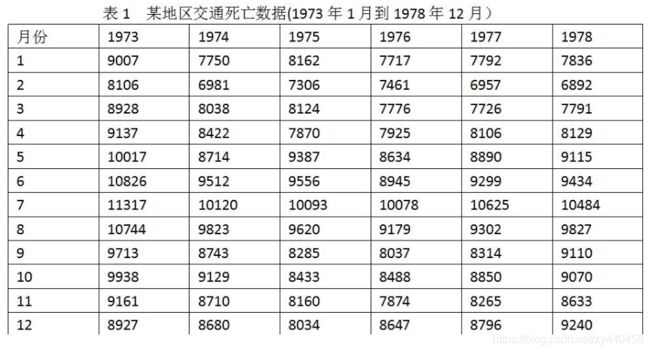
根据某地6年每年12个月的交通死亡数据。预测未来一年每个月的交通死亡人数

代码

%%
clear, close, clc
tic

%% 6年数据
X=[9007,8106,8928,9137,10017,10826,11317,10744,9713,9938,9161,8927
7750,6981,8038,8422,8714,9512,10120,9823,8743,9129,8710,8680
8162,7306,8124,7870,9387,9556,10093,9620,8285,8433,8160,8034
7717,7461,7776,7925,8634,8945,10078,9179,8037,8488,7874,8647
7792,6957,7726,8106,8890,9299,10625,9302,8314,8850,8265,8796
7836,6892,7791,8129,9115,9434,10484,9827,9110,9070,8633,9240];
[n, ~] = size(X);
N = n * 12;

%% 提取季节项
meanX = mean(X, 2); % 求出第i年平均值
st = X - meanX; % 对每个月数据零均值化
S = sum(st) / n;% 季节项

%% 获取去掉季节项后数据
Y = X - S;
tmp = Y';
Z = tmp(:); % 将所有数据按行拉直为一列

%% 回归拟合
p = polyfit(1 : N, Z', 1);
fun = polyval(p, 1 : N);
figure
plot(1 : N, Z, 1 : N, fun)
grid on
legend('真实数据', '拟合数据')
xlabel('月份'), ylabel('人数')

%% 预测
% 原始数据中未来12个月预测值
N1 = (n + 1) * 12;
fun1 = polyval(p, 1 : N1);
z = fun1(N + 1: end);
x = z + S;
tmpX = X';
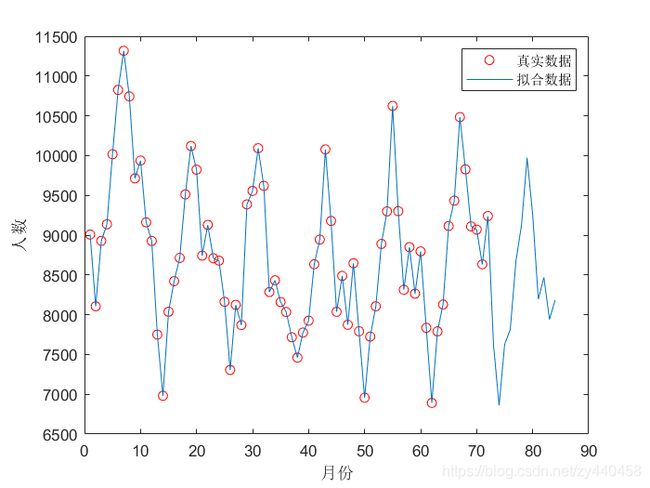
figure
plot(1 : N, tmpX(:), 'ro')
hold on
plot(1 : N1, [tmpX(:); x']);
legend('真实数据', '拟合数据')
xlabel('月份'), ylabel('人数')

%%
toc

---

插值与拟合模型

函数

一维插值函数interp1（）

调用方法：yi=interp1(x,y,xi,’methed’)
其中 x,y为插值点，yi为被插值点xi处的插值结果；x,y均为向量。’methed’表示采用的插值方法，MATLAB主要提供的方法有：‘nearest’最邻近差值；‘linear’线性插值；‘spline’三次样条插值；‘cubic’立方插值。缺省时表示线性插值。

水道测量问题

例题1

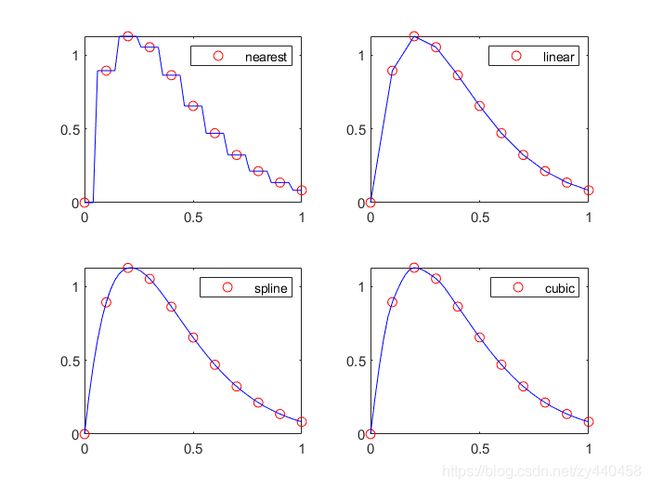
作函数$y=\left(x^2-3x+7\right)\cdot e^{-4x}\cdot \sin (2x)$在$[0,1]$取间隔为0.1得点图，用插值进行验证

%%
clear, close, clc
tic

%%
x = 0 : 0.1 : 1;
y = (x .^ 2 - 3 * x + 7) .* exp(-4 * x) .* sin(2 * x);
xx = 0 : 0.02 : 1;
yy1 = interp1(x, y, xx, 'nearest');
yy2 = interp1(x, y, xx, 'linear');
yy3 = interp1(x, y, xx, 'spline');
yy4 = interp1(x, y, xx, 'cubic');
subplot(2, 2, 1)
plot(x, y, 'ro', xx, yy1, 'b')
legend('nearest')
subplot(2, 2, 2)
plot(x, y, 'ro', xx, yy2, 'b')
legend('linear')
subplot(2, 2, 3)
plot(x, y, 'ro', xx, yy3, 'b')
legend('spline')
subplot(2, 2, 4)
plot(x, y, 'ro', xx, yy4, 'b')
legend('cubic')

%%
toc

例题2

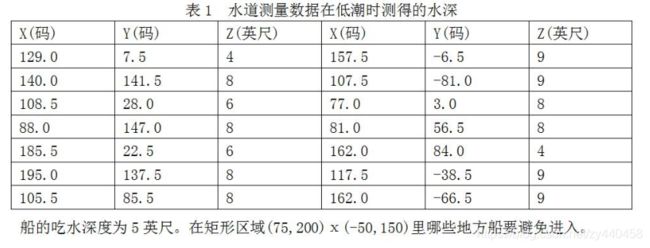
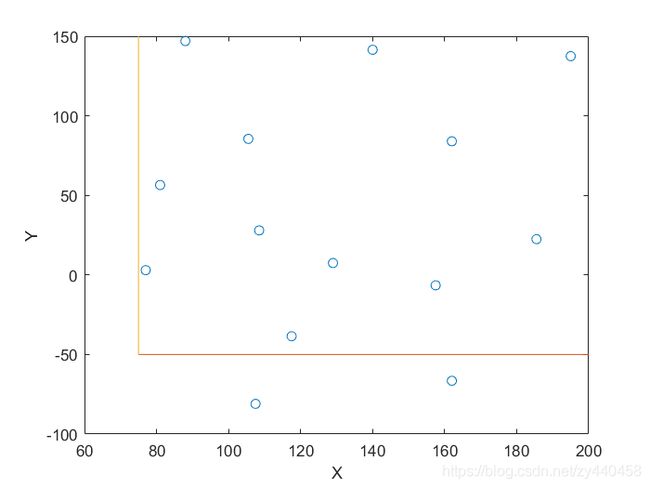
(MCM86A)）表1给出了在以码(1码=0.914米)为单位的直角坐标为X，Y的水面一点处以英尺（1英尺=0.3048米）计的水深Z。水深数据是在低潮时测得的。

水道离散点平面图

%%
clear, close, clc
tic

%%
data=[129.0,7.5,4
    140.0,141.5,8
    108.5,28.0,6
    88.0,147.0,8
    185.5,22.5,6
    195.0,137.5,8
    105.5,85.5,8
    157.5,-6.5,9
    107.5,-81.0,9
    77.0,3.0,8
    81.0,56.5,8
    162.0,84.0,4
    117.5,-38.5,9
    162.0,-66.5,9];
figure
plot(data(:, 1), data(:, 2), 'o', [75 200], [-50 -50], [75 75], [-50 150])
xlabel('X'), ylabel('Y')


%%
toc

所给14个点平面散点图，其中有两点不在区域

反距离权重法(IDW)算法

设有$n$个点$\left(x_i,y_i,z_i\right)$，计算平面上任意点$(x,y)$的$z$值。
$$z=\sum _{i=1}^n{w}_i{z}_i$$

其中权重

$$w_i=\frac{1/d_i^p}{{\sum }_{i=1}^{n}1/d_i^p},d_i=\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}$$

当$p$越大，则当插值点与给定点越近，相对作用越大，越远，相对作用越小。$p$通常取2

%%
clear, close, clc
tic

%%
data=[129.0,7.5,4
    140.0,141.5,8
    108.5,28.0,6
    88.0,147.0,8
    185.5,22.5,6
    195.0,137.5,8
    105.5,85.5,8
    157.5,-6.5,9
    107.5,-81.0,9
    77.0,3.0,8
    81.0,56.5,8
    162.0,84.0,4
    117.5,-38.5,9
    162.0,-66.5,9];
[X, Y] = meshgrid(75 : 0.1 : 200, -50 : 1 : 150);
p = 3;
d = zeros(length(data), 1);
w = zeros(length(data), 1);
Z = zeros(size(X));
count = 0;
for i = 1 : size(X, 1)
    for j = 1 : size(X, 2)
        for k = 1 : length(data)
            d(k) = sqrt((X(i, j) - data(k, 1)) .^ 2 + (Y(i, j) - data(k, 2)) .^ 2); % 插值点到各已知各点距离
            w(k) = 1.0 / d(k) ^ p; % 各点权重
        end
        w = w / sum(w); % 权值归一化
        z = sum(data(:, 3) .* w);
        Z(i, j) = -z;
        if z <= 5
            count = count + 1;
            D(count, 1) = X(i, j); D(count, 2) = Y(i, j);
        end
    end
end
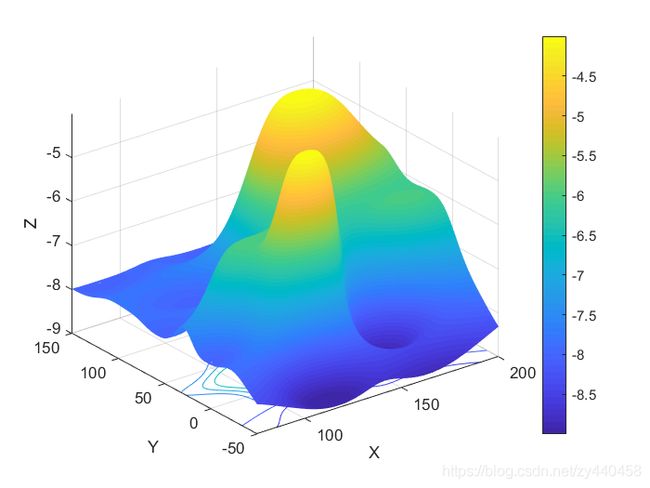
figure
surfc(X, Y, Z)
xlabel('X'), ylabel('Y'), zlabel('Z')
shading interp
colorbar
figure
contourf(X, Y, Z)
xlabel('X'), ylabel('Y')
colorbar
figure
contour(X,Y,Z)
hold on
plot(D(:, 1), D(:, 2), '*')
xlabel('X'), ylabel('Y')
%%
toc

---

水塔流量问题

题目描述

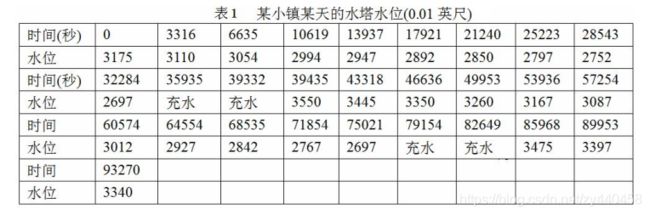
（MCM91A）美国某洲的各用水管理机构要求各社区提供以每小时多少加仑计的用水率以及每天总的用水量,但许多社区并没有测量水流入或流出水塔水量的设备,他们只能每小时测量水塔中的水位,精度在0.5%以内,更为重要的是,无论什么时候,只要水塔中的水位下降到某一最低水位L时,水泵就启动向水塔重新充水至某一最高水位H,但也无法得到水泵的供水量的测量数据。水泵每天向水塔充水一次或两次，每次约两小时。

1. 水塔是一个垂直圆形柱体，高为40英尺，直径57英尺。
2. 当水塔的水位降至27.00英尺时开始向水塔充水，
3. 当水位升至35.50英尺时停止充水。

试估计在任何时刻，甚至包括水泵正在工作期间内，水从水塔流出的流量f(t)，并估计一天的总用水量，表1中给出了某个真实小镇某一天的真实数据。

---

指标合成的客观权重方法

数据预处理

统计数据的指标介绍

为全面反映各高校实际情况，选取了包括人才培养、科学研究及成果方面的18个指标。这18个指标具体为:$X_1$授予博士学位，$X_2$授予硕士学位，$X_3$优博入选数，$X_4$发明专利数，$X_5$实用新型专利数，$X_6$国家一等奖励，$X_7$国家二等奖励数量，$X_8$国家社科基金项目奖一等数量，$X_9$国家社科基金项目奖二等数量，$X_{10}$国家社科基金项目奖三等数量，$X_{11}$教育部人文社科奖一等数量，$X_{12}$教育部人文社科奖二等数量，$X_{13}$教育部人文社科奖三等数量，$X_{14}$国家基地总数和国家重点学科(国家重点实验室、国家工程研究中心、人文社科基地数之和)，$X_{15}$经费总数(万元),$X_{16}$SCI总数，$X_{17}$E1总数，$X_{18}$CSCD、CSSCI总数。

数据的归一化处理

由于各个指标的取值范围不同，量纲与意义不同，为消除这些影响，需要对数据进行归一化处理。
设共有$n$个学校，每个学校共有$m$个指标，采集到的观测数据为：$x_{ij}\left(i=1,2,\cdots ,n;j=1,2,\cdots ,m\right)$，每个数值显然越大对排名越有利，因此归一化处理方法可以采用下式：

$$y_{ij}=\frac{x_{ij}-x_{jm}^{\ast }}{x_{jM}^{\ast }-x_{jm}^{\ast }}(i=1,2,\cdots ,n;j=,2,\cdots ,m)$$

其中：
$$x_{jM}^{\ast }=\underset{1\le i\le n}{\max }{x}_{ij},x_{jm}^{\ast }=\underset{1\le i\le n}{\min }{x}_{ij}$$

经过上面变化，所有数据都变到$[0,1]$，便于后续工作进行统一处理

客观权重确定的三种方法

熵权法

设$n$个学校的$m$个指标已经归一化处理，数据为：$y_{ij}\left(i=1,2,\cdots ,n;j=1,2,\cdots ,m\right)$其第$j$项指标的信息熵计算公式为：

$$E_j=-\frac{{\sum }_{i=1}^n{p}_{ij}\ln p_{ij}}{\ln n}j=1,2,\cdots ,m$$

$0⩽E_j⩽1$其中$p_{ij}=\frac{y_{ij}}{{\sum }_{i=1}^n{y}_{ij}}$，若$p_{ij}=0$，则定义$p_{ij}\ln p_{ij}=0$
$E_i$越小，表明数据间差异越大，因此提供的信息越大，该指标权重就越大；$E_j$越大，表明数据间彼此越接近，因此提供的信息越少，该指标权重就越小。
客观权重计算公式：
$$W_j=\frac{1-E_j}{m-{\sum }_{j=1}^m{E}_j}j=1,2,\cdots ,m$$

标准离差法

如果某个指标的标准差大，因此提供的信息越大，该指标权重就越大;反之，某个指标的标准差小，因此提供的信息越少，该指标权重就越小。利用标准差来计算各指标的客观权重，其计算式为:
$$W_j=\frac{{\sigma }_j}{{\sum }_{j=1}^m{\sigma }_j}j=1,2,\cdots ,m$$

CRITIC法确定权重

CRITIC法是Diakoulaki提出的一种客观赋权方法，确定权值以两个基本概念为基础：一是对比度，标准差越大权重相对越大。二是评价指标间的冲突性，当两个指标间有较强的正相关，说明两个指标冲突性低，两个指标反映的信息具有较大的相似性；当两个指标间有较强的负相关，说明两个指标冲突性大，两个指标反映的信息具有较大的不同。
确定第$j$个指标包含的信息量为：
$$c_j={\sigma }_j\sum _{i=1}^m\left(1-r_{ij}\right)\left(j=1,2,\cdots ,m\right)$$
第$j$个指标权重为：
$$w_j=\frac{c_j}{{\sum }_{i=1}^m{c}_i}\left(j=1,2,\cdots ,m\right)$$