【跟李沐学AI学习笔记】数据操作

本文的来源是B站跟李沐学AI的视频。

机器学习用的最多的数据结构是N维数组。最简单的N维数组是一个0-d的标量，比如1.0，它可能表示一个物体的类别。1-d的数组称为向量，比如说[1.0, 2.7, 3.4]，它是一个特征向量，可能是一个被抽象成一行数字的样本。2-d的数组称为矩阵，比如说[[1.0, 2.7, 3.4][5.0, 0.2, 4.6][4.3, 8.5, 0.2]]，表示一个样本的特征矩阵，每一行表示一个样本，每一列表示样本不同的特征。3-d最简单的就是一张RGB图片（宽x行xRGB通道）。4-d比如说是一个RGB图片批量（批量大小x宽x高x通道），在深度学习中往往是一次读取一批图片。5-d比如说是一个视频批量（批量大小x时间x宽x高x通道）。

创建数组需要：1.形状：例如3x4矩阵。2.每个元素的数据类型：例如32位浮点数。3.每个元素的值，例如全是0，或者随机数。

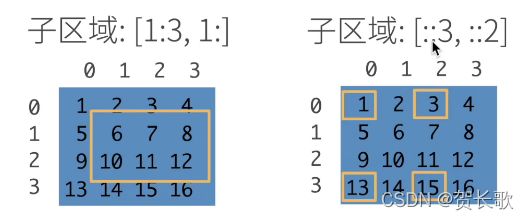
这里行和列都是从0开始的，第n行的意思是下标为n。一个元素：[1,2]。一行：[1,:]。一列：[:,1]。子区域：[1:3,1:]（这里是前闭后开，意思是第1行到第2行，从第1列到所有列）。子区域：[::3,::2]（跳着访问，从第0行到最后一行但是每3行一跳，即拿出第0行和第3行，从第0列到最后一列但是每2列一跳，就是拿出第0列和第2列。

  张量表示一个数值组成的数组，这个数组可能有多个维度。arange函数用于构造等差数组。 

>>> x=torch.arange(12)
>>> x
tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

   我们可能通过张量的shape属性来访问张量的形状和张量中元素的总数。

>>> x.shape
torch.Size([12])
>>> x.numel()
12

  numel(number of elements)是里面元素的种数 ，它永远是个标量。

  如果想改变一个张量的形状而不改变元素数量和元素值，可以调用reshape函数。

>>> x=x.reshape(3,4)
>>> x
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])

   使用全0、全1、其他常量或者从特定分布中随机采样的数字。

>>> torch.zeros((2,3,4))
tensor([[[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]],

        [[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]]])
>>> torch.ones((2,3,4))
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])

  通过提供包含数值的python列表（或嵌套列表）来为所需张量中的每个元素赋予确定值。

>>> torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])
tensor([[2, 1, 4, 3],
        [1, 2, 3, 4],
        [4, 3, 2, 1]])

常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。数组中使用浮点数来保证是按浮点数运算。**运算符是求幂。

>>> x=torch.tensor([1.0,2,4,8])
>>> y=torch.tensor([2,2,2,2])
>>> x+y,x-y,x*y,x/y,x**y
(tensor([ 3.,  4.,  6., 10.]), tensor([-1.,  0.,  2.,  6.]), tensor([ 2.,  4.,  8., 16.]), tensor([0.5000, 1.0000, 2.0000, 4.0000]), tensor([ 1.,  4., 16., 64.]))
>>> torch.exp(x)
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])

  我们也可以把多个张量连结在一起。dtype是数据类型对象。cat函数在第0维合并就是在行，可以理解成堆起来，在第1维合并就是按列。

>>> X=torch.arange(12,dtype=torch.float32).reshape(3,4)
>>> Y=torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
>>> torch.cat((X,Y),dim=0),torch.cat((X,Y),dim=1)
(tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [ 2.,  1.,  4.,  3.],
        [ 1.,  2.,  3.,  4.],
        [ 4.,  3.,  2.,  1.]]), tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
        [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
        [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))

  课程中李老师鼓励我们尝试一下对于3维张量，cat函数在0、1、2维的拼接表现。

>>> X=torch.tensor([[[2.0,1,4,3],[1,2,3,4],[4,3,2,1]],[[1,2,3,4],[4,3,2,1],[2,1,4,3]]])
>>> Y=torch.tensor([[[2.0,4,8,16],[4,8,16,2],[8,16,2,4]],[[1,3,5,7],[3,5,7,1],[5,7,1,3]]])
>>> torch.cat((X,Y),dim=0)
tensor([[[ 2.,  1.,  4.,  3.],
         [ 1.,  2.,  3.,  4.],
         [ 4.,  3.,  2.,  1.]],

        [[ 1.,  2.,  3.,  4.],
         [ 4.,  3.,  2.,  1.],
         [ 2.,  1.,  4.,  3.]],

        [[ 2.,  4.,  8., 16.],
         [ 4.,  8., 16.,  2.],
         [ 8., 16.,  2.,  4.]],

        [[ 1.,  3.,  5.,  7.],
         [ 3.,  5.,  7.,  1.],
         [ 5.,  7.,  1.,  3.]]])
>>> torch.cat((X,Y),dim=1)
tensor([[[ 2.,  1.,  4.,  3.],
         [ 1.,  2.,  3.,  4.],
         [ 4.,  3.,  2.,  1.],
         [ 2.,  4.,  8., 16.],
         [ 4.,  8., 16.,  2.],
         [ 8., 16.,  2.,  4.]],

        [[ 1.,  2.,  3.,  4.],
         [ 4.,  3.,  2.,  1.],
         [ 2.,  1.,  4.,  3.],
         [ 1.,  3.,  5.,  7.],
         [ 3.,  5.,  7.,  1.],
         [ 5.,  7.,  1.,  3.]]])
>>> torch.cat((X,Y),dim=2)
tensor([[[ 2.,  1.,  4.,  3.,  2.,  4.,  8., 16.],
         [ 1.,  2.,  3.,  4.,  4.,  8., 16.,  2.],
         [ 4.,  3.,  2.,  1.,  8., 16.,  2.,  4.]],

        [[ 1.,  2.,  3.,  4.,  1.,  3.,  5.,  7.],
         [ 4.,  3.,  2.,  1.,  3.,  5.,  7.,  1.],
         [ 2.,  1.,  4.,  3.,  5.,  7.,  1.,  3.]]])

  通过逻辑运算符构建二元张量。

>>> X==Y
tensor([[False,  True, False,  True],
        [False, False, False, False],
        [False, False, False, False]])

  对张量中的所有元素进行求和会产生一个只有一个元素的张量。

>>> X.sum()
tensor(66.)

  即使形状不同，仍然可以通过调用广播机制(broadcasting mechanism)来执行按元素操作。广播机制是指在满足特定限制的前提下，较小的数组“广播”至较大的数组，使两者形状相互容。这里非常容易出错，下例中a和b维度相同，故能使用该机制，a的列从1变为2，b的行从1变为3，进行相加运算。

>>> a=torch.arange(3).reshape((3,1))
>>> b=torch.arange(2).reshape((1,2))
>>> a,b
(tensor([[0],
        [1],
        [2]]), tensor([[0, 1]]))
>>> a+b
tensor([[0, 1],
        [1, 2],
        [2, 3]])

  可以用[-1]选择最后一个元素，可以用[1:3]选择第二个和第三个元素。

>>> X[-1],X[1:3]
(tensor([ 8.,  9., 10., 11.]), tensor([[ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.]]))

  除读取外，还可以通过指定索引来将元素写入矩阵。

>>> X[1,2]=9
>>> X
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  9.,  7.],
        [ 8.,  9., 10., 11.]])

  为多个元素赋值相同的值，只需要索引所有元素，然后为它们赋值。

  运用一些操作可能会导致为新结果分配内存。python的id是类似于c++指针的存在，它告诉你这个object在python中唯一的标识号。为Y赋值后，新的Y的id不等于之前的id。

>>> before=id(Y)
>>> Y=Y+X
>>> id(Y)==before
False

执行原地操作

>>> z=torch.zeros_like(Y)
>>> print('id(z):',id(z))
id(z): 2091821217168
>>> z[:]=X+Y
>>> print('id(z):',id(z))
id(z): 2091821217168

  如果在后续计算中没有重复使用X，也可以使用X[:]=X+Y或X+=Y来减少操作的内存开销。

>>> before=id(X)
>>> X+=Y
>>> id(X)==before
True

 Numpy是python中最常用的多元数组的框架。转换为numpy张量。

>>> A=x.numpy()
>>> B=torch.tensor(A)
>>> type(A),type(B)
(, )

  将大小为1的张量转换为python标量。a.item是一个numpy的浮点数。

>>> a=torch.tensor([3.5])
>>> a,a.item(),float(a),int(a)
(tensor([3.5000]), 3.5, 3.5, 3)