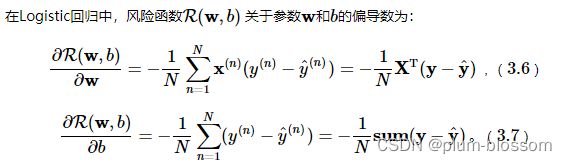NNDL 实验四 线性分类

前言

本篇文章是深度学习第四周的实验内容，主要使用pytorch来实现线性分类模型，二分类，多分类，并且利用softmax回归完成鸢尾花数据集分类任务，我们一起来学习吧(ง •_•)ง

pytorch实现

第3章 线性分类

3.1 基于Logistic回归的二分类任务

3.1.1 数据集构建

构建一个简单的分类任务，并构建训练集、验证集和测试集。
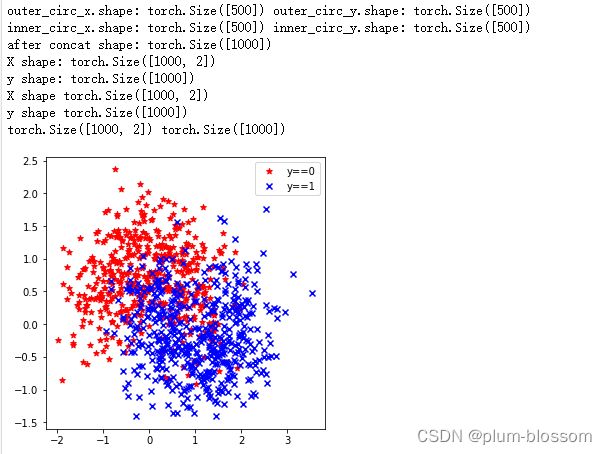
本任务的数据来自带噪音的两个弯月形状函数，每个弯月对一个类别。我们采集1000条样本，每个样本包含2个特征。

随机采集1000个样本，并进行可视化。

将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。

先导入后续需要使用的函数：

import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import torch
import math

生成弯月形状的函数代码如下：

def make_moons(n_samples=1000, shuffle=True, noise=None):
    """
    生成带噪音的弯月形状数据
    输入：
        - n_samples：数据量大小，数据类型为int
        - shuffle：是否打乱数据，数据类型为bool
        - noise：以多大的程度增加噪声，数据类型为None或float，noise为None时表示不增加噪声
    输出：
        - X：特征数据，shape=[n_samples,2]
        - y：标签数据, shape=[n_samples]
    """
    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out

    
    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))

    inner_circ_x = 1 - torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))
    
    print('outer_circ_x.shape:', outer_circ_x.shape, 'outer_circ_y.shape:', outer_circ_y.shape)
    print('inner_circ_x.shape:', inner_circ_x.shape, 'inner_circ_y.shape:', inner_circ_y.shape)
    
    # 使用'torch.concat'将两类数据的特征1和特征2分别延维度0拼接在一起，得到全部特征1和特征2
    # 使用'torch.stack'将两类特征延维度1堆叠在一起
    X = torch.stack(
        [torch.concat([outer_circ_x, inner_circ_x]),
        torch.concat([outer_circ_y, inner_circ_y])],
        axis=1
    )

    print('after concat shape:', torch.concat([outer_circ_x, inner_circ_x]).shape)
    print('X shape:', X.shape)

    # 使用'torch. zeros'将第一类数据的标签全部设置为0
    # 使用'torch. ones'将第一类数据的标签全部设置为1
    y = torch.concat(
        [torch.zeros(n_samples_out), torch.ones(n_samples_in)]
    )

    print('y shape:', y.shape)

    # 如果shuffle为True，将所有数据打乱
    if shuffle:
        # 使用'torch.randperm'生成一个数值在0到X.shape[0]，随机排列的一维Tensor做索引值，用于打乱数据
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
        print('X shape', X.shape)
        print('y shape', y.shape)

    # 如果noise不为None，则给特征值加入噪声
    if noise is not None:
        # 使用'torch.normal'生成符合正态分布的随机Tensor作为噪声，并加到原始特征上
        X += torch.normal(0, noise, size=X.shape)

    return X, y

随机采取1000个样本，，并进行可视化：

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)
# 可视化生产的数据集，不同颜色代表不同类别

print(X.shape, y.shape)

plt.figure(figsize=(5,5))
plt.scatter(x=X[:, 0][y==0], y=X[:, 1][y==0], marker='*', c='red', label='y==0')
plt.scatter(x=X[:, 0][y==1], y=X[:, 1][y==1], marker='x', c='blue', label='y==1')
plt.legend()
plt.show()

运行结果：

划分数据集：

由于在生成数据的时候已经进行过shuffle，在划分数据的时候不用再次打乱数据。

代码如下:

train_num = 640
eval_num = 160
test_num = 200

X_train, y_train = X[: train_num], y[: train_num]
X_eval, y_eval = X[train_num: train_num+eval_num], y[train_num: train_num+eval_num]
X_test, y_test = X[train_num+eval_num: ], y[train_num+eval_num: ]

y_train = y_train.reshape([-1, 1])
y_eval = y_eval.reshape([-1,1])
y_test = y_test.reshape([-1,1])

print('X_train.shape, y_train.shape', X_train.shape, y_train.shape)
print('X_eval.shape, y_eval.shape', X_eval.shape, y_eval.shape)
print('X_test.shape, y_test.shape', X_test.shape, y_test.shape)

运行结果：

3.1.2 模型构建

# 定义Logistic函数
def logistic(x):
    return 1 / (1 + torch.exp(-x))

# 绘制logistic函数图像
# 在[-10,10]的范围内生成一系列的输入值，用于绘制函数曲线
x = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(x, logistic(x), color="#e4007f", label="Logistic Function")
# 设置坐标轴
ax = plt.gca()
# 取消右侧和上侧坐标轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 设置默认的x轴和y轴方向
ax.xaxis.set_ticks_position('bottom') 
ax.yaxis.set_ticks_position('left')
# 设置坐标原点为(0,0)
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
# 添加图例
plt.legend()
plt.savefig('linear-logistic.pdf')
plt.show()

运行结果：

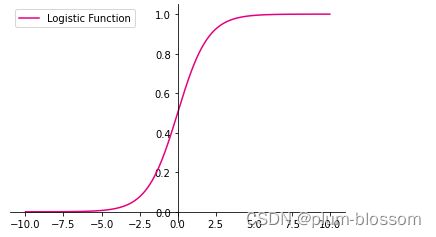
从输出结果看，当输入在0附近时，Logistic函数近似为线性函数；而当输入值非常大或非常小时，函数会对输入进行抑制。输入越小，则越接近0；输入越大，则越接近1。正因为Logistic函数具有这样的性质，使得其输出可以直接看作为概率分布。

Logistic回归算子

class model_LR(Op):
    def __init__(self, input_dim):
        super(model_LR, self).__init__()
        self.params = {}
        # 将线性层的权重参数全部初始化为0
        self.params['w'] = torch.zeros([input_dim, 1])
        # self.params['w'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, 1])
        # 将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros([1])

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D], N是样本数量，D为特征维度
        输出：
            - outputs：预测标签为1的概率，shape=[N,1]
        """
        # 线性计算
        score = torch.matmul(inputs, self.params['w']) + self.params['b']
        # Logistic 函数
        outputs = logistic(score)
        return outputs

测试一下

随机生成3条长度为4的数据输入Logistic回归模型，观察输出结果。

# 固定随机种子，保持每次运行结果一致
torch.seed()
# 随机生成3条长度为4的数据
inputs = torch.randn([3,4])
print('Input is:', inputs)
# 实例化模型
model = model_LR(4)
outputs = model(inputs)
print('Output is:', outputs)

运行结果：

从输出结果看，模型最终的输出g(⋅)恒为0.5。这是由于采用全0初始化后，不论输入值的大小为多少，Logistic函数的输入值恒为0，因此输出恒为0.5。

问题1：Logistic回归在不同的书籍中，有许多其他的称呼，具体有哪些？你认为哪个称呼最好？

在李航的《统计学习方法(第二版)》中被称为逻辑斯蒂分布。
还有对数几率回归。
对数几率回归更好。对数几率函数，简称对率函数。从对数几率回归这个名字就能得知它采用了对数几率函数，比较清楚。

问题2：什么是激活函数？为什么要用激活函数？常见激活函数有哪些？

激活函数的定义：

激活函数，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。
激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。

为什么要使用激活函数：

把非线性特性引入到神经网络中。
如果不使用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

常见的激活函数：

Sigmoid函数：

图像如下：

它能够把输入的连续实值变换为0和1之间的输出。如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1。可以用来做二分类。

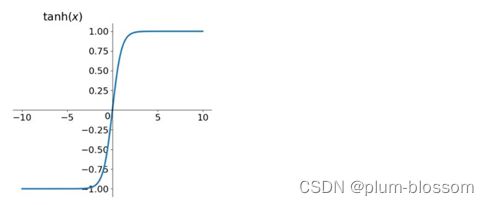
tanh函数

图像如下：

取值范围为[-1,1],
tanh在特征相差明显时效果会很好，在循环过程中会不断扩大特征效果，
tahn是0均值的，在实际应用中tanh比sigmoid更好。

relu函数
relu函数是一个取最大值函数，是目前最常用的激活函数

图像如下：

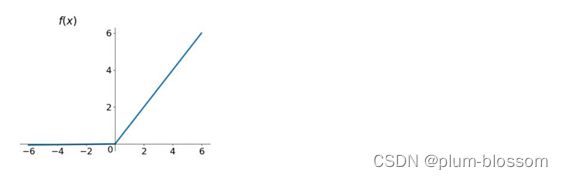
解决了在正区间梯度消失的问题
计算速度非常快，只需要判断输入是否大于0
收敛速度远快于sigmoid和tanh

softmax函数

通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。

3.1.3 损失函数

交叉熵损失函数

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self):
        self.predicts = None
        self.labels = None
        self.num = None

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts)) + torch.matmul((1-self.labels.t()), torch.log(1-self.predicts)))
        loss = torch.squeeze(loss, 1)
        return loss

# 测试一下
# 生成一组长度为3，值为1的标签数据
labels = torch.ones([3,1])
# 计算风险函数
bce_loss = BinaryCrossEntropyLoss()
print(bce_loss(outputs, labels))

运行结果：

3.1.4 模型优化

不同于线性回归中直接使用最小二乘法即可进行模型参数的求解，Logistic回归需要使用优化算法对模型参数进行有限次地迭代来获取更优的模型，从而尽可能地降低风险函数的值。
在机器学习任务中，最简单、常用的优化算法是梯度下降法。

使用梯度下降法进行模型优化，首先需要初始化参数W和 b，然后不断地计算它们的梯度，并沿梯度的反方向更新参数。

梯度下降：

class model_LR(Op):
    def __init__(self, input_dim):
        super(model_LR, self).__init__()
        # 存放线性层参数
        self.params = {}
        # 将线性层的权重参数全部初始化为0
        self.params['w'] = torch.zeros([input_dim, 1])
        # self.params['w'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, 1])
        # 将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros([1])
        # 存放参数的梯度
        self.grads = {}
        self.X = None
        self.outputs = None

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        self.X = inputs
        # 线性计算
        score = torch.matmul(inputs, self.params['w']) + self.params['b']
        # Logistic 函数
        self.outputs = logistic(score)
        return self.outputs

    def backward(self, labels):
        """
        输入：
            - labels：真实标签，shape=[N, 1]
        """
        N = labels.shape[0]
        # 计算偏导数
        self.grads['w'] = -1 / N * torch.matmul(self.X.t(), (labels - self.outputs))
        self.grads['b'] = -1 / N * torch.sum(labels - self.outputs)

参数更新：

from abc import abstractmethod

# 优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        """
        优化器类初始化
        """
        # 初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        # 指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        """
        定义每次迭代如何更新参数
        """
        pass

class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新

        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]

3.1.5 评价指标

在分类任务中，通常使用准确率（Accuracy）作为评价指标。

def accuracy(preds, labels):
    """
    输入：
        - preds：预测值，二分类时，shape=[N, 1]，N为样本数量，多分类时，shape=[N, C]，C为类别数量
        - labels：真实标签，shape=[N, 1]
    输出：
        - 准确率：shape=[1]
    """
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if preds.shape[1] == 1:
        # 二分类时，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
        # 使用'paddle.cast'将preds的数据类型转换为float32类型
        preds = torch.tensor(preds>=0.5, dtype=torch.float32)
    else:
        # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
        preds = torch.argmax(preds,axis=1, dtype='int32')
    return torch.mean(torch.tensor(torch.eq(preds, labels), dtype=torch.float32))

测试一下：

# 假设模型的预测值为[[0.],[1.],[1.],[0.]]，真实类别为[[1.],[1.],[0.],[0.]]，计算准确率
preds = torch.tensor([[0.],[1.],[1.],[0.]])
labels = torch.tensor([[1.],[1.],[0.],[0.]])
print("accuracy is:", accuracy(preds, labels))

运行结果：

3.1.6 完善Runner类

基于RunnerV1，本章的RunnerV2类在训练过程中使用梯度下降法进行网络优化，模型训练过程中计算在训练集和验证集上的损失及评估指标并打印，训练过程中保存最优模型。

# 用RunnerV2类封装整个训练过程
class RunnerV2(object):
    def __init__(self, model, optimizer, metric, loss_fn):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric
        # 记录训练过程中的评价指标变化情况
        self.train_scores = []
        self.dev_scores = []
        # 记录训练过程中的损失函数变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
        # 梯度打印函数，如果没有传入则默认为"None"
        print_grads = kwargs.get("print_grads", None)
        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y).item()
            self.train_loss.append(trn_loss)
            # 计算评价指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)
            # 计算参数梯度
            self.model.backward(y)
            if print_grads is not None:
                # 打印每一层的梯度
                print_grads(self.model)
            # 更新模型参数
            self.optimizer.step()
            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
            if epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}, loss: {trn_loss}, score: {trn_score}")
                print(f"[Dev] epoch: {epoch}, loss: {dev_loss}, score: {dev_score}")
                
    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评价指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_path):
        torch.save(self.model.params, save_path)

    def load_model(self, model_path):
        self.model.params = torch.load(model_path)

3.1.7 模型训练

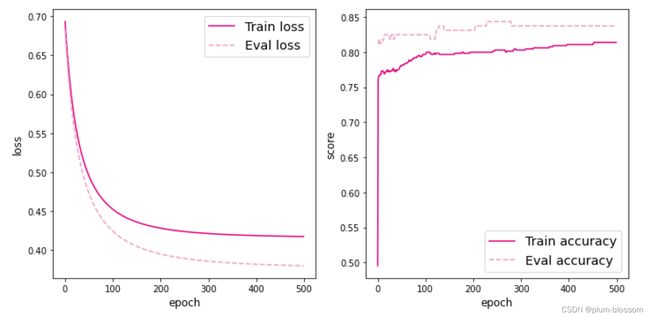
Logistic回归模型的训练，使用交叉熵损失函数和梯度下降法进行优化。
使用训练集和验证集进行模型训练，共训练 500个epoch，每隔50个epoch打印出训练集上的指标。

# 固定随机种子，保持每次运行结果一致
torch.seed()

# 特征维度
input_dim = 2
# 学习率
lr = 0.1

# 实例化模型
model = model_LR(input_dim=input_dim)
# 指定优化器
optimizer = SimpleBatchGD(init_lr=lr, model=model)
# 指定损失函数
loss_fn = BinaryCrossEntropyLoss()
# 指定评价方式
metric = accuracy

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_eval, y_eval], num_epochs=500, log_epochs=50, save_path="best_model")

运行结果：

3.1.8 模型评价

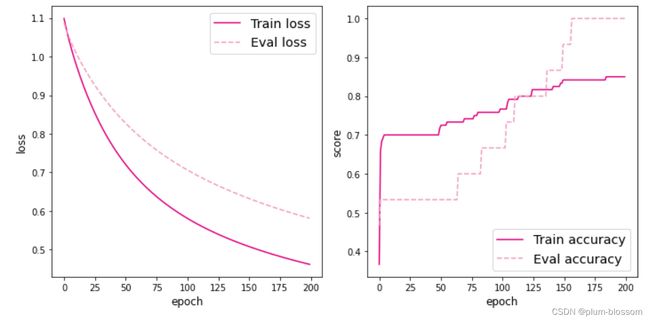
使用测试集对训练完成后的最终模型进行评价，观察模型在测试集上的准确率和loss数据。

# 可视化观察训练集与验证集的指标变化情况
def plot(runner,fig_name):
    plt.figure(figsize=(10,5))
    plt.subplot(1,2,1)
    epochs = [i for i in range(len(runner.train_scores))]
    # 绘制训练损失变化曲线
    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    # 绘制评价损失变化曲线
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Eval loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')
    plt.subplot(1,2,2)
    # 绘制训练准确率变化曲线
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    # 绘制评价准确率变化曲线
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Eval accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')
    plt.tight_layout()
    plt.savefig(fig_name)
    plt.show()

plot(runner,fig_name='linear-acc.pdf')

运行结果：

3.2 基于Softmax回归的多分类任务

Logistic回归可以有效地解决二分类问题。

但在分类任务中，还有一类多分类问题，即类别数C大于2 的分类问题。

Softmax回归就是Logistic回归在多分类问题上的推广。

3.2.1 数据集构建

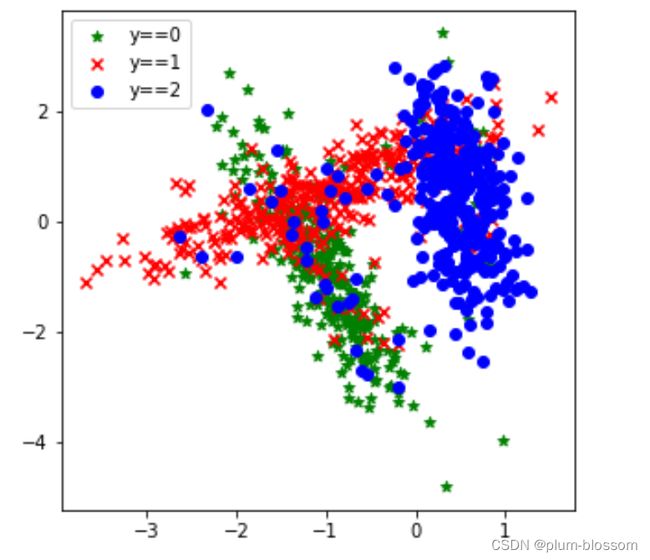
数据来自3个不同的簇，每个簇对一个类别。我们采集1000条样本，每个样本包含2个特征。

def make_multiclass_classification(n_samples=100, n_features=2, n_classes=3, shuffle=True, noise=0.1):
    """
    生成带噪音的多类别数据
    输入：
        - n_samples：数据量大小，数据类型为int
        - n_features：特征数量，数据类型为int
        - shuffle：是否打乱数据，数据类型为bool
        - noise：以多大的程度增加噪声，数据类型为None或float，noise为None时表示不增加噪声
    输出：
        - X：特征数据，shape=[n_samples,2]
        - y：标签数据, shape=[n_samples,1]
    """
    # 计算每个类别的样本数量
    n_samples_per_class = [int(n_samples / n_classes) for k in range(n_classes)]
    for i in range(n_samples - sum(n_samples_per_class)):
        n_samples_per_class[i % n_classes] += 1
    # 将特征和标签初始化为0
    X = torch.zeros([n_samples, n_features])
    y = torch.zeros([n_samples])
    # 随机生成3个簇中心作为类别中心
    centroids = torch.randperm(2 ** n_features)[:n_classes]
    centroids_bin = np.unpackbits(centroids.numpy().astype('uint8')).reshape((-1, 8))[:, -n_features:]
    centroids = torch.tensor(centroids_bin)
    # 控制簇中心的分离程度
    centroids = 1.5 * centroids - 1
    # 随机生成特征值
    X[:, :n_features] = torch.randn([n_samples, n_features])

    stop = 0
    # 将每个类的特征值控制在簇中心附近
    for k, centroid in enumerate(centroids):
        start, stop = stop, stop + n_samples_per_class[k]
        # 指定标签值
        y[start:stop] = k % n_classes
        X_k = X[start:stop, :n_features]
        # 控制每个类别特征值的分散程度
        A = 2 * torch.rand([n_features, n_features]) - 1
        X_k[...] = torch.matmul(X_k, A)
        X_k += centroid
        X[start:stop, :n_features] = X_k

    # 如果noise不为None，则给特征加入噪声
    if noise > 0.0:
        # 生成noise掩膜，用来指定给那些样本加入噪声
        noise_mask = torch.rand([n_samples]) < noise
        for i in range(len(noise_mask)):
            if noise_mask[i]:
                # 给加噪声的样本随机赋标签值
                y[i] = torch.randint(n_classes, [1])
    # 如果shuffle为True，将所有数据打乱
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]

    return X, y

# 固定随机种子，保持每次运行结果一致
torch.manual_seed(66)
# 采样1000个样本
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)

# 可视化生产的数据集，不同颜色代表不同类别
plt.figure(figsize=(5,5))
plt.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='*', color='green', label='y==0')
plt.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='x', color='red', label='y==1')
plt.scatter(X[:, 0][y==2], X[:, 1][y==2], color='blue', label='y==2')
plt.legend()
plt.savefig('linear-dataset-vis2.pdf')
plt.show()

运行结果：

划分数据集的方法和二分类任务相似。

3.2.2 模型构建

def softmax(X):
    """
    输入：
        - X：shape=[N, C]，N为向量数量，C为向量维度
    """
    x_max = torch.max(X, dim=1, keepdim=True)[0]  #N, 1
    x_exp = torch.exp(X - x_max)
    partition = torch.sum(x_exp, 1, keepdim=True) #N, 1
    return x_exp / partition

# 观察softmax的计算方式
X = torch.tensor([[0.1, 0.2, 0.3, 0.4],[1,2,3,4]])
predict = softmax(X)
print(predict)

运行结果：

class model_SR(Op):
    def __init__(self, input_dim, output_dim):
        super(model_SR, self).__init__()
        self.params = {}
        # 将线性层的权重参数全部初始化为0
        self.params['W'] = torch.zeros([input_dim, output_dim])
        # self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
        # 将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros([output_dim])
        self.outputs = None

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D], N是样本数量，D是特征维度
        输出：
            - outputs：预测值，shape=[N,C]，C是类别数
        """
        # 线性计算
        score = torch.matmul(inputs, self.params['W']) + self.params['b']
        # Softmax 函数
        self.outputs = softmax(score)
        return self.outputs

# 随机生成1条长度为4的数据
inputs = torch.randn([1,4])
print('Input is:', inputs)
# 实例化模型，这里令输入长度为4，输出类别数为3
model = model_SR(input_dim=4, output_dim=3)
outputs = model(inputs)
print('Output is:', outputs)

运行结果：

思考题：Logistic函数是激活函数。Softmax函数是激活函数么？谈谈你的看法。

softmax函数是激活函数，softmax函数可以让大的值更大，让小的更小，增加了区分对比度，学习效率更高。并且softmax是连续可导的，消除了拐点。

3.2.3 损失函数

class MultiCrossEntropyLoss(Op):
    def __init__(self):
        self.predicts = None
        self.labels = None
        self.num = None

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = 0
        for i in range(0, self.num):
            index = self.labels[i]
            loss -= torch.log(self.predicts[i][index])
        return loss / self.num

# 测试一下
# 假设真实标签为第1类
labels = torch.tensor([0])
# 计算风险函数
mce_loss = MultiCrossEntropyLoss()
print(mce_loss(outputs, labels))

运行结果：

3.2.4 模型优化

使用3.1.4.2中实现的梯度下降法进行参数更新

class model_SR(Op):
    def __init__(self, input_dim, output_dim):
        super(model_SR, self).__init__()
        self.params = {}
        # 将线性层的权重参数全部初始化为0
        self.params['W'] = torch.zeros([input_dim, output_dim])
        # self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
        # 将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros([output_dim])
        # 存放参数的梯度
        self.grads = {}
        self.X = None
        self.outputs = None
        self.output_dim = output_dim

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        self.X = self.params['W']
        # 线性计算
        score = torch.matmul(inputs, self.params['W']) + self.params['b']
        
        # Softmax 函数
        self.outputs = softmax(score)
        return self.outputs

    def backward(self, labels):
        N =labels.shape[0]
        labels = torch.nn.functional.one_hot(labels.to(torch.int64), self.output_dim)
        self.grads['W'] = -1 / N * torch.matmul(self.X.t(), (labels-self.outputs))
        self.grads['b'] = -1 / N * torch.matmul(torch.ones([N]), (labels-self.outputs))

3.2.5 模型训练

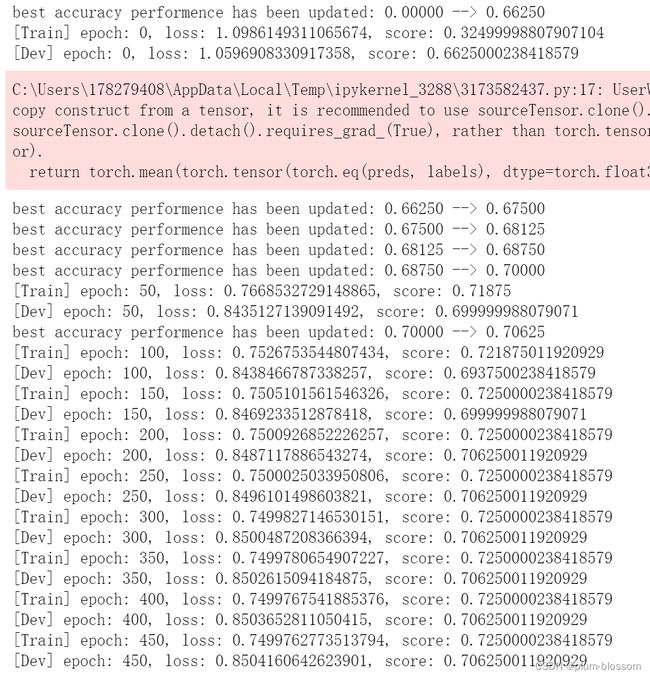
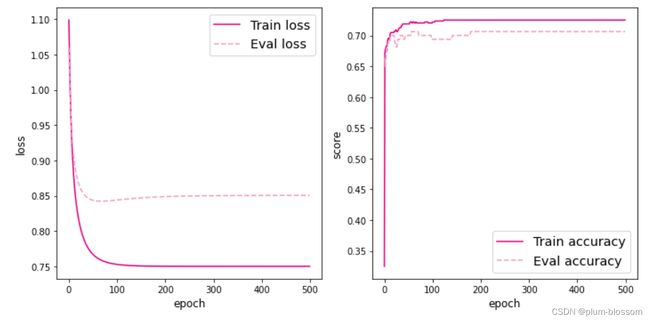
实例化RunnerV2类，并传入训练配置。使用训练集和验证集进行模型训练，共训练500个epoch。每隔50个epoch打印训练集上的指标。

# 固定随机种子，保持每次运行结果一致
torch.manual_seed(66)


# 特征维度
input_dim = 2
# 类别数
output_dim = 3
# 学习率
lr = 0.1

# 实例化模型
model = model_SR(input_dim=input_dim, output_dim=output_dim)
# 学习率
lr = 0.2

# 梯度下降法
optimizer = SimpleBatchGD(init_lr=lr, model=model)
# 交叉熵损失
loss_fn = MultiCrossEntropyLoss()
# 准确率
metric = accuracy

# 实例化RunnerV2
runner = RunnerV2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=500, log_epochs=50, save_path="best_model_mul")

             # 可视化观察训练集与验证集的准确率变化情况
plot(runner, fig_name='linear-acc2.pdf')
plt.show()

运行结果：

3.2.6 模型评价

使用测试集对训练完成后的最终模型进行评价，观察模型在测试集上的准确率。

# 加载最优模型
runner.load_model('best_model_mul')
# 模型评价
score, loss = runner.evaluate([X_test, y_test])

print('score/loss', score, loss)

运行结果：

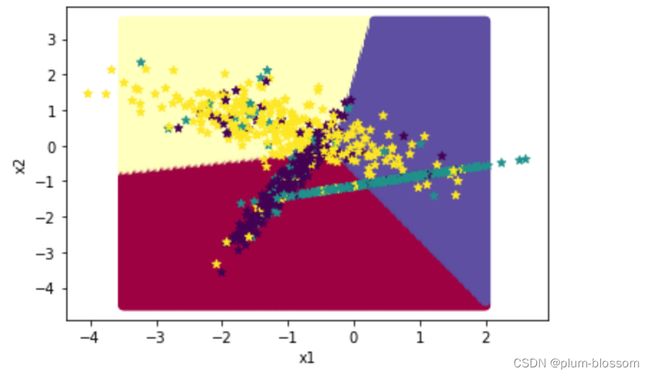
# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-3.5, 2, 200), torch.linspace(-4.5, 3.5, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)
# 预测对应类别
y = runner.predict(x)
y = torch.argmax(y, axis=1)
# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

torch.seed()
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)

plt.scatter(X[:, 0].tolist(), X[:, 1].tolist(), marker='*', c=y.tolist())
plt.show()

运行结果：

3.3 实践：基于Softmax回归完成鸢尾花分类任务

步骤：数据处理、模型构建、损失函数定义、优化器构建、模型训练、模型评价和模型预测等，

数据处理：根据网络接收的数据格式，完成相应的预处理操作，保证模型正常读取；
模型构建：定义Softmax回归模型类；
训练配置：训练相关的一些配置，如：优化算法、评价指标等；
组装Runner类：Runner用于管理模型训练和测试过程；
模型训练和测试：利用Runner进行模型训练、评价和测试。
（说明：使用深度学习进行实践时的操作流程基本一致，后文不再赘述。）

3.3.1 数据处理

3.3.1.1 数据集介绍

Iris数据集，也称为鸢尾花数据集，包含了3种鸢尾花类别（Setosa、Versicolour、Virginica），每种类别有50个样本，共计150个样本。其中每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度，本实验通过鸢尾花这4个属性来判断该样本的类别。

3.3.1.2 数据清洗

from sklearn.datasets import load_iris
import pandas
import numpy as np
import torch


iris_features = np.array(load_iris().data, dtype=np.float32)
iris_labels = np.array(load_iris().target, dtype=np.int32)
print(pandas.isna(iris_features).sum())
print(pandas.isna(iris_labels).sum())

运行结果：

import matplotlib.pyplot as plt #可视化工具

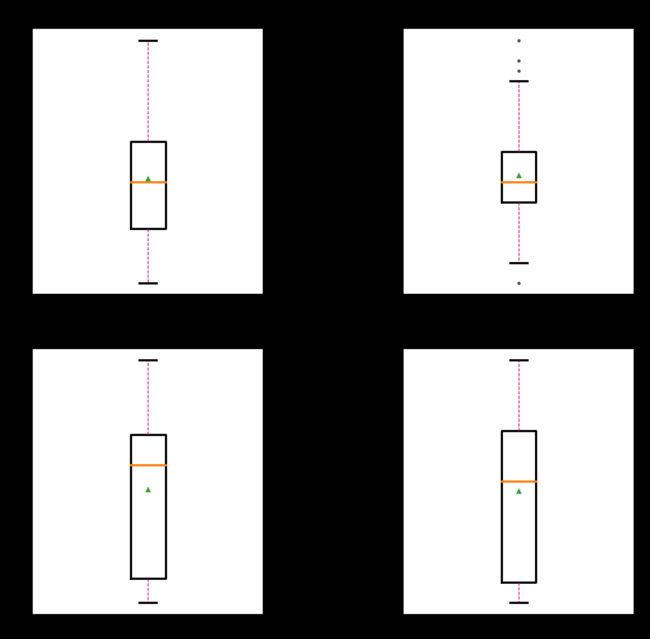
# 箱线图查看异常值分布
def boxplot(features):
    feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']

    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=200)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i in range(4):
        plt.subplot(2, 2, i+1)
        # 画箱线图
        plt.boxplot(features[:, i], 
                    showmeans=True, 
                    whiskerprops={"color":"#E20079", "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    meanprops={"markersize":1})
        # 图名
        plt.title(feature_names[i], fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig('ml-vis.pdf')
    plt.show()

boxplot(iris_features)
import matplotlib.pyplot as plt #可视化工具

# 箱线图查看异常值分布
def boxplot(features):
    feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']

    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=200)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i in range(4):
        plt.subplot(2, 2, i+1)
        # 画箱线图
        plt.boxplot(features[:, i], 
                    showmeans=True, 
                    whiskerprops={"color":"#E20079", "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    meanprops={"markersize":1})
        # 图名
        plt.title(feature_names[i], fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig('ml-vis.pdf')
    plt.show()

boxplot(iris_features)

运行结果：

3.3.2 数据集划分

# 加载数据集
def load_data(shuffle=True):
    """
    加载鸢尾花数据
    输入：
        - shuffle：是否打乱数据，数据类型为bool
    输出：
        - X：特征数据，shape=[150,4]
        - y：标签数据, shape=[150]
    """
    # 加载原始数据
    X = np.array(load_iris().data, dtype=np.float32)
    y = np.array(load_iris().target, dtype=np.int32)

    X = torch.tensor(X)
    y = torch.tensor(y)

    # 数据归一化
    X_min = torch.min(X, 0)[0]
    X_max = torch.max(X, 0)[0]
    X = (X-X_min) / (X_max-X_min)

    # 如果shuffle为True，随机打乱数据
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
    return X, y

# 固定随机种子
torch.manual_seed(66)

num_train = 120
num_dev = 15
num_test = 15

X, y = load_data(shuffle=True)
print("X shape: ", X.shape, "y shape: ", y.shape)
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
# 打印X_train和y_train的维度
print("X_train shape: ", X_train.shape, "y_train shape: ", y_train.shape)

运行结果：

3.3.3 模型构建

# 输入维度
input_dim = 4
# 类别数
output_dim = 3
# 实例化模型
model = model_SR(input_dim=input_dim, output_dim=output_dim)

3.3.4 模型训练

# 学习率
lr = 0.2

# 梯度下降法
optimizer = SimpleBatchGD(init_lr=lr, model=model)
# 交叉熵损失
loss_fn = MultiCrossEntropyLoss()
# 准确率
metric = accuracy

# 实例化RunnerV2
runner = RunnerV2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=200, log_epochs=10, save_path="best_model.pdparams")

运行结果：

可视化训练集和验证集：

plot(runner,fig_name='linear-acc3.pdf')

运行结果：

3.3.4 模型评价

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate([X_test, y_test])

print('score/loss', score, loss)

运行结果：

3.3.5 模型预测

# 预测测试集数据
logits = runner.predict(X_test)
# 观察其中一条样本的预测结果
pred = torch.argmax(logits[0]).numpy()
# 获取该样本概率最大的类别
label = y_test[0].numpy()
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred))

运行结果：

主要配置：

数据：Iris数据集；
模型：Softmax回归模型；
损失函数：交叉熵损失；
优化器：梯度下
降法；
评价指标：准确率。
为了加深对机器学习模型的理解，请自己动手完成以下实验：

3.4 模型调整

尝试调整学习率和训练轮数等超参数，观察是否能够得到更高的精度；

1、将学习率调整维0.1，训练次数增加至250

2、将学习率调整维0.18，训练次数增加至250

3、将学习率调整维0.01，训练次数增加至250

4、将学习率调整维0.001，训练次数增加至250

5、将学习率调整维0.2，训练次数增加至300

在解决多分类问题时，还有一个思路是将每个类别的求解问题拆分成一个二分类任务，通过判断是否属于该类别来判断最终结果。请分别尝试两种求解思路，观察哪种能够取得更好的结果；（选做）
尝试使用《神经网络与深度学习》中的其他模型进行鸢尾花识别任务，观察是否能够得到更高的精度。（选做）

总结

本篇文章主要利用Logistic回归完成二分类任务，利用softmax回归完成多分类回归，并且基于softmax完成鸢尾花数据集分类。在学习中更深的理解了可以利用调整学习率和训练参数来提高模型的准确率。