NNDL 作业5：卷积
文章目录
-
- 作业1 编程实现
-
-
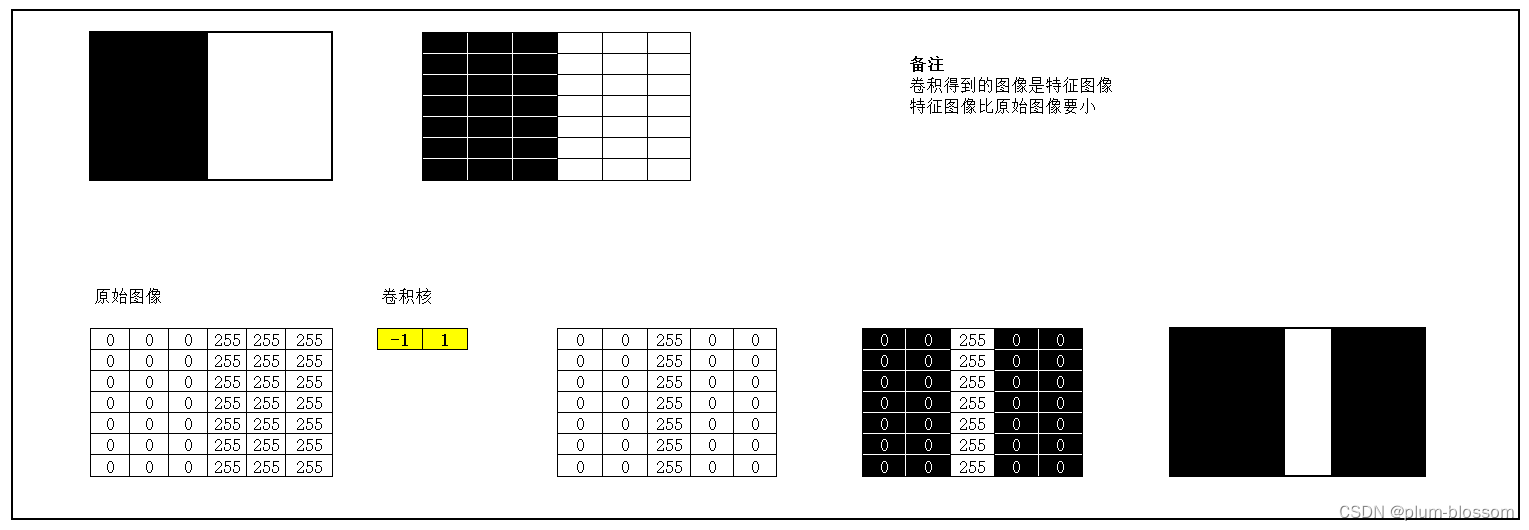
- 1.图1使用卷积核( 1 − 1 )，输出特征图
- 2. 图1使用卷积核( 1 − 1 )^T^，输出特征图
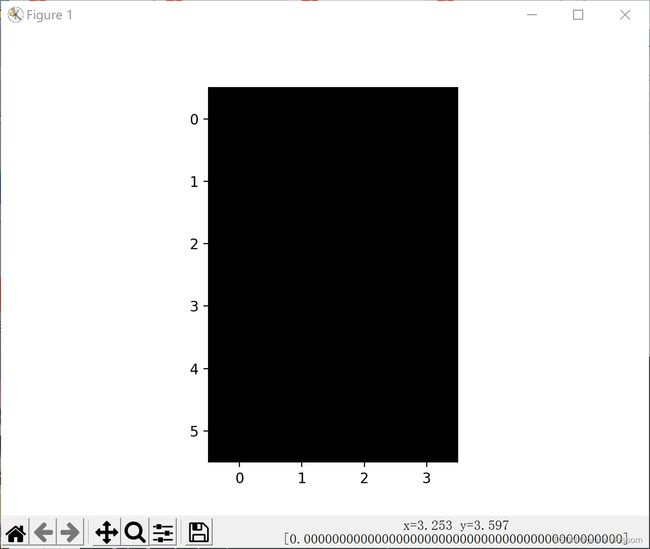
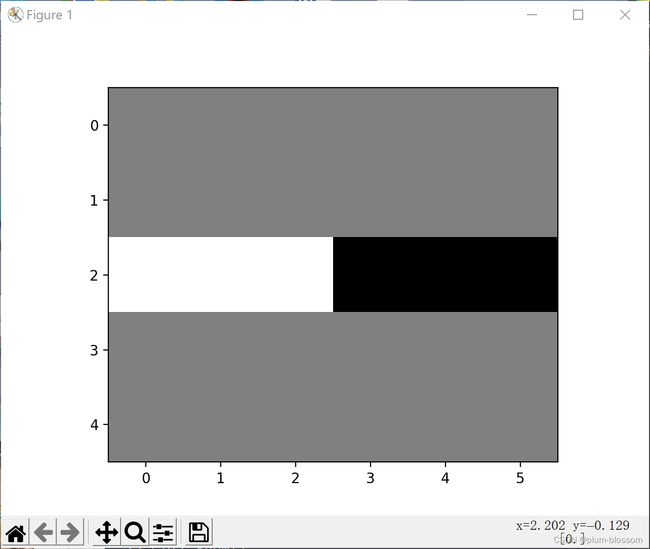
- 3. 图2使用卷积核( 1 − 1 )，输出特征图
- 4. 图2使用卷积核( 1 − 1 )^T^，输出特征图
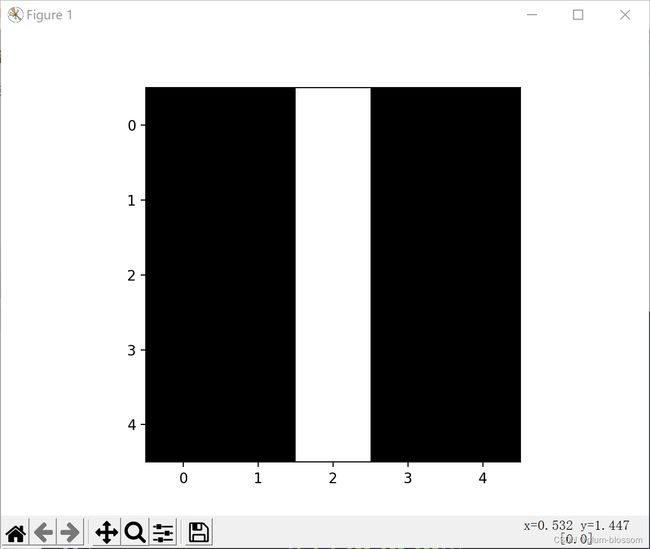
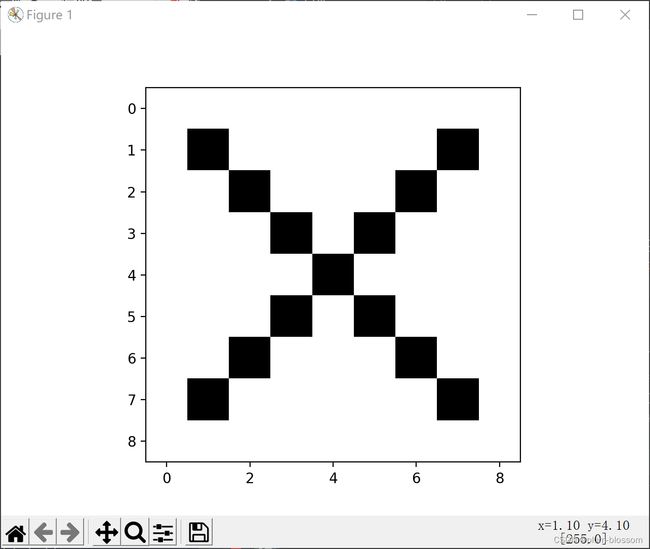
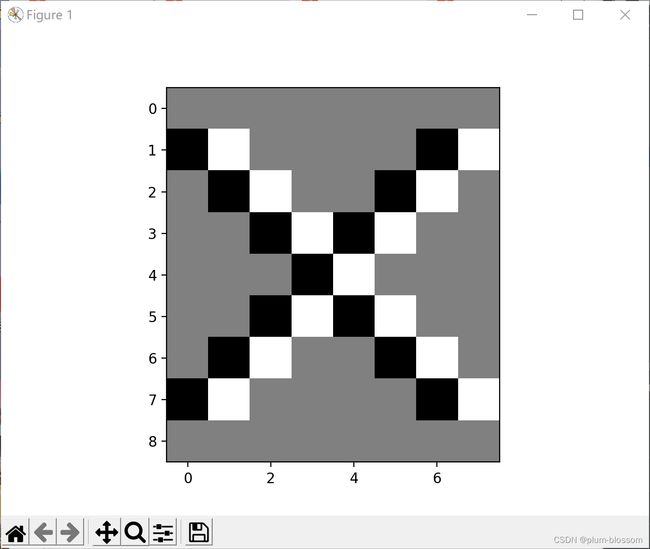
- 5. 图3使用卷积核( 1 − 1 )，(1 −1)^T^,
-
- 作业2
-
-
- 一、概念
- **卷积：**
- **卷积核：**
- **特征图：**
- **特征选择：**
- **步长：**
- **填充：**
- **感受野：**
- 二、探究不同卷积核的作用
- 三、编程实现
-
-
- 1.实现灰度图的边缘检测、锐化、模糊。（必做）
- 2.调整卷积核参数，测试并总结。（必做）
- 3.使用不同尺寸图片，测试并总结。（必做）
- 4.探索更多类型卷积核。（选做）
- 5.尝试彩色图片边缘检测。（选做）
-
-
- 总结
- 参考
卷积常用于 特征提取
作业1 编程实现
1.图1使用卷积核( 1 − 1 )，输出特征图
2. 图1使用卷积核( 1 − 1 )T，输出特征图
3. 图2使用卷积核( 1 − 1 )，输出特征图
4. 图2使用卷积核( 1 − 1 )T，输出特征图
5. 图3使用卷积核( 1 − 1 )，(1 −1)T,
输出特征图卷积核( 1 − 1 )
1.图1使用卷积核( 1 − 1 )，输出特征图
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
import numpy as np
#生成图片
def create_pic():
picture = torch.Tensor([[0,0,0,255,255,255],
[0,0,0,255,255,255],
[0,0,0,255,255,255],
[0,0,0,255,255,255],
[0,0,0,255,255,255]])
return picture
#确定卷积网络
class MyNet(torch.nn.Module):
def __init__(self,kernel,kshape):
super(MyNet, self).__init__()
kernel = torch.reshape(kernel,kshape)
self.weight = torch.nn.Parameter(data=kernel, requires_grad=False)
def forward(self, picture):
picture = F.conv2d(picture,self.weight,stride=1,padding=0)
return picture
#确定卷积层
kernel = torch.tensor([-1.0,1.0])
#更改卷积层的形状适应卷积函数
kshape = (1,1,1,2)
#生成模型
model = MyNet(kernel=kernel,kshape=kshape)
#生成图片
picture = create_pic()
#更改图片的形状适应卷积层
picture = torch.reshape(picture,(1,1,5,6))
output = model(picture)
output = torch.reshape(output,(5,5))
plt.imshow(output,cmap='gray')
plt.show()
运行结果：
2. 图1使用卷积核( 1 − 1 )T，输出特征图
kernel = torch.tensor([-1.0,1.0])
#更改卷积和的形状为转置
kshape = (1,1,2,1)
model = MyNet(kernel=kernel,kshape=kshape)
picture = create_pic()
picture = torch.reshape(picture,(1,1,5,6))
output = model(picture)
output = torch.reshape(output,(6,4))
plt.imshow(output,cmap='gray')
plt.show()
运行结果：
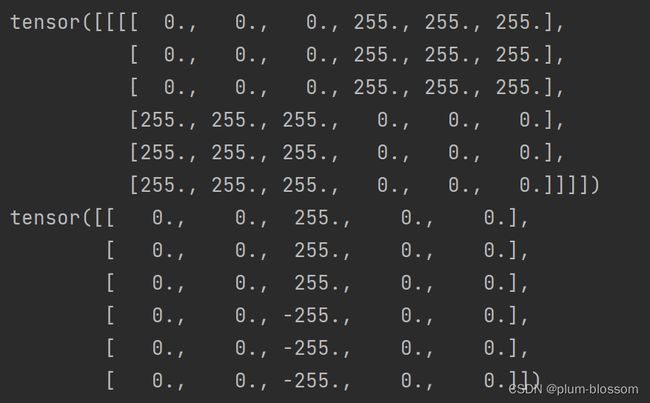
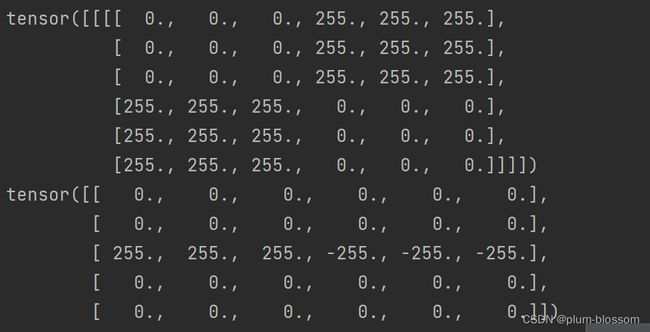
3. 图2使用卷积核( 1 − 1 )，输出特征图
#生成图像
def create_pic():
picture = torch.Tensor([[0,0,0,255,255,255],
[0,0,0,255,255,255],
[0,0,0,255,255,255],
[255,255,255,0,0,0],
[255,255,255,0,0,0],
[255,255,255,0,0,0]])
return picture
#确定卷积核
kernel = torch.tensor([-1.0,1.0])
kshape = (1,1,1,2)
#生成模型
model = MyNet(kernel=kernel,kshape=kshape)
picture = create_pic()
picture = torch.reshape(picture,(1,1,6,6))
print(picture)
output = model(picture)
output = torch.reshape(output,(6,5))
print(output)
plt.imshow(output,cmap='gray')
plt.show()
运行结果：
4. 图2使用卷积核( 1 − 1 )T，输出特征图
kernel = torch.tensor([-1.0,1.0])
kshape = (1,1,2,1)
model = MyNet(kernel=kernel,kshape=kshape)
picture = create_pic()
picture = torch.reshape(picture,(1,1,6,6))
print(picture)
output = model(picture)
output = torch.reshape(output,(5,6))
print(output)
plt.imshow(output,cmap='gray')
plt.show()
运行结果：
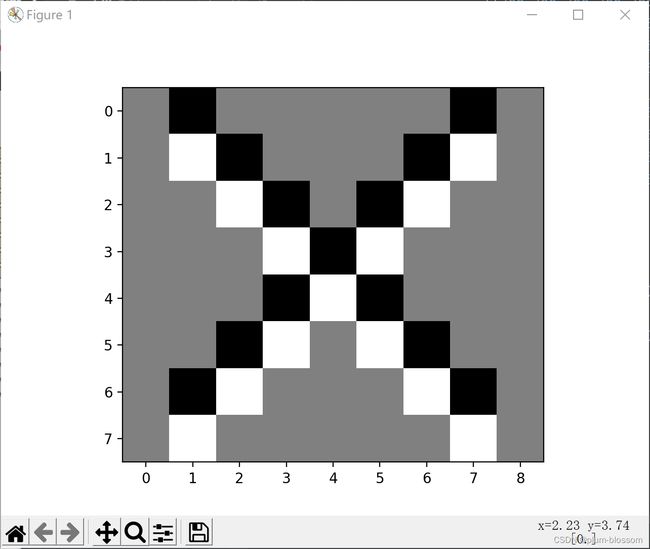
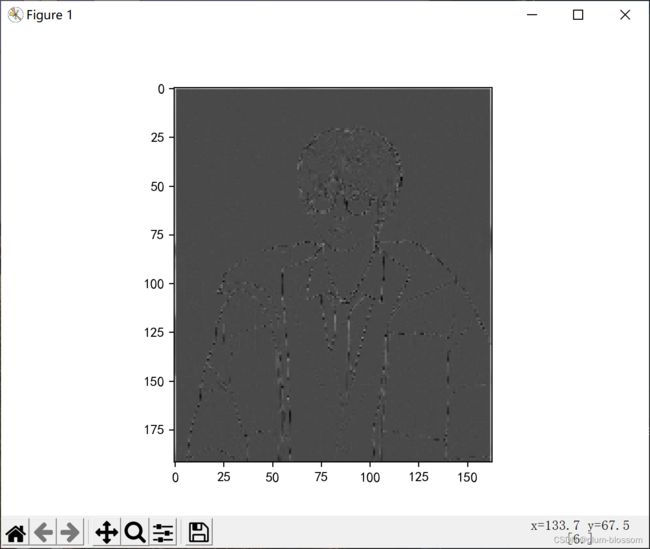
5. 图3使用卷积核( 1 − 1 )，(1 −1)T,
生成的原图：
卷积核( 1 − 1 )
卷积核(1 −1)T
卷积核
作业2
一、概念
用自己的语言描述“卷积、卷积核、特征图、特征选择、步长、填充、感受野”。
卷积：
卷积是指在滑动中提取特征的过程，可以形象地理解为用放大镜把每步都放大并且拍下来，再把拍下来的图片拼接成一个新的大图片的过程。
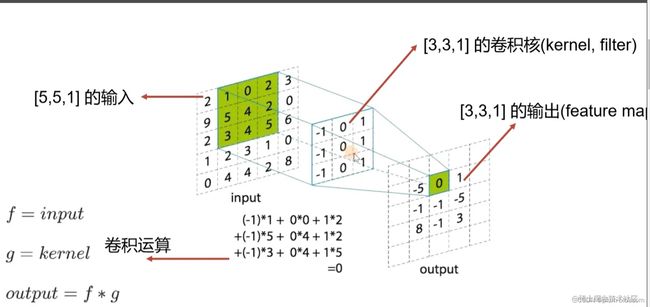
卷积操作后得到的矩阵中的每个元素都是由两个矩阵乘积得来的——这两个矩阵分别是【原矩阵在滑动过中分割出来的“大小等同于卷积核”的矩阵】和【卷积核（卷积核一般是一个3×3或者5×5的矩阵）】
卷积核：
- 卷积是为了提取特征，选择不同的卷积核将会提取到不同的特征。
- 卷积核：模型待优化的参数
特征图：
- 特征图（feature map）：在每个卷积层，数据都是以三维形式存在的。你可以把它看成许多个二维图片叠在一起，其中每一个称为一个feature map。在输入层，如果是灰度图片，那就只有一个feature map；如果是彩色图片，一般就是3个feature map（红绿蓝）。层与层之间会有若干个卷积核（kernel），上一层和每个feature map跟每个卷积核做卷积，都会产生下一层的一个feature map。
特征选择：
- 特征选择的目的：在实际项目中，我们可能会有大量的特征可使用，有的特征携带的信息丰富，有的特征携带的信息有重叠，有的特征则属于无关特征，如果所有特征不经筛选地全部作为训练特征，经常会出现维度灾难问题，甚至会降低模型的准确性，如果只选择所有特征中的关键特征构建模型，那么可以大大减少学习算法的运行时间，也可以增加模型的可解释性。
步长：
-
步长（stride）：保留相邻区域特征的相关性
-
在卷积层中，有时我们会需要一个尺寸小于输入的输出
-
当通道数量增加时，我们需要降低特征空间维度。实现这一目标有两种方法，一是使用池化层，二是使用Stride（步幅）
-
滑动卷积核时，我们会先从输入的左上角开始，每次往左滑动一列或者往下滑动一行逐一计算输出，我们将每次滑动的行数和列数称为Stride。
-
Stride的作用是成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3。以此类推。
填充：
-
填充（padding）:未来保留输入边界特征，一般时0值填充
-
边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外,所以输入图像的边缘被“修剪”掉了。这是不理想的，通常我们都希望输入和输出的大小应该保持一致。
-
Padding就是针对这个问题提出的一个解决方案：它会用额外的“假”像素填充边缘（值一般为0），这样，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入大小相同。
感受野：
-
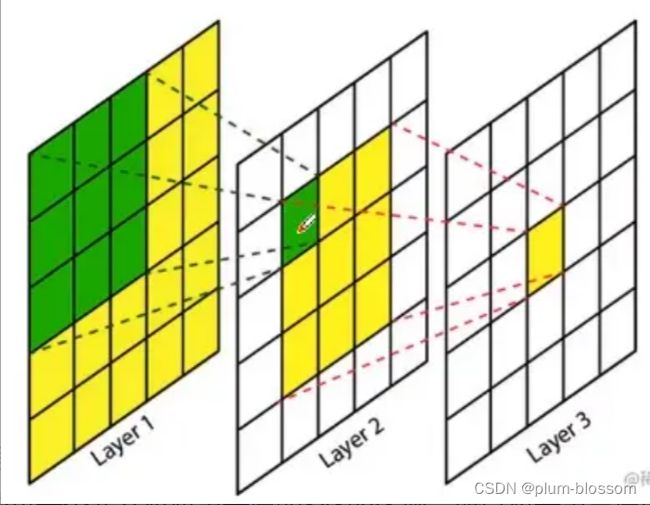
感受野（Receptive Field），指的是神经网络中神经元“看到的”输入区域，再卷积神经网络中，feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。
-
对于第二层，在上一层对应到的是3x3的区域，这个3x3的区域就是一个感受野；第三层的每一个元素对应第二层的3x3的区域，第二层的每一个元素对应第一层的3x3的区域，所以对于第三层而言，对应第二层的3x3的区域，对应第一层的5x5的区域，经过三层卷积之后，第三层对应原图的感受野是5x5的。
-
用小的卷积核来代替大的卷积核，可以加深网络，可以增大网络的非线性表达能力，因为可以对每一层加一个relu来进行激活，引入非线性的变化因素。
二、探究不同卷积核的作用
-
大卷积核
- 优点：感受域范围大
- 举例：AlexNet、LeNet等网络都使用了比较大的卷积核，如5×5、11×11
- 缺点：参数量多：计算量大
-
小卷积核
- 优点：参数量少；计算量小；整合三个非线性激活层代替单一非线性激活层，增加模型判别能力
- 举例：VGG之后
- 缺点：感受域不足；深度堆叠卷积（也就是堆叠非线性激活），容易出现不可控的因素
-
1×1卷积
- 增加非线性： 1×1卷积核的卷积过程相当于全连接层的计算过程，并且还加入了非线性激活函数，从而可以增加网络的非线性，使得网络可以表达更加复杂的特征。
-
空洞卷积：
- 标准的3×3卷积核只能看到对应区域3×3的大小，但是为了能让卷积核看到更大的范围，dilated conv使其成为了可能。pooling下采样操作导致的信息丢失是不可逆的，这不利于像素级任务，用空洞卷积代替pooling的作用（成倍的增加感受野）更适用于语义分割。
-
非对称卷积
- 将标准3×3卷积分成一个1×3卷积和3×1卷积，在不改变感受野大小的情况下可减少计算量。标准卷积计算量：9×9 = 81次乘法，非对称卷积计算量：3×15+3×9 = 72次乘法。注意：非对称卷积用在分辨率为12-20大小的特征图上效果会比较好
三、编程实现
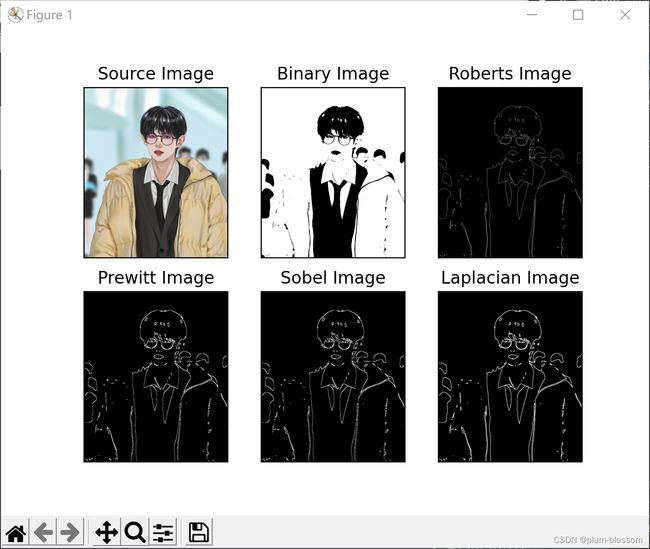
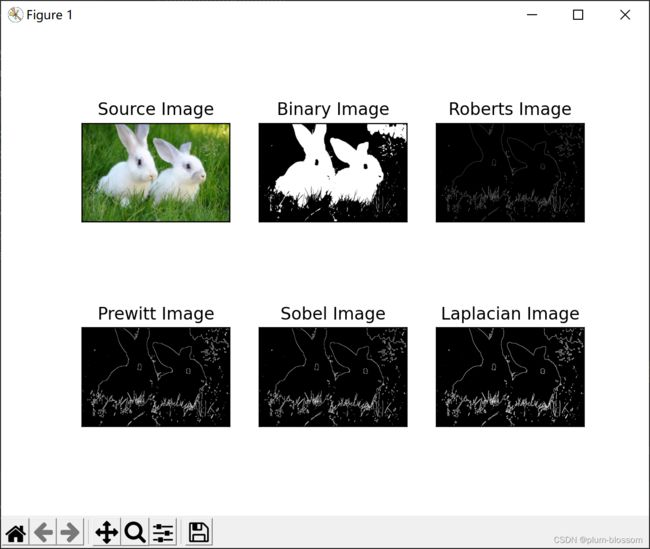
1.实现灰度图的边缘检测、锐化、模糊。（必做）
#encoding:utf-8
#By:Eastmount CSDN 2021-07-19
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图像
img = cv2.imread('./13.jpg')
lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
#灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#高斯滤波
gaussianBlur = cv2.GaussianBlur(grayImage, (3,3), 0)
#阈值处理
ret, binary = cv2.threshold(gaussianBlur, 127, 255, cv2.THRESH_BINARY)
#Roberts算子
kernelx = np.array([[-1,0],[0,1]], dtype=int)
kernely = np.array([[0,-1],[1,0]], dtype=int)
x = cv2.filter2D(binary, cv2.CV_16S, kernelx)
y = cv2.filter2D(binary, cv2.CV_16S, kernely)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
#Prewitt算子
kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]], dtype=int)
kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]], dtype=int)
x = cv2.filter2D(binary, cv2.CV_16S, kernelx)
y = cv2.filter2D(binary, cv2.CV_16S, kernely)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Prewitt = cv2.addWeighted(absX,0.5,absY,0.5,0)
#Sobel算子
x = cv2.Sobel(binary, cv2.CV_16S, 1, 0)
y = cv2.Sobel(binary, cv2.CV_16S, 0, 1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
#拉普拉斯算法
dst = cv2.Laplacian(binary, cv2.CV_16S, ksize = 3)
Laplacian = cv2.convertScaleAbs(dst)
#效果图
titles = ['Source Image', 'Binary Image', 'Roberts Image',
'Prewitt Image','Sobel Image', 'Laplacian Image']
images = [lenna_img, binary, Roberts, Prewitt, Sobel, Laplacian]
for i in np.arange(6):
plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
读入一个灰度图：
边缘检测：
锐化：
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图像
img = cv2.imread('./13.jpg')
lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
#灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#高斯滤波
gaussianBlur = cv2.GaussianBlur(grayImage, (3,3), 0)
#阈值处理
ret, binary = cv2.threshold(gaussianBlur, 127, 255, cv2.THRESH_BINARY)
#Roberts算子
kernelx = np.array([[-1,0],[0,1]], dtype=int)
kernely = np.array([[0,-1],[1,0]], dtype=int)
x = cv2.filter2D(binary, cv2.CV_16S, kernelx)
y = cv2.filter2D(binary, cv2.CV_16S, kernely)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
#Prewitt算子
kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]], dtype=int)
kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]], dtype=int)
x = cv2.filter2D(binary, cv2.CV_16S, kernelx)
y = cv2.filter2D(binary, cv2.CV_16S, kernely)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Prewitt = cv2.addWeighted(absX,0.5,absY,0.5,0)
#Sobel算子
x = cv2.Sobel(binary, cv2.CV_16S, 1, 0)
y = cv2.Sobel(binary, cv2.CV_16S, 0, 1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
#拉普拉斯算法
dst = cv2.Laplacian(binary, cv2.CV_16S, ksize = 3)
Laplacian = cv2.convertScaleAbs(dst)
#效果图
titles = ['Source Image', 'Binary Image', 'Roberts Image',
'Prewitt Image','Sobel Image', 'Laplacian Image']
images = [lenna_img, binary, Roberts, Prewitt, Sobel, Laplacian]
for i in np.arange(6):
plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
模糊：
①均值模糊：
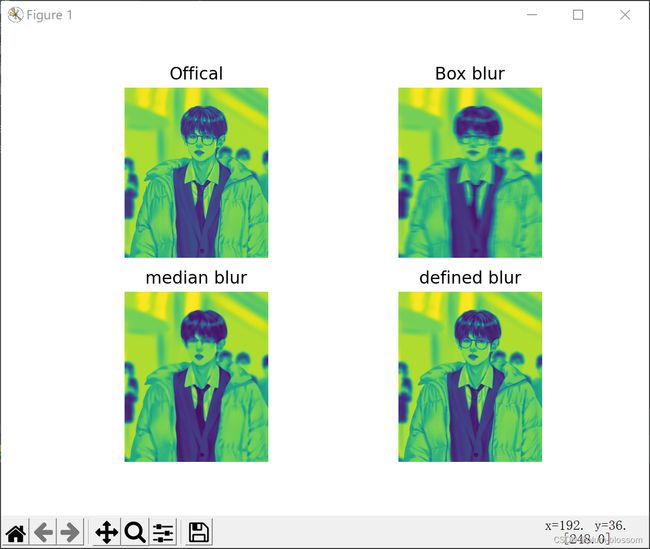
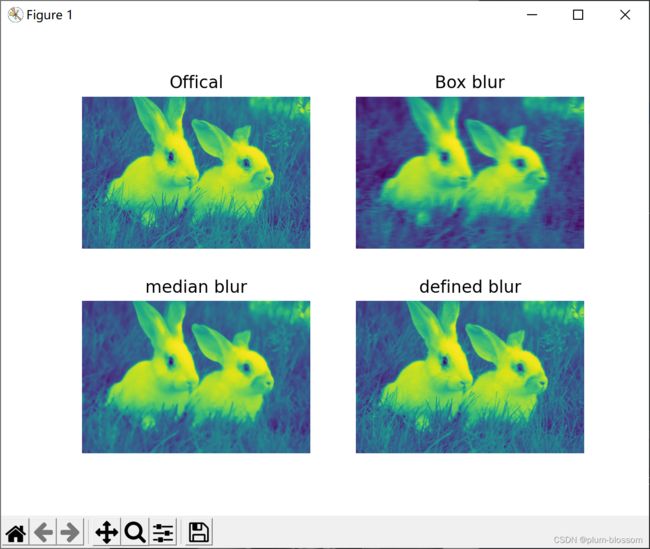
# 图像模糊处理
# 均值模糊 box blur
import cv2
import numpy as np
import matplotlib.pyplot as plt
if __name__ == "__main__":
image = cv2.imread('./13.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 此为均值模糊
# （30,1）为一维卷积核，指在x，y方向偏移多少位
dst1 = cv2.blur(image, (30, 1))
# 此为中值模糊，常用于去除椒盐噪声
dst2 = cv2.medianBlur(image, 15)
# 自定义卷积核，执行模糊操作，也可定义执行锐化操作
kernel = np.ones([5, 5], np.float32) / 25
dst3 = cv2.filter2D(image, -1, kernel=kernel)
plt.subplot(2, 2, 1)
plt.imshow(image)
plt.axis('off')
plt.title('Offical')
plt.subplot(2, 2, 2)
plt.imshow(dst1)
plt.axis('off')
plt.title('Box blur')
plt.subplot(2, 2, 3)
plt.imshow(dst2)
plt.axis('off')
plt.title('median blur')
plt.subplot(2, 2, 4)
plt.imshow(dst3)
plt.axis('off')
plt.title('defined blur')
plt.show()
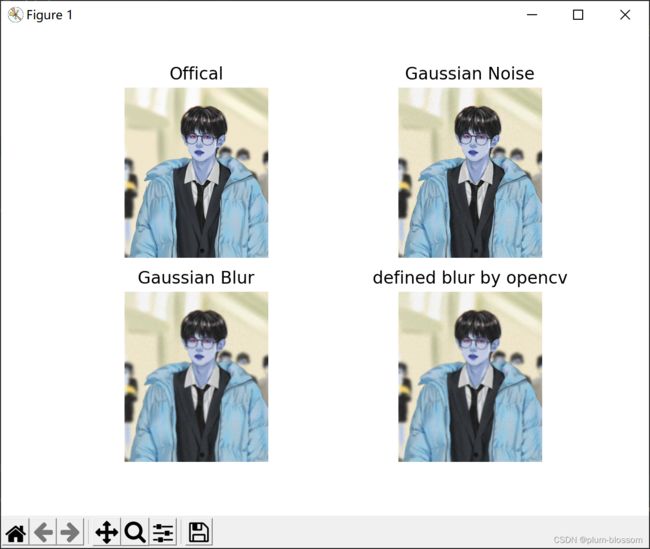
②高斯模糊：
# 图像模糊处理
# 高斯模糊 gaussian blur
# 使用自编写高斯噪声及自编写高斯模糊函数与自带高斯函数作效果对比
import cv2
import numpy as np
import matplotlib.pyplot as plt
def clamp(pv):
if pv > 255:
return 255
if pv < 0:
return 0
else:
return pv
def gaussian_noise(image): # 加高斯噪声
h, w, c = image.shape
for row in range(h):
for col in range(w):
s = np.random.normal(0, 20, 3)
b = image[row, col, 0] # blue
g = image[row, col, 1] # green
r = image[row, col, 2] # red
image[row, col, 0] = clamp(b + s[0])
image[row, col, 1] = clamp(g + s[1])
image[row, col, 2] = clamp(r + s[2])
dst = cv2.GaussianBlur(image, (15, 15), 0) # 高斯模糊
return dst, image
if __name__ == "__main__":
src = cv2.imread('./13.jpg')
plt.subplot(2, 2, 1)
plt.imshow(src)
plt.axis('off')
plt.title('Offical')
output, noise = gaussian_noise(src)
cvdst = cv2.GaussianBlur(src, (15, 15), 0) # 高斯模糊
plt.subplot(2, 2, 2)
plt.imshow(noise)
plt.axis('off')
plt.title('Gaussian Noise')
plt.subplot(2, 2, 3)
plt.imshow(output)
plt.axis('off')
plt.title('Gaussian Blur')
plt.subplot(2, 2, 4)
plt.imshow(cvdst)
plt.axis('off')
plt.title('defined blur by opencv')
plt.show()
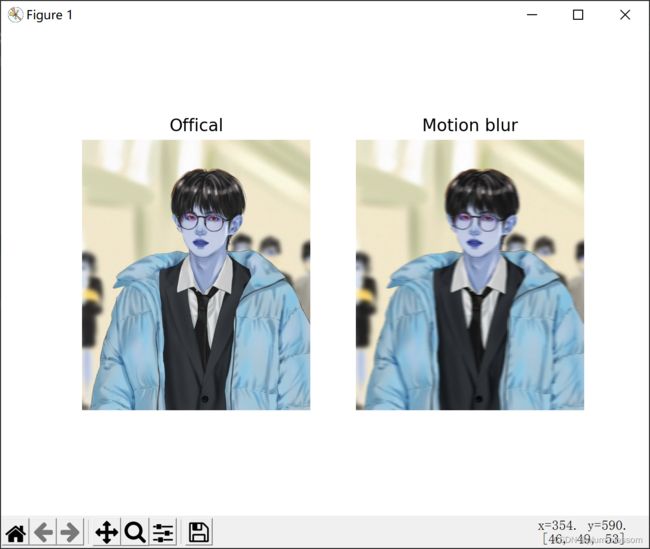
③运动模糊：
# 图像模糊处理
# 运动模糊，亦称动态模糊，motion blur
# 运动模糊：由于相机和物体之间的相对运动造成的模糊
import numpy as np
import cv2
import matplotlib.pyplot as plt
def motion_blur(image, degree=12, angle=45):
image = np.array(image)
# 这里生成任意角度的运动模糊kernel的矩阵， degree越大，模糊程度越高
M = cv2.getRotationMatrix2D((degree / 2, degree / 2), angle, 1)
motion_blur_kernel = np.diag(np.ones(degree))
motion_blur_kernel = cv2.warpAffine(motion_blur_kernel, M, (degree, degree))
motion_blur_kernel = motion_blur_kernel / degree
blurred = cv2.filter2D(image, -1, motion_blur_kernel)
# convert to uint8
cv2.normalize(blurred, blurred, 0, 255, cv2.NORM_MINMAX)
blurred = np.array(blurred, dtype=np.uint8)
return blurred
if __name__ == "__main__":
img = cv2.imread('./13.jpg')
dst = motion_blur(img)
plt.subplot(1, 2, 1)
plt.imshow(img)
plt.axis('off')
plt.title('Offical')
plt.subplot(1, 2, 2)
plt.imshow(dst)
plt.axis('off')
plt.title('Motion blur')
plt.show()
2.调整卷积核参数，测试并总结。（必做）
调整卷积核参数，设置padding为2
padding=10
stride=2：
stride=3：
stride=5：
步长：保留相邻区域特征的相关性。步长小，提取的特征会更全面。步长大，计算量会下降，但是可能错漏关键信息。
3.使用不同尺寸图片，测试并总结。（必做）
原图：
边缘检测：
锐化：
模糊（均值模糊）：
4.探索更多类型卷积核。（选做）
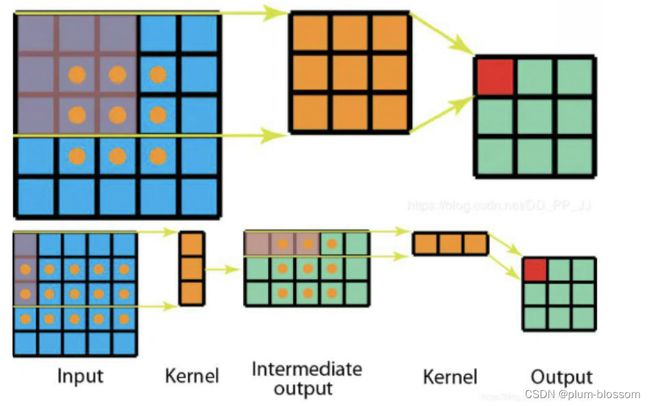
- 转置卷积（反卷积）：在现代CNN网络中非常常用，主要是因为它们具有增加图像尺寸的能力。
- 可分离卷积
- 可分离卷积是指将卷积kernel分解为低维kernel。可分离卷积有两种主要类型。使用可分离卷积可以显著减少所需参数的数量。
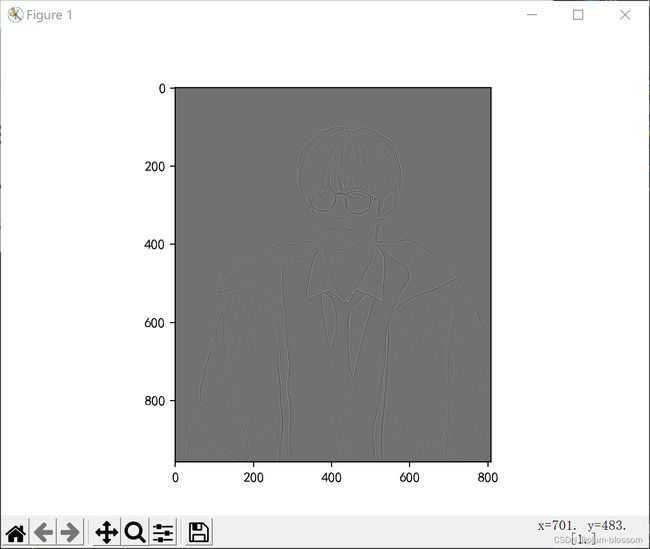
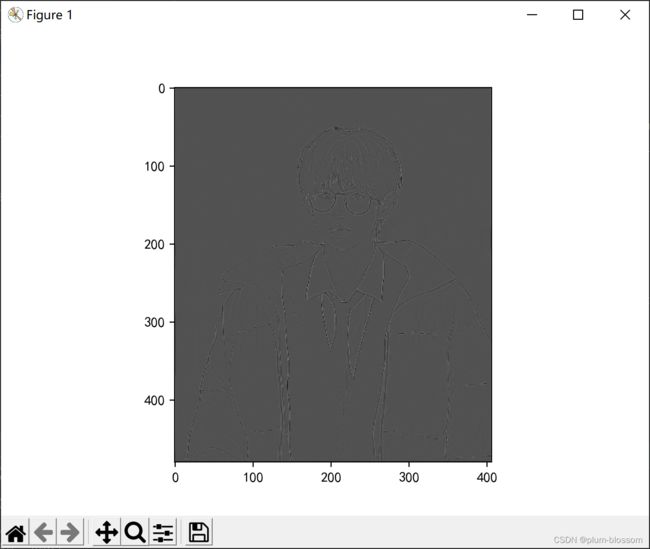
5.尝试彩色图片边缘检测。（选做）
将彩色图片转换为灰度图进行边缘检测：
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
im = Image.open(r'./12.jpg').convert('L') # 读入一张灰度图的图片
im = np.array(im, dtype='float32') # 将其转换为一个矩阵
#print(im.shape[0],im.shape[1]) 448*448
# 可视化图片
plt.imshow(im.astype('uint8'), cmap='gray')
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
conv1 = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=3, bias=False,stride=1,padding=1) # 定义卷积
sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32') # 定义轮廓检测算子
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3)) # 适配卷积的输入输出
conv1.weight.data = torch.from_numpy(sobel_kernel) # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im)) # 作用在图片上
edge1 = edge1.data.squeeze().numpy() # 将输出转换为图片的格式
plt.imshow(edge1, cmap='gray')
plt.show()
原图：
边缘检测：
总结
本次作业的心得体会，重点谈谈卷积能够提取特征的原理。
本次实验回顾了卷积、卷积核、特征图、特征选择、步长、填充、感受野的概念，conv2d函数的使用，深入探究了不同卷积核的作用，并且编程实现了灰度图的边缘检测，锐化，模糊等。
卷积能够提取特征的原理：从信号与系统的角度看，卷积很多时候出现在一个系统的单位脉冲响应与输入信号上，用于求出系统在一定输入下所对应的输出。
神经网络的多层结构从一开始的设想是模仿生物的神经元的一层一层传递的结构，从一开始的神经元判断角和边等等到大的局部特征最终得到所看到的目标是否是与神经元中记忆的某一个模式所匹配来进行目标的判断。
在卷积神经网络中，每一个卷积核所对应的卷积层实际上就是一个用于判断图像中某一个特征的系统。但是我们对这个系统的具体运算法则并不清楚，所以我们需要通过误差反向传播的方式，不断地调整卷积核中的参数，使得在训练后卷积核能够能够完成判断某一个图像特征的工作。当所有的单个卷积层（单个特征判断系统）都能有效地完成特征判断的任务时，由这些数量众多卷积层所组成的复杂系统CNN，就能够完成人类所需要的给予卷积神经网络的复杂任务。
参考
卷积核的类型及作用
6.2. 图像卷积 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
Pytorch——卷积神经网络
图像中的卷积为何能够提取特征