广州大学学生实验报告, 人工智能原理实验,实验2搜索方法与,简单易懂
广州大学学生实验报告
开课学院及实验室:计算机学院/电子信息楼 416B 2022年 10 月 20日
| 学 院 |
计算机科学与网络工程学院 |
年级/专业/班 |
计科 |
姓名 |
Great Macro |
学号 |
|
| 实验课程名称 |
人工智能原理实验 |
成绩 |
|||||
| 实验项目名称 |
实验2搜索方法 |
指导老师 |
|||||
实验二 搜索方法
- 实验目的
本实验课程是计算机、智能、物联网等专业学生的一门专业课程,通过实验,帮助学生更好地掌握人工智能相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对智能程序、智能算法等有比较深入的认识。
- 掌握人工智能中涉及的相关概念、算法。
- 熟悉人工智能中的知识表示方法;
- 熟悉盲目搜索和启发式搜索算法的应用;
- 掌握问题表示、求解及编程实现。
- 掌握不同搜索策略的设计思想、步骤、性能。
二、基本要求
- 实验前,复习《人工智能》课程中的有关内容。
- 准备好实验数据。
- 编程要独立完成,程序应加适当的注释。
- 完成实验报告。
三、实验软件
使用C或C++(Visual studio)(不限制语言使用)。
四、实验内容:
(1)
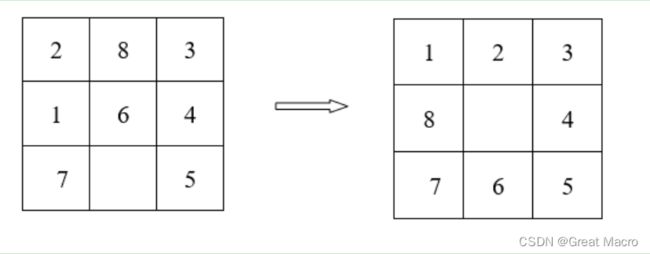
- 在图1,3*3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空。
- 如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态(图1左)到目标状态(图1右)。
- 可自行设计初始状态。目标状态为数字从小到大按顺时针排列。
- 分别用广度优先搜索策略、深度优先搜索策略和启发式搜索算法(A*算法)求解八数码问题;分析估价函数对启发式搜索算法的影响;探究各个搜索算法的特点。
BFS算法
#include#include #include #define N 3 // 阶数,可以改为更高阶 // 定义一个结构体来表示棋盘状态 typedef struct node { int data[N][N]; // 存放棋盘状态 struct node *prev; // 链表中的前指针 struct node *next; // 链表中的后指针 struct node *father;// 搜索树的父节点 }node; node *open; // open表,存放未拓展的节点 node *close; // close表,存放已经拓展的节点 static int n = 0; // 用来记录总共搜索的次数 int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5}; // 初始状态 int cur[N][N]; // 当前状态 int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; // 目标状态 // 生成一个节点 node *initList() { int i, j; node *p = malloc(sizeof(node)); if(!p) { printf("malloc fail\n"); return NULL; } p->prev = p; p->next = p; p->father = NULL; // 初始化棋盘状态 for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { p->data[i][j] = -1; } } return p; } // 头插法,把节点插入到链表头部 void head_insert(node *head, node *p) { p->next = head->next; p->prev = head; head->next->prev = p; head->next = p; } // 尾插法,把节点插入到链表尾部 void tail_insert(node *head, node *p) { p->prev = head->prev; head->prev->next = p; p->next = head; head->prev = p; } // 弹出节点 void Remove(node *p) { p->prev->next = p->next; p->next->prev = p->prev; p->next = p; p->prev = p; } // 清空链表 void clearList(node *head) { // 空表不需要再清空 if(!head || head->next == head) { printf("list is null\n"); return; } // 头删法,跟头插法相似,循环删除首元节点 for(node *p = head->next; p != head; p = head->next) { Remove(p); // 弹出节点p free(p); // 释放节点p的空间 } } // 初始化棋盘 void init() { int i, j, k; int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; int flag[N*N] = {0}; // 用来标记0~8中哪个数字已经出现过 srand(time(0)); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 尝试生成一个0~8间的数字 k = rand()%(N*N); while(1) { // 如果该数字未出现 if(flag[k] == 0) { flag[k] = 1; // 修改标志位 src[i][j] = a[k]; // 初始化对应src的位置 break; } // 重新生成数字 k = rand()%(N*N); } } } } // 复制棋盘状态 void copy(int source[N][N], int dest1[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { dest1[i][j] = source[i][j]; } } } // 打印棋盘状态 void display(int s[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 把0当做空格输出 if(s[i][j] > 0) { printf("%d ", s[i][j]); } else if(s[i][j] == 0) { printf(" "); } } printf("\n"); } } // 寻找出棋盘中的空格键 void findSpace(int s[N][N], int *x, int *y) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(s[i][j] == 0) // 找到空格 { *x = i; *y = j; } } } } // 空格上移 void up(int s[N][N], int x, int y) { // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { s[x][y] = s[x-1][y]; s[x-1][y] = 0; } } // 空格下移 void down(int s[N][N], int x, int y) { // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { s[x][y] = s[x+1][y]; s[x+1][y] = 0; } } // 空格左移 void left(int s[N][N], int x, int y) { // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { s[x][y] = s[x][y-1]; s[x][y-1] = 0; } } // 空格右移 void right(int s[N][N], int x, int y) { // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { s[x][y] = s[x][y+1]; s[x][y+1] = 0; } } // 检查close表中是否有重复的状态 int checkSame(int cmp[N][N]) { int i, j; node *p; for(p = close->next; p != close; p = p->next) { for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(p->data[i][j] != cmp[i][j]) { i = N + 1; break; } } } if(i == N && j == N) { return 1; } } return 0; } // 检查当前棋盘状态是否为目标状态 int checkWin() { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 检测到有不同的就立马返回,节省时间 if(cur[i][j] != dest[i][j]) { return 0; } } } return 1; } // 打印从初始状态到目标状态的路径 void showWin() { int i = 1; node *p, *win; // 创建一个win表,用来存放路径 win = initList(); if(!win) { printf("win malloc fail\n"); return; } // 由于节点中只有father(父节点),而打印路径是从父节点开始的 // 所以必须先从close表选择出正确的路径,因为close中可能存放不是正确路径的节点 // 可以唯一确定的是 close->prev 一定是目的状态,由此循环往上寻找其父节点 for(p = close->prev; p && p != close; p = p->father) { Remove(p); // 从close表中弹出p节点 head_insert(win, p); // 把p节点用头插法插入到win表中 } printf("the solution as follow:\n"); // 经过头插法创建的win表,一定是按从初始状态到目标状态的排序的 for(p = win->next; p != win; p = p->next, i++) { printf("step %d:\n", i); display(p->data); printf("\n"); } clearList(win); // 清空win表 free(win); // 回收内存 } // 把当前节点(tmp) 的后继节点插入到open表中 void add(node *tmp, int cmp[N][N]) { node *p = initList(); if(!p) { printf("malloc fail\n"); return; } copy(cmp, p->data); // 复制棋盘状态 p->father = tmp; // 修改父节点指针 tail_insert(open, p); // BFS用尾插法,DFS用头插法 } // 广度优先搜索法 void BFS() { printf("start BFS\n"); node *tmp; int x, y, k, cmp[N][N]; add(NULL, src); // 把初始状态加入到open表中 while(1) { // 如果open表为空,就可以退出了 if(open->next == open) { printf("fail\n"); return ; } // 从open表中取出首元节点,插入到close表的末尾 tmp = open->next; Remove(tmp); tail_insert(close, tmp); printf("now go :%d\n", ++n); // 打印当前搜索出的棋盘状态 copy(tmp->data, cur); printf("current:\n"); display(cur); // 检测当前棋盘状态是否为目标状态 if(checkWin()) { printf("success\n\n"); showWin(); return; } k = 0; // 记录当前节点的后继节点个数 findSpace(cur, &x, &y); // 寻找当前棋盘状态的空格坐标 printf("try up\n"); // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 up(cmp, x, y); // cmp尝试向上移 // 判断cmp上移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can up\n"); } } printf("try down\n"); // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 down(cmp, x, y); // cmp尝试向下移 // 判断cmp下移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can down\n"); } } printf("try left\n"); // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 left(cmp, x, y); // cmp尝试向左移 // 判断cmp左移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can left\n"); } } printf("try right\n"); // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 right(cmp, x, y); // cmp尝试向右移 // 判断cmp右移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can right\n"); } } // 如果当前状态没有后继节点,应该从close表中删除该状态 if(k == 0) { Remove(tmp); // 弹出当前状态 free(tmp); // 释放当前状态 printf("del done\n\n"); } } } int main() { open = initList(); // 初始化open表 close = initList(); // 初始化close表 if(!open || !close) { printf("初始化状态失败\n"); return -1; } // 测试阶段建议直接定义src, init()后的src很大程度上无解 // init(); printf("src:\n"); display(src); BFS(); // 清空open表和close表并回收内存 clearList(open); clearList(close); free(open); free(close); printf("BFS finish\n"); return 0; }
DFS算法
#include#include #include #define N 3 // 阶数,可以改为更高阶 // 定义一个结构体来表示棋盘状态 typedef struct node { int data[N][N]; // 存放棋盘状态 struct node *prev; // 链表中的前指针 struct node *next; // 链表中的后指针 struct node *father;// 搜索树的父节点 }node; node *open; // open表,存放未拓展的节点 node *close; // close表,存放已经拓展的节点 static int n = 0; // 用来记录总共搜索的次数 int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5}; // 初始状态 int cur[N][N]; // 当前状态 int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; // 目标状态 // 生成一个节点 node *initList() { int i, j; node *p = malloc(sizeof(node)); if(!p) { printf("malloc fail\n"); return NULL; } p->prev = p; p->next = p; p->father = NULL; // 初始化棋盘状态 for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { p->data[i][j] = -1; } } return p; } // 头插法,把节点插入到链表头部 void head_insert(node *head, node *p) { p->next = head->next; p->prev = head; head->next->prev = p; head->next = p; } // 尾插法,把节点插入到链表尾部 void tail_insert(node *head, node *p) { p->prev = head->prev; head->prev->next = p; p->next = head; head->prev = p; } // 弹出节点 void Remove(node *p) { p->prev->next = p->next; p->next->prev = p->prev; p->next = p; p->prev = p; } // 清空链表 void clearList(node *head) { // 空表不需要再清空 if(!head || head->next == head) { printf("list is null\n"); return; } // 头删法,跟头插法相似,循环删除首元节点 for(node *p = head->next; p != head; p = head->next) { Remove(p); // 弹出节点p free(p); // 释放节点p的空间 } } // 初始化棋盘 void init() { int i, j, k; int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; int flag[N*N] = {0}; // 用来标记0~8中哪个数字已经出现过 srand(time(0)); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 尝试生成一个0~8间的数字 k = rand()%(N*N); while(1) { // 如果该数字未出现 if(flag[k] == 0) { flag[k] = 1; // 修改标志位 src[i][j] = a[k]; // 初始化对应src的位置 break; } // 重新生成数字 k = rand()%(N*N); } } } } // 复制棋盘状态 void copy(int source[N][N], int dest1[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { dest1[i][j] = source[i][j]; } } } // 打印棋盘状态 void display(int s[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 把0当做空格输出 if(s[i][j] > 0) { printf("%d ", s[i][j]); } else if(s[i][j] == 0) { printf(" "); } } printf("\n"); } } // 寻找出棋盘中的空格键 void findSpace(int s[N][N], int *x, int *y) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(s[i][j] == 0) // 找到空格 { *x = i; *y = j; } } } } // 空格上移 void up(int s[N][N], int x, int y) { // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { s[x][y] = s[x-1][y]; s[x-1][y] = 0; } } // 空格下移 void down(int s[N][N], int x, int y) { // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { s[x][y] = s[x+1][y]; s[x+1][y] = 0; } } // 空格左移 void left(int s[N][N], int x, int y) { // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { s[x][y] = s[x][y-1]; s[x][y-1] = 0; } } // 空格右移 void right(int s[N][N], int x, int y) { // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { s[x][y] = s[x][y+1]; s[x][y+1] = 0; } } // 检查close表中是否有重复的状态 int checkSame(int cmp[N][N]) { int i, j; node *p; for(p = close->next; p != close; p = p->next) { for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(p->data[i][j] != cmp[i][j]) { i = N + 1; break; } } } if(i == N && j == N) { return 1; } } return 0; } // 检查当前棋盘状态是否为目标状态 int checkWin() { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 检测到有不同的就立马返回,节省时间 if(cur[i][j] != dest[i][j]) { return 0; } } } return 1; } // 打印从初始状态到目标状态的路径 void showWin() { int i = 1; node *p, *win; // 创建一个win表,用来存放路径 win = initList(); if(!win) { printf("win malloc fail\n"); return; } // 由于节点中只有father(父节点),而打印路径是从父节点开始的 // 所以必须先从close表选择出正确的路径,因为close中可能存放不是正确路径的节点 // 可以唯一确定的是 close->prev 一定是目的状态,由此循环往上寻找其父节点 for(p = close->prev; p && p != close; p = p->father) { Remove(p); // 从close表中弹出p节点 head_insert(win, p); // 把p节点用头插法插入到win表中 } printf("the solution as follow:\n"); // 经过头插法创建的win表,一定是按从初始状态到目标状态的排序的 for(p = win->next; p != win; p = p->next, i++) { printf("step %d:\n", i); display(p->data); printf("\n"); } clearList(win); // 清空win表 free(win); // 回收内存 } // 把当前节点(tmp) 的后继节点插入到open表中 void add(node *tmp, int cmp[N][N]) { node *p = initList(); if(!p) { printf("malloc fail\n"); return; } copy(cmp, p->data); // 复制棋盘状态 p->father = tmp; // 修改父节点指针 head_insert(open, p); // BFS用尾插法,DFS用头插法 } // 深度优先搜索法 void DFS() { printf("start BFS\n"); node *tmp; int x, y, k, cmp[N][N]; add(NULL, src); // 把初始状态加入到open表中 while(1) { // 如果open表为空,就可以退出了 if(open->next == open) { printf("fail\n"); return ; } // 从open表中取出首元节点,插入到close表的末尾 tmp = open->next; Remove(tmp); tail_insert(close, tmp); printf("now go :%d\n", ++n); // 打印当前搜索出的棋盘状态 copy(tmp->data, cur); printf("current:\n"); display(cur); // 检测当前棋盘状态是否为目标状态 if(checkWin()) { printf("success\n\n"); printf("solution as follow:\n"); showWin(); return; } k = 0; // 记录当前节点的后继节点个数 findSpace(cur, &x, &y); // 寻找当前棋盘状态的空格坐标 printf("try up\n"); // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 up(cmp, x, y); // cmp尝试向上移 // 判断cmp上移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can up\n"); } } printf("try down\n"); // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 down(cmp, x, y); // cmp尝试向下移 // 判断cmp下移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can down\n"); } } printf("try left\n"); // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 left(cmp, x, y); // cmp尝试向左移 // 判断cmp左移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can left\n"); } } printf("try right\n"); // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 right(cmp, x, y); // cmp尝试向右移 // 判断cmp右移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can right\n"); } } // 如果当前状态没有后继节点,应该从close表中删除该状态 if(k == 0) { Remove(tmp); // 弹出当前状态 free(tmp); // 释放当前状态 printf("del done\n\n"); } } } int main() { open = initList(); // 初始化open表 close = initList(); // 初始化close表 if(!open || !close) { printf("初始化状态失败\n"); return -1; } // 测试阶段建议直接定义src, init()后的src很大程度上无解 // init(); printf("src:\n"); display(src); DFS(); // 清空open表和close表并回收内存 clearList(open); clearList(close); free(open); free(close); printf("DFS finish\n"); return 0; }
UCS算法
#include#include #include #include #define N 3 // 阶数,可以改为更高阶 // 定义一个结构体来表示棋盘状态 typedef struct node { int cost; // 从初始状态到本状态的代价 int data[N][N]; // 存放棋盘状态 struct node *prev; // 链表中的前指针 struct node *next; // 链表中的后指针 struct node *father;// 搜索树的父节点 }node; node *open; // open表,存放未拓展的节点 node *close; // close表,存放已经拓展的节点 static int n = 0; // 用来记录总共搜索的次数 int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5}; // 初始状态 int cur[N][N]; // 当前状态 int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; // 目标状态 // 生成一个节点 node *initList() { int i, j; node *p = malloc(sizeof(node)); if(!p) { printf("malloc fail\n"); return NULL; } p->prev = p; p->next = p; p->father = NULL; p->cost = 0; // 初始化棋盘状态 for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { p->data[i][j] = -1; } } return p; } // 头插法,把节点插入到链表头部 void head_insert(node *head, node *p) { p->next = head->next; p->prev = head; head->next->prev = p; head->next = p; } // 尾插法,把节点插入到链表尾部 void tail_insert(node *head, node *p) { p->prev = head->prev; head->prev->next = p; p->next = head; head->prev = p; } // 弹出节点 void Remove(node *p) { p->prev->next = p->next; p->next->prev = p->prev; p->next = p; p->prev = p; } // 清空链表 void clearList(node *head) { // 空表不需要再清空 if(!head || head->next == head) { printf("list is null\n"); return; } // 头删法,跟头插法相似,循环删除首元节点 for(node *p = head->next; p != head; p = head->next) { Remove(p); // 弹出节点p free(p); // 释放节点p的空间 } } // 初始化棋盘 void init() { int i, j, k; int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; int flag[N*N] = {0}; // 用来标记0~8中哪个数字已经出现过 srand(time(0)); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 尝试生成一个0~8间的数字 k = rand()%(N*N); while(1) { // 如果该数字未出现 if(flag[k] == 0) { flag[k] = 1; // 修改标志位 src[i][j] = a[k]; // 初始化对应src的位置 break; } // 重新生成数字 k = rand()%(N*N); } } } } // 复制棋盘状态 void copy(int source[N][N], int dest1[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { dest1[i][j] = source[i][j]; } } } // 打印棋盘状态 void display(int s[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 把0当做空格输出 if(s[i][j] > 0) { printf("%d ", s[i][j]); } else if(s[i][j] == 0) { printf(" "); } } printf("\n"); } } // 寻找出棋盘中的空格键 void findSpace(int s[N][N], int *x, int *y) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(s[i][j] == 0) // 找到空格 { *x = i; *y = j; } } } } // 空格上移 void up(int s[N][N], int x, int y) { // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { s[x][y] = s[x-1][y]; s[x-1][y] = 0; } } // 空格下移 void down(int s[N][N], int x, int y) { // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { s[x][y] = s[x+1][y]; s[x+1][y] = 0; } } // 空格左移 void left(int s[N][N], int x, int y) { // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { s[x][y] = s[x][y-1]; s[x][y-1] = 0; } } // 空格右移 void right(int s[N][N], int x, int y) { // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { s[x][y] = s[x][y+1]; s[x][y+1] = 0; } } // 采用曼哈顿距离,计算从初始状态到本状态的代价 // 曼哈顿距离指,与目标位置的水平距离和垂直距离之和 // 书上给出的代价是从起始节点S到任一节点i的路径代价g(i) // 修改代价时,采用g(j) = g(i) + cost(i, j); // cost(i, j)指从当前i节点到它的后继节点j的代价 // 但是这里因为每次空格操作,只会改变2个位置 // 所以cost(i, j)都相同,因此可以省略,直接计算g(j) void compute_cost(node *p) { int i, j, m, n; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 如果有对应位置不匹配的 // 则重头搜索出与src[i][j]匹配的p->data[m][n] if(p->data[i][j] != src[i][j]) { for(m = 0; m < N; m++) { for(n = 0; n < N; n++) { // 搜索到与src[i][j]匹配的p->data[m][n] // 计算曼哈顿距离后立马结束搜索 if(p->data[m][n] == src[i][j]) { // 累加每个位置的曼哈顿距离 p->cost += abs(m-i) + abs(n-j); m = N; // 修改m值,结束搜索 break; } } } } } } } // 检查close表中是否有重复的状态 int checkSame(int cmp[N][N]) { int i, j; node *p; for(p = close->next; p != close; p = p->next) { for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(p->data[i][j] != cmp[i][j]) { i = N + 1; break; } } } if(i == N && j == N) { return 1; } } return 0; } // 检查当前棋盘状态是否为目标状态 int checkWin() { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 检测到有不同的就立马返回,节省时间 if(cur[i][j] != dest[i][j]) { return 0; } } } return 1; } // 打印从初始状态到目标状态的路径 void showWin() { int i = 1; node *p, *win; // 创建一个win表,用来存放路径 win = initList(); if(!win) { printf("win malloc fail\n"); return; } // 由于节点中只有father(父节点),而打印路径是从父节点开始的 // 所以必须先从close表选择出正确的路径,因为close中可能存放不是正确路径的节点 // 可以唯一确定的是 close->prev 一定是目的状态,由此循环往上寻找其父节点 for(p = close->prev; p && p != close; p = p->father) { Remove(p); // 从close表中弹出p节点 head_insert(win, p); // 把p节点用头插法插入到win表中 } printf("the solution as follow:\n"); // 经过头插法创建的win表,一定是按从初始状态到目标状态的排序的 for(p = win->next; p != win; p = p->next, i++) { printf("step %d:\n", i); display(p->data); printf("\n"); } clearList(win); // 清空win表 free(win); // 内存回收 } // 把当前节点(tmp) 的后继节点插入到open表中 void add(node *tmp, int cmp[N][N]) { node *p = initList(); if(!p) { printf("malloc fail\n"); return; } copy(cmp, p->data); // 复制棋盘状态 p->father = tmp; // 修改父节点指针 compute_cost(p); // 修改从初始状态到本状态的代价 head_insert(open, p); // BFS用尾插法,DFS用头插法 } // 从表中选择一个节点,使其代价p->cost最小 // 通常是从open表中选择,如果有多个点,则随便选一个 node *min_cost(node *head) { // 空表直接退出 if(!head || head->next == head) { return NULL; } node *p, *min; min = head->next; for(p = min->next; p != head; p = p->next) { // 遇到更小的,就更新min if(p->cost < min->cost) { min = p; } } return min; } // 等代价搜索法 void UCS() { printf("start UCS\n"); node *tmp; int x, y, k, cmp[N][N]; add(NULL, src); // 把初始状态加入到open表中 while(1) { // 如果open表为空,就可以退出了 if(open->next == open) { printf("fail\n"); return; } // 从open表中选择一个节点,使其代价p->cost最小 tmp = min_cost(open); // 如果tmp为空,则说明open表为空 // 但是一般不会出现,因为前面已经对open表进行判空处理 // 这里写的原因就是特意为了增强算法的健壮性 if(!tmp) { printf("fail\n"); return; } Remove(tmp); tail_insert(close, tmp); printf("now go :%d\n", ++n); // 打印当前搜索出的棋盘状态 copy(tmp->data, cur); printf("current:\n"); display(cur); // 检测当前棋盘状态是否为目标状态 if(checkWin()) { printf("success\n\n"); printf("solution as follow:\n"); showWin(); return; } k = 0; // 记录当前节点的后继节点个数 findSpace(cur, &x, &y); // 寻找当前棋盘状态的空格坐标 printf("try up\n"); // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 up(cmp, x, y); // cmp尝试向上移 // 判断cmp上移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can up\n"); } } printf("try down\n"); // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 down(cmp, x, y); // cmp尝试向下移 // 判断cmp下移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can down\n"); } } printf("try left\n"); // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 left(cmp, x, y); // cmp尝试向左移 // 判断cmp左移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can left\n"); } } printf("try right\n"); // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 right(cmp, x, y); // cmp尝试向右移 // 判断cmp右移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can right\n"); } } // 如果当前状态没有后继节点,应该从close表中删除该状态 if(k == 0) { Remove(tmp); // 弹出当前状态 free(tmp); // 释放当前状态 printf("del done\n\n"); } } } int main() { open = initList(); // 初始化open表 close = initList(); // 初始化close表 if(!open || !close) { printf("初始化状态失败\n"); return -1; } // 测试阶段建议直接定义src, init()后的src很大程度上无解 // init(); printf("src:\n"); display(src); UCS(); // 清空open表和close表并回收内存 clearList(open); clearList(close); free(open); free(close); printf("DFS finish\n"); return 0; }
Astar算法
#include#include #include #include #define N 3 // 阶数,可以改为更高阶 // 定义一个结构体来表示棋盘状态 typedef struct node { int cost; // 从初始状态到本状态的代价 int data[N][N]; // 存放棋盘状态 struct node *prev; // 链表中的前指针 struct node *next; // 链表中的后指针 struct node *father;// 搜索树的父节点 }node; node *open; // open表,存放未拓展的节点 node *close; // close表,存放已经拓展的节点 static int n = 0; // 用来记录总共搜索的次数 int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5}; // 初始状态 int cur[N][N]; // 当前状态 int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; // 目标状态 // 生成一个节点 node *initList() { int i, j; node *p = malloc(sizeof(node)); if(!p) { printf("malloc fail\n"); return NULL; } p->prev = p; p->next = p; p->father = NULL; p->cost = 0; // 初始化棋盘状态 for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { p->data[i][j] = -1; } } return p; } // 头插法,把节点插入到链表头部 void head_insert(node *head, node *p) { p->next = head->next; p->prev = head; head->next->prev = p; head->next = p; } // 尾插法,把节点插入到链表尾部 void tail_insert(node *head, node *p) { p->prev = head->prev; head->prev->next = p; p->next = head; head->prev = p; } // 弹出节点 void Remove(node *p) { p->prev->next = p->next; p->next->prev = p->prev; p->next = p; p->prev = p; } // 清空链表 void clearList(node *head) { // 空表不需要再清空 if(!head || head->next == head) { printf("list is null\n"); return; } // 头删法,跟头插法相似,循环删除首元节点 for(node *p = head->next; p != head; p = head->next) { Remove(p); // 弹出节点p free(p); // 释放节点p的空间 } } // 初始化棋盘 void init() { int i, j, k; int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5}; int flag[N*N] = {0}; // 用来标记0~8中哪个数字已经出现过 srand(time(0)); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 尝试生成一个0~8间的数字 k = rand()%(N*N); while(1) { // 如果该数字未出现 if(flag[k] == 0) { flag[k] = 1; // 修改标志位 src[i][j] = a[k]; // 初始化对应src的位置 break; } // 重新生成数字 k = rand()%(N*N); } } } } // 复制棋盘状态 void copy(int source[N][N], int dest1[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { dest1[i][j] = source[i][j]; } } } // 打印棋盘状态 void display(int s[N][N]) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 把0当做空格输出 if(s[i][j] > 0) { printf("%d ", s[i][j]); } else if(s[i][j] == 0) { printf(" "); } } printf("\n"); } } // 寻找出棋盘中的空格键 void findSpace(int s[N][N], int *x, int *y) { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(s[i][j] == 0) // 找到空格 { *x = i; *y = j; } } } } // 空格上移 void up(int s[N][N], int x, int y) { // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { s[x][y] = s[x-1][y]; s[x-1][y] = 0; } } // 空格下移 void down(int s[N][N], int x, int y) { // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { s[x][y] = s[x+1][y]; s[x+1][y] = 0; } } // 空格左移 void left(int s[N][N], int x, int y) { // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { s[x][y] = s[x][y-1]; s[x][y-1] = 0; } } // 空格右移 void right(int s[N][N], int x, int y) { // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { s[x][y] = s[x][y+1]; s[x][y+1] = 0; } } // 采用曼哈顿距离,计算从某个状态cmp到当前状态的代价 // 曼哈顿距离指,与目标位置的水平距离和垂直距离之和 // 书上给出的代价是从起始节点S到任一节点i的路径代价g(i) // 修改代价时,采用g(j) = g(i) + cost(i, j); // cost(i, j)指从当前i节点到它的后继节点j的代价 // 但是这里因为每次空格操作,只会改变2个位置 // 所以cost(i, j)都相同,因此可以省略,直接计算g(j) void compute_cost(node *p, int cmp[N][N]) { int i, j, m, n; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 如果有对应位置不匹配的 // 则重头搜索出与cmp[i][j]匹配的p->data[m][n] if(p->data[i][j] != cmp[i][j]) { for(m = 0; m < N; m++) { for(n = 0; n < N; n++) { // 搜索到与cmp[i][j]匹配的p->data[m][n] // 计算曼哈顿距离后立马结束搜索 if(p->data[m][n] == cmp[i][j]) { // 累加每个位置的曼哈顿距离 p->cost += abs(m-i) + abs(n-j); m = N; // 修改m值,结束搜索 break; } } } } } } } // 检查close表中是否有重复的状态 int checkSame(int cmp[N][N]) { int i, j; node *p; for(p = close->next; p != close; p = p->next) { for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(p->data[i][j] != cmp[i][j]) { i = N + 1; break; } } } if(i == N && j == N) { return 1; } } return 0; } // 检查当前棋盘状态是否为目标状态 int checkWin() { int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 检测到有不同的就立马返回,节省时间 if(cur[i][j] != dest[i][j]) { return 0; } } } return 1; } // 打印从初始状态到目标状态的路径 void showWin() { int i = 1; node *p, *win; // 创建一个win表,用来存放路径 win = initList(); if(!win) { printf("win malloc fail\n"); return; } // 由于节点中只有father(父节点),而打印路径是从父节点开始的 // 所以必须先从close表选择出正确的路径,因为close中可能存放不是正确路径的节点 // 可以唯一确定的是 close->prev 一定是目的状态,由此循环往上寻找其父节点 for(p = close->prev; p && p != close; p = p->father) { Remove(p); // 从close表中弹出p节点 head_insert(win, p); // 把p节点用头插法插入到win表中 } printf("the solution as follow:\n"); // 经过头插法创建的win表,一定是按从初始状态到目标状态的排序的 for(p = win->next; p != win; p = p->next, i++) { printf("step %d:\n", i); display(p->data); printf("\n"); } clearList(win); // 清空win表 free(win); // 内存回收 } // 把当前节点(tmp) 的后继节点插入到open表中 void add(node *tmp, int cmp[N][N]) { node *p = initList(); if(!p) { printf("malloc fail\n"); return; } copy(cmp, p->data); // 复制棋盘状态 p->father = tmp; // 修改父节点指针 compute_cost(p, src); // 修改从初始状态到当前状态的代价 compute_cost(p, dest); // 修改从当前状态到目标状态的代价 head_insert(open, p); // BFS用尾插法,DFS用头插法 } // 从表中选择一个节点,使其代价p->cost最小 // 通常是从open表中选择,如果有多个点,则随便选一个 node *min_cost(node *head) { // 空表直接退出 if(!head || head->next == head) { return NULL; } node *p, *min; min = head->next; for(p = min->next; p != head; p = p->next) { if(p->cost < min->cost) { min = p; } } return min; } // 等代价搜索法 void Astar() { printf("start Astar\n"); node *tmp; int x, y, k, cmp[N][N]; add(NULL, src); // 把初始状态加入到open表中 while(1) { // 如果open表为空,就可以退出了 if(open->next == open) { printf("fail\n"); return; } // 从open表中选择一个节点,使其代价p->cost最小 tmp = min_cost(open); // 如果tmp为空,则说明open表为空 // 但是一般不会出现,因为前面已经对open表进行判空处理 // 这里写的原因就是特意为了增强算法的健壮性 if(!tmp) { printf("fail\n"); return; } Remove(tmp); tail_insert(close, tmp); printf("now go :%d\n", ++n); // 打印当前搜索出的棋盘状态 copy(tmp->data, cur); printf("current:\n"); display(cur); // 检测当前棋盘状态是否为目标状态 if(checkWin()) { printf("success\n\n"); printf("solution as follow:\n"); showWin(); return; } k = 0; // 记录当前节点的后继节点个数 findSpace(cur, &x, &y); // 寻找当前棋盘状态的空格坐标 printf("try up\n"); // 空格必须是处于第2行或者第3行,才能上移 if(x >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 up(cmp, x, y); // cmp尝试向上移 // 判断cmp上移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can up\n"); } } printf("try down\n"); // 空格必须是处于第1行或者第2行,才能下移 if(x <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 down(cmp, x, y); // cmp尝试向下移 // 判断cmp下移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can down\n"); } } printf("try left\n"); // 空格必须是处于第2列或者第3列,才能左移 if(y >= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 left(cmp, x, y); // cmp尝试向左移 // 判断cmp左移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can left\n"); } } printf("try right\n"); // 空格必须是处于第1列或者第2列,才能右移 if(y <= 1) { copy(cur, cmp); // 先复制当前状态cur到cmp中 right(cmp, x, y); // cmp尝试向右移 // 判断cmp右移后close表中是否有重复状态 // 没有重复才可以把cmp状态加入到close表中 if(checkSame(cmp) == 0) { k++; // 当前节点的后继节点数加一 add(tmp, cmp); // 把后继节点加入到open表中 printf("can right\n"); } } // 如果当前状态没有后继节点,应该从close表中删除该状态 if(k == 0) { Remove(tmp); // 弹出当前状态 free(tmp); // 释放当前状态 printf("del done\n\n"); } } } int main() { open = initList(); // 初始化open表 close = initList(); // 初始化close表 if(!open || !close) { printf("初始化状态失败\n"); return -1; } // 测试阶段建议直接定义src, init()后的src很大程度上无解 // init(); printf("src:\n"); display(src); Astar(); // 清空open表和close表并回收内存 clearList(open); clearList(close); free(open); free(close); printf("DFS finish\n"); return 0; }
(2)罗马尼亚问题
根据上图以Zerind为初始状态,Bucharest为目标状态实现搜索,分别以贪婪搜索(只考虑直线距离)和A*算法求解最短路径。 按顺序列出贪婪算法探索的扩展节点和其估价函数值,A*算法探索的扩展节点和其估计值。
贪婪算法
#include#include #define N 21 // 城市个数 #define MaxInt 32768 // 定义无穷大 // 枚举城市名,给城市名从0开始编码,相当于"#define Arad 0", enum City{Arad = 0, Bucharest, Craiova, Dobreta, Eforie, Fagaras, Giurgiu, Hirsova,Iasi, Lugoj, Mehadia, Neamt, Oradea, Pitesti, Rimnicu_Vilcea, Sibiu, Timisoara,Urziceni, Vaslui, Zerind}; int arcs[N][N] = {0}; // 定义两个城市间实际距离 // 定义两个城市间的直线距离,即最短距离,小于等于实际距离 int line[N] = {366, 0, 160, 242, 161, 176, 77, 151, 226, 244, 241, 234, 380, 10, 193, 253, 329, 80, 199, 374}; // 初始化问题状态 void init() { // 定义两个城市间的距离 { arcs[Zerind][Oradea] = 71; arcs[Zerind][Arad] = 75; arcs[Arad][Sibiu] = 140; arcs[Arad][Timisoara] = 118; arcs[Oradea][Sibiu] = 151; arcs[Timisoara][Lugoj] = 111; arcs[Lugoj][Mehadia] = 70; arcs[Mehadia][Dobreta] = 75; arcs[Dobreta][Craiova] = 120; arcs[Sibiu][Fagaras] = 99; arcs[Sibiu][Rimnicu_Vilcea] = 80; arcs[Rimnicu_Vilcea][Pitesti] = 97; arcs[Rimnicu_Vilcea][Craiova] = 146; arcs[Craiova][Pitesti] = 138; arcs[Pitesti][Bucharest] = 101; arcs[Fagaras][Bucharest] = 211; arcs[Bucharest][Giurgiu] = 90; arcs[Bucharest][Urziceni] = 85; arcs[Urziceni][Hirsova] = 98; arcs[Hirsova][Eforie] = 86; arcs[Urziceni][Vaslui] = 142; arcs[Vaslui][Iasi] = 92; arcs[Iasi][Neamt] = 87; } int i, j; // 初始化剩下城市的距离,相同两个城市间距离定义为0 for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { // 如果两个城市之间可以直达,即图中两个城市节点之间的边 if(arcs[i][j] > 0) { arcs[j][i] = arcs[i][j]; } else if(arcs[j][i] > 0) { arcs[i][j] = arcs[j][i]; } // 无法直接到达的两个城市之间的距离为-1 else if(i == j) { arcs[i][j] = 0; } else { arcs[i][j] = -1; } } } } // 根据城市编码转换成城市名 void transform(int city) { switch(city) { case Arad: printf("%s\n", "Arad"); break; case Bucharest: printf("%s\n", "Bucharest"); break; case Craiova: printf("%s\n", "Craiova"); break; case Dobreta: printf("%s\n", "Dobreta"); break; case Eforie: printf("%s\n", "Eforie"); break; case Fagaras: printf("%s\n", "Fagaras"); break; case Giurgiu: printf("%s\n", "Giurgiu"); break; case Hirsova: printf("%s\n", "Hirsova"); break; case Iasi: printf("%s\n", "Iasi"); break; case Lugoj: printf("%s\n", "Lugoj"); break; case Mehadia: printf("%s\n", "Arad"); break; case Neamt: printf("%s\n", "Neamt"); break; case Oradea: printf("%s\n", "Oradea"); break; case Pitesti: printf("%s\n", "Pitesti"); break; case Rimnicu_Vilcea: printf("%s\n", "Rimnicu Vilcea"); break; case Sibiu: printf("%s\n", "Sibiu"); break; case Timisoara: printf("%s\n", "Timisoara"); break; case Urziceni: printf("%s\n", "Urziceni"); break; case Vaslui: printf("%s\n", "Vaslui"); break; case Zerind: printf("%s\n", "Zerind"); break; } } // 打印解的路径 void show(int *Path) { int i; printf("解的路径如下\n"); for(i = 0; Path[i] != -1; i++) { transform(Path[i]); // 打印当前节点 } } // 贪婪算法 void Greedy(int V0, int VN) { printf("start Greedy\n"); int i, v, w, min, cost; int S[N]; // 记录从源点V0到终点Vi是否已被确定为最短路径长度 int Path[N]; // 记录从源点V0到终点Vi的当前最短路径长度上Vi的直接前驱节点号 // 初始化解的路径,-1表示为节点没在路径,n表示n对应的城市在路径中 for(i = 0; i < N; i++) { S[i] = 0; Path[i] = -1; } cost = 0; S[V0] = 1; // 标记初始节点已经加入解的路径中 Path[0] = V0; // 把初始节点加入解的路径中 // 最多需要搜索N次,如果都没有找到,就直接结束,一般这种情况不会发生 for(i = 1; i < N; i++) { v = V0; min = MaxInt; // 从剩下的未标记的,是当前的节点的后继节点中的节点中 // 选出一个离目标的节点的距离最小的,作为下次拓展的节点 for(w = 0; w < N; w++) { if(!S[w] && arcs[Path[i-1]][w] > 0 && line[w] < min) { v = w; min = line[w]; } } S[v] = 1; // 标记已经选出的最小的节点 Path[i] = v; // 把选出的节点加入到解的路径中 cost += arcs[Path[i-1]][v]; // 累加实际代价 printf("本次拓展节点:"); transform(v); printf("估价函数值:%d\n", line[v]); // 如果选出的节点就是目标节点,结束 if(Path[i] == VN) { printf("Greedy finsih\n\n"); show(Path); printf("实际的总代价:%d\n", cost); break; } } } int main(void) { init(); Greedy(Zerind, Bucharest); return 0; }
Astar算法
#include#include #define N 21 // 城市个数 #define MaxInt 32768 // 定义无穷大 // 枚举城市名,给城市名从0开始编码,相当于"#define Arad 0", enum City{Arad = 0, Bucharest, Craiova, Dobreta, Eforie, Fagaras, Giurgiu, Hirsova,Iasi, Lugoj, Mehadia, Neamt, Oradea, Pitesti, Rimnicu_Vilcea, Sibiu, Timisoara,Urziceni, Vaslui, Zerind}; int arcs[N][N] = {0}; // 定义两个城市间的距离 // 定义两个城市间的直线距离,即最短距离,小于等于实际距离 int line[N] = {366, 0, 160, 242, 161, 176, 77, 151, 226, 244, 241, 234, 380, 10, 193, 253, 329, 80, 199, 374}; int g[N] = {0}; // 从初始节点到当前节点的代价 // 初始化问题状态 void init() { // 定义两个城市间的距离 { arcs[Zerind][Oradea] = 71; arcs[Zerind][Arad] = 75; arcs[Arad][Sibiu] = 140; arcs[Arad][Timisoara] = 118; arcs[Oradea][Sibiu] = 151; arcs[Timisoara][Lugoj] = 111; arcs[Lugoj][Mehadia] = 70; arcs[Mehadia][Dobreta] = 75; arcs[Dobreta][Craiova] = 120; arcs[Sibiu][Fagaras] = 99; arcs[Sibiu][Rimnicu_Vilcea] = 80; arcs[Rimnicu_Vilcea][Pitesti] = 97; arcs[Rimnicu_Vilcea][Craiova] = 146; arcs[Craiova][Pitesti] = 138; arcs[Pitesti][Bucharest] = 101; arcs[Fagaras][Bucharest] = 211; arcs[Bucharest][Giurgiu] = 90; arcs[Bucharest][Urziceni] = 85; arcs[Urziceni][Hirsova] = 98; arcs[Hirsova][Eforie] = 86; arcs[Urziceni][Vaslui] = 142; arcs[Vaslui][Iasi] = 92; arcs[Iasi][Neamt] = 87; } int i, j; for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(arcs[i][j] > 0) { arcs[j][i] = arcs[i][j]; } else if(arcs[j][i] > 0) { arcs[i][j] = arcs[j][i]; } else if(i != j) { arcs[i][j] = MaxInt; arcs[j][i] = MaxInt; } } } } // 转换成城市名 void transform(int city) { switch(city) { case Arad: printf("%s\n", "Arad"); break; case Bucharest: printf("%s\n", "Bucharest"); break; case Craiova: printf("%s\n", "Craiova"); break; case Dobreta: printf("%s\n", "Dobreta"); break; case Eforie: printf("%s\n", "Eforie"); break; case Fagaras: printf("%s\n", "Fagaras"); break; case Giurgiu: printf("%s\n", "Giurgiu"); break; case Hirsova: printf("%s\n", "Hirsova"); break; case Iasi: printf("%s\n", "Iasi"); break; case Lugoj: printf("%s\n", "Lugoj"); break; case Mehadia: printf("%s\n", "Arad"); break; case Neamt: printf("%s\n", "Neamt"); break; case Oradea: printf("%s\n", "Oradea"); break; case Pitesti: printf("%s\n", "Pitesti"); break; case Rimnicu_Vilcea: printf("%s\n", "Rimnicu Vilcea"); break; case Sibiu: printf("%s\n", "Sibiu"); break; case Timisoara: printf("%s\n", "Timisoara"); break; case Urziceni: printf("%s\n", "Urziceni"); break; case Vaslui: printf("%s\n", "Vaslui"); break; case Zerind: printf("%s\n", "Zerind"); break; } } // 打印解的路径 void show(int *Path) { int i; printf("解的路径如下\n"); for(i = 0; Path[i] != -1; i++) { transform(Path[i]); // 打印当前节点 } } // 启发式算法 void Astar(int V0, int VN) { printf("Astar start\n"); int i, v, w, min, cost; int S[N]; // 记录从源点V0到终点Vi是否已被确定为最短路径长度 int Path[N]; // 记录从源点V0到终点Vi的当前最短路径长度上Vi的直接前驱节点号 for(i = 0; i < N; i++) { S[i] = 0; // 初始时所有节点都没有被加入解路径 Path[i] = -1; // 初始化解的路径 g[i] = arcs[V0][i]; // 初始化节点到当前节点的代价 } cost = 0; S[V0] = 1; // 标记已经选出的最小的节点 Path[0] = V0; // 把选出的节点加入到解的路径中 for(i = 1; i < N; i++) { v = V0; min = MaxInt; // 从不在解的路径中的节点组成的节点集和当前节点的后继节点的组成的节点集的交集中 // 选择出估计函数最小的节点,作为下一个要拓展的节点 for(w = 0; w < N; w++) { if(!S[w] && arcs[Path[i-1]][w] > 0 && arcs[Path[i-1]][w] < MaxInt) { if(g[w]+ line[w] < min) { v = w; min = g[w]+ line[w]; } } } S[v] = 1; // 标记已经选出的最小的节点 Path[i] = v; // 把选出的节点加入到解的路径中 printf("本次拓展节点:"); transform(v); printf("估计函数值:%d\n", min); cost += arcs[Path[i-1]][v]; // 累加实际代价 // 更改当前节点到剩下不在解的路径中的代价 // 这里直接修改,不需要比较g[w] 与 g[v] + arcs[v][w]的大小 // 这里这里没有采用open表和close表,所以为了避免回溯的问题,直接修改 for(w = 0; w < N; w++) { if(!S[w]) { g[w] = g[v] + arcs[v][w]; } } // 如果选出的节点就是目标节点,结束 if(Path[i] == VN) { printf("Astar finish\n\n"); show(Path); printf("总共的代价:%d\n", cost); break; } } } int main(void) { init(); Astar(Zerind, Bucharest); return 0; }
实验分析:
略!
具体请查看我的博客里对应的算法描述,十分详细。如果想看搜索算法大全的可以看这篇,七种搜索算法大集合:http://t.csdn.cn/8vifa