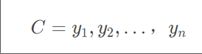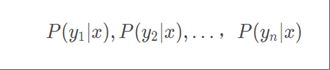广州大学机器学习与数据挖掘实验二
实验二 逻辑回归与朴素贝叶斯分类
一、 实验目的
本实验课程是计算机、人工智能、软件工程等专业学生的一门专业课程，通过实验，帮助学生更好地掌握数据挖掘与机器学习相关概念、技术、原理、应用等；通过实验提高学生编写实验报告、总结实验结果的能力；使学生对机器学习模型、算法等有比较深入的认识。要掌握的知识点如下：
- 掌握机器学习中涉及的相关概念、模型、算法；
- 熟悉机器学习模型训练、验证、测试的流程；
- 熟悉常用的数据预处理方法；
- 掌握逻辑回归、贝叶斯分类的表示、求解及编程。
二、基本要求
- 实验前，复习《数据挖掘与机器学习》课程中的有关内容。
- 准备好实验数据，编程完成实验内容，收集实验结果。
- 独立完成实验报告。
三、实验软件
推荐使用Python编程语言（允许使用numpy库，需实现详细实验步骤，不允许直接调用scikit-learn中回归、分类等高层API）。
四、实验内容：
基于Adult数据集，完成关于收入是否大于50K的逻辑回归分类、朴素贝叶斯模型训练、测试与评估。
1 准备数据集并认识数据
下载Adult数据集
http://archive.ics.uci.edu/ml/datasets/Adult
了解数据集各个维度特征及预测值的含义
2 探索数据并预处理数据
观察数据集各个维度特征及预测值的数值类型与分布
预处理各维度特征，参考：https://blog.csdn.net/SanyHo/article/details/105304292
3 训练模型
编程实现训练数据集上逻辑回归模型的梯度下降参数求解、朴素贝叶斯参数统计
4 测试和评估模型
在测试数据集上计算所训练模型的准确率、AUC等指标
五、学生实验报告
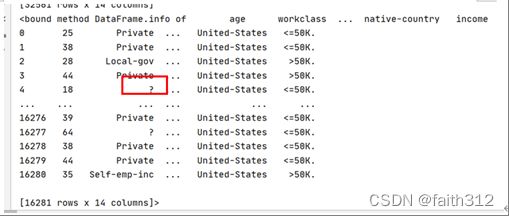
因为在该实验中我定义的X矩阵的行数代表训练集有多少条，列数代表特征个数，如下图：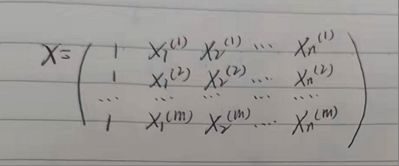
与以下算法原理解释中的X所代表的矩阵行列有不同，所以在编码时不会完全根据原理中的式子进行编码，而是都会做些相应的更改，但最后实验结果不会受到影响。
（1）简要介绍逻辑回归分类的原理
逻辑回归的本质就是线性回归的一种。名称虽然是逻辑回归，但却是解决二分类问题的一种最常用方法之一。
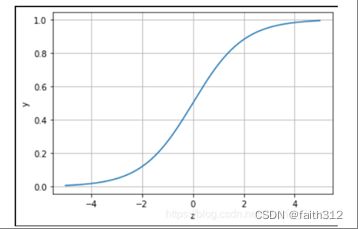
①Sigmoid函数，也称为逻辑函数（Logistic function）：
其函数曲线如下图所示：
可以发现 Logistic 函数是单调递增函数，并且在z=0的时候取值为0.5，并且logi(⋅)函数的取值范围为( 0 , 1 )
②逻辑回归的假设函数形式：
其中x是我们输入的特征向量，θ是我们所求的参数向量。
③逻辑函数所做的假设是：
上式的意思是给定x和θ的条件下y = 1和y = 0的概率。
④代价函数：
求l(θ)的最大值，即为求代价函数J（θ）的最小值
⑤基于上述代价函数对参数向量θ进行更新：
即为：
对于模型的训练而言：实质上来说就是利用训练集数据求解出对应模型的特定θ向量。从而得到一个针对于训练集数据的特征逻辑回归模型。
（2）简要介绍朴素贝叶斯分类的原理
朴素贝叶斯算法是一种生成学习算法（generative learning algorithms），所谓生成学习算法是指对p(x|y)与p(y)同时建模，对不同类别的数据集分别建模，看新输入的数据更符合哪类模型，该数据便属于哪一类。
如何根据给出数据判断数据属于哪一类，原理如下：
①设
为一个待分类箱，而每个a为x的一个特征属性
②有类别集合
③计算
④如果
则
如何计算第③步中的各个条件概率，我们可以：
1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计,即先验概率。
3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：
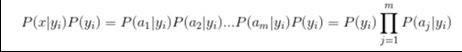
（3）程序清单（包含详细求解步骤）
逻辑回归分类：
①要引进的库
②导入数据集（分为训练集和测试集），观察数据特点
因为是从txt文件中读取的数据，所以将每一列特征的名字加上。
train_set.info()
print(test_set)
有6个特征是int64类型，9个特征是object类型，发现测试集上有出现值为?的缺失。
③预处理各维度特征
1’处理缺失值（将含有缺失值的数据扔掉）
2’因为fnlgwt列表示为数据的编号，对分类的结果不太有关联，所以删除
3’将object类型的列进行标签编码，转为int类型
④将训练集和测试集分别整理成拟合函数中的X_train矩阵，y_train矩阵和X_test矩阵,y_test矩阵
输出为：
⑤进行逻辑回归参数求解
⑥计算准确率
输出的准确率为：
朴素贝叶斯分类
①引入库，导入数据集，做法与逻辑回归的相同
②数据初步处理
与逻辑回归的数据处理相比多了删除EduNum的操作
③对连续值进行处理
1’将age属性划分为4个区间 0-25 25-50 50-75 75-100
2’将caption-gain属性 划分为=0, >0两类
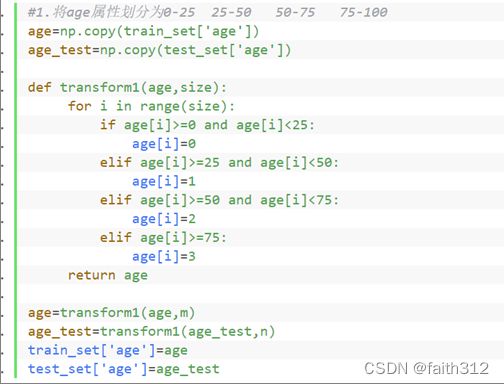
3’将captional-loss属性 划分为>0 =0两类
4’将hours-per-week属性划分为 <40 ==40 >40三类
5’将Country属性划分为USA not USA两类
⑤将object类型的特征列都进行标签编码
⑥根据income属性值将训练集分为两类，一类为income<50k 一类为income>=50K
⑦计算income的两个类别的先验概率P（c）
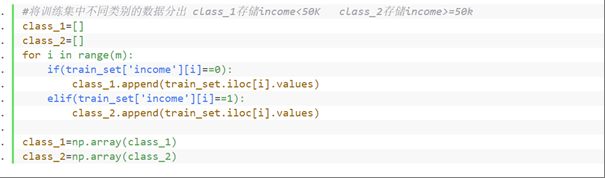
⑧定义能计算某个类型数据集中各特征列中每个出现的值及其次数的函数（返回counting table）
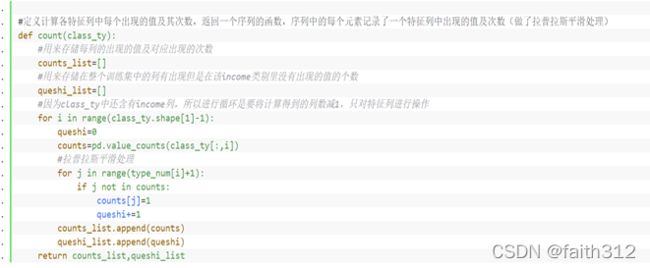
⑨定义能计算条件概率P(x|c)的函数（进行了拉普拉斯平滑处理）
⑩计算P（c|x）
⑪计算测试集上的准确率
（4）展示实验结果
逻辑回归算法输出的测试集上准确率为：
朴素贝叶斯算法输出的测试集上的准确率为：
（5）讨论实验结果，分析各个特征与目标预测类别的正负相关性
①从两个算法最后的准确率来看，逻辑回归算法在测试集上训练模型的准确率比朴素贝叶斯的要稍好些。
②逻辑回归算法和朴素贝叶斯算法对比：
1’逻辑回归在训练时，不管特征之间有没有相关性，它都能找到最优的参数。而在朴素贝叶斯中，我们直接给定特征相互独立的严格设定。
2’小数据上面朴素贝叶斯分类器可以取得更好的效果，随着数据的增多、特征维度的增大，逻辑回归的效果更好
3’朴素贝叶斯没有优化参数这一步，通过训练数据可以直接得到一个counting table。
③在训练集上分析一下各特征与目标预测类别income的相关系数
输出结果如下：
可以发现education-num与income类别的相关系数最大，其次较大的是age和hours-per-week。在现实生活中，学历，年龄以及每周工作的时长确实极大地影响了工资高低。
（6）源代码
逻辑回归
import numpy as np
import pandas as pd
from sklearn.preprocessing import LabelEncoder
#导入数据集 （数据集被放在一个oldData文件夹中）
train_set=pd.read_csv('oldData/adult.data',header=None,names=['age','workclass','fnlwgt','education',
'education-num','marital-status',
'occupation','relationship','race',
'sex','capital-gain','capital-loss',
'hours-per-week','native-country','income'])
train_set.info()
test_set=pd.read_csv('oldData/adult.test',header=None,names=['age','workclass','fnlwgt','education',
'education-num','marital-status',
'occupation','relationship','race',
'sex','capital-gain','capital-loss',
'hours-per-week','native-country','income'])
test_set.info()
print(test_set)
#处理缺失值 将含有值'？'的数据行去掉
for i in train_set.columns:
test_set=test_set[test_set[i]!=' ?']
train_set=train_set[train_set[i]!=' ?']
print(test_set)
#删除fnlgwt列
train_set.drop('fnlwgt',axis=1,inplace=True)
test_set.drop('fnlwgt',axis=1,inplace=True)
#将object类型都进行标签编码 都变成Int32类型
s=(train_set.dtypes=='object')
object_cols=list(s[s].index)
label_encoder=LabelEncoder()
for col in object_cols:
train_set[col]=label_encoder.fit_transform(train_set[col])
test_set[col] = label_encoder.fit_transform(test_set[col])
# print(train_set.info())
# print(test_set.info())
#看一下各特征与income的相关系数
temp=train_set.copy()
corr=temp.corr()
score=corr['income'].sort_values()
print(score)
#将Income分出
cols=train_set.shape[1]
X_train,y_train=train_set.iloc[:,:cols-1].values,np.matrix(train_set['income'].values)
X_test,y_test=test_set.iloc[:,:cols-1].values,np.matrix(test_set['income'].values)
#m为训练集的行数
m=X_train.shape[0]
#n为测试集行数
n=X_test.shape[0]
#加入一列值全为1的特征列
X_train=np.c_[np.ones(m),X_train]
X_test=np.c_[np.ones(n),X_test]
#进行转置，方便后续计算
y_train=y_train.T
y_test=y_test.T
print(X_train.shape)
print(y_train.shape)
#---------------------数据预处理完毕----------------------
#---------------------逻辑回归-----------------------
#定义逻辑回归所需参数
alpha=0.01
theta=(np.matrix([0,0,0,0,0,0,0,0,0,0,0,0,0,0])).T
iter=1000
print(theta.shape)
#定义逻辑函数
def sigmoid(z):
return 1/(1+np.exp(-z))
#定义梯度上升杉树
def gradient_boost(theta, alpha):
for i in range(iter):
theta=theta+(alpha/m)*(X_train.T@(y_train-sigmoid(X_train@theta)))
# print(theta)
return theta
#求解θ
theta=gradient_boost(theta,alpha)
print(theta)
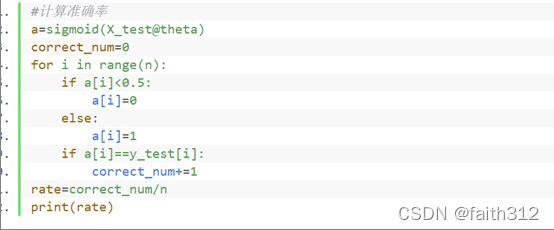
#计算准确率
a=sigmoid(X_test@theta)
correct_num=0
for i in range(n):
if a[i]<0.5:
a[i]=0
else:
a[i]=1
if a[i]==y_test[i]:
correct_num+=1
rate=correct_num/n
print(rate)
朴素贝叶斯（其中拉普拉斯的处理有问题）
import numpy as np
import pandas as pd
from sklearn.preprocessing import LabelEncoder
#导入数据集
train_set=pd.read_csv('oldData/adult.data',header=None,names=['age','workclass','fnlwgt','education',
'education-num','marital-status',
'occupation','relationship','race',
'sex','capital-gain','capital-loss',
'hours-per-week','native-country','income'])
train_set.info()
# print(train_set)
test_set=pd.read_csv('oldData/adult.test',header=None,names=['age','workclass','fnlwgt','education',
'education-num','marital-status',
'occupation','relationship','race',
'sex','capital-gain','capital-loss',
'hours-per-week','native-country','income'])
test_set.info()
# print(test_set)
#处理缺失值 将含有值'？'的数据行去掉
for i in train_set.columns:
test_set=test_set[test_set[i]!=' ?']
# train_set=train_set[train_set[i]!=' ?']
#删除fnlgwt列
train_set.drop('fnlwgt',axis=1,inplace=True)
test_set.drop('fnlwgt',axis=1,inplace=True)
#Eductaion和EduNum特征相似，可以删除EduNum
train_set.drop(['education-num'],axis=1,inplace=True)
test_set.drop(['education-num'],axis=1,inplace=True)
#m,n分别为训练集和测试集的行数
m=train_set.shape[0]
n=test_set.shape[0]
#-----------------------将连续值变为离散值-----------------------
#1.将age属性划分为0-25 25-50 50-75 75-100
age=np.copy(train_set['age'])
age_test=np.copy(test_set['age'])
def transform1(age,size):
for i in range(size):
if age[i]>=0 and age[i]<25:
age[i]=0
elif age[i]>=25 and age[i]<50:
age[i]=1
elif age[i]>=50 and age[i]<75:
age[i]=2
elif age[i]>=75:
age[i]=3
return age
age=transform1(age,m)
age_test=transform1(age_test,n)
train_set['age']=age
test_set['age']=age_test
# print(train_set['age'])
#2.将caption-gain属性 >0的值都用1替换 =0的值都用0替换
gain=np.copy(train_set['capital-gain'])
gain_test=np.copy(test_set['capital-gain'])
def transform2(gain,size):
for i in range(size):
if gain[i]==0:
gain[i]=0
elif gain[i]>0:
gain[i]=1
return gain
gain=transform2(gain,m)
gain_test=transform1(gain_test,n)
train_set['capital-gain']=gain
test_set['capital-gain']=gain_test
# print(train_set['capital-gain'])
#3.将captional-loss属性 划分为>0 =0两类
loss=np.copy(train_set['capital-loss'])
loss_test=np.copy(test_set['capital-loss'])
loss=transform2(loss,m)
loss_test=transform1(loss_test,n)
train_set['capital-loss']=loss
test_set['capital-loss']=loss_test
# print(train_set['capital-loss'])
#4.将housr-per-week划分为 <40 ==40 >40
hours=np.copy(train_set['hours-per-week'])
hours_test=np.copy(test_set['hours-per-week'])
def transform3(hours,size):
for i in range(size):
if hours[i] < 40:
hours[i] = 0
elif hours[i] == 40:
hours[i] = 1
elif hours[i] >40:
hours[i]=2
return hours
hours=transform3(hours,m)
hours_test=transform3(hours_test,n)
train_set['hours-per-week']=hours
test_set['hours-per-week']=hours_test
#print(train_set['hours-per-week'])
#5.将Country划分为USA not USA两类
cty=np.copy(train_set['native-country'])
cty_test=np.copy(test_set['native-country'])
def transform4(cty,size): #多了个空格的问题
for i in range(size):
if cty[i] ==" United-States":
cty[i] = 0
elif cty[i] != " United-States":
cty[i] = 1
return cty
cty=transform4(cty,m)
cty_test=transform4(cty_test,n)
train_set['native-country']=cty
test_set['native-country']=cty_test
# print(train_set['native-country'])
print(train_set.info())
print(train_set)
#将object类型都进行标签编码 都变成Int32类型 都变为了离散值
s=(train_set.dtypes=='object')
object_cols=list(s[s].index)
label_encoder=LabelEncoder()
for col in object_cols:
train_set[col]=label_encoder.fit_transform(train_set[col])
test_set[col] = label_encoder.fit_transform(test_set[col])
type_num=train_set.max()
# print(a)
# print(a[2])
#----------------------朴素贝叶斯--------------------------
# print(train_set[1])
#将训练集中不同类别的数据分出 class_1存储income<50K class_2存储income>=50k
class_1=[]
class_2=[]
for i in range(m):
if(train_set['income'][i]==0):
class_1.append(train_set.iloc[i].values)
elif(train_set['income'][i]==1):
class_2.append(train_set.iloc[i].values)
class_1=np.array(class_1)
class_2=np.array(class_2)
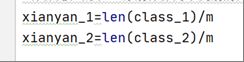
#计算先验概率 分别计算两个类别的先验概率
xianyan_1=len(class_1)/m
xianyan_2=len(class_2)/m
#保存每列所含的种数
type_num=train_set.max()
# print(type_num)
#定义计算各特征列中每个出现的值及其次数，返回一个序列的函数，序列中的每个元素记录了一个特征列中出现的值及次数（做了拉普拉斯平滑处理）
def count(class_ty):
#用来存储每列的出现的值及对应出现的次数
counts_list=[]
#用来存储在整个训练集中的列有出现但是在该income类别里没有出现的值的个数
queshi_list=[]
#因为class_ty中还含有income列，所以进行循环是要将计算得到的列数减1，只对特征列进行操作
for i in range(class_ty.shape[1]-1):
queshi=0
counts=pd.value_counts(class_ty[:,i])
#拉普拉斯平滑处理
for j in range(type_num[i]+1):
if j not in counts:
counts[j]=1
queshi+=1
counts_list.append(counts)
queshi_list.append(queshi)
return counts_list,queshi_list
#定义计算条件概率P(xi|c)的函数
def p_x_c(class_ty,counts_list,queshi_list,linedata):
p_list = []
for i in range(class_ty.shape[1]-1):
if(linedata[i] not in counts_list[i]):
counts_list[i][linedata[i]]=1
queshi_list[i]+=1
p1 = counts_list[i][linedata[i]]/(len(class_ty)+queshi_list[i])
p_list.append(p1)
return p_list
test_set=np.array(test_set)
train_set=np.array(train_set)
counts_list1,queshi_list1=count(class_1)
counts_list2,queshi_list2=count(class_2)
#用来装用不同income类型形成的生成模型所求出的p(c|xi)值
y_test_list1=[]
y_test_list2=[]
#用来装预测的income分类值
y_pred=[]
#计算测试集上数据的p(c|x)
for i in range(len(test_set)):
p_list1=p_x_c(class_1,counts_list1,queshi_list1,test_set[i])
p_list2=p_x_c(class_2,counts_list2,queshi_list2,test_set[i])
# print(p_list1)
y1 = xianyan_1
y2=xianyan_2
for j in range(train_set.shape[1]-1):
y1=y1*p_list1[j]
y2=y2*p_list2[j]
y_test_list1.append(y1)
y_test_list2.append(y2)
#根据p(c|xi)判断该行数据属于哪类income(0,1)
for i in range(len(test_set)):
if(y_test_list1[i]>y_test_list2[i]):
y_pred.append(0)
else:
y_pred.append(1)
#计算准确率
correct_num=0
for i in range(len(test_set)):
if(y_pred[i]==test_set[i,-1]):
correct_num=correct_num+1
rate=correct_num/len(test_set)
print(rate)