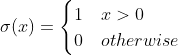多层感知机multiLayerPercetrons

目录

1. 感知机：

2. 常用非线性的激活函数

​3. 多层感知机——多隐藏层

4. 代码实践

---

1. 感知机：

感知机(perceptron)是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别。

线性模型在处理一些问题时好用，但是在处理XOR问题时就出现了问题。

因为线性模型无法将①④和②③同时分类，但是通过增加隐藏层来逐步分类，如上图黄线和蓝线，两个步骤就能分出来。所用感知机为单分类单隐藏层感知机。

 隐藏层需要非线性的激活函数，不然本质的运算还是线性模型。

2. 常用非线性的激活函数

激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活。它们是将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。

2.1 Sigmoid激活函数

将输入投影到（0,1），   

 

 

 2.2 Tanh激活函数

将输入投影到(-1,1)，

2.3  ReLU激活函数，计算简单，速度比Sigmoid和Tanh激活函数快。

3. 多层感知机——多隐藏层

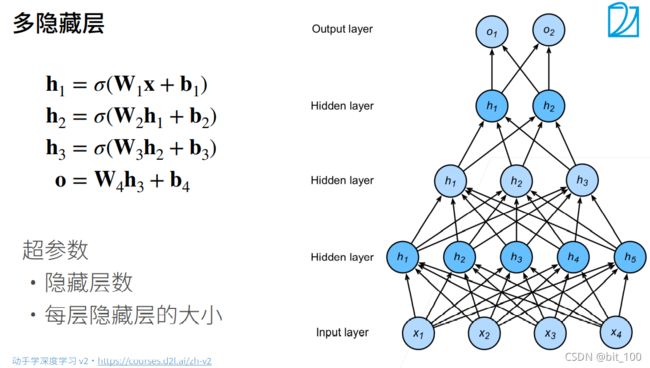 多层隐藏层的感知机，表达能力更强，因为层数越多其层与层之间提取的特征越精细，对于以原始数据的抽象逐层抽象，对于原始数据的损失不会因为层数少而突然损失过大。

但是因为层与层之间是全连接的，并且层数越多需要耿总的超参数也越多，使得开销增大。

4. 代码实践

import torch
from torch import nn
import d2l
from d2l import common as d2l

batch_size = 256

# 读取数据
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#实现一个具有单隐藏层的多层感知机，包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(
    torch.randn(num_inputs, num_hiddens, requires_grad=True))  # 784 x 256
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True))  # 256 x 10
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

# 实现ReLU激活函数
def relu(X):
    a = torch.zeros_like(X)  # a全为零，X.shape
    return torch.max(X, a)

#实现模型
def net(X):
    X = X.reshape((-1, num_inputs))  #batch_size x num_inputs 256 x 784
    H = relu(X @ W1 + b1)    #@矩阵乘法，用matmul(X, W1)也可以
    return ( H @ W2 + b2 )

# 损失
loss = nn.CrossEntropyLoss()


# 优化器
leaning_rate = 0.01
def optimizer_func():
    return torch.optim.SGD(params, lr=leaning_rate)


# 训练
def epoch_train(net, train_iter, loss, updater):
    if isinstance(net, torch.nn.Module):
        net.train()
    metric = d2l.Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):  # 如果是pytorch的optimizer的话，就
            updater.zero_grad()  # 先把梯度置为零
            l.backward()  # 然后计算梯度
            updater.step()  # 更新参数
            metric.add(  # 累加loss,准确数，样本数
                float(l) * len(y), d2l.accuracy(y_hat, y),
                y.size().numel())
    return metric[0] / metric[2], metric[1] / metric[2]  # 返回的是  loss/样本数   所有正确的样本/样本数


def train(net, train_iter, test_iter, loss, num_epochs, updater):
    for epoch in range(num_epochs):
        train_metrics = epoch_train(net, train_iter, loss, updater)
        train_loss, train_acc = train_metrics[0], train_metrics[1]
        test_acc = d2l.evaluate_accuracy(net, test_iter)
        print('epoch： %d, loss： %.4f, train_acc： %.3f, test_acc： %.3f' % (epoch + 1, train_loss, train_acc, test_acc))




#实现
num_epochs = 20
train(net, train_iter, test_iter, loss, num_epochs, optimizer_func())

 ！！！在实现过程中遇到一个问题

SGD优化器，直接调用torch.optim.SGD赋值给变量optimizer_train，就产生了SGD object is not callable 的问题。

# 优化器
leaning_rate = 0.01
optimizer_train=torch.optim.SGD(params, lr=leaning_rate)

定义成函数，然后传参函数名就可以。疑惑还存在。

# 优化器
leaning_rate = 0.01
def optimizer_func():
    return torch.optim.SGD(params, lr=leaning_rate)

详细参考李沐老师的书籍《动手学深度学习》

4.1. 多层感知机 — 动手学深度学习 2.0.0-alpha2 documentation (d2l.ai)https://zh-v2.d2l.ai/chapter_multilayer-perceptrons/mlp.html10 多层感知机 + 代码实现 - 动手学深度学习v2_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1hh411U7gn?p=2图片来自李沐老师的slides

part-0_13.pdf (d2l.ai)https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_13.pdf