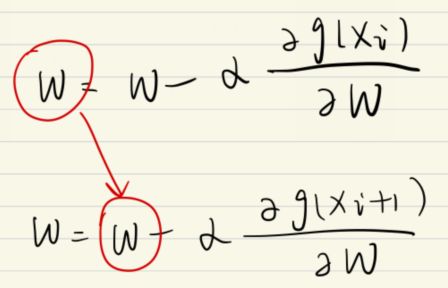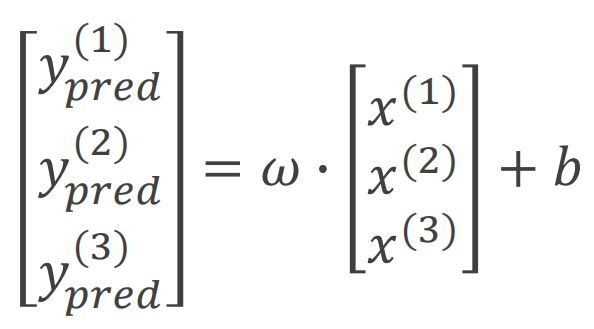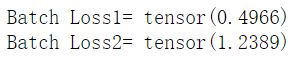【刘二大人 - PyTorch深度学习实践】学习随手记（一）
目录
1. Overview
1、Human Intelligence
2、Machine Learning
3、How to develop learning system?
4、Traditional Machine Learning Strategy
5、SVM挑战
6、Brief History of Neural Network
7、流行的深度学习框架
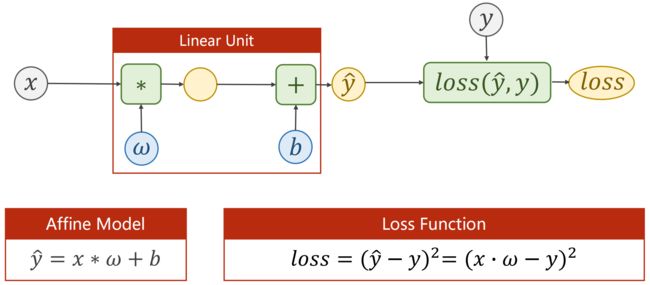
2. Linear Model（线性模型）
模型为 y = w * x 的代码：
模型为 y = w * x + b 的代码：
3. Gradient Descent（梯度下降算法）
1、寻找最优w值的几种方法
2、梯度下降法（Gradient Descent Algorithm）
3、随机梯度下降法（Stochastic Gradient Descent Algorithm）
4. Back Propagation（反向传播）
1、计算图
2、Tensor in PyTorch
5. Linear Regression with Pytorch（用Pytorch实现线性回归）
1、Before：线性模型如何训练、如何更新权重
2、Now：如何构造神经网络 nn.Module、损失函数 loss、随机梯度下降的优化器
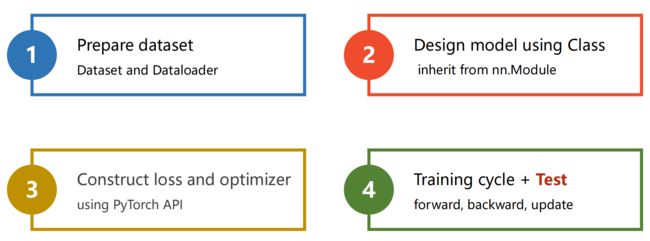
（1）Prepare dataset
（2）设计模型
（3）构造损失函数和优化器
（4）训练周期
Exercise
6. Logistic Regression（逻辑斯蒂回归）
分类问题中的数据集：
Sigmoid 函数：
逻辑回归模型
损失函数（Binary Cross Entropy，二分类交叉熵）
逻辑回归的完整代码
7. Multiple Dimension Input（处理多维特征的输入）
Mini-Batch（N个样本）
例子：糖尿病预测
8. Dataset and Dataloader（加载数据集）
区分 Epoch Batch-Size Iteration
Dataset：提供索引和 len()
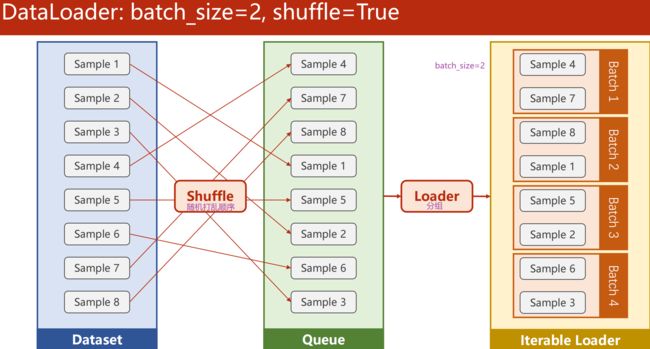
DataLoader：batch_size=2，shuffle=True
如何定义数据集
例子：糖尿病数据集（Diabetes Dataset）
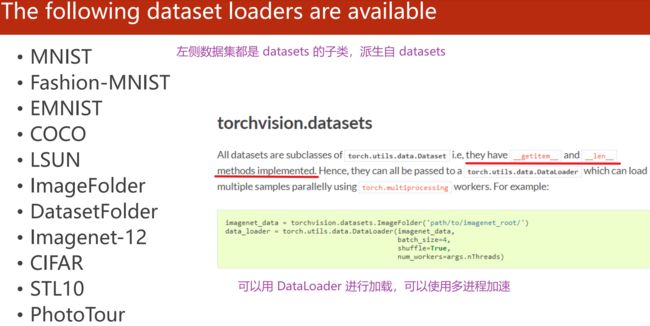
torchvision.datasets
Exercise
9. Softmax Classifier（多分类问题）
十分类问题神经网络应该怎么设计？
Loss Function - Cross Entropy
对比：CrossEntropyLoss（交叉熵损失） 和 NLLLoss（NLL损失）
Mini-Batch
对 MNIST 数据集构建分类器
Exercise
1. Overview
PyTorch 是一种深度学习框架，代码版本：Pytorch 0.4
1、Human Intelligence
-
推理（Infer）：外部信息或已有信息输入 ——> 决策 ——> 推理
-
预测（Prediction）：把视觉上接收到的信息转换成抽象概念的过程
把真实世界的实体与抽象概念（实例化后才易理解）联系起来
2、Machine Learning
- 推理（Infer）：把用来作推理的大脑换为算法（AI）
- 预测（Prediction）：用算法把视觉信息或自然语言文本转换为抽象概念
从数据集中找算法 ——> 提模型 ——> 拿数据训练 ——> 验证效果 ——> 部署
监督学习（Supervised）—— Labeled Dataset（打上标签的数据）
基于统计的方法（如最大似然、最大后验）
（1）算法设计思维方式：
- 穷举法
- 贪心法：每一步只选当前看来最好的选择，如梯度下降
- 分治法：一分为二
- 动态规划
（2）分类：
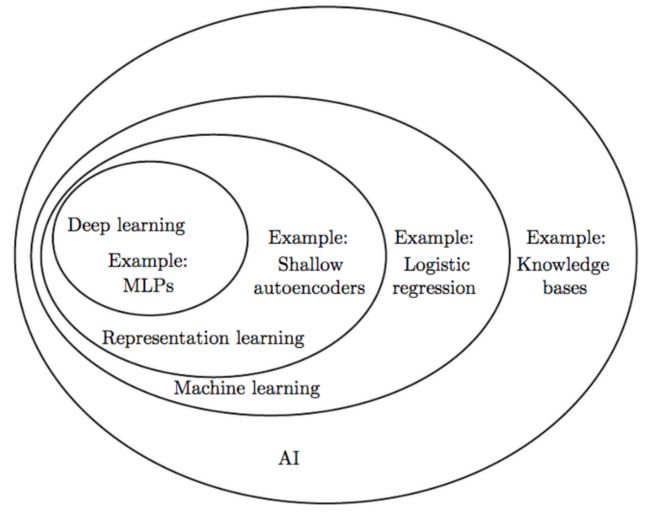
- AI > Machine Learning > Representation Learning > Deep Learning
- AI：如知识库（Knowledge Bases）、机器学习、机器视觉（Machine Vision）、因果推断、NLP
- Machine Learning：如逻辑回归（Logistic Regression）
- Representation Learning（表示学习）：一种特征提取（原始数据特征特别多，用一种更好的方法表示数据）。如：浅层自动编码器（Shallow Autoencoders）
- Deep Learning：如多层感知机（MLPs）、卷积/循环神经网络。缺陷主要是可解释性差
3、How to develop learning system?
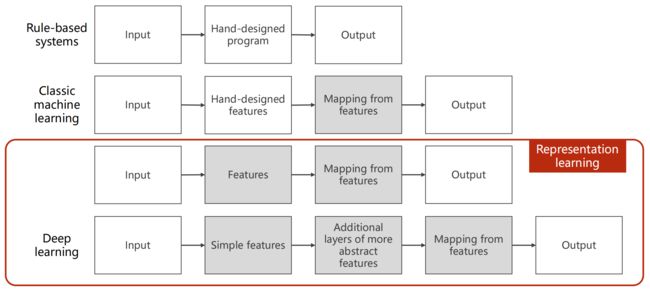
（1）基于规则（Rule-based）：手工设计程序
- 依赖规则的制定，要有很强的背景知识，复杂目标规则难以制定
- 例：程序求原函数
构建知识库 ——> 等价变形规则 ——> 三角变换 - 如图搜索、树搜索等
（2）经典机器学习：
- 输入（关系型数据表中的记录或无结构输入）——> 手工提取特征 ——> 把向量与输出之间建立一个线性的映射
- 手工提取特征：
法1：筛选
法2：输入（图像、文本、语音等）变为向量/张量
--------------------------------------------------------------------------------------------------------------------------------
（3）表示学习：
- 为什么要特征提取？
维度诅咒：每一条数据样本（input）的特征越多，对样本数量的需求就越多（这样才可以满足大数定律，满足原分布） - 学习提取出来的特征的向量，以及由高维空间到低维空间的表示（由高维空间压缩到低维空间，线性/非线性的映射），尽量保持高维空间的度量信息
- 表示学习/降维：学习器面临维度诅咒，维度越高，需要数据量越大
- 从数据训练中得到算法
（4）深度学习：
- 原来要训练专门的特征提取器，深度学习只用原始特征（非常简单的特征），做变换
- 传统表示学习方法：特征（无标签）与学习器（有标签）是分开训练的，机器学习中的无监督学习（无标签）即做特征提取的训练
- 深度学习是统一训练，是端到端的训练过程（End2End），即输入 ——> 模型（整个一起训练）——> 输出
4、Traditional Machine Learning Strategy
5、SVM挑战
- 手工设计特征的限制
- 不能很好地应对大数据集
- 越来越多的应用需要解决无结构数据（图像、文本、声音...）
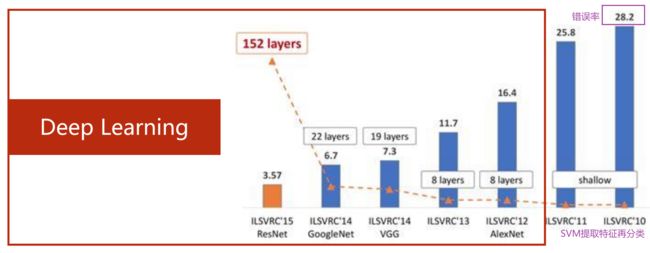ImageNet Large Scale Visual Recognition Challenge
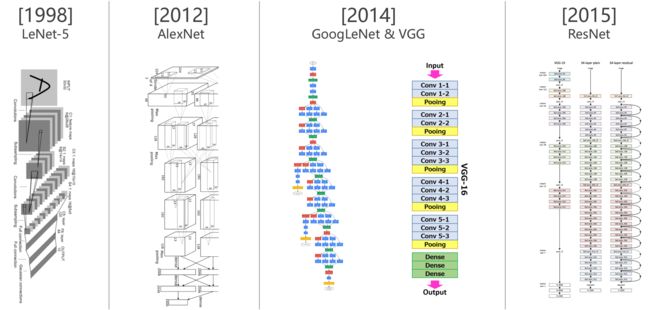
6、Brief History of Neural Network
- 神经网络来源：神经科学
- 深度学习来源：数学与工程学
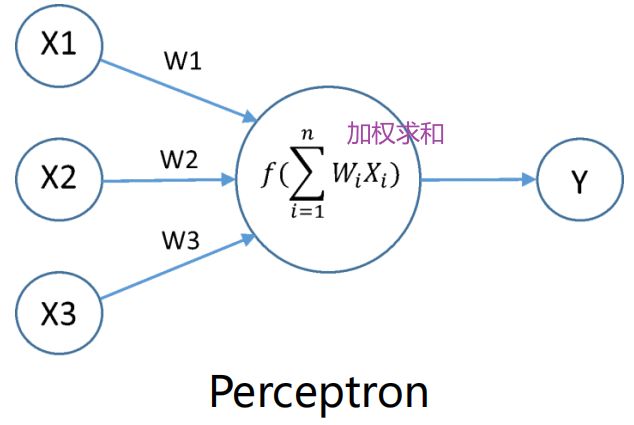
（1）感知机
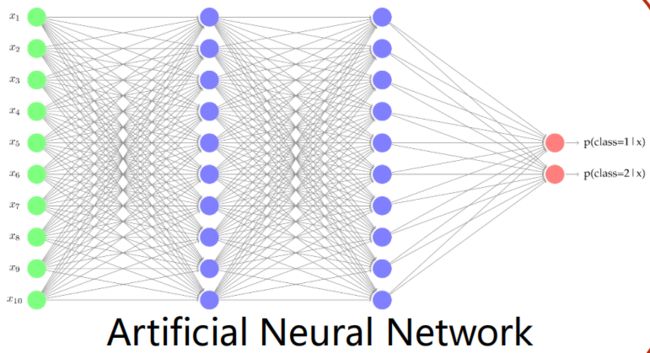
（2）人工神经网络
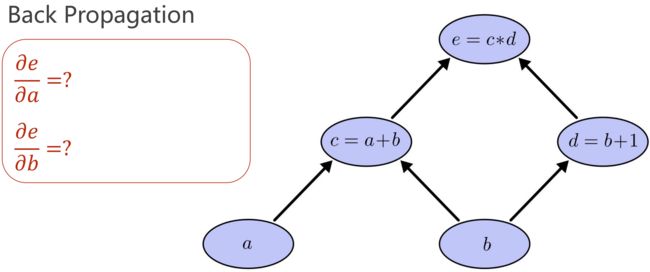
（3）反向传播（Back Propagation）：求偏导
核心：计算图
先正向计算：前馈过程、原子计算
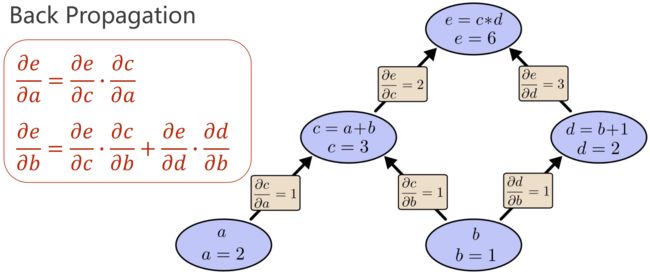链式法则
基本原子的偏导确定下来 ——> 计算图里的传播导数
模型易拓展，灵活性好
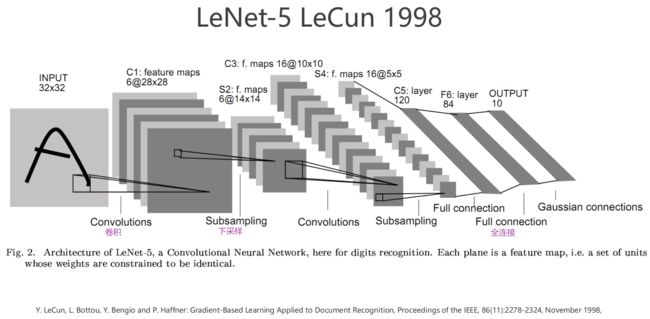
（4）LeNet-5 识别手写邮政编码
神经网络得以发展的三大因素：
- 算法 Algorithm
- 数据 Data
- 算力提升 Computation
7、流行的深度学习框架
- TensorFlow：Static Graph（静态图），灵活性低
- Pytorch：Dynamic Graph，灵活、易调试
- MxNet
安装Pytorch后：
- Win+R输入cmd，进入命令行
- 首先激活pytorch环境，输入
conda activate pytorch激活pytorch环境后可以看到前面有个 (pytorch)
-
先输入
python，再输入
import torch，最后输入
print(torch.__version__)结果如图所示：
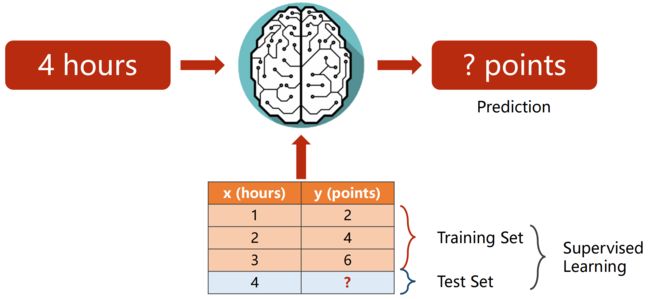
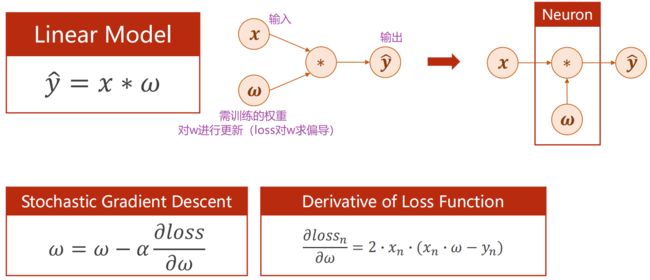
2. Linear Model（线性模型）
准备Dataset ——> 选择/设计Model ——> 训练（人工/自动）——> 应用：infer（推理）
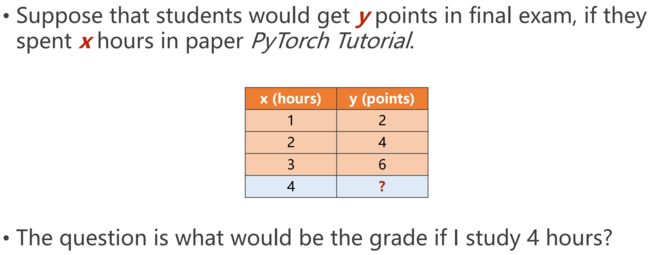前三个数据为training，最后一个为test
监督学习
模型看不到y的两种情况：
- 测试test
- 模型上线后的推理
整个数据集分为：
（1）训练集：看得到x和y
实际将训练集再一分为二：
- 训练集：训练（过拟合：训练集误差很小，但也学了噪声）
- 开发集：评估（又叫验证集）
（2）测试集：只看得到x（判断模型的泛化能力，即对没见过的图像能否进行较好的识别）
---------------------------------------------------------------------------------------------------------------------------------
选择模型：一般先拿线性模型试试，效果不好再拿其他复杂的模型
如何找到最优权重w？
- 机器学习一般首先w取随机数（w = random value）
- 取了一个权重w后，评估偏移/计算误差（Evaluate Model Error）
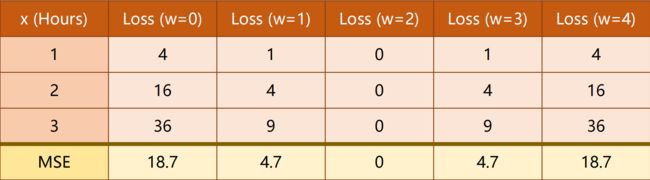
对于一个样本来说： Loss Function
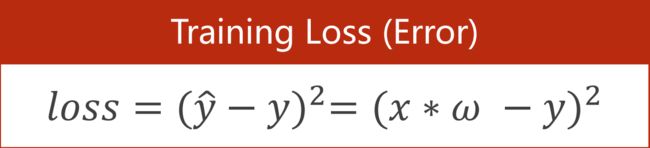Loss用来评估模型
对于Training Set来说：Cost Function 平均平方误差（MSE）
穷举法：每一点都计算损失（实际中会先采样）
模型为 y = w * x 的代码：
import numpy as np
import matplotlib.pyplot as plt
# 相同的索引对应一组样本
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
# 定义模型
def forward(x):
return x * w
# 定义损失函数
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)*(y_pred-y)
# 把权重（多个）及其对应的损失值保存到列表里
w_list = []
mse_list = []
# np.arange(start, end, step) 创建数组
for w in np.arange(0.0,4.1,0.1): # 从0.0到4.0，每次间隔0.1
print('w=',w)
l_sum = 0
for x_val,y_val in zip(x_data,y_data): # zip()将两个列表的数据一对一对拼在一起
y_pred_val = forward(x_val)
loss_val = loss(x_val,y_val)
l_sum += loss_val # 没做均值
print('\t',x_val, y_val, y_pred_val, loss_val) # \t相当于一个tab键
print('MSE=',l_sum/3)
print('------------------------')
w_list.append(w)
mse_list.append(l_sum/3)
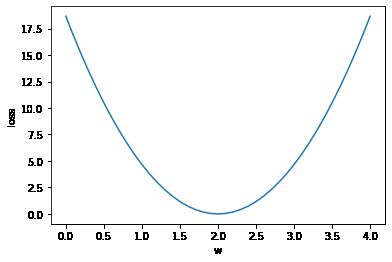
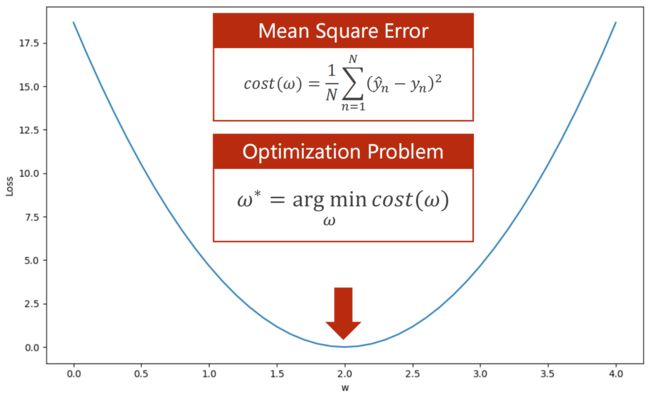
真实的深度学习训练过程难以判断什么时候收敛，超参数：确定模型是否训练成功了，收敛还是发散？
- 可视化
- 打印日志
训练过程中实时画图的工具：visdom库
详解PyTorch可视化工具visdom（一）_奋斗の博客-CSDN博客_visdom
plt.plot(w_list,mse_list)
plt.ylabel('loss')
plt.xlabel('w')
plt.show() 
一般拿训练轮数（epoch）做横轴
---------------------------------------------------------------------------------------------------------------------------------
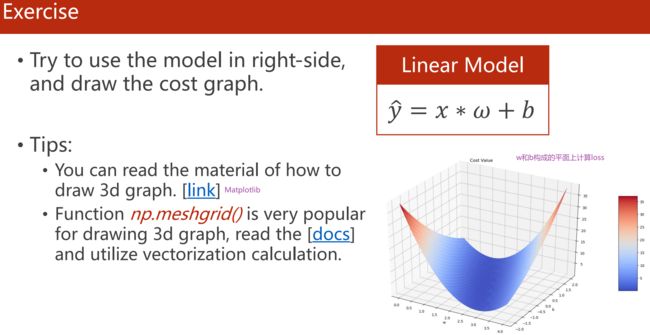
作业
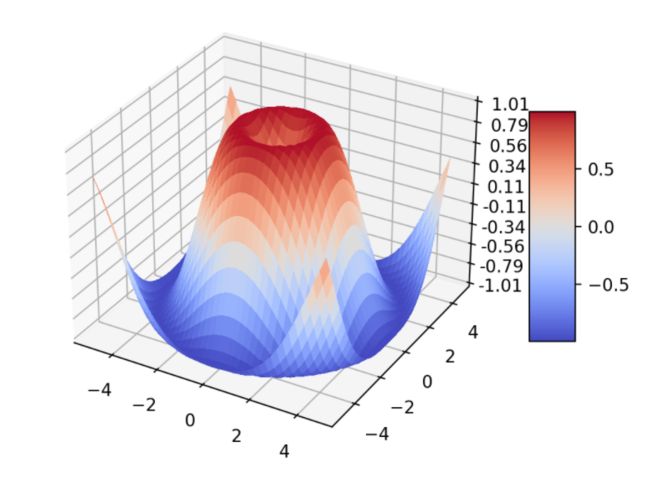
画3D图：
- Matplotlib： The mplot3d Toolkit — Matplotlib 3.5.1 documentation
- np.meshgrid()：numpy.meshgrid — NumPy v1.22 Manual
Matplotlib画3D图的示例代码：
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
# Make data.
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
# Plot the surface.
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# Customize the z axis.
ax.set_zlim(-1.01, 1.01)
ax.zaxis.set_major_locator(LinearLocator(10))
# A StrMethodFormatter is used automatically
ax.zaxis.set_major_formatter('{x:.02f}')
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
模型为 y = w * x + b 的代码：
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
import numpy as np
# Make data.
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 定义模型
def forward(x):
return x * w + b
# 定义损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# 定义空列表
w_list = []
b_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
for b in np.arange(-2.0, 2.1, 0.1):
print('w=',w,'b=',b)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print("MSE=", l_sum/3)
print('--------------------------------')
w_list.append(w)
b_list.append(b)
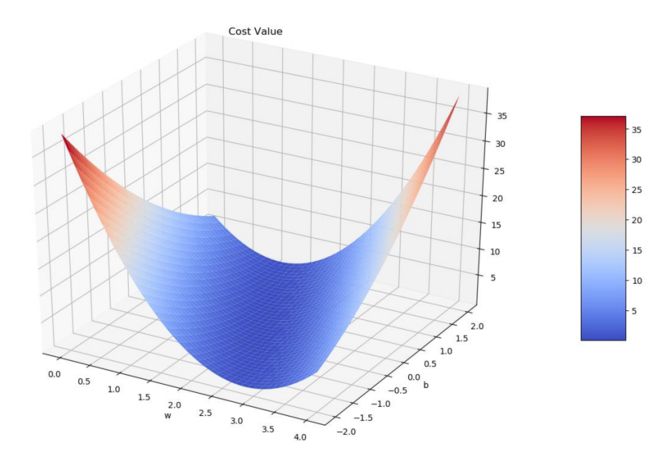
mse_list.append(l_sum/3)
画3D图的代码（接上）：
'''
此时得到的mse_list是一个列表
1、将其转化成矩阵（1681*1）
2、将其转化成41*41的矩阵（此时的w和b的值并不对应，即x axis与y axis反了）
3、故转置矩阵
'''
mse_list = np.array(mse_list) # 将列表转化成矩阵
mse_list = mse_list.reshape(41,41) # 将矩阵从1681*1变为41*41
mse_list = mse_list.transpose() # 转置矩阵
# w和b由于嵌套的for循环，每个值都出现了41次，故要去重，接下来使用meshgrid将w和b转化成41*41的矩阵
w, b = np.meshgrid(np.unique(w_list), np.unique(b_list))
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
# Plot the surface.
surf = ax.plot_surface(w, b, mse_list, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# Customize the z axis.
ax.set_zlim(0, 35)
ax.zaxis.set_major_locator(LinearLocator(10))
# A StrMethodFormatter is used automatically
ax.zaxis.set_major_formatter('{x:.00f}') # . 02f效果是z轴上的数字尺度保留两位小数
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
# 给每个轴标上含义
ax.set_xlabel('w')
ax.set_ylabel('b')
ax.text2D(0.4, 0.92, "Cost Values", transform=ax.transAxes)
plt.show()
3. Gradient Descent（梯度下降算法）
梯度下降：训练模型的一种方法
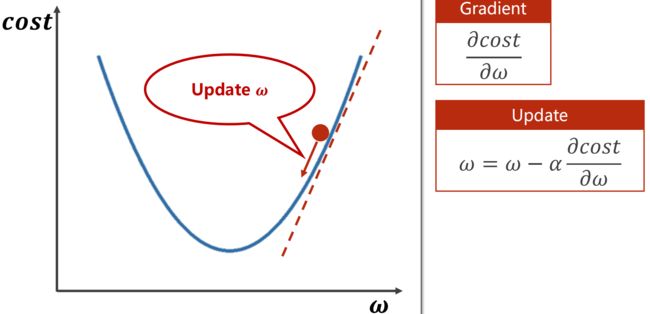
1、寻找最优w值的几种方法
- 穷举法：w在一个区间里一个一个的尝试，直到找到最小cost时的w值
- 分治法：曲线若为光滑的凸函数可用分治法，若为不规则曲面，很容易错过真正的最优点
- 梯度下降（贪心法）：只看眼前最好的选择，只能得到局部区域最好的结果，难以找到全局最优。梯度下降法中，负梯度方向是下降方向，也是往cost最小值走的方向
鞍点：梯度为0的点
2、梯度下降法（Gradient Descent Algorithm）
代码（训练前）：
# 准备训练集
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
# 设置一个初始权重（随机）
w = 3.0
# 定义模型
def forward(x):
return x*w
# 定义损失函数
def cost(xs,ys): # xs和ys是形参，代表着把x和y所有的数据都拿进来进行运算
cost = 0
for x,y in zip(xs,ys):
y_pred = forward(x)
cost += (y_pred - y)**2 # 平方
return cost/len(xs) # len(xs)为样本数量
# 定义梯度函数（即cost函数对权重w求偏导）
def gradient(xs,ys):
grad = 0
for x,y in zip(xs,ys):
grad += 2*x*(x*w-y)
return grad/len(xs)
print('Predict before training',4,forward(4)) # Predict before training 4 12.0代码（训练）：
epoch_list = []
cost_list = []
# 更新w
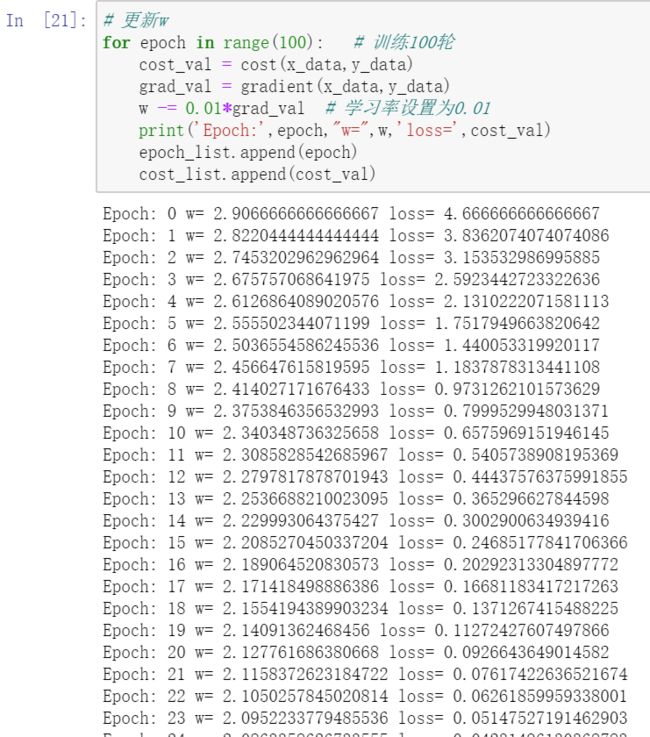
for epoch in range(100): # 训练100轮
cost_val = cost(x_data,y_data)
grad_val = gradient(x_data,y_data)
w -= 0.01*grad_val # 学习率设置为0.01
print('Epoch:',epoch,"w=",w,'loss=',cost_val)
epoch_list.append(epoch)
cost_list.append(cost_val)
print('Predict after training',4,forward(4)) # Predict after training 4 8.000222241378795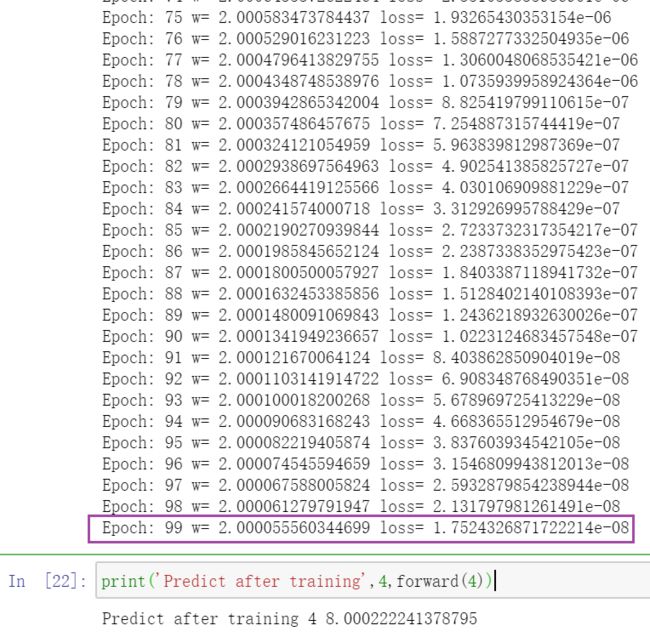
w趋于2，loss趋于0
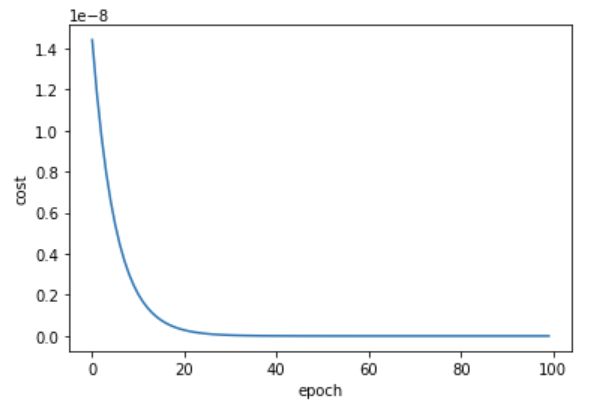
代码（画图）：
import matplotlib.pyplot as plt
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
注：cost是针对多个样本来说的，loss是针对一个样本来说的
--------------------------------------------------------------------------------------------------------------------------------
1、真实场景中，损失很难降到0，因为数据中是有噪声的，所以也不知道真正的最小值到底是多少，如何辨别？
绘图时可以做一个指数加权均值，使cost函数的图像变得更平滑，这样更容易观察整体的下降趋势
加权平滑公式：C0'=C0，Ci' = βCi + (1-β)Ci-1'，其中β为权重
其中：C0表示第0轮的损失，C1表示第1轮的损失... 更新后：C0'，C1'...
2、对于训练集来说，若训练时cost的图像下降后又上升了，说明训练发散了，无法收敛，训练失败了（而不是最小值的地方是cost最小）
训练失败的最常见原因是：学习率取大了
3、随机梯度下降法（Stochastic Gradient Descent Algorithm）
在神经网络中被证明十分有效
为什么使用随机梯度下降？
若所有样本算出来的损失函数图像里有鞍点，那么到鞍点处就无法继续下降了。若每次只算其中一个样本的损失函数，会引入随机噪声，这样即使陷入鞍点，随机噪声可能将我们向前推动，跨越鞍点，向最优值前进
代码：
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = 1.0
def forward(x):
return x*w
def loss(x,y):
y_pred = forward(x)
return (y_pred - y)**2
def gradient(x,y):
return 2*x*(x*w-y)
print('Predict before training',4,forward(4)) # Predict before training 4 4.0
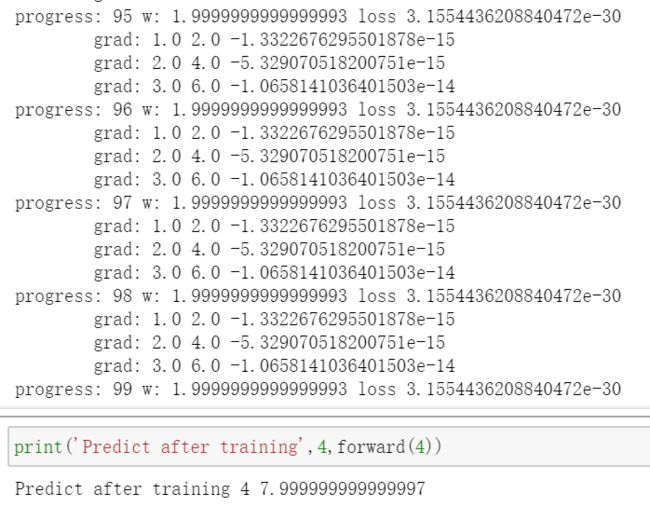
# 对每一个样本的梯度进行更新
for epoch in range(100):
for x,y in zip(x_data,y_data):
grad=gradient(x,y)
w -= 0.01*grad
print('\tgrad:',x,y,grad)
l = loss(x,y)
print("progress:",epoch,"w:",w,"loss",l)
print('Predict after training',4,forward(4)) # Predict after training 4 7.999999999999997 
用梯度下降计算梯度时，f(xi) 和 f(x i+1) 时是没有互相依赖关系的，即这些运算是可以并行的，但性能不如随机梯度下降；
但在随机梯度下降中，xi 的梯度要对w进行更新，下一个样本更新时的w是从上一个样本中拿过来的。即两个样本之间的梯度下降是不能并行化的，是有依赖的，时间复杂度高
即：梯度下降效率高，可以利用并行化运算的优势；随机梯度下降学习器性能更好，更容易找到最优点，但是运算性能低，无法利用并行性，时间复杂度高
在深度学习中，采用一种折中的方式：Mini-Batch 批量随机梯度下降。每次用若干个一组的样本去求相应的梯度，进行更新
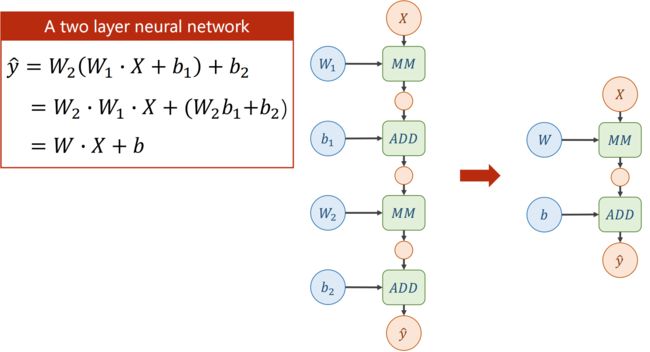
4. Back Propagation（反向传播）
反向传播：在图上进行梯度传播，是神经网络中非常重要的算法
线性模型可以看成一个非常简单的神经网络
把网络看成一个图，在图上传播梯度，最终根据链式法则求出梯度
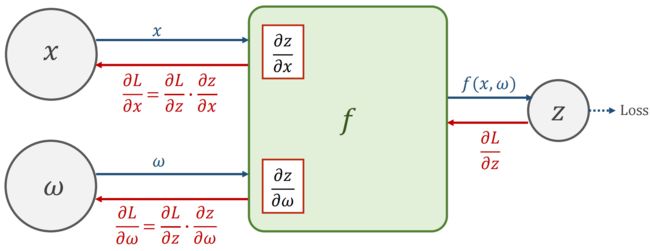
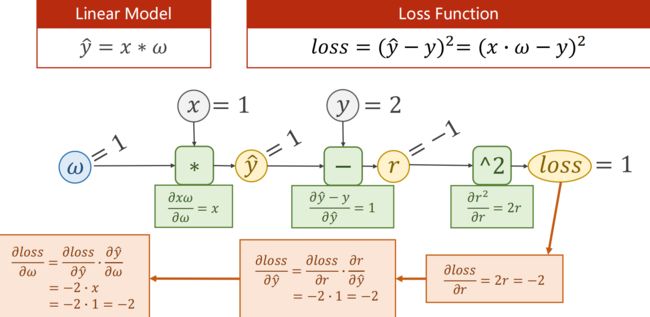
1、计算图
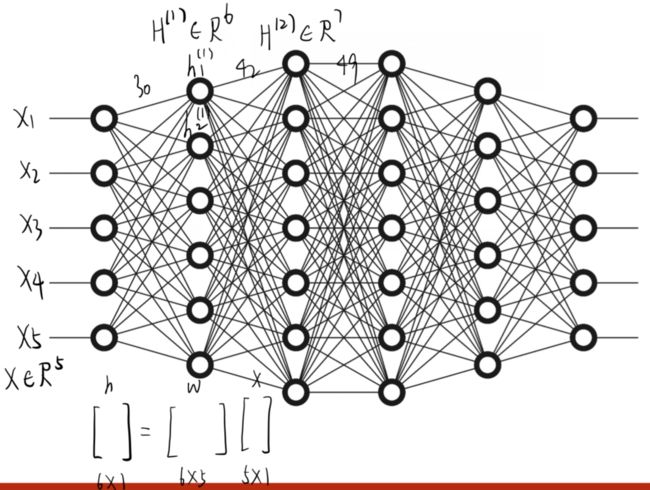
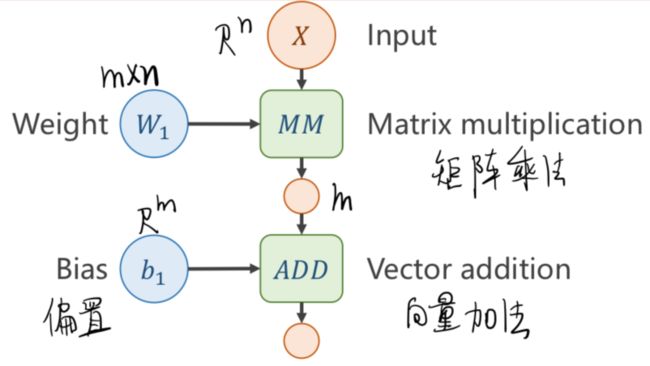全连接神经网络的第一层
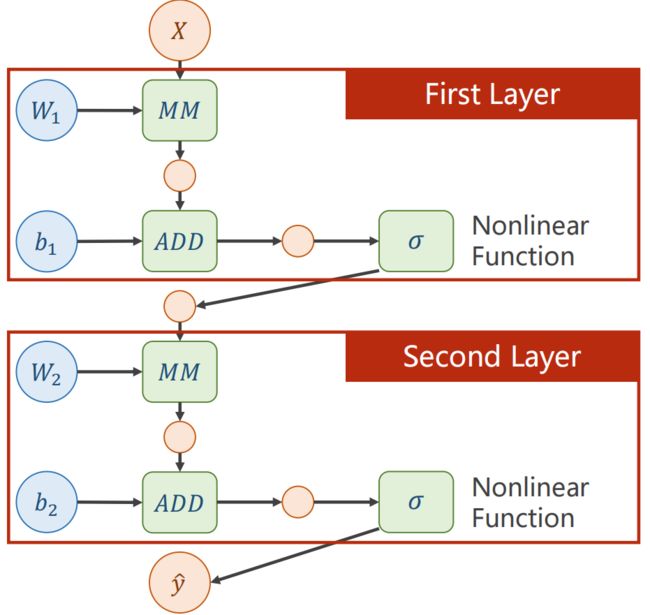
若不加激活函数，不管有多少层，最终都能统一成 wx+b 的形式，也就是说层数多少是没有区别的
所以，为了提高模型的复杂度，在每一层都要加非线性变换函数，如Sigmoid
链式法则：
得到相应导数后就可以做权重更新了
线性模型的计算图：
思路： 先forward，再backward，求梯度（更新）
保存loss，可视化，判断训练是否收敛
---------------------------------------------------------------------------------------------------------------------------------
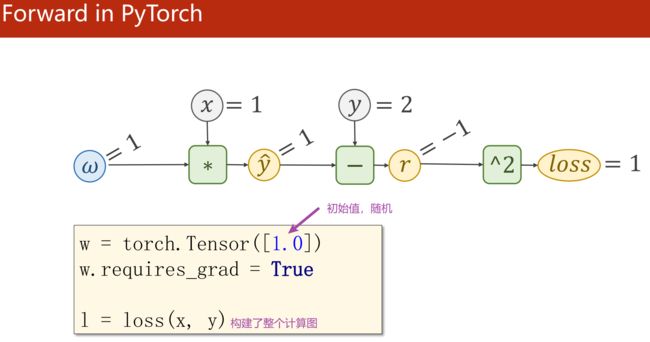
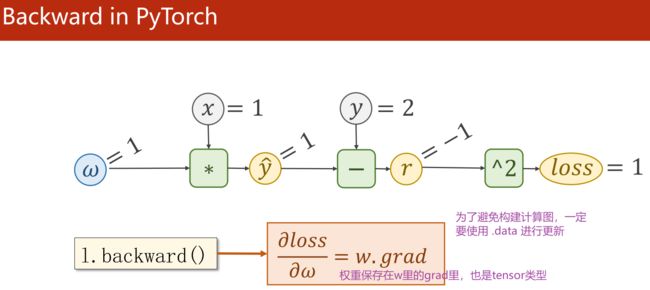
2、Tensor in PyTorch
Tensor 是 Pytorch 里的基本数据单元，可以存标量、向量、矩阵、高维度Tensor
一个 Tensor 包含权重值w（Data）和损失对权重的导数（Grad）
- 用 Tensor 计算就是在构建计算图
- w.grad.item() 把梯度里的数值直接拿出来变为标量
- w.grad.data 取张量的data，不会建立计算图，在权重更新时不使用张量
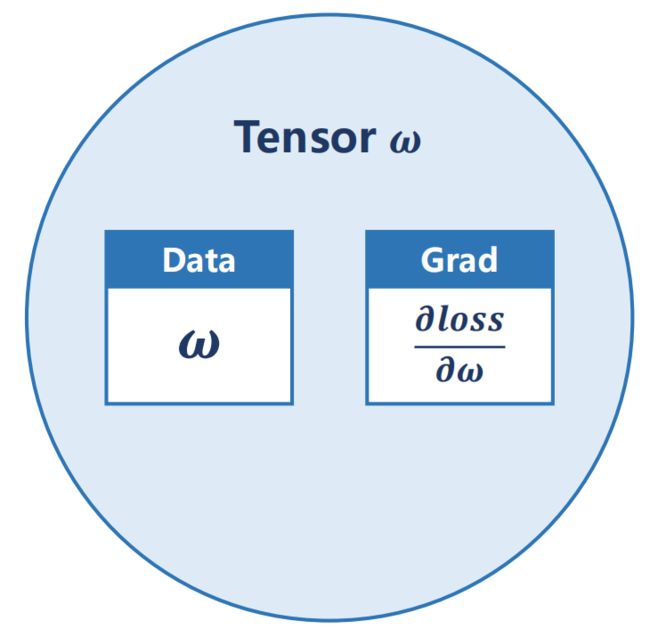Grad 也是 tensor 类型
用 Pytorch 实现线性模型：
代码：
import torch
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = torch.Tensor([1.0]) # 选择一个权重，创建一个Tensor变量，值为1.0
w.requires_grad = True # 需要计算梯度
def forward(x):
return x*w # w是tensor类型的，x会自动类型转换为tensor
def loss(x,y): # 每调用一次loss，就是在动态构建一次计算图
y_pred = forward(x)
return (y_pred-y)**2
print('predict before training',4,forward(4).item()) # predict before training 4 4.0
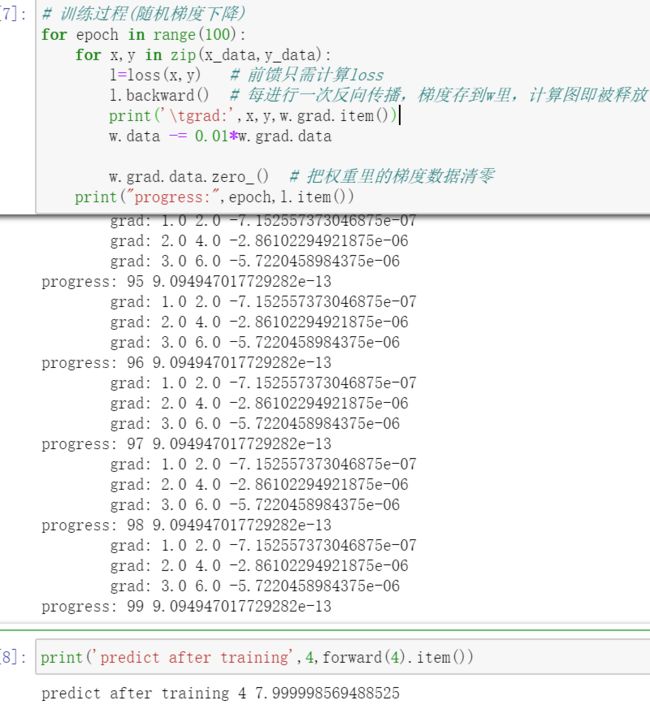
# 训练过程(随机梯度下降)
for epoch in range(100):
for x,y in zip(x_data,y_data):
l=loss(x,y) # 前馈只需计算loss
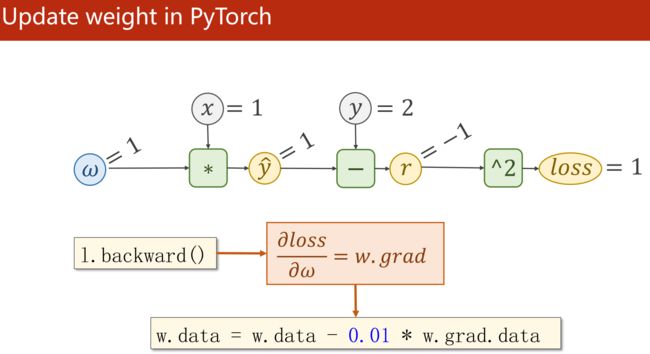
l.backward() # 每进行一次反向传播，梯度存到w里，计算图即被释放
print('\tgrad:',x,y,w.grad.item())
w.data -= 0.01*w.grad.data
w.grad.data.zero_() # 把权重里的梯度数据清零
print("progress:",epoch,l.item())
print('predict after training',4,forward(4).item()) # predict after training 4 7.999998569488525
若想累加损失，循环前加一句 sum=0，循环中加一句 sum += l.item()。因为张量做加法运算会构建计算图，l本身是张量tensor类型，所以要调用 .item()。否则，sum是关于l的计算图，非常吃内存，且又没在sum上进行backward，不需要构建计算图
5. Linear Regression with Pytorch（用Pytorch实现线性回归）
1、Before：线性模型如何训练、如何更新权重
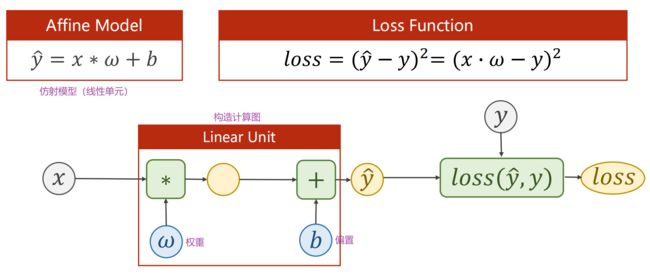
- 模型：线性模型
- 优化目标：损失函数（标量值）
随机梯度下降的核心：求出损失关于每一个权重的梯度，用随机梯度下降对权重进行更新
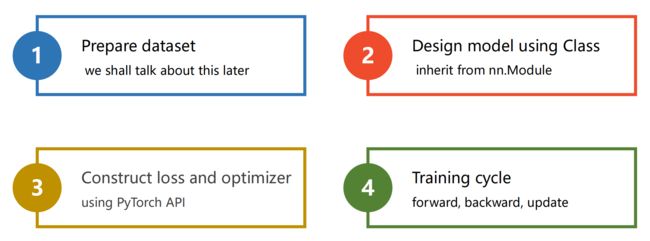
2、Now：如何构造神经网络 nn.Module、损失函数 loss、随机梯度下降的优化器
用Pytorch，代码有非常好的弹性，易扩展，易构造更复杂的神经网络
梯度下降训练：前馈算损失，反馈算梯度，更新权重
（1）Prepare dataset
x 和 y 的值必须为矩阵
（2）设计模型
知道 x 和 y_pred 的维度，就能确定 w 和 b 的维度
loss 必须是一个标量，因为对 loss 调用 backward，对整个计算图进行反向传播，而向量无法用 backward
设计模型时不用写 backward()，因为 Module 构造的对象会自动根据计算图实现 backward 的过程
要使对象可调用，要定义 __call__() 方法
（3）构造损失函数和优化器
最后一批 minibatch 数量不够时，可以求均值 1/N
优化器不会构建计算图
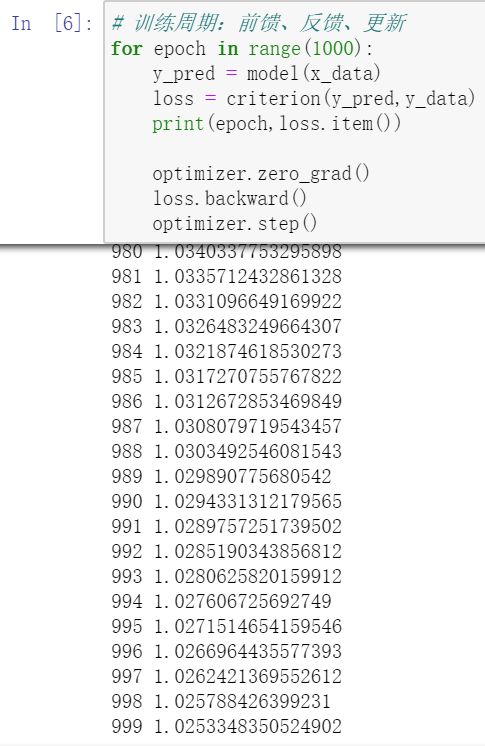
（4）训练周期
还未收敛则增加训练次数 epoch
前馈、反馈、更新
完整代码：
import torch
# step1
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])
# step2
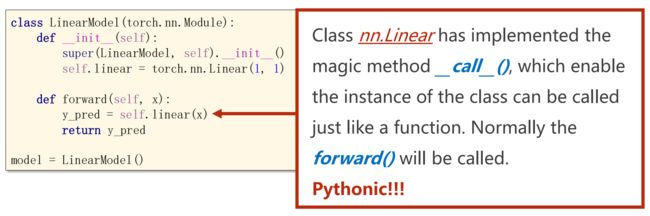
class LinearModel(torch.nn.Module): # LinearModel继承nn.Module这个父类
def __init__(self): # 构造函数（初始化对象时默认调用）
super(LinearModel,self).__init__() # 调用父类的构造
self.linear = torch.nn.Linear(1,1) # nn.Linear类，构造对象，包含权重w和偏置b两个tensor
def forward(self,x): # 前馈时要执行的计算
y_pred = self.linear(x)
return y_pred
model = LinearModel() # 实例化
# step3
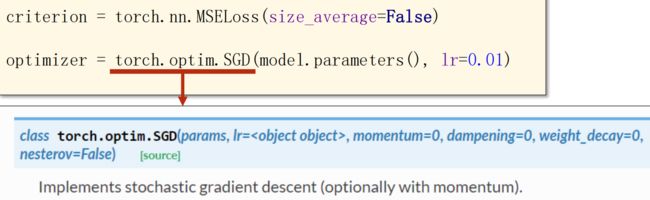
criterion = torch.nn.MSELoss(size_average=False) # nn.MSELoss继承自nn.Module
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
# step4
for epoch in range(1000):
y_pred = model(x_data) # 前馈：预测，算y_pred
loss = criterion(y_pred,y_data) # 前馈：损失，算loss
print(epoch,loss) # loss自动调用__str__()，不会产生计算图
optimizer.zero_grad() # 梯度归零
loss.backward() # 反向传播
optimizer.step() # 更新
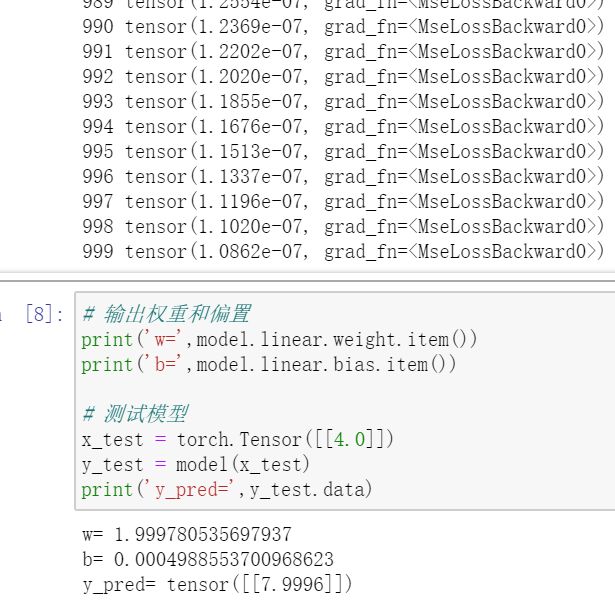
# 输出权重和偏置
print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())
# 测试模型
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred=',y_test.data)
--------------------------------------------------------------------------------------------------------------------------------
Exercise
1、尝试不同的优化器
2、资料
Learning PyTorch with Examples — PyTorch Tutorials 1.10.1+cu102 documentation
6. Logistic Regression（逻辑斯蒂回归）
逻辑回归（Logistic Regression）是机器学习任务的分类问题（y 属于离散集合）
对比：线性回归
线性回归中的 y 属于实数（连续空间）
loss 计算单个样本的损失
分类问题中的数据集：
（1）MNIST Dataset（手写数字的数据集）
非常基础的数据集，可以测量学习器的性能指标
类别：0-9 共 10 类
输出：属于每一类别的概率（十个类别的概率值相加为1），判断是哪个类，找最大的概率值即可。而不是直接输出 0-9 某一类别的数字，因为类别间并无实数空间中数值大小的含义
import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist',train=True,download=True)
test_set = torchvision.datasets.MNIST(root='../dataset/mnist',train=False,download=True)（2）CIFAR-10 Dataset（32x32的彩色图片，共10类）
---------------------------------------------------------------------------------------------------------------------------------
怎样从 R 映射到 [0,1]
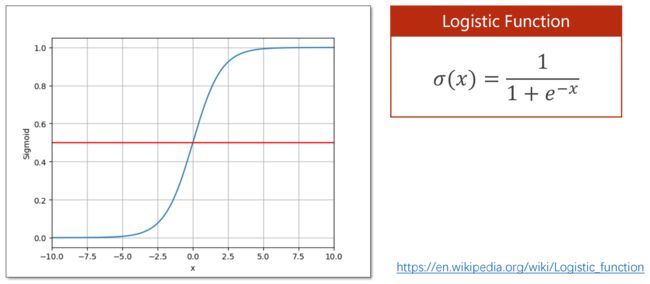饱合函数：超过某一阈值后，导数变得越来越小
https://en.wikipedia.org/wiki/Logistic_function
Sigmoid 函数：
满足3个条件：（1）函数值有极限（2）单调增（3）饱合函数
其中最出名的是 logistic 函数
---------------------------------------------------------------------------------------------------------------------------------
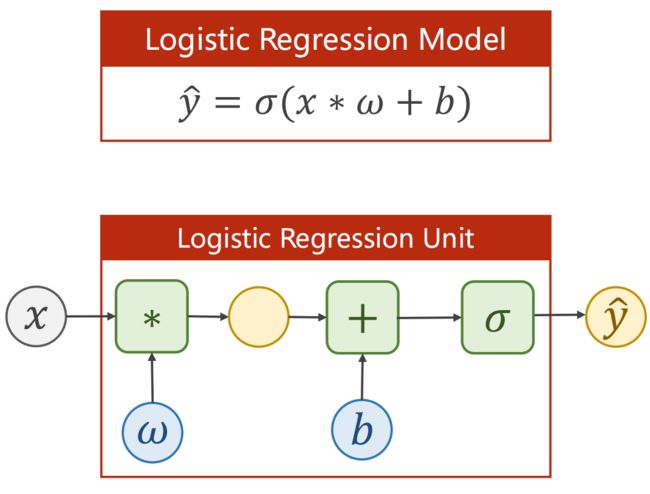
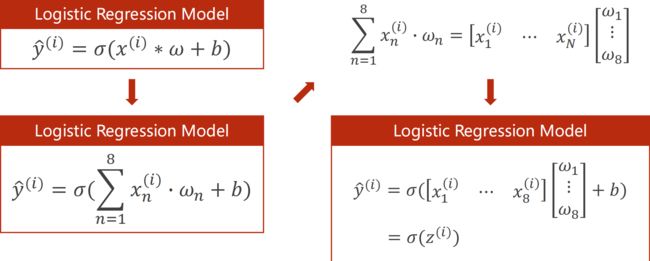
逻辑回归模型
能保证输出值在 [0,1] 之间
Logistic Function 无参数可供训练，不需在构造函数里初始化
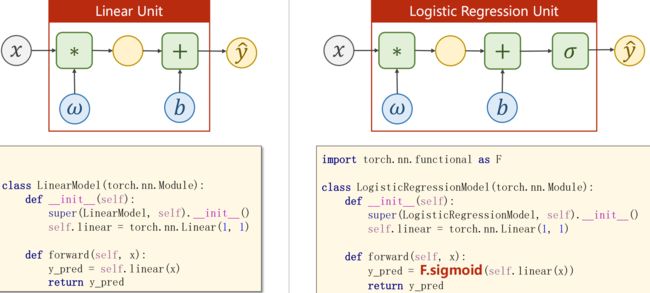
import torch.nn.functional as F
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel,self).__init__()
self.linear=torch.nn.Linear(1,1)
def forward(self,x):
y_pred=F.sigmoid(self.linear(x))
return y_pred---------------------------------------------------------------------------------------------------------------------------------
损失函数（Binary Cross Entropy，二分类交叉熵）
求均值
criterion = torch.nn.BCELoss(size_average=False)size_average 参数：是否给每一批量求均值，影响将来如何选择学习率
另：比较两个分布的差异的参数有
- KL散度
- Cross Entropy（交叉熵）：
---------------------------------------------------------------------------------------------------------------------------------
逻辑回归的完整代码
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
# 准备数据集
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]])
# 设计模型（从nn.Module继承）
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel,self).__init__()
self.linear=torch.nn.Linear(1,1)
def forward(self,x):
y_pred=F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
# 构造损失函数和优化器（使用Pytorch API）
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
# 训练周期：前馈、反馈、更新
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
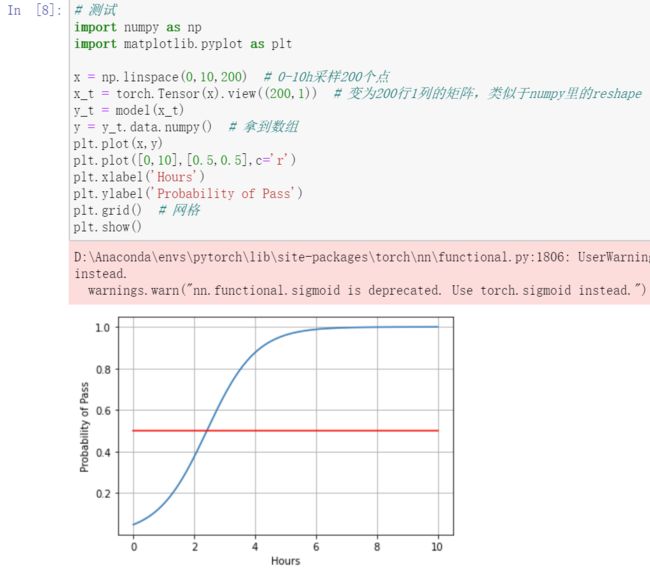
# 测试
x = np.linspace(0,10,200) # 0-10h采样200个点
x_t = torch.Tensor(x).view((200,1)) # 变为200行1列的矩阵，类似于numpy里的reshape
y_t = model(x_t)
y = y_t.data.numpy() # 拿到数组
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid() # 网格
plt.show() 
7. Multiple Dimension Input（处理多维特征的输入）
多维输入：x有很多特征，预测一条样本的对应分类
糖尿病数据集（Diabetes Dataset）：
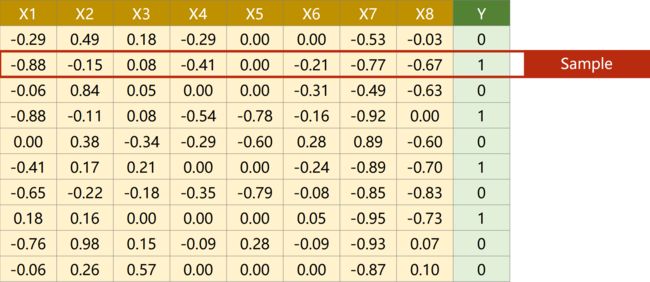样本 
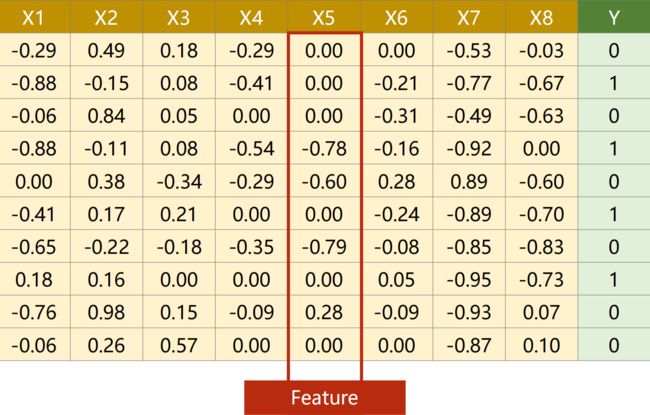特征/字段
Mini-Batch（N个样本）
PyTorch 提供的函数都是向量化函数
Sigmoid 函数是按向量计算，依次运用到每个元素上
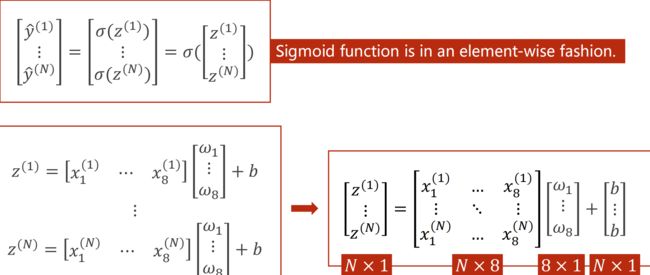一组方程的运算 合并为 矩阵运算/向量化运算（并行计算能力）
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
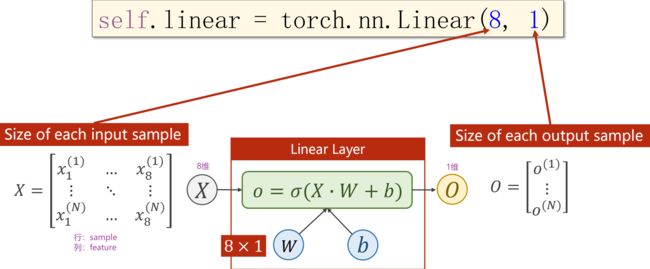
self.linear = torch.nn.Linear(8,1) # 输入维度是8，输出维度是1
self.sigmoid = torch.nn.Sigmoid()
def forward(self,x):
x = self.sigmoid(self.linear(x))
return x
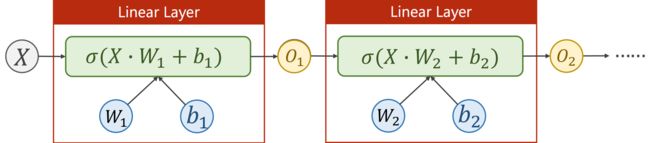
model = Model()线性层（空间维度的变换）：
矩阵是一个空间变换的函数，把8维空间的向量映射到1维空间（线性映射）
映射不一定是线性的，用多个线性变换层，通过找到最优的权重，把它们组合起来，模拟非线性变换。神经网络的本质是寻找非线性空间的变换函数
激活函数：给线性变换增加非线性因子，从而拟合非线性变换
神经网络：
从 X 到 O1 到 O2 ... ，维度可以逐步下降，也可以先上升再下降
到底几层，每一层维度设为多少？ —— 超参数的搜索的方法进行尝试
隐层越多，非线性变换的学习能力就越强，但学习能力过强也不好，会把输入样本里噪声的规律也学到，但我们要学的是数据真值本身的规律（模型必须要有泛化能力）
人工神经网络：
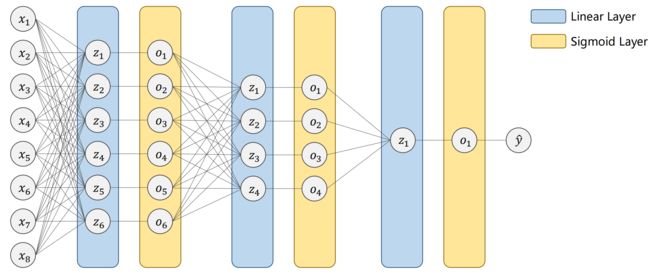
例子：糖尿病预测
- X：8个维度，为糖尿病病人的一些指标
- Y：0或1，为一年后病情是否会加重
完整代码：
# 准备数据集
import torch
import numpy as np
xy = np.loadtxt('diabetes.csv.gz',delimiter=',',dtype=np.float32) # delimiter为分隔符
# torch.from_numpy()创建Tensor
x_data = torch.from_numpy(xy[:,:-1]) # 所有行，第1列开始，最后1列不要
y_data = torch.from_numpy(xy[:,[-1]]) # -1外面加[]是为了保证拿出来是一个矩阵，不加的话拿出来是一个向量
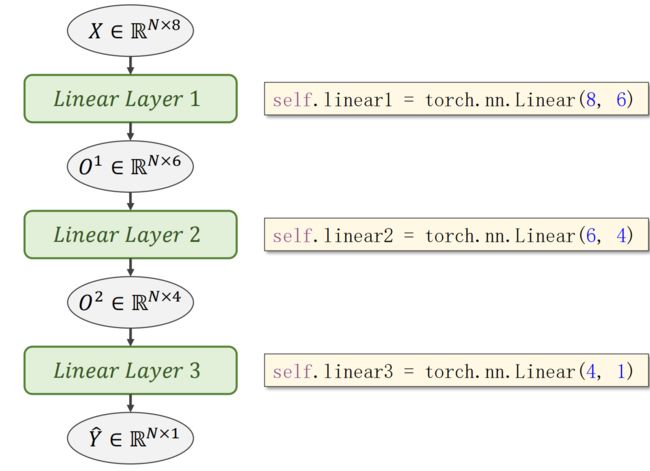
# 定义模型（输入8维—>线性层1—>6维—>线性层2—>4维—>线性层3—>输出1维）
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = torch.nn.Linear(8,6)
self.linear2 = torch.nn.Linear(6,4)
self.linear3 = torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid() # 给模型添加一个非线性变换，继承自Module；另一种写法：torch.nn.Functional.Sigmoid()
def forward(self,x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
# 构建损失和优化器
criterion = torch.nn.BCELoss(size_average=True) # loss取平均值变小了，学习率最好调大一点
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)
# 训练周期（训练时尚未使用Mini-Batch）
for epoch in range(100):
# 前馈
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss.item())
# 反馈
optimizer.zero_grad()
loss.backward()
# 更新
optimizer.step()
Exercise：
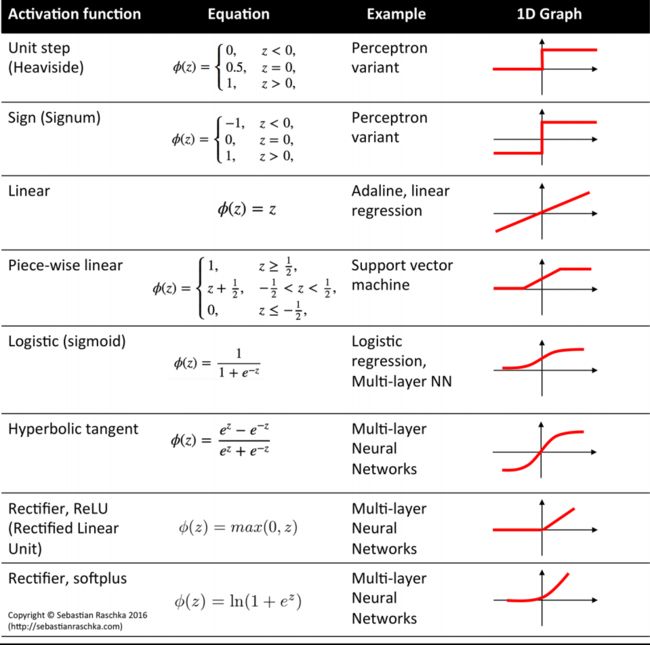
尝试不同的激活函数
Visualising Activation Functions in Neural Networks - dashee87.github.io
Activation Functions for Artificial Neural Networks - mlxtend
Pytorch提供了大量的激活函数
torch.nn — PyTorch 1.10 documentation
如将激活函数换成 ReLU 时的代码：
import torch
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear = torch.nn.Linear(8,6)
self.linear = torch.nn.Linear(6,4)
self.linear = torch.nn.Linear(4,1)
self.activate = torch.nn.ReLU()
def forward(self,x):
x = self.activate(self.linear1(x))
x = self.activate(self.linear2(x))
x = self.activate(self.linear3(x))
return x
model = Model()8. Dataset and Dataloader（加载数据集）
加载数据的两个工具集：
- Dataset：构造数据集（支持索引：用下标可以拿出数据集中的样本）
- Dataloader：拿出一组 Mini-Batch 供训练
1、梯度下降：全部数据都用（Batch）
- 最大化利用向量计算的优势，来提升计算速度
- 但性能会遇到问题
2、随机梯度下降（SGD）：只用一个样本
- 得到较好的随机性，跨越优化中遇到的鞍点，性能更好
- 但导致优化时间过长，无法利用GPU或CPU的并行能力
3、深度学习（DL）：Mini-Batch
- 均衡性能上及训练时间上平衡的需求
---------------------------------------------------------------------------------------------------------------------------------
区分 Epoch Batch-Size Iteration
Epoch：所有训练样本经历了一次前向传播和反向传播的过程（嵌套循环）
Batch-Size：每次训练时用的样本数量
Iteration：Batch分了多少个迭代次数
# training cycle
for epoch in range(training_epochs): # 训练周期
# Loop over all batches
for i in range(total_batch): # Mini-batch，对Batch进行迭代---------------------------------------------------------------------------------------------------------------------------------
Dataset：提供索引和 len()
DataLoader：batch_size=2，shuffle=True
为了提高训练数据样本的随机性，可对数据集进行 shuffle（打乱），打乱的是每一次 epoch 拿到的数据
---------------------------------------------------------------------------------------------------------------------------------
如何定义数据集
构造数据集时：
- 从 init 里读取所有数据，加载到内存；使用 getitem，传出第 [i] 个样本
适用于数据集容量不大的情况，如结构化数据表 - 在 init 里定义列表，储存数据集里每一个文件的文件名、标签（或标签的文件名），getitem 读取列表中的第 [i] 个元素
适用于如图像、语音等非结构化数据，或无法一次性加载到内存中的情况
import torch
from torch.utils.data import Dataset # Dataset是一个抽象类，不能实例化，只能被其他子类继承
from torch.utils.data import DataLoader # DataLoader类（加载器）可以实例，加载数据（shuffle和batch_size自动完成）
class DiabetesDataset(Dataset): # DiabetesDataset是自己定义的类，继承自Dataset类
def __init__(self):
pass
def __getitem__(self,index): # 实例化对象后支持下标操作，通过索引拿出数据
pass
def __len__(self): # 返回数据集里的数据条数，即整个数据的数量
pass
dataset = DiabetesDataset() # 实例化为数据对象
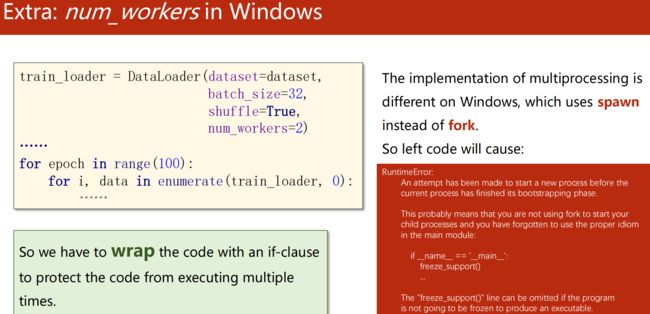
# DataLoader初始化时至少传4个量，num_workers：读数据、构成Mini-Batch时是否多线程（并行化），并行化可提高读取的效率
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)Windows 下 num_workers 会报错，因为 Linux（fork）和 win（spawn）实现多进程的库不一样
解决：把 loader 要进行迭代的代码封装起来（ if 语句或函数）
例子：糖尿病数据集（Diabetes Dataset）
使用神经网络对糖尿病数据集进行分类
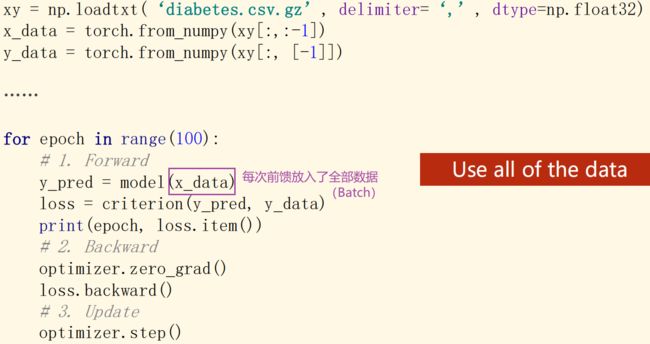
当使用 Mini-Batch 而不是一次性加载 All Data 时，“step1 准备数据集” 和 “step4 训练周期” 改变
import numpy as np
import torch
from torch.utils.data import Dataset,DataLoader
# 1、准备数据（不再是加载全部数据）
class DiabetesDataset(Dataset):
def __init__(self,filepath):
xy = np.loadtxt(filepath,delimiter=',',dtype=np.float32)
self.len = xy.shape[0] # xy为N行9列（N行：数据样本个数；9列：8个特征列，1个目标列）
self.x_data = torch.from_numpy(xy[:,:-1]) # 前8列
self.y_data = torch.from_numpy(xy[:,[-1]]) # 最后1列
def __getitem__(self,index):
return self.x_data[index],self.y_data[index] # 返回的是一个元组
def __len__(self):
return self.len
dataset = DiabetesDataset('diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=0)
# 2、设计模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = torch.nn.Linear(8,6)
self.linear2 = torch.nn.Linear(6,4)
self.linear3 = torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self,x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
# 3、构建损失和优化器
criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
# 4、训练周期（变为了嵌套循环，以便使用Mini-Batch）
# 嵌套循环
for epoch in range(100):
# enumerate()获得当前是第几次迭代
for i,data in enumerate(train_loader,0): # data为元组(x,y)
# 1. 准备数据
inputs,labels = data
# 2. 前馈
y_pred = model(inputs)
loss = criterion(y_pred,labels)
print(epoch,i,loss.item())
# 3. 反馈
optimizer.zero_grad()
loss.backward()
# 4. 更新
optimizer.step()
--------------------------------------------------------------------------------------------------------------------------------
torchvision.datasets
例子：MNIST Dataset
import torch
from torch.utils.data import DataLoader
from torchvision import transforms # PIL Image —> Tensor
from torchvision import datasets
train_dataset = datasets.MNIST(root='../dataset/mnist',train=True,transform=transform.ToTensor(),download=True)
test_dataset = datasets.MNIST(root='../dataset/mnist',train=False,transform=transform.ToTensor(),download=True)
train_loader = DataLoader(dataset=train_dataset,batch_size=32,shuffle=True)
test_loader = DataLoader(dataset=test_dataset,batch_size=32,shuffle=False) # 测试数据一般不需要shuffle
for epoch in range(100):
for batch_idx,(inputs,target) in enumerate(train_loader):
...---------------------------------------------------------------------------------------------------------------------------------
Exercise
- Build DataLoader for Titanic dataset：Titanic - Machine Learning from Disaster | Kaggle
- Build a Classifier using the DataLoader，目标：判断这名乘客是否活下来了
9. Softmax Classifier（多分类问题）
softmax：多分类
回顾：
- 糖尿病数据集（Diabetes Dataset）：二分类网络
- MNIST Dataset（测试方法是否有效的标准数据集）：10分类（0-9）
手写数字识别，每个图片为 28 * 28 = 784 个像素，每个像素取值为 0-255
--------------------------------------------------------------------------------------------------------------------------------
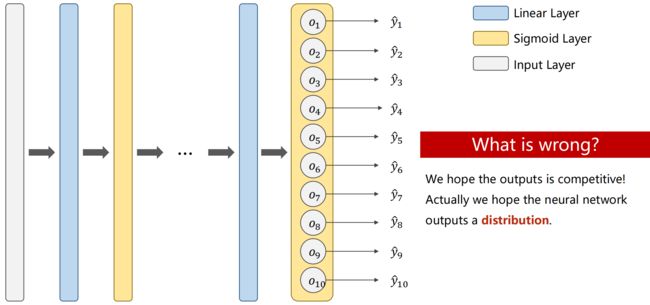
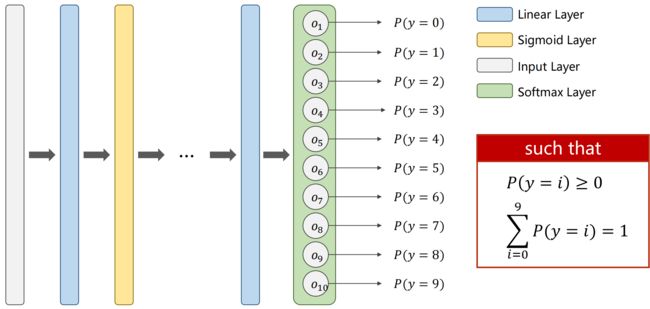
十分类问题神经网络应该怎么设计？
思路1：使用 Sigmoid 设计 10 输出，即输出每一个样本属于每一个分类的概率（把每一类别看成二分类问题，对每个输出应用二分类的 BCELoss 公式）
然而我们希望输出是有竞争性的（各个类别间应相互抑制），即输出满足分布的性质要求（输出都需 ≥0，且和为1）
思路2：最后一层为 softmax层，能够输出一个分布
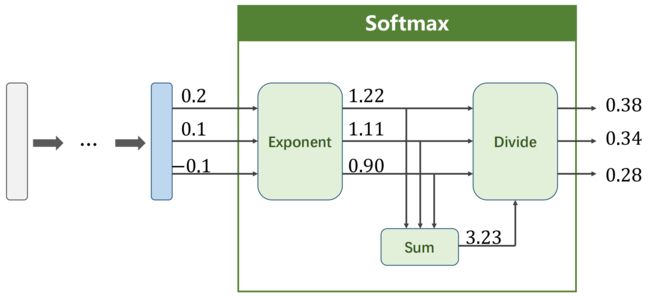
softmax 层：神经网络线性层的输出可能是负的，如何变为正值？如何和为1？
例：
Loss Function - Cross Entropy
- Cross Entropy in Numpy
import numpy as np y = np.array([1,0,0]) # Y数组 z = np.array([0.2,0.1,-0.1]) y_pred = np.exp(z)/np.exp(z).sum() # softmax：先求指数，再除以这些指数项的和 loss = (-y * np.log(y_pred)).sum() print(loss) # 0.9729189131256584 - Cross Entropy in PyTorch
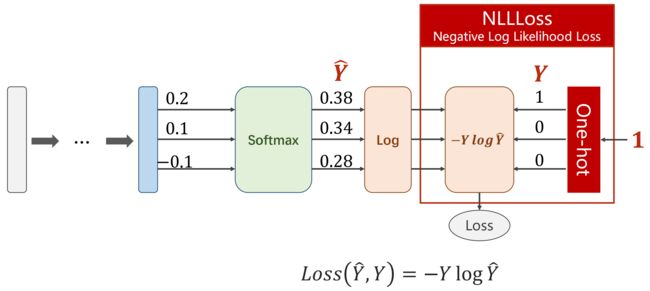
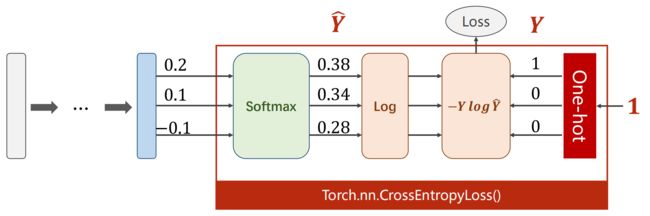
最后一层不用做非线性变换，直接用交叉熵损失（ torch.nn.CrossEntropyLoss() ）
import torch y = torch.LongTensor([0]) # 长整型张量 z = torch.Tensor([[0.2,0.1,-0.1]]) criterion = torch.nn.CrossEntropyLoss() loss = criterion(z,y) print(loss) # tensor(0.9729)
对比：CrossEntropyLoss（交叉熵损失） 和 NLLLoss（NLL损失）
CrossEntropyLoss 等价于 LogSoftmax + NLLLoss
- CrossEntropyLoss：torch.nn — PyTorch 1.10 documentation
- NLLLoss：torch.nn — PyTorch 1.10 documentation
Mini-Batch
batch_size=3
import torch
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2,0,1]) # 第几个标签分类
Y_pred1 = torch.Tensor([[0.1,0.2,0.9], # 2
[1.1,0.1,0.2], # 0
[0.2,2.1,0.1]]) # 1
Y_pred2 = torch.Tensor([[0.8,0.2,0.3], # 0
[0.2,0.3,0.5], # 2
[0.2,0.2,0.5]]) # 2
l1 = criterion(Y_pred1,Y) # Batch Loss1= tensor(0.4966)
l2 = criterion(Y_pred2,Y) # Batch Loss2= tensor(1.2389)
print("Batch Loss1=",l1.data,"\nBatch Loss2=",l2.data)
---------------------------------------------------------------------------------------------------------------------------------
对 MNIST 数据集构建分类器
部分代码解释：
1. Prepare dataset
transforms.ToTensor()
通道×宽×高
- 灰度图：单通道
- 彩色图：多通道（channel，C）
transforms.Normalize((0.1307, ),(0.3081, ))
整个 MNIST 数据集的均值和标准差分别为 0.1307 和 0.3081（经验数据）
2. Design Model
全连接神经网络要求输入为矩阵，所以 x.view(-1,784)，其中 view() 包含两个参数，即代表二阶张量（矩阵），784为矩阵列数（一张图片里的像素数量），-1代表 pytorch 自动计算其行数
3. Construct Loss and Optimizer
SGD 中有个参数 momentum（冲量），有助于突破局部极小值
4. Train
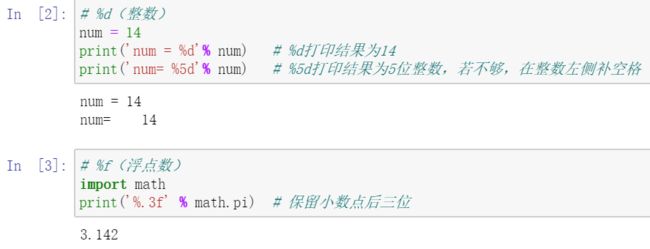
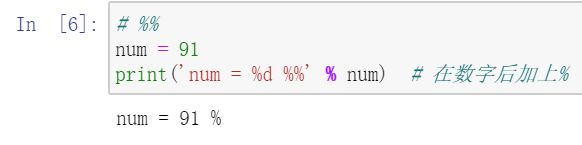
print('[%d,%5d]loss: %.3f' % (epoch+1,batch_idx+1,running_loss/300))print 格式化输出
5. Test
测试不需反向传播，只要正向
完整代码：
# 0.导包
import torch
from torchvision import transforms # 对图像进行原始处理的工具
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F # 为了使用函数 relu()
import torch.optim as optim # 为了构建优化器
# 1.准备数据
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), # PIL Image 转换为 Tensor
transforms.Normalize((0.1307, ),(0.3081, ))]) # 归一化到0-1分布，其中mean=0.1307，std=0.3081
train_dataset = datasets.MNIST(root='../dataset/mnist',train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,shuffle=True,batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist',train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,shuffle=False,batch_size=batch_size)
# 2.设计模型
class Net(torch.nn.Module):
def __init__(self):
super(Net,self).__init__()
# 线性层
self.l1 = torch.nn.Linear(784,512)
self.l2 = torch.nn.Linear(512,256)
self.l3 = torch.nn.Linear(256,128)
self.l4 = torch.nn.Linear(128,64)
self.l5 = torch.nn.Linear(64,10)
def forward(self,x):
x = x.view(-1,784)
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做激活，直接接到softmax
model = Net()
# 3.构建损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(),lr=0.01,momentum=0.5)
# 4.训练
def train(epoch): # 把一轮循环封装到函数里
running_loss = 0
for batch_idx, data in enumerate(train_loader,0):
inputs,target=data
optimizer.zero_grad()
# 前馈 反馈 更新
outputs = model(inputs)
loss = criterion(outputs,target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299: # 每300批量输出一次
print('[%d,%5d]loss: %.3f' % (epoch+1,batch_idx+1,running_loss/300))
running_loss = 0
# 5.测试
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images,labels = data
outputs = model(images)
_,predicted = torch.max(outputs.data,dim=1) # 求每一行里max的下标，对应着分类，其中dim=1为行，dim=0为列
total += labels.size(0) # (N,1)，取N
correct += (predicted==labels).sum().item()
print('Accuracy on test set: %d %%' %(100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test() # 训练一轮，测试一轮
# 若想每训练10轮测试1次，可在test()前面加一行 if epoch % 10 == 9: 
准确率到 97% 基本为极限了，因为：处理图像用全连接神经网络，忽略了对局部信息的利用（所有元素间都做全连接，权重不够多，且处理图像时更关心高抽象级别的特征，而现在只用了非常原始的特征）。若先特征提取再分类训练，效果会更好
图像人工提取特征的方法：
- 整张图像的特征提取：傅里叶变换（缺陷：都是正弦波，周期性）
- Wavelet 小波
自动提取特征的方法：CNN等
--------------------------------------------------------------------------------------------------------------------------------
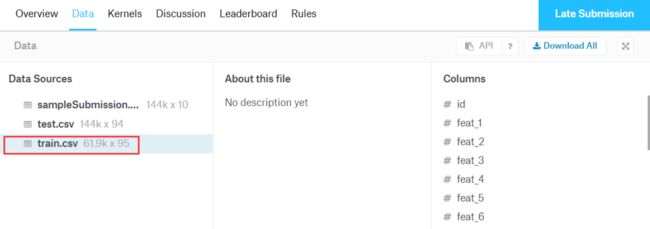
Exercise
奥托集团的产品分类挑战（多分类问题）
Otto Group Product Classification Challenge | Kaggle
