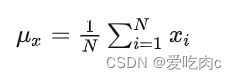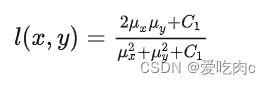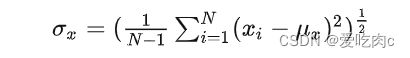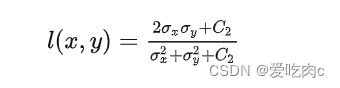图像去雾算法评价指标

---

前言

评价一个去雾算法的好坏，常常使用主观评价法和客观评价法。

---

一、主观评价

主观评价即通过肉眼观察经过去雾处理的图像，从图像的纹理特征、对比度、饱和度及细节信息等多方面进行感官感受和评价。主观评价主要是通过人眼视觉系统的主观感受在确定好的评价基础上做出相应的判断。这种方法的优点是不需要专业的技术或经验,且非常适合于色彩变化较大的图像;但也存在不足,例如不同的测试员对相同的处理结果极易出现偏差。

二、客观评价

1.PSNR

PSNR是“Peak Signal to Noise Ratio”的缩写，即峰值信噪比。
PSNR的单位是dB，数值越大表示失真越小。n为每像素的比特数，一般的灰度图像取8，即像素灰阶数为256.

MSE
用 真实值-预测值 然后平方之后求和平均。

在图像中的MSE定义说人话就是：

两个图像中每一个相同位置的像素值相减，平方，求和，再求平均。

表达的是两幅图在每一个位置上的像素值的差异的平均。

数值越大，表示两张图片在相似度上更低。

这里注意两点：

在计算之前要把两个图像调整为同一个阈值，一个[0,1]和一个[0,255]是不能放一起用的。
图像的大小要保持一致。不然无法做到像素值之间的一一对应。
MSE在描述两图像的相似成都时具有它的局限性。
其中一点是这个定义太简单了，不一定完全符合视觉上规律。
比如说如果两图像是少量的平移或者缩放关系，我们在视觉上的感受是两者之间并无太大差异，图像信息可能被完整地保留了下来（比如大头照）。但是他们计算MSE的时候会有一个不太理想的结果。

1.PSnr python代码实现

注意：若像素为0-1 则MAX=1 若像素为0-255 则MAX为255

import numpy as np
import math
import cv2

def PSNR(x, y):
    # x=np.float32(x/255.0)
    # y= np.float32(y / 255.0)
    MSE = np.mean((x/255.0 - y/255.0)**2)
    if MSE<1.0e-10:
        return 100
    MAX=1
    return 20 * math.log10(MAX / math.sqrt(MSE))

src=cv2.imread("image/wu5.jpg")
det=cv2.imread("image/wu30.jpg")
a=PSNR(src,det)
print(a)

np.mean() 函数定义：
numpy.mean(a, axis, dtype, out，keepdims)

mean()函数功能：求取均值
经常操作的参数为axis，以m * n矩阵举例：

axis 不设置值，对 mn 个数求均值，返回一个实数
axis = 0：压缩行，对各列求均值，返回 1 n 矩阵
axis = 1：压缩列，对各行求均值，返回 m *1 矩阵

2、SSIM(Structure Similarity Index Measure) 结构衡量指标

结构相似指标可以衡量图片的失真程度，也可以衡量两张图片的相似程度。与MSE和PSNR衡量绝对误差不同，SSIM是感知模型，即更符合人眼的直观感受。
SSIM的取值范围[-1, 1], 具有对成性，边界性，唯一最大性（当且仅当x=y时SSIM=1），是一种距离公式。

SSIM理论
SSIM 主要考量图片的三个关键特征：亮度（Luminance）, 对比度（Contrast）, 结构 (Structure)

1、Luminance

亮度以平均灰度衡量，通过平均所有像素的值得到。

对比函数

2、Contrast

对比度通过灰度标准差来衡量。标准差无偏估计：

相应对比函数

3、Structure

结构对比比较的是经过归一化后 与 的​​​​比较, 即可以用相关性系数衡量

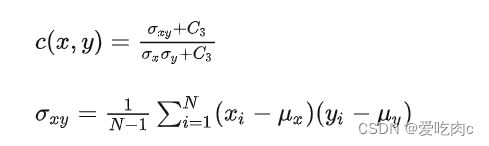
在这里插入图片描述

4、ssim

SSIM是衡量两幅图像相似度的指标，其取值范围为[0,1]，SSIM的值越大，表示图像失真程度越小，说明图像质量越好。

5、python代码实现：

import numpy as np
from PIL import Image
from scipy.signal import convolve2d

def gauss2D(shape=(3, 3), sigma=0.5):

    m, n = [(ss - 1.) / 2. for ss in shape]
    y, x = np.ogrid[-m:m + 1, -n:n + 1]
    h = np.exp(-(x * x + y * y) / (2. * sigma * sigma))
    h[h < np.finfo(h.dtype).eps * h.max()] = 0
    h_sum = h.sum()
    if h_sum != 0:
        h /= h_sum
    return h

def filter2(x, kernel, mode='same'):
    return convolve2d(x, np.rot90(kernel, 2), mode=mode)

def compute_ssim(image1, image2, k1=0.01, k2=0.03, win_size=11, L=255):

    if not image1.shape == image2.shape:
        raise ValueError("输入的两张图片大小应该一样")
    if len(image1.shape) > 2:
        raise ValueError("输入的图片应为灰度图")

    M, N = image1.shape
    C1 = (k1 * L) ** 2
    C2 = (k2 * L) ** 2
    window = gauss2D(shape=(win_size, win_size), sigma=1.5)
    window = window / np.sum(np.sum(window))

    if image1.dtype == np.uint8:
        image1 = np.double(image1)
    if image2.dtype == np.uint8:
        image2 = np.double(image2)

    mu1 = filter2(image1, window, 'valid')
    mu2 = filter2(image2, window, 'valid')
    mu1_sq = mu1 * mu1
    mu2_sq = mu2 * mu2
    mu1_mu2 = mu1 * mu2
    sigma1_sq = filter2(image1 * image1, window, 'valid') - mu1_sq
    sigma2_sq = filter2(image2 * image2, window, 'valid') - mu2_sq
    sigmal2 = filter2(image1 * image2, window, 'valid') - mu1_mu2

    ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigmal2 + C2)) / ((mu1_sq + mu2_sq + C1) * (sigma1_sq + sigma2_sq + C2))

    return np.mean(np.mean(ssim_map))

src=cv2.imread("image/wu5.jpg")
det=cv2.imread("image/wu32.jpg")
#一定要传入灰度图
srcgray=cv2.cvtColor(src,cv2.COLOR_BGR2GRAY)
detgray=cv2.cvtColor(det,cv2.COLOR_BGR2GRAY)
a=PSNR(src,det)
b=compute_ssim(srcgray,detgray)

3、MSE

1.基本概念

MSE全称为“Mean Square Error”，中文意思即为均方误差，是衡量图像质量的指标之一。计算原理为真实值与预测值的差值的平方然后求和再平均，公式如下：

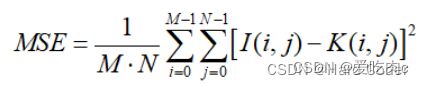
其中， M为图像I的像素总数，N为图像K的像素总数。MSE值越小，说明图像越相似

1.python中实现 有相应的api

src=cv2.imread("image/wu5.jpg")
det=cv2.imread("image/wu31.jpg")

print('原图和去雾图的MSE为{}'.format(MSE(src,det)))

4、后续补充 均有api

from skimage.metrics import mean_squared_error as MSE
from skimage.metrics import structural_similarity as SSIM
from skimage.metrics import peak_signal_noise_ratio as PSNR
print('原图和噪点图的MSE为{}'.format(MSE(imor,imnose)))
print('原图和噪点图的PSNR为{}'.format(SSIM(imor,imnose,multichannel=True)))
print('原图和噪点图的PSNR为{}'.format(PSNR(imor,imnose)))

见该博客