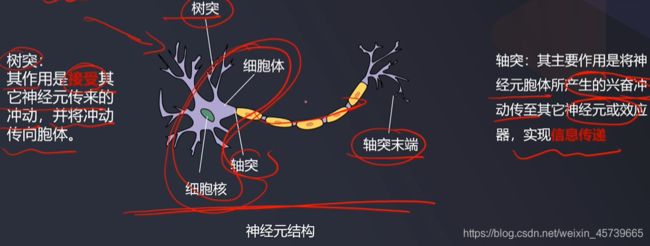
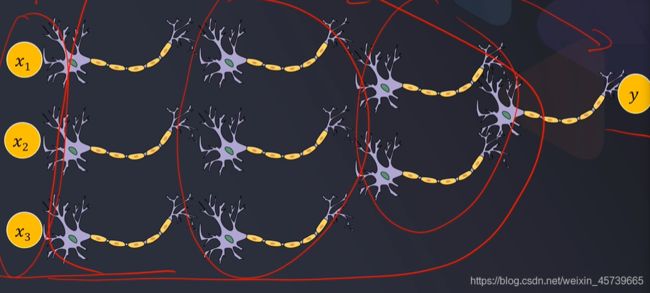
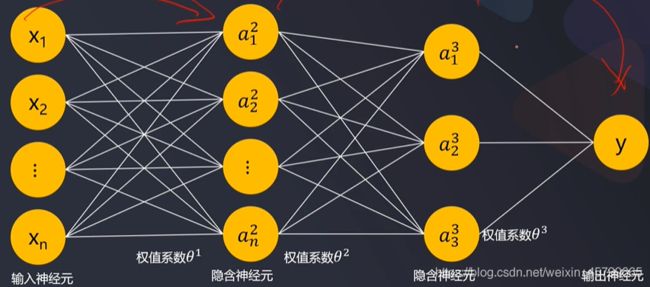
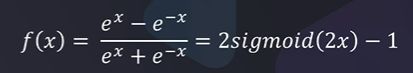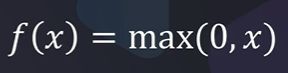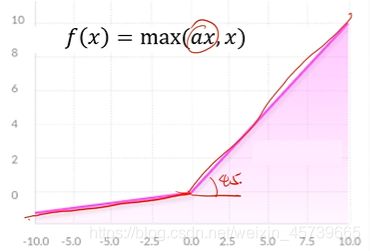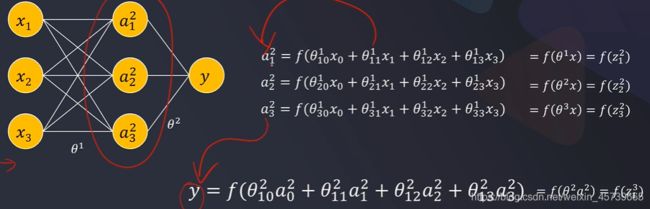深度学习之多层感知器及激活函数
目录
-
-
- 一、多层感知机MLP
-
- 1.1定义
- 二、MLP实现非线性分类
-
- 2.1MLP实现与门
- 2.2MLP实现非与门
- 2.3MLP实现或门
- 2.4MLP实现同或门
- 三、MLP实现多分类
- 四、激活函数
-
- 4.1定义
- 4.2阶跃函数
- 4.3线性函数
- 4.4Sigmoid函数
- 4.5Tanh函数
- 4.6Relu函数
- 4.7Leaky Relu函数
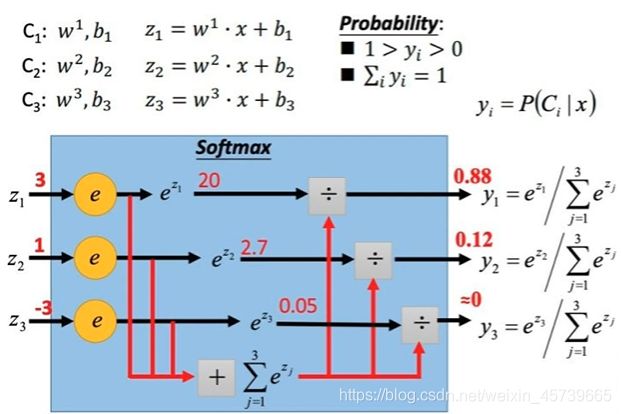
- 4.8Softmax函数
- 4.9小结:没有最好的激活函数,场景决定哪个合适
- 五、MLP的损失函数和反向算法
-
- 5.1损失函数
- 5.2多层感知器反向传播
- 六、任务
-
- 6.1MLP快速搭建非线性二分类模型
- 6.2基于数据,建立mlp模型,实现服饰图片十分类
-
一、多层感知机MLP
1.1定义
二、MLP实现非线性分类
2.1MLP实现与门
2.2MLP实现非与门
2.3MLP实现或门
2.4MLP实现同或门
三、MLP实现多分类
四、激活函数
4.1定义
4.2阶跃函数
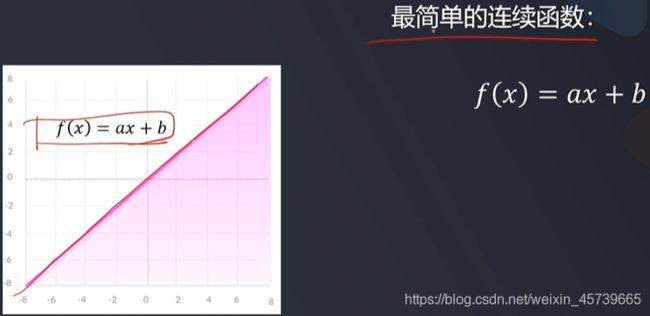
4.3线性函数
优点:
- **多个输出,而不仅仅是“是”和“不是”(1/0)
缺点:
- 无法使用梯度下降法来训练模型:导数是常数,并且与输入x无关,不利于模型求解过程中对权重的确定
- 神经网格的所有层都将折叠为线性激活关系:无论神经网络中有多少层,最后一层都是第一层的线性函数(因为线性函数的线性组合仍然是线性函数)
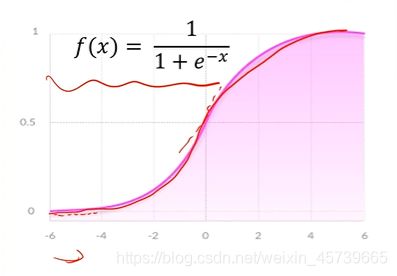
4.4Sigmoid函数
优点:
- 平滑的渐变,防止输出值跳跃
- 输出值介于0和1之间,对每个神经元的输出进行标准化
- 清晰的预测:对于大于2或小于-2的x,趋向于将y值(预测)带到曲线的边缘,非常接近1或0
缺点:
- 消失梯度:双边区域的数值饱和(x很大或很小)导致随着x变化带来的y变化很小,导数趋于零,容易造成模型求解梯度消失问题,这可能导致网络求解过程中拒绝进一步学习,或者太慢而无法获得准确的预测
- 输出y中心不是0
4.5Tanh函数
优点:
- 正负方向以原点对称,输出均值是0(与很多样本的分布均值接近),使得其收敛速度要比sigmoid快,减少迭代次数
- 具有Sigmoid函数的优点
缺点:
4.6Relu函数
优点:
- 计算效率高,允许网络快速收敛
- 非线性,尽管Relu看起来像线性函数,但它具有导数函数并允许反向传播
缺点:
4.7Leaky Relu函数
优点:
- 解决了Relu的神经元死亡问题,在负区域具有小的正斜率,因此即使对于负输入值,它也可以进行反向传播
- 具有Relu函数的优点
缺点:
- 结果不一致,无法对正负输入值提供一致的关系预测(不通过区间函数不同)
4.8Softmax函数
作用:
4.9小结:没有最好的激活函数,场景决定哪个合适
- Sigmoid、tanh:二分类任务输出层;模型隐藏层
- Relu、Leaky Relu:回归任务,卷积神经网络隐藏层
- Softmax:多分类任务输出层
五、MLP的损失函数和反向算法
5.1损失函数
5.2多层感知器反向传播
六、任务
6.1MLP快速搭建非线性二分类模型
- 基于数据,建立MLP模型,实现非线性边界二分类
- 数据分离:test_size=0.2,random_state=0
- 建模并训练模型(迭代1000次),计算训练集、测试集准确率(模型结构:一层隐藏层,25个神经元,激活函数:Sigmoid函数)
- 可视化预测结果
- 继续迭代6000次,重复步骤2-3
- 迭代1-10000次(500为间隔),查看迭代过程中的变化(可视化结果、准确率)
# In[]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family']='SimHei'
data=pd.read_csv('mlp_task1_data.csv')
# In[]
X=data.drop(['y'],axis=1)
y=data.loc[:,'y']
# In[]
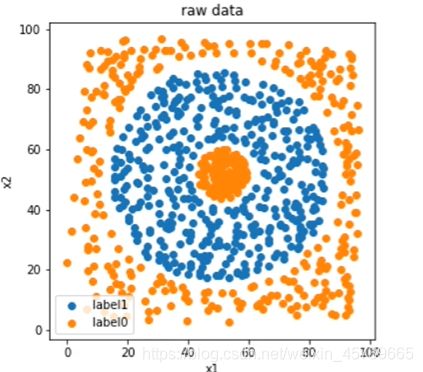
#数据可视化
fig1=plt.figure(figsize=(5,5))
plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1],label='label1')
plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0],label='lable0')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('raw data')
plt.legend()
plt.show()
# In[]
#数据分离
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
#模型建立
from keras.models import Sequential
from keras.layers import Dense,Activation
#dense:层,Activation:要使用的激活函数
#创建框架
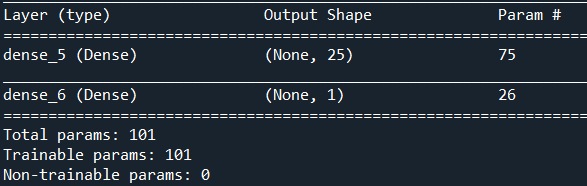
mlp=Sequential()
#创建一个有25个神经元的隐藏层(inputs_dim输入的维度)
mlp.add(Dense(units=25,input_dim=2,activation='sigmoid'))
#创建一个神经元的输出层
mlp.add(Dense(units=1,activation='sigmoid'))
mlp.summary()
#模型求解参数配置(optimiizer:求解器,loss损失函数,binary_crossentropy二分类的损失函数)
mlp.compile(optimizer='adam',loss='binary_crossentropy')
#模型训练
mlp.fit(X_train,y_train,epochs=1000)
#训练数据预测与评估
#predict_class:根据概率来给类别
y_train_predict=mlp.predict_classes(X_train)
from sklearn.metrics import accuracy_score
accuracy_train=accuracy_score(y_train,y_train_predict)
print(accuracy_train)
#测试数据预测与评估
y_test_predict=mlp.predict_classes(X_test)
accuracy_test=accuracy_score(y_test,y_test_predict)
print(accuracy_test)
#生成2D数据集
XX,yy=np.meshgrid(np.arange(0,100,1),np.arange(0,100,1))
X_range=np.c_[XX.ravel(),yy.ravel()]
print(X_range)
#生成数据结果预测
y_range_predict=mlp.predict_classes(X_range)
print(type(y_range_predict))
print(y_range_predict.shape)
#格式转化
y_range_predict_form=pd.Series(i[0] for i in y_range_predict)
print(type(y_range_predict_form))
print(y_range_predict_form)
#结果可视化
fig2=plt.figure(figsize=(5,5))
plt.scatter(X_range[:,0][y_range_predict_form==1],X_range[:,1][y_range_predict_form==1],label='label1_predict')
plt.scatter(X_range[:,0][y_range_predict_form==0],X_range[:,1][y_range_predict_form==0],label='label0_predict')
plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1],label='label1')
plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0],label='label0')
plt.title('predict_data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.show()
#逐步迭代及结果可视化
accuracy_train=[]
accuracy_test=[]
for i in range(0,21):
if i ==0:
mlp.fit(X_train,y_train,epochs=1)
else:
mlp.fit(X_train,y_train,epochs=500)
y_train_predict=mlp.predict_classes(X_train)
accuracy_train_i=accuracy_score(y_train,y_train_predict)
y_test_predict=mlp.predict_classes(X_test)
accuracy_test_i=accuracy_score(y_test,y_test_predict)
accuracy_train.append(accuracy_train_i)
accuracy_test.append(accuracy_test_i)
#生成2D数据集
xx, yy = np.meshgrid(np.arange(0,100,1),np.arange(0,100,1))
x_range = np.c_[xx.ravel(),yy.ravel()]
y_range_predict = mlp.predict_classes(x_range)
#format the output
y_range_predict_form = pd.Series(i[0] for i in y_range_predict)
fig_i = plt.figure(figsize=(5,5))
label1_predict=plt.scatter(x_range[:,0][y_range_predict_form==1],x_range[:,1][y_range_predict_form==1])
label0_predict=plt.scatter(x_range[:,0][y_range_predict_form==0],x_range[:,1][y_range_predict_form==0])
label1=plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
label0=plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
plt.legend((label1,label0,label1_predict,label0_predict),('label1','label0','label1_predict','label0_predict'))
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('epochs={}'.format(1+i*500))
plt.show()
fig_i.savefig('{}.png'.format(i),dpi=500,bbox_inches = 'tight')
# In[]
n = [1+i*500 for i in range(0,21)]
#K值变化对准确率影响的结果可视化
fig10=plt.figure(figsize=(12,5))
fig10_1=plt.subplot(121)
plt.plot(n,accuracy_train,marker='o')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.title('training data accuracy')
fig10_2=plt.subplot(122)
plt.plot(n,accuracy_test,marker='o')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.title('testing data accuracy')
plt.show()
# In[]
import imageio
def create_gif(image_list, gif_name, duration=0.35):
frames = []
for image_name in image_list:
frames.append(imageio.imread(image_name))
imageio.mimsave(gif_name, frames, 'GIF', duration=duration)
return
def main():
image_list = ['0.png','1.png','2.png','3.png','4.png','5.png','6.png','7.png','8.png','9.png','10.png','11.png','12.png','13.png','14.png','15.png','16.png','17.png','18.png','19.png','20.png']
gif_name = 'mlp.gif'
duration = 0.35
create_gif(image_list, gif_name, duration)
if __name__ == '__main__':
main()
6.2基于数据,建立mlp模型,实现服饰图片十分类
- 实现图像数据加载、可视化
- 进行数据预处理:维度转化,归一化、输出结果格式转化
- 建立mlp模型,进行模型训练与预测,计算模型在训练、测试数据集的准确率(两层隐藏层(激活函数relu),分别有392、196个神经元;输出层10类,激活函数softmax)
- 选取一个测试样本,预测其类别
- 选取测试集前10个样本,分别预测其类别
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# In[]
#图像加载与展示
from keras.datasets import fashion_mnist
(X_train,y_train),(X_test,y_test)=fashion_mnist.load_data()
print(type(X_train),'\n',X_train.shape)
# In[]
#样本可视化
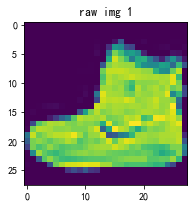
img1=X_train[0]
fig1=plt.figure(figsize=(3,3))
plt.imshow(img1)
plt.title('raw img 1')
#输入数据维度转化
feature_size=img1.shape[0]*img1.shape[1]
X_train_format=X_train.reshape(X_train.shape[0],feature_size)
X_test_format=X_test.reshape(X_test.shape[0],feature_size)
print(X_train.shape)
print(X_train_format.shape)
# In[]
#数据的归一化处理
X_train_normal=X_train_format/255
X_test_normal=X_test_format/255
print(X_train_normal[0])
# In[]
#格式化输出结果(labels)
from keras.utils import to_categorical
y_train_format=to_categorical(y_train)
y_test_format=to_categorical(y_test)
print(y_train[0])
print(y_train_format[0])
print(y_train.shape,y_train_format.shape)
#模型建立
from keras.models import Sequential
from keras.layers import Dense,Activation
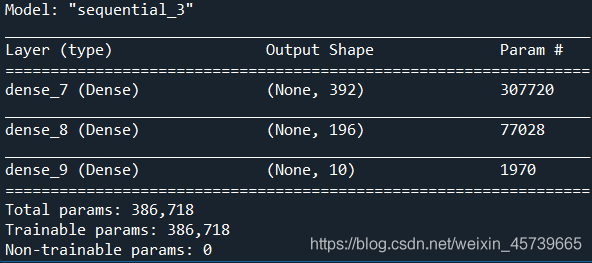
mlp=Sequential()
mlp.add(Dense(units=392,activation='relu',input_dim=784))
mlp.add(Dense(units=196,activation='relu'))
mlp.add(Dense(units=10,activation='softmax'))
mlp.summary()
#参数配置
mlp.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['categorical_accuracy'])
#多类值categorical_crossentropy,categorical_accuracy类别准确率
#模型训练
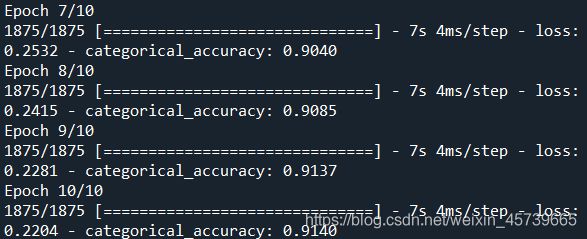
mlp.fit(X_train_normal,y_train_format,epochs=10)
#结果预测
y_train_predict=mlp.predict_classes(X_train_normal)
print(type(y_train_predict))
print(y_train_predict[0:10])
# In[]
#训练数据集预测准确率
from sklearn.metrics import accuracy_score
accuracy_train=accuracy_score(y_train,y_train_predict)
print(accuracy_train)
#测试数据集预测准确率
y_test_predict=mlp.predict_classes(X_test_normal)
accuracy_test=accuracy_score(y_test,y_test_predict)
print(accuracy_test)
#创建结果对应标签字典
label_dic={0:'T恤',1:'裤子',2:'套头衫',3:'裙子',4:'外套',5:'凉鞋',6:'衬衫',7:'运动鞋',8:'包',9:'裸靴'}
print(label_dic)
#可视化前九张图的预测结果
a=[i for i in range(1,10)]
fig4=plt.figure(figsize=(5,5))
for i in a:
plt.subplot(3,3,i)
plt.tight_layout()
plt.imshow(X_test[i])
plt.title('predict:{}'.format(label_dic[y_test_predict[i]]))
plt.xticks([])
plt.yticks([])