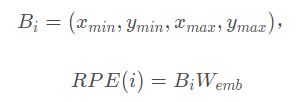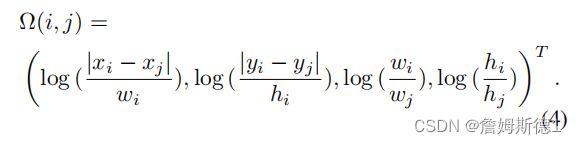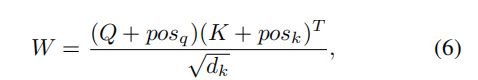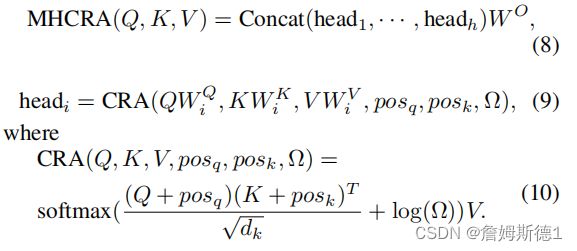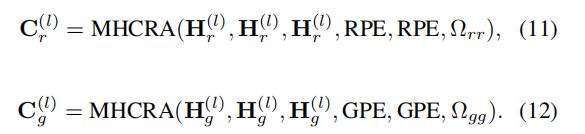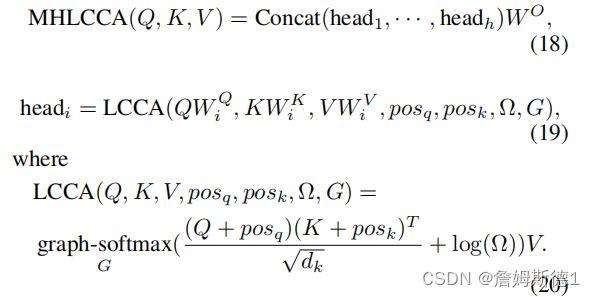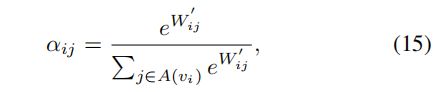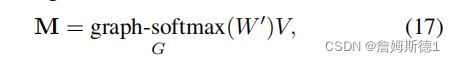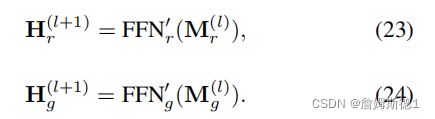论文笔记：Dual-Level Collaborative Transformer for Image Captioning
前言
论文详情可以参照这篇，写得很好。
本小白这篇内容主要是对论文中的一些思想和图以及部分公式进行自己的解读。如有错误，请多多谅解。
论文思想
首先，根据论文第一作者在知乎所说（搜这篇论文名称可以看到），自从2018年CVPR《Bottom-up and top-down attention for image captioning and visual question answering》（这篇论文的解析在这里）提出以来，image caption一直使用的是BUTD提供的Object Region特征，即第一步，先在VG上训练一个目标检测器，第二步，在COCO图片上以一定的置信度提取出图像上的目标框，第三步，将这些框中的特征作为后续（Image Captioning）模型的输入。
一般来说，为了更多覆盖全图的信息并照顾到目标比较少（甚至没有目标）的图片，这个检测的置信度会设的很低（0.2），也就是说基本上建议框都保留下来了，导致每张图片实际上有大量目标框。也有很多的冗余。
而2020CVPR《In Defense of Grid Features for Visual Question Answering》（IDGF）一文的作者发现，BUTD特征更好的原因主要是使用了VG的标注，从而给图片提供了更好的先验，通过对Detection head的改造，IDGF提取出来的grid特征在后续任务中的表现堪比甚至超过region特征。
于是作者开始思考两个特征的优缺点：
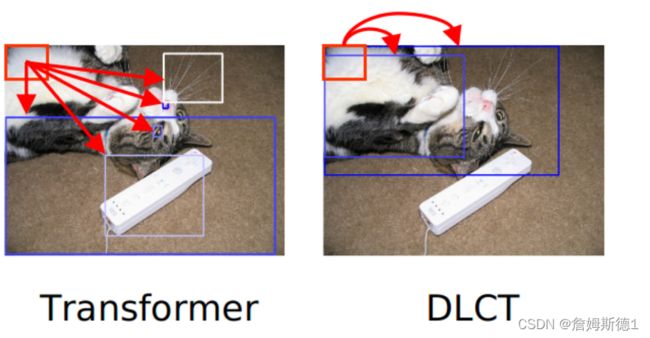
1、region特征是检测出来的目标，这些特征的语义层级相对较高，但它们有两个缺点，一是图像中非目标的区域会被忽视（如背景信息），二是大目标的小细节会被忽视。如下图所示
2、 grid特征就是Feature map，这个特征的语义层级相对较低，往往一堆网格在一起才能覆盖一个目标，但优点是它能覆盖整张图片，同时也包含了目标的细节信息。
两个特征各有优势，所以作者想把他们融合起来，这就是论文的主要思想。
论文方法
论文在摘要中写到，论文引入一种新的双层协同Transformer网络(DLCT)以实现区域和网格特征在图像描述中的互补优势。具体地说，在DLCT中，首先通过一个新的Dual-Way Self Attention(DWSA)处理两类特征源，以挖掘它们的内在属性，引入了一个综合关系注意模块(Comprehensive Relation Attention，CRA)来嵌入几何信息，此外还提出了一个位置约束交叉注意模块(Locality-Constrained Cross Attention，LCCA)来解决这两个特征直接融合引起的语义噪声，其中构造了一个几何对齐图来精确对齐和增强区域和网格特征。
论文提出了好几个东西，直接上图。
DLCT
先整体走一遍流程，首先无论是grid特征或者region特征都需要编码吧，以往的方法都是采用相对位置，本篇论文中加入了绝对位置的信息。
然后编码完了以后你相对位置和绝对位置的信息要融合吧，这就是(Comprehensive Relation Attention，CRA)。
紧接着，现在的grid特征和region特征还是两个独立的东西吧，只不过各自拥有了自己相对位置和绝对位置信息，那这两个独立的信息是不是得各自“提纯”“升华”一下，那就各自来个self-attention，这就是Dual-Way Self Attention （DWSA）
那最后，grid特征和region特征得融合了吧，如果直接丢进transformer，也就是说所有的region和grid之间都会存在信息交互，虽然前面已经“提纯”过，但有很多连接是没必要的，所以是不是得筛选一下，这就有了geometric alignment graph，几何对齐图。然后基于这个图，去掉一些“糟粕”，就可以算了吧，这就是位置约束交叉注意模块(Locality-Constrained Cross Attention，LCCA)。
整合位置信息
整合位置信息分为绝对位置编码和相对位置编码。
绝对位置编码
绝对位置编码(APE)告诉模型特征在哪里，假设有两个具有相同外观特征的物体，一个位于角落，另一个位于中心，在这种情况下，APE有助于模型准确地区分它们。对于APE，作者考虑了两种视觉特征，即网格和区域
对于网格，作者使用两个一维正弦和余弦嵌入的拼接来获得网格位置编码(GPE):
i和j是网格的行索引和列索引。
如下定义：
其中pos表示位置，k 表示维数。
对于区域，区域位置编码(RPE)中使用4维的bounding box
其中i是box的缩印，
分别表示box的左上角和右下角，W是权重矩阵。
相对位置编码
为了更好地整合视觉特征的相对位置信息，作者根据bounding boxs 的几何结构添加相对位置信息。区域的bounding box可以表示为( x , y , w , h ) ，其中x , y , w , h表示box的中心坐标及其宽度和高度。同样的，网格其实也是可以用这样的方式表示，所以对于两个不同的box之间的相对位置可以使用如下公式：
最终 
会映射为一个标量，该标量表示两个盒子之间的几何关系。
Comprehensive Relation Attention，CRA
提取出位置的绝对信息和相对信息后，就可以利用综合关系注意(Comprehensive Relation Attention, CRA)对它们进行集成。
如图所示，首先是把APE加入到queries and keys：
其中
和
分别是queries and keys的APE，然后利用相对位置信息调整注意权重：
然后就是自注意力机制那一套，softmax归一化 ：
Dual-Way Self Attention(DWSA)
这个就是“提纯”过程了，对于给定的一幅图像，我们首先提取其网格特征和区域特征，分别称为VG=
和VR=。NG和NR是对应特征的个数。然后两个独立的Self Attention模块自己做自己的。
其中，H状态是隐藏态，
分别为区域和网格的相对位置矩阵。然后对每种类型的视觉特征经过两个独立的位置前馈网络
geometric alignment graph
如上图所示，在原始的Transformer结构中，猫的白肚皮对应的grid会和各种毫无关系的object（插座、地板）进行信息交互，这种交互并没有很大的意义，而且，为了贯彻两类特征互补（高-低语义信息交互和细节信息交互）的思路，只需要几何位置上相近的特征进行交互即可，因此，论文提出了几何对齐图（Geometric Alignment Graph）。
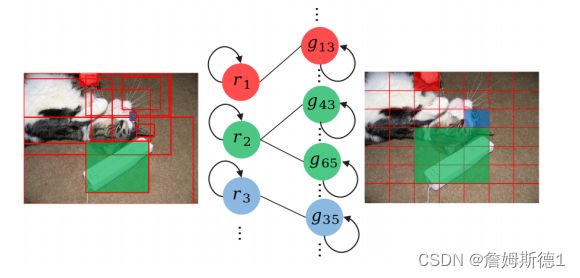
首先创建一个几何对齐图G = ( V , E ) ，所有区域和网格特征都表示为独立的节点，形成视觉节点集V。对于边集E，当且仅当网格和区域的bounding boxes有交点时，该网格节点与区域节点才相连。根据上述规则构造一个无向图，如下图所示，有交集的区域和网格(用相同颜色突出显示)由无向边缘连接，以消除语义上的不相关信息。注意每个节点都有一个自连接的边。为啥要有一个自连接的边呢？因为一个区域可以与一个或多个网格对齐，而一个网格可以与零个或多个区域对齐。可能存在一个不与区域对齐的网格。因此为几何对齐图中的每个节点创建一条自连接边。此外，自连接边给了注意力模块一个额外的选择，不关注任何其他特征。
Locality-Constrained Cross Attention(LCCA)
基于几何对齐图，我们应用LCCA来识别两种不同的视觉特征场的注意：源场和目标场。在LCCA中，源字段作为查询，而目标字段作为键和值。LCCA的目的是通过将目标场的信息嵌入到源场中来加强源场的表示。首先为了便于理解公式，我将其和前面的DWSA放在了一起比对，并且从后往前看，很显然会发现LCCA模块就是将两类特征进行了交互。其中，
是区域和网格之间的相对位置矩阵，
就是网格相对于区域的相对位置矩阵了。
通过LCCA，将区域嵌入到网格中，反之亦然，以加强两种特征。具体来说，网格特征通过区域获取高层对象信息，区域通过网格补充详细的上下文信息。LCCA利用几何对齐图约束语义不相关的视觉特征信息，消除语义噪声，有效地应用了交叉注意。
再往前看公式也是和前面类似：
既然涉及到信息交互，那自然是需要加权求和了。
vi是视觉节点，A(vi)是vi的相邻视觉节点的集合，将绝对位置信息和相对位置信息进行整合，得到权重矩阵W ′ ，并对其进行归一化
其中，Vj为第j个视觉节点值。为简单起见，我们表示这个阶段表示如下：
最后，在第L层中，注意模块后面是两个独立的FFN，就像在DWSA中一样
值得注意的是，整个encoder模块不止一层，它像transformer一样有N层，所以，LCCA的输出作为DWSA的输入。经过多层编码后，网格特征和区域特征被连接并输入解码器层。
总结
实验部分有兴趣的可以去阅读原文，这里就不做过多阐述。
这篇论文作者提出了一种新的双层协同Transformer网络(DLCT)，实现了区域特征和网格特征的互补性。提出了位置约束交叉注意(LCCA)来解决两个特征源直接融合引起的语义噪声问题。在几何对齐图的帮助下，两类特征之间的交互变得更加高效，也更加符合最初的动机，也带来了性能的提升。论文尝试探索图像描述的绝对位置信息。通过集成绝对位置信息和相对位置信息在一开始的编码上就让模型获取更多的位置信息。