如何评价2022年数维杯国际赛C题【如何使用大脑结构诊断阿尔茨海默病】【D题：拉尼娜事件】思路模型代码全套资料+高清代码结果图+完整源程序+论文

资料获取方式我放到下面了，欢迎小伙伴一起学习交流

2022数维杯国际赛C题：https://mbd.pub/o/bread/Y5yVlp1x

2022年数维杯国际赛【D题：拉尼娜事件】思路模型代码全套资料！全网最全，更新完毕......
所有的参考代码含高清运行结果图+LITM神经网络参考代码+D题思路全部(50页参考论文）https://mbd.pub/o/bread/Y5yVl5dr

 

大家好呀，数维杯国际赛早上8点开始了，拿到赛题之后我也在第一时间研究，现在先给大家一个初步的选题建议及C题的初步思路。欢迎小伙伴一起交流
首先是选题建议：
AB题目。也就是mcm类型的，理论方面难度较大，只建议有相关专业知识或者数理基础扎实编程能力强的队伍去选择。
CD题目，icm类，比较好上手，小白队伍推荐选择，并且，更建议C题，我也会首先做C题，做完c之后再决定做不做D。
为什么更建议C题？因为题目数据已经给出，并且目标明确。
而D题，在第一步搜寻有效数据以及确定有效指标方面就已经能卡壳一大堆队伍了。
OK那么废话不多说，首先说一下C题我自己的初步思路，注意，只是初步思路，我目前正在解题以及撰写完整的论文，预计今晚到明早完成，实际解题过程中，我会不断调整优化思路，大家点赞关注收藏一下，后续我也会在这里继续更新，
需要完整成品的，看我主页简介即可。
题目背景就不多说了
对于c题，本质上解题思路上，难度不大，重点在于数据分析的计算量比较大。

 

请大家务必认准原创！我从不跟任何其他资料沾边，任何东西都是我个人原创作品！！！

好了，正文开始，从昨天早上发布题目到现在，一直在肝c题，现在终于完成。这里是图文的解答，稍后我会录制详细的讲解视频，b站同名账号首发。

总体而言，本题做得还是比较顺的，就只是数据多了点，分类我用决策树准确率90％多，没什么毛病，聚类相关性这些就不用说了，无脑操作就完事，本题重点还是在于特征筛选以及理解题意上。

而我最终的成品一共51页：

目前唯一获取方式是这个在线文档：2022数维杯完整成品参考

之所以篇幅这么长，是因为

1.我论文很多的篇幅需要用来解释我为什么要这么做，基本就是手把手教你怎么做，并且我还要照顾每个人的水平，所有会有些地方需要写得很繁琐，一些中间过程展现得事无巨细，需要你们自己删减到25页左右。

2.本题难度不算大，但特征确实多，光第一问我筛除了缺失值较多的特征之后都还有42个特征，之后相关性较强的竟然还是有11个，这也导致后续分析中，所有的表格都很大，但是没办法，特征必须要写全。

OK，我的

摘要：

第一问：

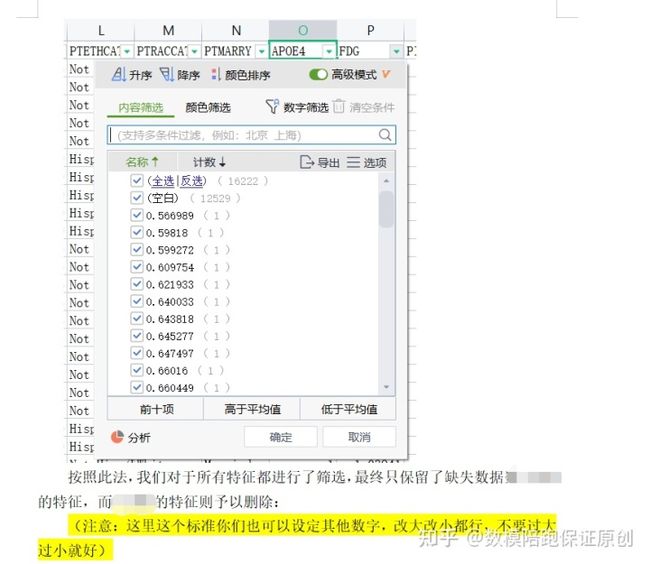
预处理嘛，这么多特征，肯定要首先对于特征进行筛选，把那些缺失值比较多的筛选掉，直接看空白值有多少就行了：

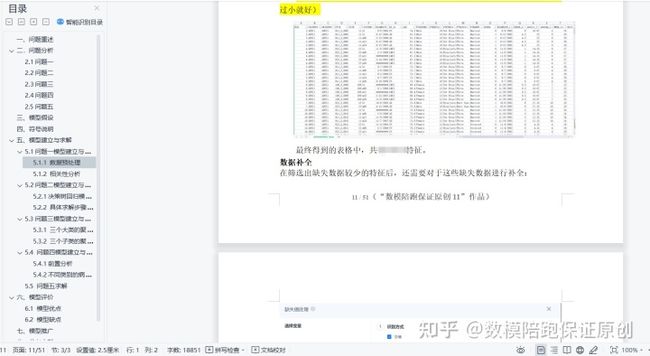
把空白值多的全删了，得到最终表格：

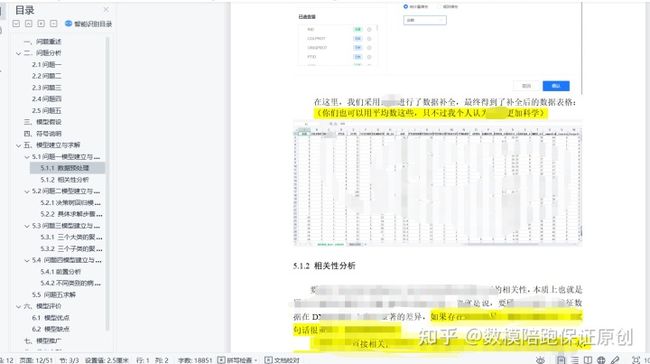
之后，虽然剩下的特征空白值比较少，但是还是要补全：

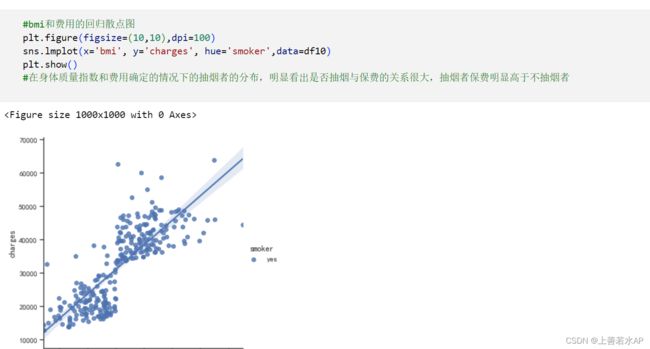
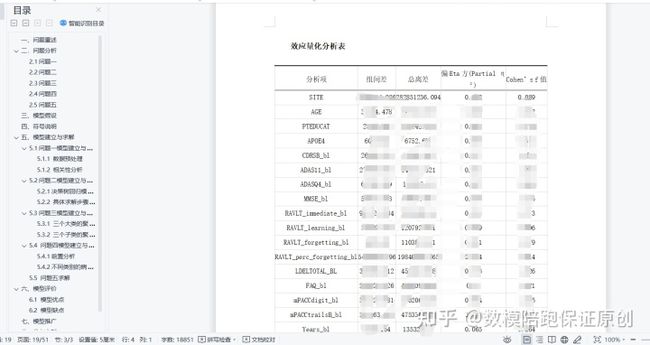
ok，之后就是要做相关性分析了，这里由于需要对于是否患病这个类变量进行相关性分析，那么直接用热力图是不合适的，由此，我修正了之前的思路，改用了方差分析：

其实就是看谁差异大，谁差异大谁自然相关性强。

最终得到方差图和表格：

根据表格，然后看谁的值大就完事了：

最终获得了11个相关性比较大的，ok第一问完事。

第二问：

识别模型嘛，无脑机器学习就完事了，没什么可以考虑的。

机器学习采用的训练集数据，自然是第一问得出的相关性比较大的这些特征的数据，相关性不大凭什么用来判别？

然后我直接决策树回归吧，本来用的svm，但是svm确实不适用于大数据哈，识别精度60%多，舍弃。

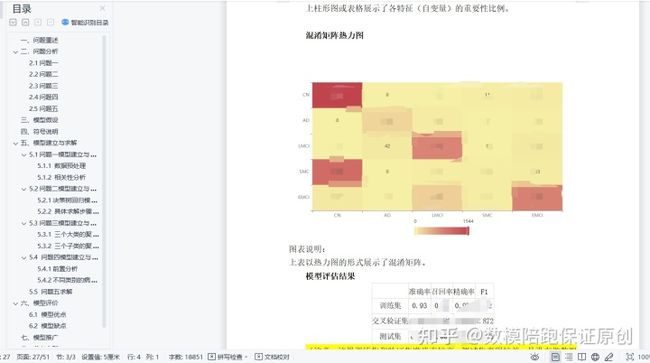
得到最后的识别精度：

优化了很多遍参数，最后我划分的训练集的准确率，93%，够可以了，我也就不用再优化了。

OK第二问结束。

太累了还要忙着做D题，后面我就写得笼统一点了。。。。

第三问：

无脑kmeans聚类分析就完事了，重点只是理解题意，究竟要怎么去聚类，聚类哪些数据。。。

第四问：

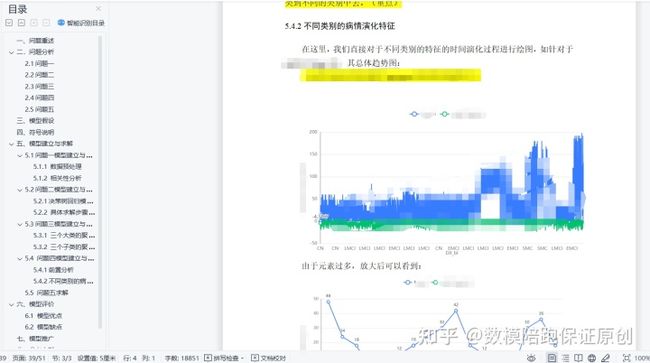
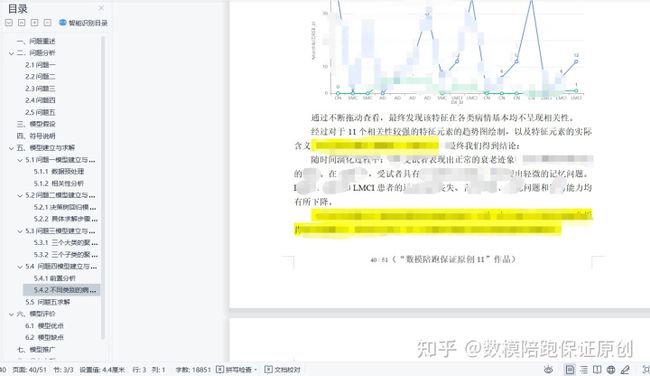
绘图看一下演变趋势罢了，简单到不用思考，重点只是在于这么多数据怎么绘图以及怎么分析这个趋势：

第五问：

这是最不用多说的一问了，查文献而已，谁都会，只要保证自己查到的足够全面即可。

OK，暂时就是这些了，以上全文的获取在在线文档：

2022数维杯

最后再给点附录代码大家做参考吧，只给个聚类的好了：

function [Idx, Center] = K_means(X, xstart)
% K-means聚类
% Idx是数据点属于哪个类的标记，Center是每个类的中心位置
% X是全部二维数据点，xstart是类的初始中心位置

len = length(X);        %X中的数据点个数
Idx = zeros(len, 1);    %每个数据点的Id，即属于哪个类

C1 = xstart(1,:);       %第1类的中心位置
C2 = xstart(2,:);       %第2类的中心位置
C3 = xstart(3,:);       %第3类的中心位置

for i_for = 1:100
    %为避免循环运行时间过长，通常设置一个循环次数
    %或相邻两次聚类中心位置调整幅度小于某阈值则停止
    
    %更新数据点属于哪个类
    for i = 1:len
        x_temp = X(i,:);    %提取出单个数据点
        d1 = norm(x_temp - C1);    %与第1个类的距离
        d2 = norm(x_temp - C2);    %与第2个类的距离
        d3 = norm(x_temp - C3);    %与第3个类的距离
        d = [d1;d2;d3];
        [~, id] = min(d);   %离哪个类最近则属于那个类
        Idx(i) = id;
    end
    
    %更新类的中心位置
    L1 = X(Idx == 1,:);     %属于第1类的数据点
    L2 = X(Idx == 2,:);     %属于第2类的数据点
    L3 = X(Idx == 3,:);     %属于第3类的数据点
    C1 = mean(L1);      %更新第1类的中心位置
    C2 = mean(L2);      %更新第2类的中心位置
    C3 = mean(L3);      %更新第3类的中心位置
end

Center = [C1; C2; C3];  %类的中心位置